Complete Reference for Bitwise Operators in Programming/Coding
Last Updated :
28 Dec, 2023
There exists no programming language that doesn't use Bit Manipulations. Bit manipulation is all about these bitwise operations. They improve the efficiency of programs by being primitive, fast actions. There are different bitwise operations used in bit manipulation. These Bitwise Operators operate on the individual bits of the bit patterns. Bit operations are fast and can be used in optimizing time complexity.
Some common bit operators are:
 Bitwise Operator Truth Table
Bitwise Operator Truth Table1. Bitwise AND Operator (&)
The bitwise AND operator is denoted using a single ampersand symbol, i.e. &. The & operator takes two equal-length bit patterns as parameters. The two-bit integers are compared. If the bits in the compared positions of the bit patterns are 1, then the resulting bit is 1. If not, it is 0.
 Truth table of AND operator
Truth table of AND operatorExample:
Take two bit values X and Y, where X = 7= (111)2 and Y = 4 = (100)2 . Take Bitwise and of both X & y
 Bitwise ANDof (7 & 4)
Bitwise ANDof (7 & 4)
Implementation of AND operator:
C++
#include <bits/stdc++.h>
using namespace std;
int main()
{
int a = 7, b = 4;
int result = a & b;
cout << result << endl;
return 0;
}
/*package whatever //do not write package name here */
import java.io.*;
class GFG {
public static void main (String[] args) {
int a = 7, b = 4;
int result = a & b;
System.out.println(result);
}
}
// This code is contributed by lokeshmvs21.
a = 7
b = 4
result = a & b
print(result)
# This code is contributed by akashish__
using System;
public class GFG{
static public void Main (){
int a = 7, b = 4;
int result = a & b;
Console.WriteLine(result);
}
}
// This code is contributed by akashish__
let a = 7, b = 4;
let result = a & b;
console.log(result);
// This code is contributed by akashish__
Time Complexity: O(1)
Auxiliary Space: O(1)
2. Bitwise OR Operator (|)
The | Operator takes two equivalent length bit designs as boundaries; if the two bits in the looked-at position are 0, the next bit is zero. If not, it is 1.
.png)
Example:
Take two bit values X and Y, where X = 7= (111)2 and Y = 4 = (100)2 . Take Bitwise OR of both X, y
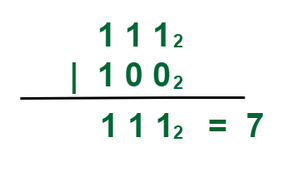 Bitwise OR of (7 | 4)
Bitwise OR of (7 | 4)Explanation: On the basis of truth table of bitwise OR operator we can conclude that the result of
1 | 1 = 1
1 | 0 = 1
0 | 1 = 1
0 | 0 = 0
We used the similar concept of bitwise operator that are show in the image.
Implementation of OR operator:
C++
#include <bits/stdc++.h>
using namespace std;
int main()
{
int a = 12, b = 25;
int result = a | b;
cout << result;
return 0;
}
import java.io.*;
class GFG {
public static void main(String[] args)
{
int a = 12, b = 25;
int result = a | b;
System.out.println(result);
}
}
a = 12
b = 25
result = a | b
print(result)
# This code is contributed by garg28harsh.
using System;
public class GFG{
static public void Main (){
int a = 12, b = 25;
int result = a | b;
Console.WriteLine(result);
}
}
// This code is contributed by akashish__
let a = 12, b = 25;
let result = a | b;
document.write(result);
// This code is contributed by garg28harsh.
Time Complexity: O(1)
Auxiliary Space: O(1)
3. Bitwise XOR Operator (^)
The ^ operator (also known as the XOR operator) stands for Exclusive Or. Here, if bits in the compared position do not match their resulting bit is 1. i.e, The result of the bitwise XOR operator is 1 if the corresponding bits of two operands are opposite, otherwise 0.
.png)
Example:
Take two bit values X and Y, where X = 7= (111)2 and Y = 4 = (100)2 . Take Bitwise and of both X & y
 Bitwise OR of (7 ^ 4)
Bitwise OR of (7 ^ 4)Explanation: On the basis of truth table of bitwise XOR operator we can conclude that the result of
1 ^ 1 = 0
1 ^ 0 = 1
0 ^ 1 = 1
0 ^ 0 = 0
We used the similar concept of bitwise operator that are show in the image.
Implementation of XOR operator:
C++
#include <iostream>
using namespace std;
int main()
{
int a = 12, b = 25;
cout << (a ^ b);
return 0;
}
import java.io.*;
class GFG {
public static void main(String[] args)
{
int a = 12, b = 25;
int result = a ^ b;
System.out.println(result);
}
}
// This code is contributed by garg28harsh.
a = 12
b = 25
result = a ^ b
print(result)
# This code is contributed by garg28harsh.
// C# Code
using System;
public class GFG {
static public void Main()
{
// Code
int a = 12, b = 25;
int result = a ^ b;
Console.WriteLine(result);
}
}
// This code is contributed by lokesh
let a = 12;
let b = 25;
console.log((a ^ b));
// This code is contributed by akashish__
Time Complexity: O(1)
Auxiliary Space: O(1)
4. Bitwise NOT Operator (!~)
All the above three bitwise operators are binary operators (i.e, requiring two operands in order to operate). Unlike other bitwise operators, this one requires only one operand to operate.
The bitwise Not Operator takes a single value and returns its one’s complement. The one’s complement of a binary number is obtained by toggling all bits in it, i.e, transforming the 0 bit to 1 and the 1 bit to 0.
 Truth Table of Bitwise Operator NOT
Truth Table of Bitwise Operator NOTExample:
Take two bit values X and Y, where X = 5= (101)2 . Take Bitwise NOT of X.

Explanation: On the basis of truth table of bitwise NOT operator we can conclude that the result of
~1 = 0
~0 = 1
We used the similar concept of bitwise operator that are show in the image.
Implementation of NOT operator:
C++
#include <iostream>
using namespace std;
int main()
{
int a = 0;
cout << "Value of a without using NOT operator: " << a;
cout << "\nInverting using NOT operator (with sign bit): " << (~a);
cout << "\nInverting using NOT operator (without sign bit): " << (!a);
return 0;
}
/*package whatever //do not write package name here */
import java.io.*;
class GFG {
public static void main(String[] args)
{
int a = 0;
System.out.println(
"Value of a without using NOT operator: " + a);
System.out.println(
"Inverting using NOT operator (with sign bit): "
+ (~a));
if (a != 1)
System.out.println(
"Inverting using NOT operator (without sign bit): 1");
else
System.out.println(
"Inverting using NOT operator (without sign bit): 0");
}
}
// This code is contributed by lokesh.
a = 0
print("Value of a without using NOT operator: " , a)
print("Inverting using NOT operator (with sign bit): " , (~a))
print("Inverting using NOT operator (without sign bit): " , int(not(a)))
# This code is contributed by akashish__
using System;
public class GFG {
static public void Main()
{
int a = 0;
Console.WriteLine(
"Value of a without using NOT operator: " + a);
Console.WriteLine(
"Inverting using NOT operator (with sign bit): "
+ (~a));
if (a != 1)
Console.WriteLine(
"Inverting using NOT operator (without sign bit): 1");
else
Console.WriteLine(
"Inverting using NOT operator (without sign bit): 0");
}
}
// This code is contributed by akashish__
let a =0;
document.write("Value of a without using NOT operator: " + a);
document.write( "Inverting using NOT operator (with sign bit): " + (~a));
if(!a)
document.write( "Inverting using NOT operator (without sign bit): 1" );
else
document.write( "Inverting using NOT operator (without sign bit): 0" );
OutputValue of a without using NOT operator: 0
Inverting using NOT operator (with sign bit): -1
Inverting using NOT operator (without sign bit): 1
Time Complexity: O(1)
Auxiliary Space: O(1)
5. Left-Shift (<<)
The left shift operator is denoted by the double left arrow key (<<). The general syntax for left shift is shift-expression << k. The left-shift operator causes the bits in shift expression to be shifted to the left by the number of positions specified by k. The bit positions that the shift operation has vacated are zero-filled.
Note: Every time we shift a number towards the left by 1 bit it multiply that number by 2.
 Logical left Shift
Logical left ShiftExample:
Input: Left shift of 5 by 1.
Binary representation of 5 = 00101 and Left shift of 001012 by 1 (i.e, 00101 << 1)
 Left shift of 5 by 1
Left shift of 5 by 1Output: 10
Explanation: All bit of 5 will be shifted by 1 to left side and this result in 010102, Which is equivalent to 10
Input: Left shift of 5 by 2.
Binary representation of 5 = 00101 and Left shift of 001012 by 1 (i.e, 00101 << 2)
 Left shift of 5 by 2
Left shift of 5 by 2Output: 20
Explanation: All bit of 5 will be shifted by 1 to left side and this result in 101002, Which is equivalent to 20
Input: Left shift of 5 by 3.
Binary representation of 5 = 00101 and Left shift of 001012 by 1 (i.e, 00101 << 3)
 Left shift of 5 by 3
Left shift of 5 by 3Output: 40
Explanation: All bit of 5 will be shifted by 1 to left side and this result in 010002, Which is equivalent to 40
Implementation of Left shift operator:
C++
#include <bits/stdc++.h>
using namespace std;
int main()
{
unsigned int num1 = 1024;
bitset<32> bt1(num1);
cout << bt1 << endl;
unsigned int num2 = num1 << 1;
bitset<32> bt2(num2);
cout << bt2 << endl;
unsigned int num3 = num1 << 2;
bitset<16> bitset13{ num3 };
cout << bitset13 << endl;
}
/*package whatever //do not write package name here */
import java.io.*;
class GFG {
public static void main(String[] args)
{
int num1 = 1024;
String bt1 = Integer.toBinaryString(num1);
bt1 = String.format("%32s", bt1).replace(' ', '0');
System.out.println(bt1);
int num2 = num1 << 1;
String bt2 = Integer.toBinaryString(num2);
bt2 = String.format("%32s", bt2).replace(' ', '0');
System.out.println(bt2);
int num3 = num1 << 2;
String bitset13 = Integer.toBinaryString(num3);
bitset13 = String.format("%16s", bitset13)
.replace(' ', '0');
System.out.println(bitset13);
}
}
// This code is contributed by akashish__
# Python code for the above approach
num1 = 1024
bt1 = bin(num1)[2:].zfill(32)
print(bt1)
num2 = num1 << 1
bt2 = bin(num2)[2:].zfill(32)
print(bt2)
num3 = num1 << 2
bitset13 = bin(num3)[2:].zfill(16)
print(bitset13)
# This code is contributed by Prince Kumar
using System;
class GFG {
public static void Main(string[] args)
{
int num1 = 1024;
string bt1 = Convert.ToString(num1, 2);
bt1 = bt1.PadLeft(32, '0');
Console.WriteLine(bt1);
int num2 = num1 << 1;
string bt2 = Convert.ToString(num2, 2);
bt2 = bt2.PadLeft(32, '0');
Console.WriteLine(bt2);
int num3 = num1 << 2;
string bitset13 = Convert.ToString(num3, 2);
bitset13 = bitset13.PadLeft(16, '0');
Console.WriteLine(bitset13);
}
}
// This code is contributed by akashish__
// JavaScript code for the above approach
let num1 = 1024;
let bt1 = num1.toString(2).padStart(32, '0');
console.log(bt1);
let num2 = num1 << 1;
let bt2 = num2.toString(2).padStart(32, '0');
console.log(bt2);
let num3 = num1 << 2;
let bitset13 = num3.toString(2).padStart(16, '0');
console.log(bitset13);
Output00000000000000000000010000000000
00000000000000000000100000000000
0001000000000000
Time Complexity: O(1)
Auxiliary Space: O(1)
6. Right-Shift (>>)
The right shift operator is denoted by the double right arrow key (>>). The general syntax for the right shift is "shift-expression >> k". The right-shift operator causes the bits in shift expression to be shifted to the right by the number of positions specified by k. For unsigned numbers, the bit positions that the shift operation has vacated are zero-filled. For signed numbers, the sign bit is used to fill the vacated bit positions. In other words, if the number is positive, 0 is used, and if the number is negative, 1 is used.
Note: Every time we shift a number towards the right by 1 bit it divides that number by 2.
 Logical Right Shift
Logical Right ShiftExample:
Input: Left shift of 5 by 1.
Binary representation of 5 = 00101 and Left shift of 001012 by 1 (i.e, 00101 << 1)
 Right shift of 5 by 1
Right shift of 5 by 1Output: 10
Explanation: All bit of 5 will be shifted by 1 to left side and this result in 010102, Which is equivalent to 10
Input: Left shift of 5 by 2.
Binary representation of 5 = 00101 and Left shift of 001012 by 1 (i.e, 00101 << 2)
 Right shift of 5 by 2
Right shift of 5 by 2Output: 20
Explanation: All bit of 5 will be shifted by 1 to left side and this result in 101002, Which is equivalent to 20
Input: Left shift of 5 by 3.
Binary representation of 5 = 00101 and Left shift of 001012 by 1 (i.e, 00101 << 3)
 Right shift of 5 by 3
Right shift of 5 by 3Output: 40
Explanation: All bit of 5 will be shifted by 1 to left side and this result in 010002, Which is equivalent to 40
Implementation of Right shift operator:
C++
#include <bitset>
#include <iostream>
using namespace std;
int main()
{
unsigned int num1 = 1024;
bitset<32> bt1(num1);
cout << bt1 << endl;
unsigned int num2 = num1 >> 1;
bitset<32> bt2(num2);
cout << bt2 << endl;
unsigned int num3 = num1 >> 2;
bitset<16> bitset13{ num3 };
cout << bitset13 << endl;
}
// Java code for the above approach
class GFG {
public static void main(String[] args)
{
int num1 = 1024;
String bt1
= String
.format("%32s",
Integer.toBinaryString(num1))
.replace(' ', '0');
System.out.println(bt1);
int num2 = num1 >> 1;
String bt2
= String
.format("%32s",
Integer.toBinaryString(num2))
.replace(' ', '0');
System.out.println(bt2);
int num3 = num1 >> 2;
String bitset13
= String
.format("%16s",
Integer.toBinaryString(num3))
.replace(' ', '0');
System.out.println(bitset13);
}
}
// This code is contributed by ragul21
num1 = 1024
bt1 = bin(num1)[2:].zfill(32)
print(bt1)
num2 = num1 >> 1
bt2 = bin(num2)[2:].zfill(32)
print(bt2)
num3 = num1 >> 2
bitset13 = bin(num3)[2:].zfill(16)
print(bitset13)
using System;
class Program
{
static void Main()
{
int num1 = 1024;
// Right shift by 1
int num2 = num1 >> 1;
// Right shift by 2
int num3 = num1 >> 2;
// Print binary representations
string bt1 = Convert.ToString(num1, 2).PadLeft(32, '0');
string bt2 = Convert.ToString(num2, 2).PadLeft(32, '0');
string bitset13 = Convert.ToString(num3, 2).PadLeft(16, '0');
Console.WriteLine(bt1);
Console.WriteLine(bt2);
Console.WriteLine(bitset13);
}
}
// JavaScript code for the above approach
let num1 = 1024;
let bt1 = num1.toString(2).padStart(32, '0');
console.log(bt1);
let num2 = num1 >> 1;
let bt2 = num2.toString(2).padStart(32, '0');
console.log(bt2);
let num3 = num1 >> 2;
let bitset13 = num3.toString(2).padStart(16, '0');
console.log(bitset13);
// akashish__
Output00000000000000000000010000000000
00000000000000000000001000000000
0000000100000000
Time Complexity: O(1)
Auxiliary Space: O(1)
Application of BIT Operators
- Bit operations are used for the optimization of embedded systems.
- The Exclusive-or operator can be used to confirm the integrity of a file, making sure it has not been corrupted, especially after it has been in transit.
- Bitwise operations are used in Data encryption and compression.
- Bits are used in the area of networking, framing the packets of numerous bits which are sent to another system generally through any type of serial interface.
- Digital Image Processors use bitwise operations to enhance image pixels and to extract different sections of a microscopic image.
Similar Reads
DSA Tutorial - Learn Data Structures and Algorithms DSA (Data Structures and Algorithms) is the study of organizing data efficiently using data structures like arrays, stacks, and trees, paired with step-by-step procedures (or algorithms) to solve problems effectively. Data structures manage how data is stored and accessed, while algorithms focus on
7 min read
Quick Sort QuickSort is a sorting algorithm based on the Divide and Conquer that picks an element as a pivot and partitions the given array around the picked pivot by placing the pivot in its correct position in the sorted array. It works on the principle of divide and conquer, breaking down the problem into s
12 min read
Merge Sort - Data Structure and Algorithms Tutorials Merge sort is a popular sorting algorithm known for its efficiency and stability. It follows the divide-and-conquer approach. It works by recursively dividing the input array into two halves, recursively sorting the two halves and finally merging them back together to obtain the sorted array. Merge
14 min read
Data Structures Tutorial Data structures are the fundamental building blocks of computer programming. They define how data is organized, stored, and manipulated within a program. Understanding data structures is very important for developing efficient and effective algorithms. What is Data Structure?A data structure is a st
2 min read
Bubble Sort Algorithm Bubble Sort is the simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in the wrong order. This algorithm is not suitable for large data sets as its average and worst-case time complexity are quite high.We sort the array using multiple passes. After the fir
8 min read
Breadth First Search or BFS for a Graph Given a undirected graph represented by an adjacency list adj, where each adj[i] represents the list of vertices connected to vertex i. Perform a Breadth First Search (BFS) traversal starting from vertex 0, visiting vertices from left to right according to the adjacency list, and return a list conta
15+ min read
Binary Search Algorithm - Iterative and Recursive Implementation Binary Search Algorithm is a searching algorithm used in a sorted array by repeatedly dividing the search interval in half. The idea of binary search is to use the information that the array is sorted and reduce the time complexity to O(log N). Binary Search AlgorithmConditions to apply Binary Searc
15 min read
Insertion Sort Algorithm Insertion sort is a simple sorting algorithm that works by iteratively inserting each element of an unsorted list into its correct position in a sorted portion of the list. It is like sorting playing cards in your hands. You split the cards into two groups: the sorted cards and the unsorted cards. T
9 min read
Array Data Structure Guide In this article, we introduce array, implementation in different popular languages, its basic operations and commonly seen problems / interview questions. An array stores items (in case of C/C++ and Java Primitive Arrays) or their references (in case of Python, JS, Java Non-Primitive) at contiguous
4 min read
Sorting Algorithms A Sorting Algorithm is used to rearrange a given array or list of elements in an order. For example, a given array [10, 20, 5, 2] becomes [2, 5, 10, 20] after sorting in increasing order and becomes [20, 10, 5, 2] after sorting in decreasing order. There exist different sorting algorithms for differ
3 min read