Modify a binary tree to get preorder traversal using right pointers only
Last Updated :
29 Oct, 2024
Given a binary tree. The task is to modify it in such a way that after modification preorder traversal of it can get only with the right pointers. During modification, we can use right as well as left pointers.
Examples:
Input :

Output :
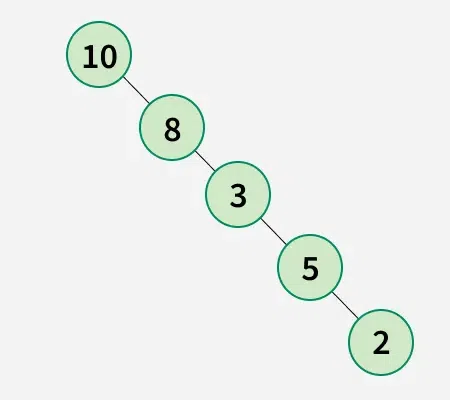
Explanation: The preorder traversal of given binary tree is 10 8 3 5 2.
[Expected Approach - 1] Using recursion - O(n) Time and O(h) Space
The idea is to use recursion to transform the tree, the right pointer of the root is made to point to the left subtree. If the node has only a left child, the left child is moved to the right, completing the processing for that node. However, if the node has both left and right children, the original right child is moved to the rightmost node of the left subtree. This process ensures that the entire left subtree is shifted to the right, and the rightmost node of the transformed subtree is returned after the node is processed.
Below is the implementation of the above approach:
C++
// C++ code to modify binary tree for
// traversal using only right pointer
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int data;
Node* left;
Node* right;
Node(int x){
data = x;
left = right = nullptr;
}
};
// Function to modify tree
Node* modifytree(Node* root) {
Node* right = root->right;
Node* rightMost = root;
// if the left tree exists
if (root->left) {
// get the right-most of the
// original left subtree
rightMost = modifytree(root->left);
// set root right to left subtree
root->right = root->left;
root->left = nullptr;
}
// if the right subtree does
// not exists we are done!
if (!right)
return rightMost;
// set right pointer of right-most
// of the original left subtree
rightMost->right = right;
// modify the rightsubtree
rightMost = modifytree(right);
return rightMost;
}
void printpre(Node* curr) {
while (curr != nullptr) {
cout << curr->data << " ";
curr = curr->right;
}
}
int main() {
// Constructed binary tree is
// 10
// / \
// 8 2
// / \
// 3 5
Node* root = new Node(10);
root->left = new Node(8);
root->right = new Node(2);
root->left->left = new Node(3);
root->left->right = new Node(5);
modifytree(root);
printpre(root);
return 0;
}
// Java code to modify binary tree for traversal
// using only right pointer
class Node {
int data;
Node left, right;
public Node(int x) {
data = x;
left = right = null;
}
}
class GfG {
// Function to modify tree
static Node modifytree(Node root) {
Node right = root.right;
Node rightMost = root;
// If the left tree exists
if (root.left != null) {
// Get the right-most of the original left
// subtree
rightMost = modifytree(root.left);
// Set root right to left subtree
root.right = root.left;
root.left = null;
}
// If the right subtree does not
// exist we are done!
if (right == null)
return rightMost;
// Set right pointer of right-most of the original
// left subtree
rightMost.right = right;
// Modify the right subtree
rightMost = modifytree(right);
return rightMost;
}
static void printpre(Node curr) {
while (curr != null) {
System.out.print(curr.data + " ");
curr = curr.right;
}
}
public static void main(String[] args) {
// Constructed binary tree is
// 10
// / \
// 8 2
// / \
// 3 5
Node root = new Node(10);
root.left = new Node(8);
root.right = new Node(2);
root.left.left = new Node(3);
root.left.right = new Node(5);
modifytree(root);
printpre(root);
}
}
# Python code to modify binary tree for traversal using
# only right pointer
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
# Function to modify tree
def modifytree(root):
right = root.right
right_most = root
# If the left tree exists
if root.left:
# Get the right-most of the original
# left subtree
right_most = modifytree(root.left)
# Set root right to left subtree
root.right = root.left
root.left = None
# If the right subtree does not exist
# we are done!
if not right:
return right_most
# Set right pointer of right-most of the
# original left subtree
right_most.right = right
# Modify the right subtree
right_most = modifytree(right)
return right_most
def printpre(curr):
while curr:
print(curr.data, end=" ")
curr = curr.right
if __name__ == "__main__":
# Constructed binary tree is
# 10
# / \
# 8 2
# / \
# 3 5
root = Node(10)
root.left = Node(8)
root.right = Node(2)
root.left.left = Node(3)
root.left.right = Node(5)
modifytree(root)
printpre(root)
// C# code to modify binary tree for traversal using only
// right pointer
using System;
class Node {
public int data;
public Node left, right;
public Node(int x) {
data = x;
left = right = null;
}
}
class GfG {
// Function to modify tree
static Node modifytree(Node root) {
Node right = root.right;
Node rightMost = root;
// If the left tree exists
if (root.left != null) {
// Get the right-most of the original left
// subtree
rightMost = modifytree(root.left);
// Set root right to left subtree
root.right = root.left;
root.left = null;
}
// If the right subtree does
// not exist we are done!
if (right == null)
return rightMost;
// Set right pointer of right-most of the original
// left subtree
rightMost.right = right;
// Modify the right subtree
rightMost = modifytree(right);
return rightMost;
}
static void printpre(Node curr) {
while (curr != null) {
Console.Write(curr.data + " ");
curr = curr.right;
}
}
static void Main(string[] args) {
// Constructed binary tree is
// 10
// / \
// 8 2
// / \
// 3 5
Node root = new Node(10);
root.left = new Node(8);
root.right = new Node(2);
root.left.left = new Node(3);
root.left.right = new Node(5);
modifytree(root);
printpre(root);
}
}
// JavaScript code to modify binary tree for traversal using
// only right pointer
class Node {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
}
// Function to modify tree
function modifytree(root) {
let right = root.right;
let rightMost = root;
// If the left tree exists
if (root.left) {
// Get the right-most of the original
// left subtree
rightMost = modifytree(root.left);
// Set root right to left subtree
root.right = root.left;
root.left = null;
}
// If the right subtree does not
// exist we are done!
if (!right)
return rightMost;
// Set right pointer of right-most of
//the original left subtree
rightMost.right = right;
// Modify the right subtree
rightMost = modifytree(right);
return rightMost;
}
function printpre(curr) {
while (curr != null) {
console.log(curr.data + " ");
curr = curr.right;
}
}
let root = new Node(10);
root.left = new Node(8);
root.right = new Node(2);
root.left.left = new Node(3);
root.left.right = new Node(5);
modifytree(root);
printpre(root);
[Expected Approach - 2] Using Iterative Preorder Traversal - O(n) Time and O(n) Space
This can be easily done using Iterative preorder traversal. The idea is to maintain a variable prev which maintains the previous node of the preorder traversal. Every-time a new node is encountered, the node set its right to previous one and prev is made equal to the current node. In the end we will have a sort of linked list whose first element is root then left child then right, so on and so forth.
Below is the implementation of the above approach:
C++
// C++ code to modify binary tree for
// traversal using only right pointer
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int data;
Node* left;
Node* right;
Node(int x){
data = x;
left = right = nullptr;
}
};
// An iterative process to set the right
// pointer of Binary tree
void modifytree(Node* root) {
if (root == nullptr)
return;
// Create an empty stack and
// push root to it
stack<Node*> nodeStack;
nodeStack.push(root);
Node* pre = nullptr;
while (nodeStack.empty() == false) {
// Pop the top item from stack
Node* node = nodeStack.top();
nodeStack.pop();
// Push right and left children of
// the popped node to stack
if (node->right)
nodeStack.push(node->right);
if (node->left)
nodeStack.push(node->left);
// check if some previous node
// exists
if (pre != nullptr) {
// set the right pointer of
// previous node to current
pre->right = node;
}
pre = node;
}
}
void printpre(Node* root) {
while (root != nullptr) {
cout << root->data << " ";
root = root->right;
}
}
int main() {
// Constructed binary tree is
// 10
// / \
// 8 2
// / \
// 3 5
Node* root = new Node(10);
root->left = new Node(8);
root->right = new Node(2);
root->left->left = new Node(3);
root->left->right = new Node(5);
modifytree(root);
printpre(root);
return 0;
}
// Java code to modify binary tree for
// traversal using only right pointer
import java.util.Stack;
class Node {
int data;
Node left, right;
public Node(int x) {
data = x;
left = right = null;
}
}
class GfG {
// An iterative process to set the right
// pointer of Binary tree
static void modifytree(Node root) {
if (root == null)
return;
// Create an empty stack and push
// root to it
Stack<Node> nodeStack = new Stack<>();
nodeStack.push(root);
Node pre = null;
while (!nodeStack.isEmpty()) {
// Pop the top item from stack
Node node = nodeStack.pop();
// Push right and left children of the
// popped node to stack
if (node.right != null)
nodeStack.push(node.right);
if (node.left != null)
nodeStack.push(node.left);
// Check if some previous node exists
if (pre != null) {
// Set the right pointer of
// previous node to current
pre.right = node;
}
pre = node;
}
}
static void printpre(Node root) {
while (root != null) {
System.out.print(root.data + " ");
root = root.right;
}
}
public static void main(String[] args) {
// Constructed binary tree is
// 10
// / \
// 8 2
// / \
// 3 5
Node root = new Node(10);
root.left = new Node(8);
root.right = new Node(2);
root.left.left = new Node(3);
root.left.right = new Node(5);
modifytree(root);
printpre(root);
}
}
# Python code to modify binary tree
# for traversal using only right pointer
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
# An iterative process to set the right
# pointer of Binary tree
def modifytree(root):
if root is None:
return
# Create an empty stack and push
# root to it
nodeStack = []
nodeStack.append(root)
pre = None
while nodeStack:
# Pop the top item from stack
node = nodeStack.pop()
# Push right and left children of
# the popped node to stack
if node.right:
nodeStack.append(node.right)
if node.left:
nodeStack.append(node.left)
# Check if some previous node exists
if pre is not None:
# Set the right pointer of
# previous node to current
pre.right = node
pre = node
def printpre(root):
while root is not None:
print(root.data, end=" ")
root = root.right
if __name__ == "__main__":
# Constructed binary tree is
# 10
# / \
# 8 2
# / \
# 3 5
root = Node(10)
root.left = Node(8)
root.right = Node(2)
root.left.left = Node(3)
root.left.right = Node(5)
modifytree(root)
printpre(root)
// C# code to modify binary tree for
// traversal using only right pointer
using System;
using System.Collections.Generic;
class Node {
public int data;
public Node left, right;
public Node(int x) {
data = x;
left = right = null;
}
}
class GfG {
// An iterative process to set the
// right pointer of Binary tree
static void modifytree(Node root) {
if (root == null)
return;
// Create an empty stack and push root to it
Stack<Node> nodeStack = new Stack<Node>();
nodeStack.Push(root);
Node pre = null;
while (nodeStack.Count > 0) {
// Pop the top item from stack
Node node = nodeStack.Pop();
// Push right and left children of
// the popped node to stack
if (node.right != null)
nodeStack.Push(node.right);
if (node.left != null)
nodeStack.Push(node.left);
// Check if some previous node exists
if (pre != null) {
pre.right = node;
}
pre = node;
}
}
static void printpre(Node root) {
while (root != null) {
Console.Write(root.data + " ");
root = root.right;
}
}
static void Main(string[] args) {
// Constructed binary tree is
// 10
// / \
// 8 2
// / \
// 3 5
Node root = new Node(10);
root.left = new Node(8);
root.right = new Node(2);
root.left.left = new Node(3);
root.left.right = new Node(5);
modifytree(root);
printpre(root);
}
}
// JavaScript code to modify binary tree
// for traversal using only right pointer
class Node {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
}
// An iterative process to set the right
// pointer of Binary tree
function modifytree(root) {
if (root === null) return;
// Create an empty stack and push
// root to it
const nodeStack = [];
nodeStack.push(root);
let pre = null;
while (nodeStack.length > 0) {
// Pop the top item from stack
const node = nodeStack.pop();
// Push right and left children of
// the popped node to stack
if (node.right !== null) nodeStack.push(node.right);
if (node.left !== null) nodeStack.push(node.left);
// Check if some previous node exists
if (pre !== null) {
pre.right = node;
}
pre = node;
}
}
function printpre(root) {
while (root !== null) {
console.log(root.data + " ");
root = root.right;
}
}
const root = new Node(10);
root.left = new Node(8);
root.right = new Node(2);
root.left.left = new Node(3);
root.left.right = new Node(5);
modifytree(root);
printpre(root);
Similar Reads
Binary Tree Data Structure A Binary Tree Data Structure is a hierarchical data structure in which each node has at most two children, referred to as the left child and the right child. It is commonly used in computer science for efficient storage and retrieval of data, with various operations such as insertion, deletion, and
3 min read
Introduction to Binary Tree Binary Tree is a non-linear and hierarchical data structure where each node has at most two children referred to as the left child and the right child. The topmost node in a binary tree is called the root, and the bottom-most nodes are called leaves. Introduction to Binary TreeRepresentation of Bina
15+ min read
Properties of Binary Tree This post explores the fundamental properties of a binary tree, covering its structure, characteristics, and key relationships between nodes, edges, height, and levelsBinary tree representationNote: Height of root node is considered as 0. Properties of Binary Trees1. Maximum Nodes at Level 'l'A bina
4 min read
Applications, Advantages and Disadvantages of Binary Tree A binary tree is a tree that has at most two children for any of its nodes. There are several types of binary trees. To learn more about them please refer to the article on "Types of binary tree" Applications:General ApplicationsDOM in HTML: Binary trees help manage the hierarchical structure of web
2 min read
Binary Tree (Array implementation) Given an array that represents a tree in such a way that array indexes are values in tree nodes and array values give the parent node of that particular index (or node). The value of the root node index would always be -1 as there is no parent for root. Construct the standard linked representation o
6 min read
Maximum Depth of Binary Tree Given a binary tree, the task is to find the maximum depth of the tree. The maximum depth or height of the tree is the number of edges in the tree from the root to the deepest node.Examples:Input: Output: 2Explanation: The longest path from the root (node 12) goes through node 8 to node 5, which has
11 min read
Insertion in a Binary Tree in level order Given a binary tree and a key, the task is to insert the key into the binary tree at the first position available in level order manner.Examples:Input: key = 12 Output: Explanation: Node with value 12 is inserted into the binary tree at the first position available in level order manner.Approach:The
8 min read
Deletion in a Binary Tree Given a binary tree, the task is to delete a given node from it by making sure that the tree shrinks from the bottom (i.e. the deleted node is replaced by the bottom-most and rightmost node). This is different from BST deletion. Here we do not have any order among elements, so we replace them with t
12 min read
Enumeration of Binary Trees A Binary Tree is labeled if every node is assigned a label and a Binary Tree is unlabelled if nodes are not assigned any label. Below two are considered same unlabelled trees o o / \ / \ o o o o Below two are considered different labelled trees A C / \ / \ B C A B How many different Unlabelled Binar
3 min read
Types of Binary Tree