Tree in LISP

Last Updated : 21 Jul, 2022

A tree is a non-linear hierarchical data structure that consists of nodes that are connected by edges. Tree stores data in a non-sequential manner so that operations like addition, deletion, updating, or searching could be performed in much less time than what it would take in linear data structures.

Tree traversal take logarithmic time for basic operations, while for linear data structures with the increase in size the time complexity increases linearly. Hence tree traversals are faster because log(n)<n.

In Lisp, to make a tree we use con cells, as lists of lists. We traverse through con cells for performing preorder, post-order, and in-order traversal.

Different Tree Functions in Lisp:

Lisp has some pre-defined functions which we could use on tree-data structures.

S.No.	Function	Description
1	copy-tree x & optional vecp	It returns a copy of the tree of cons cells x. It recursively copies both the car and the cdr directions. If x is not a cons cell, the function simply returns x unchanged. If the optional vecp argument is true, this function copies vectors (recursively) as well as cons cells.
2	tree-equal x y & key :test :test-not :key	It compares two trees of cons cells. If x and y are both cons cells, their cars and cdrs are compared recursively. If neither x nor y is a cons cell, they are compared by eql, or according to the specified test. The :key function, if specified, is applied to the elements of both trees.
3	subst new old tree & key :test :test-not :key	Old items are replaced (substituted) with a new item, in a tree, which is a tree of cons cells.
4	nsubst new old tree & key :test :test-not :key	It works the same as subst, the only difference is that it destroys the original tree.
5	sublis alist tree & key :test :test-not :key	It works like subst, except that it takes an association list alist of old-new pairs. Each element of the tree (after applying the :key function), is compared with the cars of alist; if it matches, it is replaced by the corresponding cdr.
6	nsublis alist tree & key :test :test-not :key	It works the same as sublis, but it is a destructive version.

In lisp, the car represents the first element of the list. cdr represents the rest of the list leaving the first element. car and cdr does not remove any elements from the list it just returns a report of what the elements are

Building Your Own Tree:

With the help of the tree and list functions, we can make a tree as follows:

Step 1: Function to create a node with data items in it.

Lisp

; the below function creates a node with items in it.

(defun make-tree (item)
   (cons (cons item nil) nil)
)

Step 2: Function to add child nodes.

Lisp

;  Function below will take two tree nodes and 
; add the second tree as the child of the first.

(defun add-child (tree child)
   (setf (car tree) (append (car tree) child))
   tree
)

Step 3: Function to define the first child.

Lisp

;  Function below will take a tree node and return
;  the first child of that node or nil, 
;  if this node does not have any child node.

(defun first-child (tree)
   (if (null tree)
      nil
      (cdr (car tree))
   )
)

Step 4: Function to return the next sibling of a given node.

Lisp

; it takes a tree node as argument, 
; and returns a reference to the next sibling node, 
; or nil, if the node does not have any

(defun next-sibling (tree)
   (cdr tree)
)

Step 5: Function to return the information in a node.

Lisp

;a function to return the information in a node

(defun data (tree)
   (car (car tree))
)

Now let us build a whole tree by combining the codes written above in a single file.

Example:

Lisp

; Code for aLisp tree
; the below function creates a node with items in it.
(defun make-tree (item)
   (cons (cons item nil) nil)
)

;  Function below will take two tree 
;  nodes and add the second tree as the child of the 
;  first.
(defun add-child (tree child)
   (setf (car tree) (append (car tree) child))
   tree
)

;  Function below will take a tree node and return
; the first child of that node or nil, 
;  if this node does not have any child node.
(defun first-child (tree)
   (if (null tree)
      nil
      (cdr (car tree))
   )
)
;  it takes a tree node as argument, and returns 
; a reference to the next sibling node,
;  or nil, if the node does not have any

(defun next-sibling (tree)
   (cdr tree)
)

;a function to return the information in a node
(defun data (tree)
   (car (car tree))
)


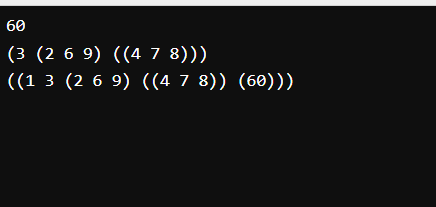
(setq tree '((1 3 (2 6 9) ( (4 7 8)))))
(setq mytree (make-tree 60))

(write (data mytree))
(terpri)
(write (first-child tree))
(terpri)
(setq newtree (add-child tree mytree))
(terpri)
(write newtree)