As noted in the previous chapters, Python's for loop works with collections. When working with materialized collections such as tuples, lists, maps, and sets, the for loop involves the explicit management of states. While this strays from purely functional programming, it reflects a necessary optimization for Python. If we assume that state management is localized to an iterator object that's created as a part of the for statement evaluation, we can leverage this feature without straying too far from pure, functional programming. If, for example, we use the for loop variable outside the indented body of the loop, we've strayed from purely functional programming by leveraging this state control variable.

We'll return to this in Chapter 6, Recursions and Reductions. It's an important topic, and we'll just scratch the surface here with a quick example of working with generators.

One common application of for loop iterable processing is the unwrap(process(wrap(iterable))) design pattern. A wrap() function will first transform each item of an iterable into a two-tuple with a derived sort key and the original item. We can then process these two-tuple items as a single, wrapped value. Finally, we'll use an unwrap() function to discard the value used to wrap, which recovers the original item.

This happens so often in a functional context that two functions are used heavily for this; they are the following:

fst = lambda x: x[0] 
snd = lambda x: x[1] 

These two functions pick the first and second values from a two-tuple, and both are handy for the process() and unwrap() functions.

Another common pattern is wrap3(wrap2(wrap1())). In this case, we're starting with simple tuples and then wrapping them with additional results to build up larger and more complex tuples. A common variation on this theme builds new, more complex namedtuple instances from source objects. We can summarize both of these as the Accretion design pattern—an item that accretes derived values.

As an example, consider using the accretion pattern to work with a simple sequence of latitude and longitude values. The first step will convert the simple point represented as a (lat, lon) pair on a path into pairs of legs (begin, end). Each pair in the result will be represented as ((lat, lon), (lat, lon)). The value of fst(item) is the starting position; the value of snd(item) is the ending position for each value of each item in the collection.

In the next sections, we'll show you how to create a generator function that will iterate over the content of a file. This iterable will contain the raw input data that we will process. 

Once we have the raw data, later sections will show how to decorate each leg with the haversine distance along the leg. The final result of a wrap(wrap(iterable())) design will be a sequence of three tuples—((lat, lon), (lat, lon), distance). We can then analyze the results for the longest and shortest distance, bounding rectangle, and other summaries.

We'll start by parsing an Extensible Markup Language (XML) file to get the raw latitude and longitude pairs. This will show you how we can encapsulate some not-quite-functional features of Python to create an iterable sequence of values.

We'll make use of the xml.etree module. After parsing, the resulting ElementTree object has a findall() method that will iterate through the available values.

We'll be looking for constructs, such as the following XML example:

<Placemark><Point> 
<coordinates>-76.33029518659048,
    37.54901619777347,0</coordinates> 
</Point></Placemark> 

The file will have a number of <Placemark> tags, each of which has a point and coordinate structure within it. This is typical of Keyhole Markup Language (KML) files that contain geographic information.

Parsing an XML file can be approached at two levels of abstraction. At the lower level, we need to locate the various tags, attribute values, and content within the XML file. At a higher level, we want to make useful objects out of the text and attribute values.

The lower-level processing can be approached in the following way:

import xml.etree.ElementTree as XML
from typing import Text, List, TextIO, Iterable
def row_iter_kml(file_obj: TextIO) -> Iterable[List[Text]]:
    ns_map= {
        "ns0": "http://www.opengis.net/kml/2.2",
        "ns1": "http://www.google.com/kml/ext/2.2"}
    path_to_points= ("./ns0:Document/ns0:Folder/ns0:Placemark/"
             "ns0:Point/ns0:coordinates")
    doc= XML.parse(file_obj)
    return (comma_split(Text(coordinates.text))
            for coordinates in 
            doc.findall(path_to_points, ns_map))

This function requires text from a file opened via a with statement. The result is a generator that creates list objects from the latitude/longitude pairs. As a part of the XML processing, this function includes a simple static dict object, ns_map, that provides the namespace mapping information for the XML tags we'll be searching. This dictionary will be used by the ElementTree.findall() method.

The essence of the parsing is a generator function that uses the sequence of tags located by doc.findall(). This sequence of tags is then processed by a comma_split() function to tease the text value into its comma-separated components.

The comma_split() function is the functional version of the split() method of a string, which is as follows:

def comma_split(text: Text) -> List[Text]:
    return text.split(",")

We've used the functional wrapper to emphasize a slightly more uniform syntax. We've also added explicit type hints to make it clear that text is converted to a list of text values. Without the type hint, there are two potential definitions of split() that could be meant. The method applies to bytes as well as str. We've used the Text type name, which is an alias for str in Python 3.

The result of the row_iter_kml() function is an iterable sequence of rows of data. Each row will be a list composed of three strings—latitude, longitude, and altitude of a way point along this path. This isn't directly useful yet. We'll need to do some more processing to get latitude and longitude as well as converting these two numbers into useful floating-point values.

This idea of an iterable sequence of tuples (or lists) allows us to process some kinds of data files in a simple and uniform way. In Chapter 3, Functions, Iterators, and Generators, we looked at how Comma Separated Values (CSV) files are easily handled as rows of tuples. In Chapter 6, Recursions and Reductions, we'll revisit the parsing idea to compare these various examples.

The output from the preceding function looks like the following example:

[['-76.33029518659048', '37.54901619777347', '0'], 
 ['-76.27383399999999', '37.840832', '0'], 
 ['-76.459503', '38.331501', '0'], 
 etc. 
 ['-76.47350299999999', '38.976334', '0']]

Each row is the source text of the <ns0:coordinates> tag split using the (,) that's part of the text content. The values are the east-west longitude, north-south latitude, and altitude. We'll apply some additional functions to the output of this function to create a usable subset of this data.

Once we've parsed the low-level syntax to transform XML to Python, we can restructure the raw data into something usable in our Python program. This kind of structuring applies to XML, JavaScript Object Notation (JSON), CSV, and any of the wide variety of physical formats in which data is serialized.

We'll aim to write a small suite of generator functions that transforms the parsed data into a form our application can use. The generator functions include some simple transformations on the text that are found by the row_iter_kml() function, which are as follows:

• Discarding altitude can also be stated as keeping only latitude and longitude
• Changing the order from (longitude, latitude) to (latitude, longitude)

We can make these two transformations have more syntactic uniformity by defining a utility function, as follows:

def pick_lat_lon(
  lon: Text, lat: Text, alt: Text) -> Tuple[Text, Text]:
    return lat, lon

We've created a function to take three argument values and created a tuple from two of them. The type hints are more complex than the function itself.

We can use this function as follows:

from typing import Text, List, Iterable

Rows = Iterable[List[Text]]
LL_Text = Tuple[Text, Text]
def lat_lon_kml(row_iter: Rows) -> Iterable[LL_Text]:
    return (pick_lat_lon(*row) for row in row_iter)

This function will apply the pick_lat_lon() function to each row from a source iterator. We've used *row to assign each element of the row-three tuple to separate parameters of the pick_lat_lon() function. The function can then extract and reorder the two relevant values from each three-tuple.

To simplify the function definition, we've defined two type aliases: Rows and LL_Text. These type aliases can simplify a function definition. They can also be reused to ensure that several related functions are all working with the same types of objects.

This kind of functional design allows us to freely replace any function with its equivalent, which makes refactoring quite simple. We tried to achieve this goal when we provided alternative implementations of the various functions. In principle, a clever functional language compiler may do some replacements as a part of an optimization pass.

These functions can be combined to parse the file and build a structure we can use. Here's an example of some code that could be used for this purpose:

url = "file:./Winter%202012-2013.kml"
with urllib.request.urlopen(url) as source:
    v1= tuple(lat_lon_kml(row_iter_kml(source)))
print(v1)

This script uses the urllib command to open a source. In this case, it's a local file. However, we can also open a KML file on a remote server. Our objective in using this kind of file opening is to ensure that our processing is uniform no matter what the source of the data is.

The script is built around the two functions that do low-level parsing of the KML source. The row_iter_kml(source) expression produces a sequence of text columns. The lat_lon_kml() function will extract and reorder the latitude and longitude values. This creates an intermediate result that sets the stage for further processing. The subsequent processing is independent of the original format.

When we run this, we see results such as the following:

(('37.54901619777347', '-76.33029518659048'), 
 ('37.840832', '-76.27383399999999'), 
 ('38.331501', '-76.459503'), 
 ('38.330166', '-76.458504'), 
 ('38.976334', '-76.47350299999999'))

We've extracted just the latitude and longitude values from a complex XML file using an almost purely functional approach. As the result is iterable, we can continue to use functional programming techniques to process each point that we retrieve from the file.

We've explicitly separated low-level XML parsing from higher-level reorganization of the data. The XML parsing produced a generic tuple of string structure. This is compatible with the output from the CSV parser. When working with SQL databases, we'll have a similar iterable of tuple structures. This allows us to write code for higher-level processing that can work with data from a variety of sources.

We'll show you a series of transformations to re-arrange this data from a collection of strings to a collection of waypoints along a route. This will involve a number of transformations. We'll need to restructure the data as well as convert from strings to floating-point values. We'll also look at a few ways to simplify and clarify the subsequent processing steps. We'll use this dataset in later chapters because it's quite complex.

A common restructuring requirement is to make start-stop pairs out of points in a sequence. Given a sequence, , we would also want to create a paired sequence, . The first and second items form a pair. The second and third items form the next pair. When doing time-series analysis, we may be combining more widely separated values. In this example, the pairs are immediately adjacent values.

A paired sequence will allow us to use each pair to compute distances from point to point using a trivial application of a haversine function. This technique is also used to convert a path of points into a series of line segments in a graphics, application.

Why pair up items? Why not do something such as this:

begin= next(iterable)
for end in iterable:
    compute_something(begin, end)
    begin = end  

This, clearly, will process each leg of the data as a begin-end pair. However, the processing function and the loop that restructures the data are tightly bound, making reuse more complex than necessary. The algorithm for pairing is hard to test in isolation because it's bound to the compute_something() function.

This combined function also limits our ability to reconfigure the application. There's no easy way to inject an alternative implementation of the compute_something() function. Additionally, we've got a piece of an explicit state, the begin variable, which makes life potentially complex. If we try to add features to the body of loop, we can easily fail to set the begin variable correctly if a point is dropped from consideration. A filter() function introduces an if statement that can lead to an error in updating the begin variable.

We achieve better reuse by separating this simple pairing function. This, in the long run, is one of our goals. If we build up a library of helpful primitives such as this pairing function, we can tackle problems more quickly and confidently.

There are many ways to pair up the points along the route to create start and stop information for each leg. We'll look at a few here and then revisit this in Chapter 5, Higher-Order Functions, and again in Chapter 7, The Itertools Module. Creating pairs can be done in a purely functional way using a recursion.

The following code is one version of a function to pair up the points along a route:

from typing import Iterator, Any
Item_Iter = Iterator[Any]
Pairs_Iter = Iterator[Tuple[float, float]]
def pairs(iterator: Item_Iter) -> Pairs_Iter:
    def pair_from(
            head: Any, 
            iterable_tail: Item_Iter) -> Pairs_Iter:
        nxt= next(iterable_tail)
        yield head, nxt
        yield from pair_from(nxt, iterable_tail)

    try:
        return pair_from(next(iterator), iterator)
    except StopIteration:
         return iter([])

The essential work is done by the internal pair_from() function. This works with the item at the head of an iterator plus the iterator object itself. It yields the first pair, pops the next item from the iterable, and then invokes itself recursively to yield any additional pairs.

The type hints state the parameter, iterator, must be of type Item_Iter. The result is of the Pairs_Iter type, an iterator over two-tuples, where each item is a float type. These are hints used by the mypy program to check that our code is likely to work. The type hint declarations are contained in the typing module.

The input must be an iterator that responds to the next() function. To work with a collection object, the iter() function must be used explicitly to create an iterator from the collection.

We've invoked the pair_from() function from the pairs() function. The pairs() function ensures that the initialization is handled properly by getting the initial item from the iterator argument. In the rare case of an empty iterator, the initial call to next() will raise a StopIteration exception; this situation will create an empty iterable.

Our strategy for performing tail-call optimization is to replace the recursion with a generator expression. We can clearly optimize this recursion into a simple for loop. The following code is another version of a function to pair up the points along a route:

from typing import Iterator, Any, Iterable, TypeVar
T_ = TypeVar('T_')
Pairs_Iter = Iterator[Tuple[T_, T_]]
def legs(lat_lon_iter: Iterator[T_]) -> Pairs_Iter:
    begin = next(lat_lon_iter)
    for end in lat_lon_iter:
        yield begin, end
        begin = end  

The version is quite fast and free from stack limits. It's independent of any particular type of sequence, as it will pair up anything emitted by a sequence generator. As there's no processing function inside the loop, we can reuse the legs() function as needed.

The type variable, T_, created with the TypeVar function, is used to clarify precisely how the legs() function restructures the data. The hint says that the input type is preserved on output. The input type is an Iterator of some arbitrary type, T_; the output will include tuples of the same type, T_. No other conversion is implied by the function.

The begin and end variables maintain the state of the computation. The use of stateful variables doesn't fit the ideal of using immutable objects for functional programming. The optimization is important. It's also invisible to users of the function, making it a Pythonic functional hybrid.

We can think of this function as one that yields the following kind of sequence of pairs:

list[0:1], list[1:2], list[2:3], ..., list[-2:]

Another view of this function is as follows:

zip(list, list[1:])

While informative, this zip-based version only work for sequence objects. The legs() and pairs() functions work for any iterable, including sequence objects.

The purely functional viewpoint is that all of our iterables can be processed with recursive functions, where the state is merely the recursive call stack. Pragmatically, Python iterables will often involve evaluation of other for loops. There are two common situations: collection objects and iterables. When working with a collection object, an iterator object is created by the for statement. When working with a generator function, the generator function is an iterator and maintains its own internal state. Often, these are equivalent, from a Python programming perspective. In rare cases—generally those situations where we have to use an explicit next() function—two won't be precisely equivalent.

The legs() function shown previously has an explicit next() evaluation to get the first value from the iterable. This works wonderfully well with generator functions, expressions, and other iterables. It doesn't work with sequence objects such as tuples or lists.

The following code contains three examples to clarify the use of the next() and iter() functions:

>>> list(legs(x for x in range(3)))
[(0, 1), (1, 2)]
>>> list(legs([0,1,2]))
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "<stdin>", line 2, in legs
TypeError: 'list' object is not an iterator
>>> list(legs(iter([0,1,2])))
[(0, 1), (1, 2)]  

In the first case, we applied the legs() function to an iterable. In this case, the iterable was a generator expression. This is the expected behavior based on our previous examples in this chapter. The items are properly paired up to create two legs from three waypoints.

In the second case, we tried to apply the legs() function to a sequence. This resulted in an error. While a list object and an iterable are equivalent when used in a for statement, they aren't equivalent everywhere. A sequence isn't an iterator; it doesn't implement the next() function. The for statement handles this gracefully, however, by creating an iterator from a sequence automatically.

To make the second case work, we need to explicitly create an iterator from a list object. This permits the legs() function to get the first item from the iterator over the list items. The iter() function will create an iterator from a list.

We have two kinds of extensions we could factor into a simple loop. We'll look first at a filter extension. In this case, we may be rejecting values from further consideration. They may be data outliers, or perhaps source data that's improperly formatted. Then, we'll look at mapping source data by performing a simple transformation to create new objects from the original objects. In our case, we'll be transforming strings to floating-point numbers. The idea of extending a simple for statement with a mapping, however, applies to many situations. We'll look at refactoring the above pairs() function. What if we need to adjust the sequence of points to discard a value? This will introduce a filter extension that rejects some data values.

The loop we're designing simply returns pairs without performing any additional application-related processing—the complexity is minimal. Simplicity means we're somewhat less likely to confuse the processing state.

Adding a filter extension to this design could look something like the following code snippet:

from typing import Iterator, Any, Iterable
Pairs_Iter = Iterator[Tuple[float, float]]
LL_Iter = Iterable[
    Tuple[Tuple[float, float], Tuple[float, float]]]
def legs_filter(lat_lon_iter: Pairs_Iter) -> LL_Iter:
    begin = next(lat_lon_iter)
    for end in lat_lon_iter:
        if #some rule for rejecting:
            continue
        yield begin, end
        begin = end  

We have plugged in a processing rule to reject certain values. As the loop remains succinct and expressive, we are confident that the processing will be done properly. Also, we can easily write a test for this function, as the results work for any iterable, irrespective of the long-term destination of the pairs.

We haven't really provided much information about the #some rule for rejecting code. This is a kind of condition that uses begin, end, or both variables to reject the point from further consideration. For example, it may reject begin == end to avoid zero-length legs.

The next refactoring will introduce additional mapping to a loop. Adding mappings is common when a design is evolving. In our case, we have a sequence of string values. We need to convert these to float values for later use. This is a relatively simple mapping that shows the design pattern.

The following is one way to handle this data mapping, through a generator expression that wraps a generator function:

trip = list(
    legs(
        (float(lat), float(lon)) 
        for lat,lon in lat_lon_kml(row_iter_kml(source))
    )
)

We've applied the legs() function to a generator expression that creates float values from the output of the lat_lon_kml() function. We can read this in the opposite order as well. The lat_lon_kml() function's output is transformed into a pair of float values, which is then transformed into a sequence of legs.

This is starting to get complex. We've got a large number of nested functions here. We're applying float(), legs(), and list() to a data generator. One common way of refactoring complex expressions is to separate the generator expression from any materialized collection. We can do the following to simplify the expression:

ll_iter = (
    (float(lat), float(lon)) 
    for lat,lon in lat_lon_kml(row_iter_kml(source))
)
print(tuple(legs(ll_iter)))

We've assigned the generator function to a variable named ll_iter. This variable isn't a collection object; it's a generator of item. We're not using a list comprehension to create an object. We've merely assigned the generator expression to a variable name. We've then used the flt variable in another expression.

The evaluation of the tuple() method actually leads to a proper object being built so that we can print the output. The flt variable's objects are created only as needed.

There is other refactoring we might like to do. In general, the source of the data is something we often want to change. In our example, the lat_lon_kml() function is tightly bound in the rest of the expression. This makes reuse difficult when we have a different data source.

In the case where the float() operation is something we'd like to parameterize so that we can reuse it, we can define a function around the generator expression. We'll extract some of the processing into a separate function merely to group the operations. In our case, the string-pair to float-pair is unique to particular source data. We can rewrite a complex float-from-string expression into a simpler function, such as:

from typing import Iterator, Tuple, Text, Iterable
Text_Iter = Iterable[Tuple[Text, Text]]
LL_Iter = Iterable[Tuple[float, float]]
def float_from_pair(lat_lon_iter: Text_Iter) -> LL_Iter:
    return (
        (float(lat), float(lon)) 
        for lat,lon in lat_lon_iter
    )

The float_from_pair() function applies the float() function to the first and second values of each item in the iterable, yielding a two-tuple of floats created from an input value. We've relied on Python's for statement to decompose the two-tuple.

The type hints insist that the input matches the Text_Iter type alias—it must be an iterable source of pairs of Text values. The result uses the LL_Iter type alias—this must be an iterable of pairs of float values. The LL_Iter type alias may be used elsewhere in a complex set of function definitions.

We can use this function in the following context:

legs(
    float_from_pair(
        lat_lon_kml(
            row_iter_kml(source))))  

We're going to create legs that are built from float values that come from a KML file. It's fairly easy to visualize the processing, as each stage in the process is a simple prefix function. Each function's input is the output from the next function in the nested processing steps.

When parsing, we often have sequences of string values. For numeric applications, we'll need to convert strings to float, int, or Decimal values. This often involves inserting a function such as the float_from_pair() function into a sequence of expressions that clean up the source data.

Our previous output was all strings; it looked like the following code snippet:

(('37.54901619777347', '-76.33029518659048'), 
 ('37.840832', '-76.27383399999999'), 
 ... 
 ('38.976334', '-76.47350299999999'))  

We'll want data like the following code snippet, where we have floats:

(((37.54901619777347, -76.33029518659048), 
 (37.840832, -76.273834)), ((37.840832, -76.273834), 
 ... 
 ((38.330166, -76.458504), (38.976334, -76.473503)))
  

We'll need to create a pipeline of simpler transformation functions. Here, we arrived at flt= ((float(lat), float(lon)) for lat,lon in lat_lon_kml(...)). We can exploit the substitution rule for functions and replace a complex expression such as (float(lat), float(lon)) for lat,lon in lat_lon_kml(...)) with a function that has the same value, in this case float_from_pair(lat_lon_kml(...)). This kind of refactoring allows us to be sure that the simplification has the same effect as a more complex expression.

There are some simplifications that we'll look at in Chapter 5, Higher-Order Functions. We will revisit this in Chapter 6, Recursions and Reductions, to see how to apply these simplifications to the file-parsing problem.

We'll look at a more complex kind of generator expression to map data values from one kind of data to another. In this case, we'll apply a fairly complex function to individual data values created by a generator.

We'll call these non-generator functions scalar, as they work with simple atomic values. To work with collections of data, a scalar function will be embedded in a generator expression.

To continue the example started earlier, we'll provide a haversine function and then use a generator expression to apply a scalar haversine() function to a sequence of pairs from our KML file.

The haversine() function looks like the following code:

from math import radians, sin, cos, sqrt, asin
from typing import Tuple
    
MI= 3959
NM= 3440
KM= 6371
    
Point = Tuple[float, float]
def haversine(p1: Point, p2: Point, R: float=NM) -> float:
    lat_1, lon_1= p1
    lat_2, lon_2= p2
    Δ_lat = radians(lat_2 - lat_1)
    Δ_lon = radians(lon_2 - lon_1)
    lat_1 = radians(lat_1)
    lat_2 = radians(lat_2)
    a = sqrt(
        sin(Δ_lat/2)**2 +
        cos(lat_1)*cos(lat_2)*sin(Δ_lon/2)**2
    )
    c = 2*asin(a)
    return R * c  

This is a relatively simple implementation copied from the World Wide Web. The start and end points have type hints. The return value is also provided with a hint. The explicit use of Point = Tuple[float, float] makes it possible for the mypy tool to confirm that this function is used properly.

The following code is how we could use our collection of functions to examine some KML data and produce a sequence of distances:

trip= (
    (start, end, round(haversine(start, end),4))
    for start,end in
        legs(float_from_pair(lat_lon_kml()))
)

for start, end, dist in trip:
    print(start, end, dist)

The essence of the processing is the generator expression assigned to the trip variable. We've assembled three tuples with a start, end, and the distance from start to end. The start and end pairs come from the legs() function. The legs() function works with floating-point data built from the latitude-longitude pairs extracted from a KML file.

The output looks like the following command snippet:

(37.54901619777347, -76.33029518659048) (37.840832, -76.273834) 17.7246
(37.840832, -76.273834) (38.331501, -76.459503) 30.7382
(38.331501, -76.459503) (38.845501, -76.537331) 31.0756
(36.843334, -76.298668) (37.549, -76.331169) 42.3962
(37.549, -76.331169) (38.330166, -76.458504) 47.2866
(38.330166, -76.458504) (38.976334, -76.473503) 38.8019
  

Each individual processing step has been defined succinctly. The overview, similarly, can be expressed succinctly as a composition of functions and generator expressions.

Clearly, there are several further processing steps we may like to apply to this data. The first, of course, is to use the format() method of a string to produce better-looking output.

More importantly, there are a number of aggregate values we'd like to extract from this data. We'll call these values reductions of the available data. We'd like to reduce the data to get the maximum and minimum latitude, for example, to show the extreme north and south ends of this route. We'd like to reduce the data to get the maximum distance in one leg as well as the total distance for all legs.

The problem we'll have using Python is that the output generator in the trip variable can be used only once. We can't easily perform several reductions of this detailed data. We can use itertools.tee() to work with the iterable several times. It seems wasteful, however, to read and parse the KML file for each reduction.

We can make our processing more efficient by materializing intermediate results. We'll look at this in the next section. Then we will see how to compute multiple reductions of the available data.

The any() and all() functions provide boolean reduction capabilities. Both functions reduce a collection of values to a single True or False. The all() function ensures that all values are True. The any() function ensures that at least one value is True.

These functions are closely related to a universal quantifier and an existential quantifier used to express mathematical logic. We may, for example, want to assert that all elements in a given collection have a property. One formalism for this could look like the following:

We read this as for all x in S, the function, Prime(x), is true. We've put a quantifier, for all, in front of the logical expression.

In Python we switch the order of the items slightly to transcribe the logic expression as follows:

all(isprime(x) for x in someset)  

This will evaluate the isprime(x) function for each distinct value of x and reduce the collection of values to a single True or False.

The any() function is related to the existential quantifier. If we want to assert that no value in a collection is prime, we could use one of these two equivalent expressions:

The first states that it is not the case that all elements in S are prime. The second version asserts that there exists one element in S that is not prime. These two are equivalent, that is if not all elements are prime, then one element must be non-prime.

In Python, we can switch the order of the terms and transcribe these to working code as follows:

not all(isprime(x) for x in someset)
any(not isprime(x) for x in someset)  

As they're equivalent, there are two reasons for preferring one over the other: performance and clarity. The performance is nearly identical, so it boils down to clarity. Which of these states the condition the most clearly?

The all() function can be described as an and reduction of a set of values. The result is similar to folding the and operator between the given sequence of values. The any() function, similarly, can be described as an or reduction. We'll return to this kind of general purpose reducing when we look at the reduce() function in Chapter 10, The Functools Module. There's no best answer here; it's a question of what seems most readable to the intended audience.

We also need to look at the degenerate case of these functions. What if the sequence has no elements? What are the values of all(()) or all([])?

If we ask, "Are all the elements in an empty set prime? Then what's the answer? For guidance on this, we'll expand the question slightly, and look at the idea of an identity element.

If we ask, "Are all the elements in an empty set prime, and are all the elements in SomeSet prime?" we have a hint as to how we have to proceed. We're performing an and reduction of an empty set and an and reduction of SomeSet:

It turns out that the and operator can be distributed freely. We can rewrite this to, as a union of the two sets, which is then evaluated for being prime:

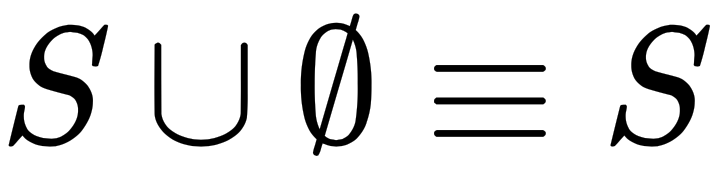Clearly, . If we union a set, S, with an empty set, we get the original set, S. The empty set can be called the union identify element. This is parallel to the way zero is the additive identity element:

Similarly, any(()) must be the or identity element, which is False. If we think of the multiplicative identify element, 1, where , then all(()) must be True.

The following code demonstrates that Python follows these rules:

>>> all(())
True
>>> any(())
False  

Python gives us some very nice tools to perform processing that involves logic. We have the built-in and, or, and not operators. However, we also have these collection-oriented any() and all() functions.

The len() and sum() functions provide two simple reductions—a count of the elements and the sum of the elements in a sequence. These two functions are mathematically similar, but their Python implementation is quite different.

Mathematically, we can observe this cool parallelism. The len() function returns the sum of ones for each value in a collection, .

The sum() function returns the sum of x for each value in a collection, .

The sum() function works for any iterable. The len() function doesn't apply to iterables; it only applies to sequences. This little asymmetry in the implementation of these functions is a little awkward around the edges of statistical algorithms.

For empty sequences, both of these functions return a proper additive identity element of zero:

>>> sum(())
0

Of course, sum(()) returns an integer zero. When other numeric types are used, the integer zero will be coerced to the proper type for the available data.

The definitions of the arithmetic mean have an appealingly trivial definition based on sum() and len(), which is as follows:

def mean(items):
    return sum(items)/len(items)

While elegant, this doesn't actually work for iterables. This definition only works for collections that support the len() function. This is easy to discover when trying to write proper type annotations. The definition of mean(items: Iterable)->float won't work because Iterable types don't support len().

Indeed, we have a hard time performing a simple computation of mean or standard deviation based on iterables. In Python, we must either materialize a sequence object or resort to somewhat more complex operations.

The definition needs to look like this:

from collections import Sequence
def mean(items: Sequence) -> float:
    return sum(items)/len(items)

This includes the appropriate type hints to assure that sum() and len() will both work.

We have some alternative and elegant expressions for mean and standard deviation in the following definitions:

import math
s0 = len(data)  # sum(x**0 for x in data)
s1 = sum(data)  # sum(x**1 for x in data)
s2 = sum(x**2 for x in data)
    
mean = s1/s0
stdev = math.sqrt(s2/s0 - (s1/s0)**2)  

These three sums, s0, s1, and s2, have a tidy, parallel structure. We can easily compute the mean from two of the sums. The standard deviation is a bit more complex, but it's based on the three available sums.

This kind of pleasant symmetry also works for more complex statistical functions, such as correlation and even least-squares linear regression.

The moment of correlation between two sets of samples can be computed from their standardized value. The following is a function to compute the standardized value:

def z(x: float, m_x: float, s_x: float) -> float:
    return (x-m_x)/s_x

The calculation is simply to subtract the mean, μ_x, from each sample, x, and divide by the standard deviation, σ_x. This gives us a value measured in units of sigma, σ. A value ±1 σ is expected about two-thirds of the time. Larger values should be less common. A value outside ±3 σ should happen less than one percent of the time.

We can use this scalar function as follows:

>>> d = [2, 4, 4, 4, 5, 5, 7, 9]
>>> list(z(x, mean(d), stdev(d)) for x in d)
[-1.5, -0.5, -0.5, -0.5, 0.0, 0.0, 1.0, 2.0]

We've materialized a list that consists of normalized scores based on some raw data in the variable, d. We used a generator expression to apply the scalar function, z(), to the sequence object.

The mean() and stdev() functions are simply based on the examples shown previously:

def mean(samples: Sequence) -> float:
    return s1(samples)/s0(samples)
def stdev(samples: Sequence) -> float:
    N= s0(samples) 
    return sqrt((s2(samples)/N)-(s1(samples)/N)**2)

The three sum functions, similarly, can be defined, instead of the lambda forms, as shown in the following code:

def s0(samples: Sequence) -> float:
    return sum(1 for x in samples) # or len(data)
def s1(samples: Sequence) -> float:
    return sum(x for x in samples) # or sum(data)
def s2(samples: Sequence) -> float:
    return sum(x*x for x in samples)  

While this is very expressive and succinct, it's a little frustrating because we can't simply use an iterable here. When computing a mean, both a sum of the iterable and a count of the iterable are required. For the standard deviation, two sums and a count of the iterable are all required. For this kind of statistical processing, we must materialize a sequence object so that we can examine the data multiple times.

The following code shows how we can compute the correlation between two sets of samples:

def corr(samples1: Sequence, samples2: Sequence) -> float:
    m_1, s_1 = mean(samples1), stdev(samples1)
    m_2, s_2 = mean(samples2), stdev(samples2)
    z_1 = (z( x, m_1, s_1 ) for x in samples1)
    z_2 = (z( x, m_2, s_2 ) for x in samples2)
    r = (sum(zx1*zx2 for zx1, zx2 in zip(z_1, z_2)) 
        / len(samples1))
    return r
  

This correlation function gathers basic statistical summaries of the two sets of samples: the mean and standard deviation. Given these summaries, we define two generator functions that will create normalized values for each set of samples. We can then use the zip() function (see the next example) to pair up items from the two sequences of normalized values and compute the product of those two normalized values. The average of the product of the normalized scores is the correlation.

The following code is an example of gathering the correlation between two sets of samples:

>>> # Height (m)
>>> xi= [1.47, 1.50, 1.52, 1.55, 1.57, 1.60, 1.63, 1.65,
...    1.68, 1.70, 1.73, 1.75, 1.78, 1.80, 1.83,]
>>> # Mass (kg)
>>> yi= [52.21,53.12,54.48,55.84,57.20,58.57,59.93,61.29,
...    63.11, 64.47, 66.28, 68.10, 69.92, 72.19, 74.46,] 
>>> round(corr( xi, yi ), 5)
0.99458  

We've shown you two sequences of data points, xi and yi. The correlation is over .99, which shows a very strong relationship between the two sequences.

This shows us one of the strengths of functional programming. We've created a handy statistical module using a half-dozen functions with definitions that are single expressions. The counterexample is the corr() function that can be reduced to a single very long expression. Each internal variable in this function is used just once; a local variable can be replaced with a copy and paste of the expression that created it. This shows us that the corr() function has a functional design, even though it's written out in six separate lines of Python.