Sparse Random Network Coding for Reliable Multicast Services
1 like642 views
The document discusses Sparse Random Network Coding (RNCC) for reliable multicast services in communication systems, emphasizing the computational complexity of RNCC decoders and proposing methods to optimize transmission parameters and sparsity. It presents a Markov chain performance analysis to model the process of coding matrix formation and provides numerical results for various implementations. The findings suggest that controlling sparsity improves decoding efficiency while maintaining battery life in mobile devices.
![6
๏ Encoding performed over each service layer independently
from the others.
๏ The source node will linearly combine the data packets
composing the l-th layer and will generate a
stream of coded packets, where
๏ is a layered source message of K source
packets, classified into L service layers
x = {x1, . . . , xK}
RNC in a Nutshell
kl
Coef:icients of the
linear combination
are selected over a
:inite :ield of size q
{xi}K`
i=K` 1+1
yj =
K`X
i=K` 1+1
cj,i · xi
k1 k2 k3
K3 = K
K2
K1
x1 x2 . . .. . . xK
Fig. 1. Layered source message, in the case of L = 3.
the scope of the paper to provide analytical and optimization
frameworks dealing with the compression strategy used to
generate a scalable service. For these reasons, the proposed
analysis has been made independent of the way service layers
are generated and the nature of the adopted service scalability.
As suggested in [12], [18], we model the transmitted service
use
rec
tha
SR
an
ide
pa
of
sys
is
to
sys](https://image.slidesharecdn.com/uobsparse-151012141945-lva1-app6892/85/Sparse-Random-Network-Coding-for-Reliable-Multicast-Services-6-320.jpg)
![RNC in a Nutshell
๏ When has rank equal to , the user can keep only the
linearly independent rows and invert the matrix.
8
Cu n` k`
Encoding Decoding
Cu · xT
` = yT
() C 1
u · yT
` = xT
`
๏ Given [1, 0] and [0, 1], is [2, 2] linearly independent?
✴ No, because 2[1, 0] + 2[0, 1] - [2, 2] = [0, 0]
๏ Given two lin. indep. vectors (a and b) in GF(q), how many
vectors form span({a,b})?
✴ q2. For a = [1, 0], b = [0, 1] and q = 2, span({a,b}) = {[0, 0],
[0, 1], [1, 0], [1, 1]]}
๏ Let us encode over a set of 5 inf. elements, if I collected 3 lin.
indep. coding vectors, what is the prob. of collecting a new lin.
dep. coding vec.?
✴ q3 / q5](https://image.slidesharecdn.com/uobsparse-151012141945-lva1-app6892/85/Sparse-Random-Network-Coding-for-Reliable-Multicast-Services-8-320.jpg)
![The Coding Matrix
๏ Matrix is a random matrix over GF(q), where elements are
independently and uniformly selected by the following prob. law
10
Cu
๏ If , all the GF(q) elements are equiprobable and things
are nice and easy… otherwise, things get tricky!
๏ Since 1997, only 2 conference papers and 2 (+1 on Arxiv) journal
papers deal with sparse random matrices.
cupied
vide an
mission
ice.
of K
essage.
ber kℓ
e MCS
service
e block
(mℓ)⌉.
source
nd are
cement
ize the
ill also
parsity
mized.
the transmission of each layer shall meet a temporal constraint.
The sparse versions of both the classic (S-RLNC) and
systematic implementation of RLNC (S-SRLNC) are obtained
as follows. Each component cj,i of a non-degenerate coding
vector associated with source message layer ℓ is independently
and identically distributed as follows [25]:
Pr (cj,i = v) =
⎧
⎨
⎩
pℓ if v = 0
1 − pℓ
q − 1
if v ∈ GF(q) {0}
(1)
where pℓ, for 0 < pℓ < 1, is the probability of having cj,i = 0.
The event cj,i ̸= 0 occurs with probability 1 − pℓ. We remark
that the average number of source packets involved in the
generation of a non-degenerate coded packet, i.e., the sparsity
of the code, can be controlled by tuning the value of pℓ, for
any ℓ = 1, . . . , L.
Since coding vectors are generated at random, there is the
possibility of generating coding vectors where each coding
coefficient is equal to 0. From a system implementation
p` = 1/q](https://image.slidesharecdn.com/uobsparse-151012141945-lva1-app6892/85/Sparse-Random-Network-Coding-for-Reliable-Multicast-Services-10-320.jpg)
![Markovian Model
13
5
rch
of
ich
on,
del
In
MC.
ing
u
ℓ,
s a
s
(u,ℓ)
kℓ
s
(u,ℓ)
kℓ−1
s
(u,ℓ)
1 s
(u,ℓ)
0
P
(u,ℓ)
kℓ,kℓ
P
(u,ℓ)
kℓ,kℓ−1
P
(u,ℓ)
kℓ−1,kℓ−1
P
(u,ℓ)
kℓ−1,kℓ−2 P
(u,ℓ)
2,1
P
(u,ℓ)
1,1
P
(u,ℓ)
1,0
P
(u,ℓ)
0,0
Fig. 2. State transition diagram for the AMC associated with user u and
message layer ℓ.
paper, owing to the lack of the exact expression of Pℓ,t, we
use (2) to approximate Pℓ,t, that is
Pℓ,t
∼= max pℓ,
1 − pℓ
q − 1
kℓ−t
. (3)
mes-
, kℓ.
t or
fect
The
MC
are
ave
rder
we
nted
Cu
1),
ent.
the
clearly not applicable to the sparse case, in contrast to (3).
It is worth mentioning that the considered approximation (3)
collapses to the exact expression of Pℓ,t and, hence, the
relation Pℓ,t = [max (pℓ, (1 − pℓ)/(q − 1))]kℓ−t
= qt
/qk
ℓ
holds, for pℓ = q−1
.
From (3), the transition probability matrix describing the
AMC associated with user u and message layer ℓ can be
derived by the following lemma.
Lemma 2.2: Assume layer ℓ is transmitted over a subchannel
which adopts the MCS with index m. The probability P
(u,ℓ)
i,j
of moving from state s
(u,ℓ)
i to state s
(u,ℓ)
j is
P
(u,ℓ)
i,j =
⎧
⎨
⎩
(1 − Pℓ,kℓ−i)[1 − pu(m)] if i − j = 1
Pℓ,kℓ−i[1 − pu(m)] + pu(m) if i = j
0 otherwise.
(4)
Proof: Since the user AMC is in state s
(u,ℓ)
i , user u
has collected kℓ − i linearly independent coded packets, i.e.,
User PER for a given MCS m
Unknown! We used an
upper-bound!](https://image.slidesharecdn.com/uobsparse-151012141945-lva1-app6892/85/Sparse-Random-Network-Coding-for-Reliable-Multicast-Services-13-320.jpg)
![Markovian Model
15
5
rch
of
ich
on,
del
In
MC.
ing
u
ℓ,
s a
s
(u,ℓ)
kℓ
s
(u,ℓ)
kℓ−1
s
(u,ℓ)
1 s
(u,ℓ)
0
P
(u,ℓ)
kℓ,kℓ
P
(u,ℓ)
kℓ,kℓ−1
P
(u,ℓ)
kℓ−1,kℓ−1
P
(u,ℓ)
kℓ−1,kℓ−2 P
(u,ℓ)
2,1
P
(u,ℓ)
1,1
P
(u,ℓ)
1,0
P
(u,ℓ)
0,0
Fig. 2. State transition diagram for the AMC associated with user u and
message layer ℓ.
paper, owing to the lack of the exact expression of Pℓ,t, we
use (2) to approximate Pℓ,t, that is
Pℓ,t
∼= max pℓ,
1 − pℓ
q − 1
kℓ−t
. (3)
as transient states [35]. The state transition diagram of th
resulting AMC can be represented as reported in Fig. 2.
From Lemma 2.2, it directly follows that th
(kℓ + 1) × (kℓ + 1) transition matrix T(u,ℓ)
describing
the AMC of user u and associated with layer ℓ has th
following structure in its canonical form [35]:
T(u,ℓ) .
=
1 0
R(u,ℓ)
Q(u,ℓ) , (5
where Q(u,ℓ)
is the kℓ × kℓ transition matrix modeling th
AMC process as long as it involves only transient states. Th
term R(u,ℓ)
is a column vector of kℓ elements which lists al
the probabilities of moving from a transient to the absorbing
(u,ℓ)
AMC transition
matrix
resulting AMC can be represented as reported in Fig. 2.
From Lemma 2.2, it directly follows that the
(kℓ + 1) × (kℓ + 1) transition matrix T(u,ℓ)
describing
the AMC of user u and associated with layer ℓ has the
following structure in its canonical form [35]:
T(u,ℓ) .
=
1 0
R(u,ℓ)
Q(u,ℓ) , (5)
where Q(u,ℓ)
is the kℓ × kℓ transition matrix modeling the
AMC process as long as it involves only transient states. The
term R(u,ℓ)
is a column vector of kℓ elements which lists all
the probabilities of moving from a transient to the absorbing
state. From [35, Theorem 3.2.4], let define matrix N(u,ℓ)
as
N(u,ℓ)
=
∞
t=0
Q(u,ℓ)
t
= I − Q(u,ℓ)
−1
. (6)
Element N
(u,ℓ)
i,j at the location (i, j) of matrix N(u,ℓ)
defines
Fundamental
matrix](https://image.slidesharecdn.com/uobsparse-151012141945-lva1-app6892/85/Sparse-Random-Network-Coding-for-Reliable-Multicast-Services-15-320.jpg)
![Markovian Model
๏ Why is the fundamental matrix so important? Its (i,j) element is
the avg. number of coded packet transmissions needed (to a
system started at the i-th state) to get to the j-th state.
๏ Hence, the avg number of transmissions needed to get to the
absorbing state (for a system started in the i-th state) is
16
i,j
the average number of coded packet transmissions required for
the process transition from state s
(u,ℓ)
i to state s
(u,ℓ)
j , where
both s
(u,ℓ)
i and s
(u,ℓ)
j are transient states. In particular, from
Lemma 2.2, the following theorem holds
Theorem 2.1 ([35, Theorem 3.3.5]): If the AMC is in the
transient state s
(u,ℓ)
i , the average number of coded packet
transmissions needed to get to state s
(u,ℓ)
0 is
τ
(u,ℓ)
i =
⎧
⎪⎨
⎪⎩
0 if i = 0
i
j=1
N
(u,ℓ)
i,j if i = 1, . . . , kℓ.
(7)
From (7) and Theorem 2.1, we prove the following corollaries.
Corollary 2.1: In the case of S-RLNC, the average number
τ
(u,ℓ)
S-RLNC of coded packets transmissions needed by user u to
recover the source message layer ℓ is τ
(u,ℓ)
= τ
(u,ℓ)
.
๏ In the non-systematic RNC we have
5, Theorem 3.3.5]): If the AMC is in the
)
, the average number of coded packet
d to get to state s
(u,ℓ)
0 is
0 if i = 0
i
j=1
N
(u,ℓ)
i,j if i = 1, . . . , kℓ.
(7)
em 2.1, we prove the following corollaries.
the case of S-RLNC, the average number
ackets transmissions needed by user u to
message layer ℓ is τ
(u,ℓ)
S-RLNC = τ
(u,ℓ)
kℓ
.
the source node transmits the very first
(u,ℓ)
simply a
value of
III. S
Amon
putation
consider
increase
per sou
remark
increase
resource](https://image.slidesharecdn.com/uobsparse-151012141945-lva1-app6892/85/Sparse-Random-Network-Coding-for-Reliable-Multicast-Services-16-320.jpg)
Sparse Random Network Coding for Reliable Multicast Services
- 1. Bristol, 12th October 2015 Sparse Random Network Coding for Reliable Multicast Services University of Bristol Andrea Tassi - [email protected] Communication Systems & Networks Group
- 2. Starting Point and Goals ๏ Point-to-Multipoint communications play a pivotal role in 4G/ 5G networks. We champion RLNC. ๏ A fundamental problem: the computational complexity of the RLNC decoder. The higher the number of decoding operations is, the more the user's computational overhead grows and, consequently, the faster the batteries of mobile devices drain. ๏ Layered service consists of a basic layer and multiple enhancement layers. Goals ๏ Efficient way to characterize the performance of users targeted by ultra-reliable layered multicast services ๏ Convex RA framework for minimizing the complexity of the RLNC decoder by jointly optimizing the transmission parameters and the sparsity of the code. 2
- 3. Index 1. System Model and RNC Background 2. Performance Analysis via Markov Chains 3. Resource Allocation for Sparse RLNC 4. Numerical Results 5. Concluding Remarks 3
- 4. 1. System Model and RNC Background
- 5. System Model ๏ One-hop wireless communication system composed of one source node and U users 5 UE 1 UE 3 UE 2 UE 4 UE U Source Node ˆB3 ˆB2 ˆB1 subch. 1 subch. 2 subch. 3 ๏ Each PtM layered service is delivered through C orthogonal broadcast erasure subchannels The same MCS Capacity of subch. 3 (no. of packets) ๏ Each subchannel delivers streams of (en)coded packets (according to a RLNC scheme).
- 6. 6 ๏ Encoding performed over each service layer independently from the others. ๏ The source node will linearly combine the data packets composing the l-th layer and will generate a stream of coded packets, where ๏ is a layered source message of K source packets, classified into L service layers x = {x1, . . . , xK} RNC in a Nutshell kl Coef:icients of the linear combination are selected over a :inite :ield of size q {xi}K` i=K` 1+1 yj = K`X i=K` 1+1 cj,i · xi k1 k2 k3 K3 = K K2 K1 x1 x2 . . .. . . xK Fig. 1. Layered source message, in the case of L = 3. the scope of the paper to provide analytical and optimization frameworks dealing with the compression strategy used to generate a scalable service. For these reasons, the proposed analysis has been made independent of the way service layers are generated and the nature of the adopted service scalability. As suggested in [12], [18], we model the transmitted service use rec tha SR an ide pa of sys is to sys
- 7. RNC in a Nutshell ๏ Let us refer to the user u and layer l. As user u successfully receives a coded packet, the corresponding coding vector is extracted and added, as a new row, into matrix . ๏ Assume u already received coded packets 7 Cu n` k` CuT(u,`) . = 1 0 R(u,`) Q(u,`) , (1) rows x colsn` k`n` k` 1 0 (u,`) Q(u,`) ,) . = 1 0 R(u,`) Q( c1 c2 cn` ...
- 8. RNC in a Nutshell ๏ When has rank equal to , the user can keep only the linearly independent rows and invert the matrix. 8 Cu n` k` Encoding Decoding Cu · xT ` = yT () C 1 u · yT ` = xT ` ๏ Given [1, 0] and [0, 1], is [2, 2] linearly independent? ✴ No, because 2[1, 0] + 2[0, 1] - [2, 2] = [0, 0] ๏ Given two lin. indep. vectors (a and b) in GF(q), how many vectors form span({a,b})? ✴ q2. For a = [1, 0], b = [0, 1] and q = 2, span({a,b}) = {[0, 0], [0, 1], [1, 0], [1, 1]]} ๏ Let us encode over a set of 5 inf. elements, if I collected 3 lin. indep. coding vectors, what is the prob. of collecting a new lin. dep. coding vec.? ✴ q3 / q5
- 9. 2. Performance Analysis via Markov Chains
- 10. The Coding Matrix ๏ Matrix is a random matrix over GF(q), where elements are independently and uniformly selected by the following prob. law 10 Cu ๏ If , all the GF(q) elements are equiprobable and things are nice and easy… otherwise, things get tricky! ๏ Since 1997, only 2 conference papers and 2 (+1 on Arxiv) journal papers deal with sparse random matrices. cupied vide an mission ice. of K essage. ber kℓ e MCS service e block (mℓ)⌉. source nd are cement ize the ill also parsity mized. the transmission of each layer shall meet a temporal constraint. The sparse versions of both the classic (S-RLNC) and systematic implementation of RLNC (S-SRLNC) are obtained as follows. Each component cj,i of a non-degenerate coding vector associated with source message layer ℓ is independently and identically distributed as follows [25]: Pr (cj,i = v) = ⎧ ⎨ ⎩ pℓ if v = 0 1 − pℓ q − 1 if v ∈ GF(q) {0} (1) where pℓ, for 0 < pℓ < 1, is the probability of having cj,i = 0. The event cj,i ̸= 0 occurs with probability 1 − pℓ. We remark that the average number of source packets involved in the generation of a non-degenerate coded packet, i.e., the sparsity of the code, can be controlled by tuning the value of pℓ, for any ℓ = 1, . . . , L. Since coding vectors are generated at random, there is the possibility of generating coding vectors where each coding coefficient is equal to 0. From a system implementation p` = 1/q
- 11. Should I Stay or Should I Go? ๏ Some actual performance value obtained by implementing a sparse RNC decoder in a Raspberry Pi Model B. ๏ If you can afford to wait, than sparsity is your best fit! 11 6 the the bing the (5) the The all bing as (6) pℓ Avg.Num.ofCod.Packets 0.5 0.6 0.7 0.8 0.9 1 5 15 25 35 45 55 65 75 85 95 105 S-RLNC, kℓ = 10 S-SRLNC, kℓ = 10 S-RLNC, kℓ = 70 S-SRLNC, kℓ = 70 pu = 0 pu = 0.1 (a) No. of coded packet transmissions pℓ Avg.Num.ofDecodingOp. 0.5 0.6 0.7 0.8 0.9 1 101 102 103 104 kℓ = 10 kℓ = 30 kℓ = 70 S-RLNC S-SRLNC 1030.8 µs 6310.0 µs 76.6 µs 757.3 µs 4972.6 µs 54.3 µs 352.6 µs 2868.2 µs 102.6 µs (b) No. of decoding operations Fig. 3. Average number of coded packet transmissions and decoding opera- tions, for q = 2. With regards the S-SRLNC scheme, the average number of decoding operations have been obtained by considering pu = 0.1. Proof: Assume that u collects kℓ −i out of kℓ systematic packets. Hence, matrix Cu consists of kℓ − i linearly inde- pendent rows and, hence, the user AMC is in state s (u,ℓ) .
- 12. Markovian Model ๏ Our chain models the process (seen from the perspective of the receiver) of building a full-rank coding matrix 12 Cu ๏ The chain is in state if linearly independent coded packets are still missing. ๏ That is an Absorbing Markov Chain (AMC)! 5 rch of ich on, del In MC. ing u s (u,ℓ) kℓ s (u,ℓ) kℓ−1 s (u,ℓ) 1 s (u,ℓ) 0 P (u,ℓ) kℓ,kℓ P (u,ℓ) kℓ,kℓ−1 P (u,ℓ) kℓ−1,kℓ−1 P (u,ℓ) kℓ−1,kℓ−2 P (u,ℓ) 2,1 P (u,ℓ) 1,1 P (u,ℓ) 1,0 P (u,ℓ) 0,0 Fig. 2. State transition diagram for the AMC associated with user u and message layer ℓ. paper, owing to the lack of the exact expression of Pℓ,t, we use (2) to approximate Pℓ,t, that is 1 − pℓ kℓ−t s (u,`) k` k`
- 13. Markovian Model 13 5 rch of ich on, del In MC. ing u ℓ, s a s (u,ℓ) kℓ s (u,ℓ) kℓ−1 s (u,ℓ) 1 s (u,ℓ) 0 P (u,ℓ) kℓ,kℓ P (u,ℓ) kℓ,kℓ−1 P (u,ℓ) kℓ−1,kℓ−1 P (u,ℓ) kℓ−1,kℓ−2 P (u,ℓ) 2,1 P (u,ℓ) 1,1 P (u,ℓ) 1,0 P (u,ℓ) 0,0 Fig. 2. State transition diagram for the AMC associated with user u and message layer ℓ. paper, owing to the lack of the exact expression of Pℓ,t, we use (2) to approximate Pℓ,t, that is Pℓ,t ∼= max pℓ, 1 − pℓ q − 1 kℓ−t . (3) mes- , kℓ. t or fect The MC are ave rder we nted Cu 1), ent. the clearly not applicable to the sparse case, in contrast to (3). It is worth mentioning that the considered approximation (3) collapses to the exact expression of Pℓ,t and, hence, the relation Pℓ,t = [max (pℓ, (1 − pℓ)/(q − 1))]kℓ−t = qt /qk ℓ holds, for pℓ = q−1 . From (3), the transition probability matrix describing the AMC associated with user u and message layer ℓ can be derived by the following lemma. Lemma 2.2: Assume layer ℓ is transmitted over a subchannel which adopts the MCS with index m. The probability P (u,ℓ) i,j of moving from state s (u,ℓ) i to state s (u,ℓ) j is P (u,ℓ) i,j = ⎧ ⎨ ⎩ (1 − Pℓ,kℓ−i)[1 − pu(m)] if i − j = 1 Pℓ,kℓ−i[1 − pu(m)] + pu(m) if i = j 0 otherwise. (4) Proof: Since the user AMC is in state s (u,ℓ) i , user u has collected kℓ − i linearly independent coded packets, i.e., User PER for a given MCS m Unknown! We used an upper-bound!
- 14. DoF Probability ๏ Assume that consists of elements. Assume that t out of t+1 rows are linearly independent. ๏ is the probability that is not full-rank and is upper- bounded as follows*: 14 Cu (t + 1) ⇥ k` P`,t Cu P`,t max ✓ p`, 1 p` q 1 ◆ k` t . * J. Blömer, R. Karp, and E. Welzl, “The Rank of Sparse Random Matrices Over Finite Fields,” Random Structures & Algorithms, vol. 10, no. 4, pp. 407–419, 1997. ๏ That bound is exact for , we havep` = 1/q P`,t = qt qk`
- 15. Markovian Model 15 5 rch of ich on, del In MC. ing u ℓ, s a s (u,ℓ) kℓ s (u,ℓ) kℓ−1 s (u,ℓ) 1 s (u,ℓ) 0 P (u,ℓ) kℓ,kℓ P (u,ℓ) kℓ,kℓ−1 P (u,ℓ) kℓ−1,kℓ−1 P (u,ℓ) kℓ−1,kℓ−2 P (u,ℓ) 2,1 P (u,ℓ) 1,1 P (u,ℓ) 1,0 P (u,ℓ) 0,0 Fig. 2. State transition diagram for the AMC associated with user u and message layer ℓ. paper, owing to the lack of the exact expression of Pℓ,t, we use (2) to approximate Pℓ,t, that is Pℓ,t ∼= max pℓ, 1 − pℓ q − 1 kℓ−t . (3) as transient states [35]. The state transition diagram of th resulting AMC can be represented as reported in Fig. 2. From Lemma 2.2, it directly follows that th (kℓ + 1) × (kℓ + 1) transition matrix T(u,ℓ) describing the AMC of user u and associated with layer ℓ has th following structure in its canonical form [35]: T(u,ℓ) . = 1 0 R(u,ℓ) Q(u,ℓ) , (5 where Q(u,ℓ) is the kℓ × kℓ transition matrix modeling th AMC process as long as it involves only transient states. Th term R(u,ℓ) is a column vector of kℓ elements which lists al the probabilities of moving from a transient to the absorbing (u,ℓ) AMC transition matrix resulting AMC can be represented as reported in Fig. 2. From Lemma 2.2, it directly follows that the (kℓ + 1) × (kℓ + 1) transition matrix T(u,ℓ) describing the AMC of user u and associated with layer ℓ has the following structure in its canonical form [35]: T(u,ℓ) . = 1 0 R(u,ℓ) Q(u,ℓ) , (5) where Q(u,ℓ) is the kℓ × kℓ transition matrix modeling the AMC process as long as it involves only transient states. The term R(u,ℓ) is a column vector of kℓ elements which lists all the probabilities of moving from a transient to the absorbing state. From [35, Theorem 3.2.4], let define matrix N(u,ℓ) as N(u,ℓ) = ∞ t=0 Q(u,ℓ) t = I − Q(u,ℓ) −1 . (6) Element N (u,ℓ) i,j at the location (i, j) of matrix N(u,ℓ) defines Fundamental matrix
- 16. Markovian Model ๏ Why is the fundamental matrix so important? Its (i,j) element is the avg. number of coded packet transmissions needed (to a system started at the i-th state) to get to the j-th state. ๏ Hence, the avg number of transmissions needed to get to the absorbing state (for a system started in the i-th state) is 16 i,j the average number of coded packet transmissions required for the process transition from state s (u,ℓ) i to state s (u,ℓ) j , where both s (u,ℓ) i and s (u,ℓ) j are transient states. In particular, from Lemma 2.2, the following theorem holds Theorem 2.1 ([35, Theorem 3.3.5]): If the AMC is in the transient state s (u,ℓ) i , the average number of coded packet transmissions needed to get to state s (u,ℓ) 0 is τ (u,ℓ) i = ⎧ ⎪⎨ ⎪⎩ 0 if i = 0 i j=1 N (u,ℓ) i,j if i = 1, . . . , kℓ. (7) From (7) and Theorem 2.1, we prove the following corollaries. Corollary 2.1: In the case of S-RLNC, the average number τ (u,ℓ) S-RLNC of coded packets transmissions needed by user u to recover the source message layer ℓ is τ (u,ℓ) = τ (u,ℓ) . ๏ In the non-systematic RNC we have 5, Theorem 3.3.5]): If the AMC is in the ) , the average number of coded packet d to get to state s (u,ℓ) 0 is 0 if i = 0 i j=1 N (u,ℓ) i,j if i = 1, . . . , kℓ. (7) em 2.1, we prove the following corollaries. the case of S-RLNC, the average number ackets transmissions needed by user u to message layer ℓ is τ (u,ℓ) S-RLNC = τ (u,ℓ) kℓ . the source node transmits the very first (u,ℓ) simply a value of III. S Amon putation consider increase per sou remark increase resource
- 17. 3. Resource Allocation for Sparse RLNC
- 18. Proposed RA Model ๏ The objective of the problem is to minimize the computational complexity of the decoding operations. ๏ The main constraints are those which impose an upper-limit to the avg. number of transmissions needed to allow a target number of users to recover a certain layer. 18 ST max p1,...,pL m1,...,mL kpk1 s.t. UX u=1 ⇣ ⌧ (u,`) S-RLNC ˆ⌧` ⌘ ˆU`, ` = 1, . . . , L q 1 p` < 1 ` = 1, . . . , L m` 2 {1, . . . , M} ` = 1, . . . , L The solution is not trivial… but we derived an analytical solution via referring to tools belonging to the convex optimization domain. The solution is safe!
- 19. Proposed RA Model 19 ST max p1,...,pL m1,...,mL kpk1 s.t. UX u=1 ⇣ ⌧ (u,`) S-RLNC ˆ⌧` ⌘ ˆU`, ` = 1, . . . , L q 1 p` < 1 ` = 1, . . . , L m` 2 {1, . . . , M} ` = 1, . . . , L ๏ The sum of the sparsity of each layer is maximized ๏ The no. of UEs experiencing at most the target avg. recovery delay shall be greater than or equal to a predetermined fraction ๏ RNC shall go sparse and not dense!
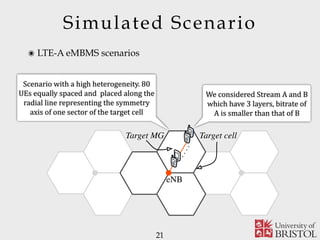
- 21. Target cellTarget MG eNB Scenario with a high heterogeneity. 80 UEs equally spaced and placed along the radial line representing the symmetry axis of one sector of the target cell Simulated Scenario 21 We considered Stream A and B which have 3 layers, bitrate of A is smaller than that of B ๏ LTE-A eMBMS scenarios
- 22. Distance (m) Avg.TransmissionFootprint 120 140 160 180 200 220 240 260 280 3000 500 1000 1500 1800 RLNC (q = 2) RLNC (q = 28 ) SRLNC (q = 2) SRLNC (q = 28 ) Layer 1 Layers 1 and 2 Layers 1, 2 and 3 200 205 210 215 220 225 230 280 330 380 430 480 530 ˆτ 2ˆτ 3ˆτ ˆU1 ˆU2 ˆU3 Stream A 22
- 23. Stream A 23 Distance (m) Avg.TransmissionFootprint 120 140 160 180 200 220 240 260 280 3000 500 1000 1500 1800 S-RLNC (q = 2) S-RLNC (q = 28 ) S-SRLNC (q = 2) S-SRLNC (q = 28 ) Layer 1 Layers 1 and 2 Layers 1, 2 and 3 ˆU1 ˆU2 ˆU3 ˆτ 2ˆτ 3ˆτ
- 24. Stream A 24 Distance (m) Avg.FootprintRatio 120 140 160 180 200 220 240 260 280 3001 3 5 7 9 11 S-RLNC/RLNC Pruned S-RLNC/RLNC S-SRLNC/SRLNC Pruned S-SRLNC/SRLNC Layer 1 Layers 1, 2 and 3 ˆU1 ˆU3
- 25. Stream A 25 Avg.NumberofOperations ˆτ (sec.) 0.2s 0.5s 1s 0.2s 0.5s 1s 0.2s 0.5s 1s 0.2s 0.5s 1s100 101 102 103 104 105 Layer 1 Layer 2 Layer 3 S-RLNC S-SRLNC 1.69·103 1.67·103 S-RLNC S-SRLNC 1.77·103 1.76·103 q = 2 q = 28 RLNC SRLNC RLNC SRLNC
- 26. Distance (m) Avg.TransmissionFootprintτ 120 140 160 180 200 220 240 260 280 3000 500 1000 1500 2000 2300 RNC (q = 2) RNC (q = 28 ) SRNC (q = 2) SRNC (q = 28 ) Layer 1 Layers 1 and 2 Layers 1, 2 and 3 Layers 1, 2, 3 and 4 200 205 210 215 220 225 230 323 373 423 473 523 573 623 ˆτ1 + ˆτ2 + ˆτ3 + ˆτ4 ˆU4 ˆU1 ˆU2 ˆU3 ˆτ1 ˆτ1 + ˆτ2 ˆτ1 + ˆτ2 + ˆτ3 Stream B 26
- 27. Stream B 27 Distance (m) Avg.TransmissionFootprintτ 120 140 160 180 200 220 240 260 280 3000 500 1000 1500 2000 2300 S-RNC (q = 2) S-RNC (q = 28 ) S-SRNC (q = 2) S-SRNC (q = 28 ) Layer 1 Layers 1 and 2 Layers 1, 2 and 3 Layers 1, 2, 3 and 4 ˆU4 ˆU1 ˆU2 ˆU3 ˆτ1 + ˆτ2 + ˆτ3 + ˆτ4 ˆτ1 ˆτ1 + ˆτ2 ˆτ1 + ˆτ2 + ˆτ3
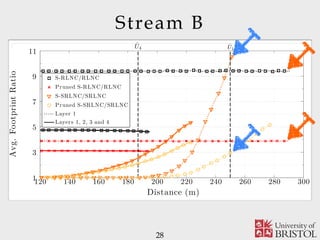
- 28. Stream B 28 Distance (m) Avg.FootprintRatio 120 140 160 180 200 220 240 260 280 3001 3 5 7 9 11 S-RLNC/RLNC Pruned S-RLNC/RLNC S-SRLNC/SRLNC Pruned S-SRLNC/SRLNC Layer 1 Layers 1, 2, 3 and 4 ˆU1 ˆU4
- 29. Stream B 29 Avg.NumberofOperations ˆτ (sec.) 0.2s 0.5s 1s 0.2s 0.5s 1s 0.2s 0.5s 1s 0.2s 0.5s 1s100 101 102 103 104 105 Layer 1 Layer 2 Layer 3 Layer 4 1.83·103 1.82·103 1.92·103 1.91·103 S-RLNC S-SRLNC S-RLNC S-SRLNC q = 2 q = 28 RLNC SRLNC RLNC SRLNC
- 31. Concluding Remarks 31 ๏ We addressed the issue of the complexity of a generic network coding decoder, in a multicast network scenario. ๏ We proposed a constrained convex resource allocation framework suitable for jointly optimizing both the MCS indexes and the code sparsity. ๏ The objective of the optimization model is that of minimizing the number of operations performed by a generic network coding decoder employing GE. ๏ The average transmission footprint is likely to increase as the sparsity of the code grows. However, this drawback is greatly reduced by simply avoiding the transmissions of all- zero coding vectors. ๏ The proposed optimization ensures a reduction in the average number of decoding operations of at least 57%.
- 32. Thank you for your attention For more information http://arxiv.org/abs/1411.5547 or http://goo.gl/Z4Y9YF A. Tassi, I. Chatzigeorgiou, and D. Vukobratović, “Resource Allocation Frameworks for Network-coded Layered Multimedia Multicast Services”, IEEE Journal on Selected Areas in Communications, Special Issue on “Fundamental Approaches to Network Coding in Wireless Communication Systems”, in press.
- 33. Bristol, 12th October 2015 Sparse Random Network Coding for Reliable Multicast Services University of Bristol Andrea Tassi - [email protected] Communication Systems & Networks Group