[Swift] Data Structure - Binary Tree

SWIFT
Data Structure -
Binary Tree
Bill Kim(김정훈) | ibillkim@gmail.com

목차
•Binary Tree
•Uses
•Traversal
•Implementation
•References

Binary Tree
이진 트리(Binary Tree)는 한 노드가 최대 2개의 자식 노드만 가질
수 있는 트리를 말합니다.
공백 노드는 허용하며 이진 트리의 모든 서브 트리도 모두 이진 트
리 형태를 취해야 합니다.
좌, 우로 구분하여 자식 노드를 가지고 있습니다.

Binary Tree
이진 트리(Binary Tree)는 트리의 모양에 따라서 아래와 같은 형
태로 분류될 수 있습니다.

Uses
이진 트리(Binary Tree)를 사용하여 보편적으로 활용되는 트리로
는 아래와 같은 것들이 있습니다.
이진 검색 트리(Binary Search Tree, BST) :
이진 트리 구조를 가진 형태의 트리로서 자료의 검색, 삭제, 삽입이
효율적으로 이루어질 수 있도록 한 트리
AVL 트리(Adelson-Velskii and Landis’s Tree) :
한 노드를 중심으로 좌우 부분의 트리 높이의 차가 1 이하가 되도록
하는 이진 탐색 트리, 가장 초기에 나온 균형 잡힌 이진 탐색 트리
B 트리(B-Tree, Balanced Tree) :
다수의 키를 가진 노드로 구성되어 다방향 탐색이 가능한 트리, 2-
3 트리의 확장된 형태로서 데이터베이스 및 파일 시스템 등에서 활
용되고 있습니다.

Traversal
이진 트리(Binary Tree) 내에 있는 데이터를 접근하는 방법은 아
래와 같이 3가지 방식이 있습니다.
1. 전위 순회(Preorder Traversal) : 루트(현재) 노드 -> 왼쪽 자
식 노드-> 오른쪽 자식 노드를 재귀적으로 방문하는 방식
2. 중위 순회(Inorder Traversal) : 왼쪽 자식 노드-> 오른쪽 자식
노드 -> 루트 노드를 재귀적으로 방문하는 방식
3. 후위 순회(Postorder Traversal) : 왼쪽 자식 노드-> 오른쪽
자식 노드 -> 루트 노드를 재귀적으로 방문하는 방식

Traversal
전위 순회(Preorder Traversal)
루트(현재) 노드 -> 왼쪽 자식 노드-> 오른쪽 자식 노드

Traversal
중위 순회(Inorder Traversal)
왼쪽 자식 노드-> 오른쪽 자식 노드 -> 루트 노드

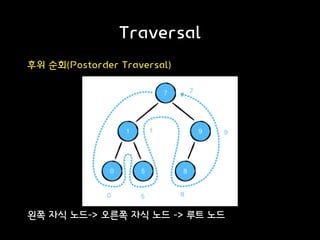
Traversal
후위 순회(Postorder Traversal)
왼쪽 자식 노드-> 오른쪽 자식 노드 -> 루트 노드

Features
Binary Tree의 특징을 살펴보면 아래와 같습니다.
- 모든 노드가 최대 2개의 자식 노드를 가질 수 있는 트리
- 좌측과 우측으로 자식 노드를 구분
- 방문 순서에 따라서 전위, 중위, 후위 순회 방식이 있음
- 이진 트리는 많은 트리 구조와 알고리즘 등에 기초 역할을 수행

Implementation
Swift를 활용하여 가장 기본적인 Binary Tree를 구현해보겠습니
다. 본 강의에서는 enum을 활용한 방식과 일반 class 방식 두 가지
를 살펴보겠습니다.
우선 필요한 메소드는 아래와 같습니다.
- init : 이진 트리를 초기화하고 값을 생성해주는 함수
- traversePreOrder : 전위 순회를 실행하는 함수
- traverseInOrder : 특정 트리를 검색
- traversePostOrder : 특정 트리를 검색

Implementation
// recursive enum 은 indirect 키워드 적어줘야함
public indirect enum BinaryTree<T : Comparable> {
case node(BinaryTree<T>, T, BinaryTree<T>)
case empty
public var count: Int {
switch self {
case let .node(left, _, right):
return left.count + 1 + right.count
case .empty:
return 0
}
}
}
extension BinaryTree: CustomStringConvertible {
public var description: String {
switch self {
case let .node(left, value, right):
return "value: (value), left = [(left.description)], right = [
(right.description)]"
case .empty:
return ""
}
}
}

Implementation
extension BinaryTree {
public func traverseInOrder(process: (T) -> Void) {
// 같은 BinaryTree만 가능하도록
if case let .node(left, value, right) = self {
left.traverseInOrder(process: process)
process(value)
right.traverseInOrder(process: process)
}
}
public func traversePreOrder(process: (T) -> Void) {
process(value)
left.traversePreOrder(process: process)
right.traversePreOrder(process: process)
}
}
public func traversePostOrder(process: (T) -> Void) {
left.traversePostOrder(process: process)
right.traversePostOrder(process: process)
process(value)
}
}
}

Implementation
// leaf nodes
let node5 = BinaryTree.node(.empty, "5", .empty)
let nodeA = BinaryTree.node(.empty, "a", .empty)
let nodeB = BinaryTree.node(.empty, "b", .empty)
// intermediate nodes on the left
let aMinus10 = BinaryTree.node(nodeA, "-", node10)
let timesLeft = BinaryTree.node(node5, "*", aMinus10)
// intermediate nodes on the right
let minus4 = BinaryTree.node(.empty, "-", node4)
let divide3andB = BinaryTree.node(node3, "/", nodeB)
let timesRight = BinaryTree.node(minus4, "*", divide3andB)
// root node
let tree = BinaryTree.node(timesLeft, "+", timesRight)

Implementation
print(tree.traversePreOrder(process: { _ in }))
// ["+", "*", "5", "-", "a", "10", "*", "-", "4", "/", "3", "b"]
print(tree.traverseInOrder(process: { _ in }))
// ["5", "*", "a", "-", "10", "+", "-", "4", "*", "3", "/", "b"]
print(tree.traversePostOrder(process: { _ in }))
// ["5", "a", "10", "-", "*", "4", "-", "3", "b", "/", "*", "+"]

Implementation
public class BinaryNode<T> {
public var value: T
public var leftChild: BinaryNode?
public var rightChild: BinaryNode?
public init(value: T) {
self.value = value
}
public func traversePreOrder(visit: (T) -> Void) -> [T] {
var results = [T]()
results.append(value)
visit(value)
if leftChild != nil { results += leftChild!.traversePreOrder(visit: visit) }
if rightChild != nil { results += rightChild!.traversePreOrder(visit: visit) }
return results
}
public func traverseInOrder(visit: (T) -> Void) -> [T] {
var results = [T]()
if leftChild != nil { results += leftChild!.traverseInOrder(visit: visit) }
visit(value)
if rightChild != nil { results += rightChild!.traverseInOrder(visit: visit) }
return results
}
public func traversePostOrder(visit: (T) -> Void) -> [T] {
var results = [T]()
if leftChild != nil { results += leftChild!.traversePostOrder(visit: visit) }
if rightChild != nil { results += rightChild!.traversePostOrder(visit: visit) }
visit(value)
return results
}
}

Implementation
extension BinaryNode: CustomStringConvertible {
public var description: String {
return diagram(for: self)
}
private func diagram(for node: BinaryNode?,
_ top: String = "",
_ root: String = "",
_ bottom: String = "") -> String {
guard let node = node else {
return root + "niln"
}
if node.leftChild == nil && node.rightChild == nil {
return root + "(node.value)n"
}
return diagram(for: node.rightChild, top + " ", top + "┌──", top + "│ ")
+ root + "(node.value)n"
+ diagram(for: node.leftChild, bottom + "│ ", bottom + "└──", bottom
+ " ")
}
}

Implementation
let root = BinaryNode(value: 7)
let zero = BinaryNode(value: 0)
let one = BinaryNode(value: 1)
let five = BinaryNode(value: 5)
let eight = BinaryNode(value: 8)
let nine = BinaryNode(value: 9)
root.leftChild = one
one.leftChild = zero
one.rightChild = five
root.rightChild = nine
nine.leftChild = eight
print(root)
// ┌──nil
// ┌──9
// │ └──8
// 7
// │ ┌──5
// └──1
// └──0

Implementation
print(root.traversePreOrder(visit: { _ in }))
// [7, 1, 0, 5, 9, 8]
print(root.traverseInOrder(visit: { _ in }))
// [0, 1, 5, 7, 8, 9]
print(root.traversePostOrder(visit: { _ in }))
// [0, 5, 1, 8, 9, 7]

References
[1] 스위프트: 이진 트리: #BinaryTree: #자료구조: #탐색: #in-
order: #pre-order: #post-order : https://the-brain-of-
sic2.tistory.com/25
[2] Swift, Data Structure, Binary Trees : https://
devmjun.github.io/archive/BinaryTree
[3] [Swift 자료구조 ch13] Tree 의 구현 : https://
kor45cw.tistory.com/258
[4] Swift, Data Structure, Binary Search Trees : https://
devmjun.github.io/archive/BinarySearchTree
[5] [Swift] Binary Search Tree ( 이진 탐색 트리 ) 를 Swift로 구
현해보자 + search / insert / delete : https://
eunjin3786.tistory.com/17

References
[6] [Swift] 이진 트리 : https://milyo-codingstories.tistory.com/54
[7] [Swift] 이진 탐색 트리 : https://milyo-codingstories.tistory.com/
60
[8] Swift 4에서 이진 트리를 그리는 방법은 무엇입니까? : https://
www.python2.net/questions-445468.htm
[9] [구조] 이진 트리(Binary Tree) : http://blog.naver.com/
PostView.nhn?
blogId=yeop9657&logNo=220897908545&parentCategoryNo=&c
ategoryNo=119&viewDate=&isShowPopularPosts=false&from=p
ostView
[10] Binary Tree : https://miyon2.gitbooks.io/til/
[Data_structure]/[DS]Binary_Tree.html

[Swift] Data Structure - Binary Tree

Recommended

More Related Content

What's hot (20)

Similar to [Swift] Data Structure - Binary Tree (17)

More from Bill Kim (20)

[Swift] Data Structure - Binary Tree