Disparity Estimation by a Real Time Approximation Algorithm

Md. Abdul Mannan Mondal & Md. Haider Ali
International Journal of Image Processing (IJIP), Volume (10) : Issue (3) : 2016 126
Disparity Estimation by a Real Time Approximation Algorithm
Md. Abdul Mannan Mondal mannan_mondal@yahoo.com
Department of Computer Science and Engineering
University of Dhaka
Dhaka, 1000, Bangladesh
Md. Haider Ali haider@du.ac.bd
Department of Computer Science and Engineering
University of Dhaka
Dhaka, 1000, Bangladesh
Abstract
This paper presents an approximation real time algorithm for estimating the disparity of the stereo
images. The approximation is achieved by shrinking the left and right of original images.
According to this method (i ) left and right images have been shrinked three times,(ii) the disparity
image is computed from the shrinked left and right images to reconstruct the disparity image and
extrapolate the disparity image to retrieve the original image size. The computational time of
proposed algorithm is less than the existing methods, approximately real time and requires less
memory space. This method is applied on the standard stereo images and the results show that it
can easily reduce the computational time of about 76.34 % with no appreciable degradation of
accuracy.
Keywords: Stereo Matching, Quantization, Approximation, Stereo Corresponding, Disparity, Sum
of Absolute Differences, Normalized Correlation.
1. INTRODUCTION
The difference in the coordinates of the corresponding pixels is known as disparity, which is
inversely proportional to the distance of the object from the camera. Stereo correspondence is a
common tool in computer or robot vision, essential for determining three-dimensional depth
information of object using a pair of left and right images from a stereo camera system. For of a
pixel in the left image, its correspondence has to be searched in the right image based on the
epipolar line and maximum disparity. Stereo correspondence or disparity is conventionally
determined of matching windows of pixels by using Sum of Square Differences (SSD), Sum of
Absolute Difference (SAD) or normalized correlation techniques.
Window-based stereo correspondence estimation technique is widely used due to its efficiency
and ease of implementation. However, there is a well-known problem in the selection of an
appropriate size and shape of window [1, 2]. If the window is small and does not cover enough
intensity variation, it gives erroneous result due to low signal to noise ratio. If, on the other hand,
the window is large, it includes a region where the disparity varies or discontinuity of disparity
happens, then the result becomes erroneous due to different projective distortions in the left and
right images. Pixels that are close to a disparity discontinuity require windows of different shapes
to avoid crossing the discontinuity. Therefore, different pixels in an image require windows of
different shapes and sizes.
To overcome this problem, many researchers proposed adaptive window techniques using
windows of different shapes and sizes [3-7]. In adaptive window technique, it requires comparing
the window costs for different window sizes and shapes, so the computation time is relatively

higher than that of fixed window based technique. For example, in the references 6 and 7 the
authors used a direct search over several window shapes to find the one that gives the best
window cost. Beside gray scale stereo images, the use of color stereo images brings a
substantial gain in accuracy with the expense of computation time [8].
The better classifications have presented by Scharstein and Szeliski[11] and many new methods
have been proposed here. Primarily matching algorithms can be classified with respect to spare
output and dense output. Feature based methods that based on segments or edges between
stereo images result sparse output. Such type of output has the limitations both speed and
accuracy due to their disadvantages causes it dreadful for many applications. Dense matching
algorithms are divided into local and global ones.
Local methods are also known as area based stereo matching that can perform better speed
compare to global methods. According to this, disparity is being calculated at a point in a fixed
window. Global methods are also known as intensity or energy based stereo matching that can
perform better accuracy compare to local methods. According to this method, the global cost
function is reduced as minimum as possible. This cost function synthesizes image data and
smoothness terms. Besides these some algorithms are not fallen into above mentioned two
categories. Recently, neural adaptive stereo matching [13] are done by trained neural networks
based on window size and shape. One dimensional cellular automation filter [16] makes the
algorithm more adaptive to each window. Almost real-time performance method is reported in [15]
presented by Yoon. It uses SAD method and a left-right consistency check. This method is able
to find out the errors in the problematic regions are reduced using different sized correlation
windows. Accordingly, a median filter is used in order to interpolate the results. The algorithm can
process 7 fps for 320×240 pixels images and 32 disparity levels. The result has been justified by
using an Intel Pentium 4 at 2.66GHz Processor.
The uses of Cellular Automata (CA) are presented in [16].This work presents architecture for real-
time extraction of disparity maps. The proposed method can process 1Mpixels image pairs at
more than 40 fps. The key idea behind the algorithm relies on matching pixels of each scan-line
using a one-dimensional window and the SAD matching cost. According to the method a pre-
processing mean filtering step and a post-processing CA based filtering ones are employed. CA’s
are models of physical systems, where space and time are discrete and interactions are local.
They can easily handle complicated boundary and initial conditions. In CA analysis, physical
processes and systems are described by a cell array and a local rule which defines the new state
of a cell depending on the states of its neighbors.
A window-based method is presented in [18] that use different support-weights. The support-
weights of the pixels in a given support window are adjusted based on geometric proximity and
color similarity to reduce the image ambiguity [19]. The running time for the Tsukuba image pair
with a 35×35 pixels support window is about 0.016 fps on an AMD 2700+ processor. The error
ratio is 1.29%, 0.97%, 0.99%, and 1.13% for the Tsukuba, Sawtooth, Venus and Map image sets
respectively. The experimental results can be further improved through a left-right consistency
checking.
In a global algorithm, the disparity of every single pixel is calculated by taking into consideration
the whole image. Global optimization methodologies involve segmentation of the input images
according to their colors. The accuracy of the global methods is very high but the computational
costs are also high due to repetitive comparison.
The research work presented in [18] based on unified framework that supports the fusion of any
partial knowledge such as matching features and surfaces about disparities. Accordingly, it
combines the results of edge, corner and dense stereo matching algorithm to act as a guide
points to the standard dynamic programming method. The result is a fully automatic dense stereo
system with up to four times faster running speed and greater accuracy compared to results
obtained by the sole use of dynamic programming.

A method based on the Bayesian estimation theory with a prior Markov Random Fields model for
the assigned disparities is described in [20]. According to this method, the continuity, coherence,
occlusion constraints and the adjacency principal are taken into considerations. The optimal
estimator is computed using a Gauss-Markov random field model for the corresponding posterior
marginal, which results in a diffusion process in the probability space. The results are accurate
but the algorithm is not suitable for real-time applications, since it needs a few minutes to process
a 256×255 stereo pair with up to 32 disparity levels, on an Intel Pentium III running at 450 MHz.
Image color segmentation is reported in [21]. By this method disparity map is estimated using an
adapting window based technique. The segments are combined in larger layers iteratively. A
global cost function is used to optimize the segments to layers. The quality of the disparity map is
measured by warping the reference image to the second view and comparing it with the real
image and calculating the color dissimilarity. For the 384×288 pixel Tsukuba and the 434×383
pixel Venus test set, the algorithm produces results at 0.05 fps rate and needed 20 s to produce
results. For the 450×375 pixel Teddy image pair, the running speed decreased to 0.01 fps due to
the increased scene complexity. Running speeds refer to an Intel Pentium 4 2.0GHz processor.
The root mean square error obtained is 0.73 for the Tsukuba, 0.31 for the Venus and 1.07 for the
Teddy image pair.
It is aimed that this approximation method will be useful in such situations for speedy
determination of dense disparity.
2. APPROXIMATION METHOD
In the proposed approximation method, experimental left and right images has been shrinked
three times with a view to reduce the computational time and searching area of given standard
images. The SSD method has been applied for all candidate pixels in the right image within the
searching range. To reconstruct the original disparity image, extrapolation is applied on the
experimentally estimated disparity image. Various methods can be used for shrinking the left and
right images for extrapolation. Proposed method uses the pixel quantization technique for
extrapolation. The Figure 1 shows the hierarchical schematic diagram of the approximation
method for disparity estimation.
FIGURE 1: Hierarchical schematic diagram of approximation method.
Right Image
Shrinked Right
Image
Shrinked Left
Image
Experimental
estimated
disparity
Image
Extrapolated
disparity
Image
Left Image
Dispa
rity
Imag
e

3. SHRINKING PROCESS
Shrinking process can be viewed as the technique of quantization under a part of the
approximation method. Window averaging method is used to shrink the left and right images in
the proposed method. The key idea behind the technique is that nine pixels(consider the first
window of right image) of original image are quantized to single pixel in shrinked image of Figure
2.This single pixel is marked by dark area in Figure 2 at last portion and it demonstrates all
things on behalf of nine pixels of original image. Next nine pixels of original image are quantized
to single pixel following the same manner but it will be allocated in the second coordinate of the
shrinked image. The consecutive nine pixels of original image relocated in the third coordinate of
the shrinked image and so on. The original image size was [m-1] × [n-1].After quantization the
image size has been reduced to {[m-1]/3 × [n-1]/3}. As the experimental images are shrinked two
dimensionally i.e. nine times [3×3], so the computational costs are also reduced nine times
compared to the traditional methods.
The total prefecture of our proposed method is represented by the flow chart of Figure-3. Actually,
this method involved three looping steps which are quantization, disparity selection and
extrapolation those are shown separately in the flow chart of Figure 3.
FIGURE 2: Shrinking Process.
Quantize
window
Original
image
0 1 2……… n-1
0
1
.
.
.
.
.
.
m-1
0
1
.
.
(m-1)/3
Shrinked image
0 1……… (n-1)/3

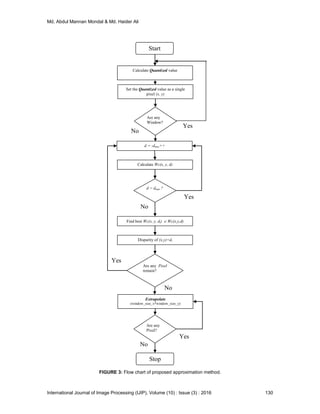
FIGURE 3: Flow chart of proposed approximation method.
Start
Calculate Quantized value
Set the Quantized value as a single
pixel (x, y)
Are any
Window?
Calculate Wc(x, y, d)
d = dmax ?
Disparity of (x,y)=di
Find best Wc(x, y, di)  Wc(x,y,d)
Are any Pixel
remain?
Extrapolate
(window_size_x*window_size_y)
Are any
Pixel?
Stop
d = -dmax++
Yes
No
Yes
Yes
Yes
No
No
No

4. APPROXIMATION ALGORITHM EMPLOYED FOR DISPARITY
ESTIMATION
1. for each window
i) Calculate the quantization value
ii) Set quantized value as a single pixel (x,y)
end [ end of the quantization process]
2. for each pixel (x,y)
for d= -dmax to +dmax do
Calculate Wc(x,y,d)
end [ end of the searching range]
find best Wc(x,y,di)  Wc(x,y,d)
disparity of (x,y)=di
3. for each pixel (x,y)
Extrapolate (window_size_x *window_size_y) times
end [ end of the extrapolation process]
5. EXPERIMENTAL RESULTS
The accuracy and speed of this algorithm has been justified over some standard stereo images
(Tsukuba Head). The images are provided by the computer Vision and Image Media Laboratory,
University of Tsukuba, Japan. Experiments are performed on a corei5 3.2 GHz processor PC with
4 GB RAM. The algorithm has been implemented using Visual C++ programming language.
Table 1 illustrates the summary of comparison between window based traditional method and
proposed approximation method. The computational time using a corei5 3.2 GHz processor
without any threshold for window sizes 33 pixels is shown here. From this table, it reveals that
for a window of size 33 is applied for the disparity calculation of both methods, proposed
approximation method reduced 76.34 % of computational time. The following Figure 4 and Figure
5 shows the Tskuba Head of left and right images view. The Figure 6 and Figure 7shows the
shrinked images of left and right images respectively after applying quantization technique. Figure
8 shows the disparity image that is experimentally estimated from left and right image applying
approximation method. The Figure 9 shows the extrapolated image of experimental disparity
image. Experimental disparity images of Figure 8 and Figure 9 are histogram equalized for
visualization purpose.
FIGURE 4: Left image 384 X 288.

FIGURE 5: Right image 384 X 288.
FIGURE 6: Shrinked left image 128 X 96.
FIGURE 7: Shrinked Right image 128 X 96.
FIGURE 8: Experimentally estimated disparity image 116 X 84.
FIGURE 9: Extrapolated image 348 X 252.
The size of the left and right image is (width × height) = (384 × 288) pixels, the shrinked image

size is (width × height) = (128 × 96) pixels, disparity image size is (width × height) = (116 × 84)
pixels and extrapolated image size is (width × height) = (348 ×252) pixels.
Applying
Methods
Window
size
Computational time
(in second)
Computational
time reduction (%)
Window based traditional
method
3 ×3 0.93
76.34
Approximation method
3 × 3 0.22
TABLE 1: Computational time reduction (%) compare to Window based method.
From the above experimental results although the computational time reduction has been
improved but some accuracy of ground truth image has been degraded(FIGURE 8 and FIGURE
9).This happened in shrinking process because 9 pixels are quantized at a single pixel. So eight
(8) pixels might lose their some intensity attributes. Beside this some accuracy has been lost
during the extrapolation process.
6. CONCLUSIONS
Experimental results confirm that we can easily reduce the computation time of about 76.34 %
with no appreciable degradation of accuracy. We believe that this approximation method will be
useful for many applications where a very fast estimation of dense disparities is essential.
7. FURTHER IMPROVEMENT
For further improvement one can improve the accuracy of the disparity image. Different method
can be used for shrinking the given left and right image. The accuracy might be retrieved by
proper mapping of each pixel during the reconstruction of dense disparity.
8. ACKNOWLEDGEMENT
We thank Dr. Y. Ohta and Dr. Y. Nakamura from the Computer Vision and Image Media
Laboratory, University of Tsukuba, Japan for providing the stereo images with the dense ground
truth.
9. REFERENCES
[1] S. T. Barnard and M. A. Fischler, “Stereo vision,” in Encyclopedia of Artificial Intelligence,
(John Wiley, New York, 1987), pp. 1083-1090.
[2] W. Hoff and N. Ahuja, “Surfaces from stereo: Integrating feature matching, disparity
estimation and contour detection,” IEEE Trans. Pattern Anal. Machine Intell., vol. 11, no. 2,
pp.121-136, (1989).
[3] T. Kanade and M. Okutomi, “A stereo matching algorithm with an adaptive window: Theory
and experiment,” IEEE Trans. Pattern Anal. Machine Intell., vol. 16, no. 9, (1994).
[4] Olga Veksler, “Stereo matching by compact windows via minimum ratio cycle,” in
Proceedings of the IEEE International Conference on Computer Vision (ICCV 2001),pp.
540-547.
[5] Mohammad Shorif Uddin, Tadayoshi Shioyama, Mozammel Hoque Chowdhury, Md. Abdul
Mannan Mondal, “Fast Window Based Approach For Stereo Matching”, Journal of Science,
Jahangirnagar University, vol. 27, pp: 145-154, June 2004.

[6] S. S. Intille and A. F. Bobick, “Disparity-space images and large occlusion stereo,” in
Proceedings of the European Conference on Computer Vision (ECCV 1994), pp. 179-186.
[7] A. Fusiello and V. Roberto, “Efficient stereo with multiple windowing,” in Proceedings of the
IEEE Conference on Computer Vision and Pattern Recognition (ICVPR 1997), pp. 858-863.
[8] K. Muhlmann, D. Maier, J. Hesser, R. Manner, “Calculating dense disparity maps from color
stereo images, an efficient implementation,” in Proceedings of the IEEE Conference on
Computer Vision and Pattern Recognition (ICVPR 2001), pp. 30-36.
[9] Mohammad Shorif Uddin, “Stereo correspondence estimation using window- based methods
by a fast algorithm” journal of electronics and computer science, vol. 4, June 2003, pp. 5-11.
[10] Md. Abdul Mannan Mondal, Md.Al-Amin Bhuiyan “Disparity Estimation By A Two-Stage
Approximation Real Time Algorithm” The International Management and Technology
Conference (IMT), pp: 12-17, 8 - 10 December 2004, Orlando, Florida 32819, USA.
[11] D.Schartein ,R.Szeliski, “ A taxonomy and evaluation of dense two frame stereo
correspondence algorithms”, IJCV 7, 1/3,2002.
[12] Lugi Di Stefano,Massimiliano Marchionni, Stefano Mattoccia, “A fast Area Based Stereo
Matching Algorithm” , Image and vision Computing 22,pp.983-1005,2004.
[13] Elisabetta Binaghi, Ignazio Gallo, Giuseppe Marino, Mario Raspanti, “Neural adaptive stereo
matching”, Pattern Recognition Letters 25,pp. 1743-1758,2004.
[14] Abijit S.Ogale and Yiannis Aloimonos , “Shape and the Stereo Correspondence Problem”,
IJCV 65,3,pp.147-167,2005.
[15] Sukjune Yoon,Sung-Kee Park, Sungehul Kang, Yoon Keun Kwak, “Fast correlation –based
stereo matching with the reduction of systematic errors”, Pattern Recognition Letters 26, pp.
2221-2231,2005.
[16] L. Kotoulas, A. Gasteratos,G.Ch.Sirakoulis , C. Georoulas, and I. Andreadis, “Enhancement
of Fast Acquired Disparity Maps using a 1-D Cellular Automation Filter”, proceedings of the
fifth IASTED International Conference on Visualization, Imaging and Image Processing,
Benidorn, Spain,September 7-9,2005.
[17] Kuk-Jin Yoon and In So Kweon, “Adaptive Support –Weight Approach for Correspondence
Search”, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol.28,no. 4, April
2006.
[18] P.H.S. Torra, A. Criminisi, “Dense stereo using pivoted dynamic programming”, Image and
Vision Computing 22, pp. 795-806, 2004.
[19] Lazaros Nalpantidis,Georgios Ch. Sirakoulis and Antonios Gasteratos, “Rieview of stereo
matching algorithms for 3D vision”, 16th International Symposium on Measurement and
Control in Robotics ISMCR, pp.116-124,2007.
[20] Salvador Gutierrez,Jose Luis Marroquin, “Robust approach for disparity estimation in stereo
vision”, Image and Vision Computing 22, pp. 183-195, 2004.
[21] Michael Bleyer, Margrit Gelautz, “ A layered stereo matching algorithm using image
segmentation and global visibility constraints”, ISPRS Journal of Photogrammetry and
Remote Sensing 59,pp.128-150,2005.

Disparity Estimation by a Real Time Approximation Algorithm

More Related Content

What's hot (18)

Similar to Disparity Estimation by a Real Time Approximation Algorithm (20)

Recently uploaded (20)

Disparity Estimation by a Real Time Approximation Algorithm