Tutorial of topological_data_analysis_part_1(basic)
8 likes7,999 views
This document provides an overview of topological data analysis (TDA) concepts, including: - Simplicial complexes which represent topological spaces and holes of different dimensions - Persistent homology which tracks the appearance and disappearance of holes over different scales - Applications of TDA concepts like using persistent homology to analyze protein compressibility.
![Homology group
34
Homology groups
The qth
Homology Group Hq is defined as Hq = Ker@q/Im@q+1
= {z + Im@q+1 | z 2 Ker@q } = {[z]|z 2 Ker@q}
Divided in groups with operator [z] + [z’] = [z + z’]
Betti Numbers
The qth
Betti Number is defined as the dimension of Hq
bq = dim(Hq)
H0(K): connected component H1(K): ring H2(K): cavity
3 - Definition of Holes](https://image.slidesharecdn.com/tutorialoftopologicaldataanalysispartibasic-160415071715/85/Tutorial-of-topological_data_analysis_part_1-basic-34-320.jpg)
![Persistent Homology
39
✤ Z2 - vector space
✤ Z2[x] - graded module
✤ Inclusion map
✤ is a free Z2[x] module with the baseCk(K)
Persistent homology Slide source: http://www2.math.kyushu-u.ac.jp/~hiraoka/protein_homology.pdf](https://image.slidesharecdn.com/tutorialoftopologicaldataanalysispartibasic-160415071715/85/Tutorial-of-topological_data_analysis_part_1-basic-39-320.jpg)
![Persistent Homology
41
✤ From the structure theorem of Z2[x] (PID)
✤ Persistent interval
✤ Persistent diagram
Ii(b): inf of Ii, Ii(d): sup of Ii
Persistent homology Slide source: http://www2.math.kyushu-u.ac.jp/~hiraoka/protein_homology.pdf](https://image.slidesharecdn.com/tutorialoftopologicaldataanalysispartibasic-160415071715/85/Tutorial-of-topological_data_analysis_part_1-basic-41-320.jpg)
Tutorial of topological_data_analysis_part_1(basic)
- 1. Tutorial of Topological Data Analysis Tran Quoc Hoan @k09hthaduonght.wordpress.com/ Hasegawa lab., Tokyo The University of Tokyo Part I - Basic Concepts
- 2. My TDA = Topology Data Analysis ’s road TDA Road 2 Part I - Basic concepts & applications Part II - Advanced computation Part III - Mapper Algorithm Part V - Applications in… Part VI - Applications in… Part IV - Software Roadmap He is following me
- 3. Outline TDA - Basic Concepts 3 1. Topology and holes 3. Definition of holes 5. Some of applications 2. Simplicial complexes 4. Persistent homology
- 4. Outline TDA - Basic Concepts 4 1. Topology and holes 5. Some of applications 2. Simplicial complexes 4. Persistent homology 3. Definition of holes
- 5. Topology I - Topology and Holes 5 The properties of space that are preserved under continuous deformations, such as stretching and bending, but not tearing or gluing ⇠= ⇠= ⇠= ⇠= ⇠= ⇠= ⇠=
- 6. Invariant 6 Question: what are invariant things in topology? ⇠= ⇠= ⇠= ⇠= ⇠= ⇠= ⇠= Connected Component Ring Cavity 1 0 0 2 0 0 1 1 0 1 10 Number of I - Topology and Holes
- 7. Holes and dimension 7 Topology: consider the continuous deformation under the same dimensional hole ✤ Concern to forming of shape: connected component, ring, cavity • 0-dimensional “hole” = connected component • 1-dimensional “hole” = ring • 2-dimensional “hole” = cavity How to define “hole”? Use “algebraic” Homology group I - Topology and Holes
- 8. Homology group 8 ✤ For geometric object X, homology Hl satisfied: k0 : number of connected components k1 : number of rings k2 : number of cavities kq : number of q-dimensional holes Betti-numbers I - Topology and Holes Image source: http://www2.math.kyushu-u.ac.jp/~hiraoka/protein_homology.pdf
- 9. Outline TDA - Basic Concepts 9 1. Topology and holes 5. Some of applications 2. Simplicial complexes 4. Persistent homology 3. Definition of holes
- 10. Simplicial complexes 10 Simplicial complex: A set of vertexes, edges, triangles, tetrahedrons, … that are closed under taking faces and that have no improper intersections vertex (0-dimension) edge (1-dimension) triangle (2-dimension) tetrahedron (3-dimension) simplicial complex not simplicial complex 2 - Simplicial complexes k-simplex
- 11. Simplicial 11 n-simplex: The “smallest” convex hull of n+1 affinity independent points vertex (0-dimension) edge (1-dimension) triangle (2-dimension) tetrahedron (3-dimension) n-simplex = |v0v1...vn| = { 0v0 + 1v1 + ... + nvn| 0 + ... + n = 1, i 0} A m-face of σ is the convex hull τ = |vi0…vim| of a non-empty subset of {v0, v1, …, vn} (and it is proper if the subset is not the entire set) ⌧ 2 - Simplicial complexes
- 12. Simplicial 12 Direction of simplicial: The same direction with permutation <i0i1…in> 1-simplex 2-simplex 3-simplex 2 - Simplicial complexes
- 13. Simplicial complex 13 Definition: A simplicial complex is a finite collection of simplifies K such that (1) If 2 K and for all face ⌧ then ⌧ 2 K (2) If , ⌧ 2 K and ⌧ 6= ? then ⌧ and ⌧ ⌧ The maximum dimension of simplex in K is the dimension of K K2 = {|v0v1v2|, |v0v1|, |v0v2|, |v1v2|, |v0|, |v1|, |v2|} K = K2 [ {|v3v4|, |v3|, |v4|} NOT YES 2 - Simplicial complexes
- 14. Simplicial complexes 14 Hemoglobin simplicial complex Image source: http://www2.math.kyushu-u.ac.jp/~hiraoka/protein_homology.pdf 2 - Simplicial complexes
- 15. ✤ Let be a covering of Nerve 15 = {Bi|i = 1, ..., m} X = [m i=1Bi ✤ The nerve of is a simplicial complex N( ) = (V, ⌃) 2 - Simplicial complexes
- 16. Nerve theorem 16 ✤ If is covered by a collection of convex closed sets then X and are homotopy equivalent X ⊂ RN = {Bi|i = 1, ..., m} N( ) 2 - Simplicial complexes
- 17. Cech complex 17 P = {xi 2 RN |i = 1, ..., m} Br(xi) = {x 2 RN | ||x xi|| r} ✤ The Cech complex C(P, r) is the nerve of ✤ = {Br(xi)| xi 2 P} ✤ From nerve theorem: C(P, r) Xr = [m i=1Br(xi) ' C(P, r) ✤ Filtration ball with radius r 2 - Simplicial complexes
- 18. Cech complex 18 ✤ The weighted Cech complex C(P, R) is the nerve of ✤ Computations to check the intersections of balls are not easy ball with different radius= {Bri (xi)| xi 2 P} Alpha complex 2 - Simplicial complexes
- 19. Voronoi diagrams and Delaunay complex 19 ✤ P = {xi 2 RN |i = 1, ..., m} Vi = {x 2 RN | ||x xi|| ||x xj||, j 6= i} RN = [m i=1Vi Voronoi cell ✤ = {Vi|i = 1, ..., m} D(P) = N( ) Voronoi decomposition Delaunay complex 2 - Simplicial complexes
- 20. General position 20 ✤ is in a general position, if there is no ✤ If all combination of N+2 points in P is in a general position, then P is in a general position x1, ..., xN+2 2 RN x 2 RN s.t.||x x1|| = ... = ||x xN+2|| ✤ If P is in a general position then The dimensions of Delaunay simplexes <= N Geometric representation of D(P) can be embedded in RN 2 - Simplicial complexes
- 21. Alpha complex 21 ✤ ✤ ✤ The alpha complex is the nerve of ↵(P, r) = N( ) ✤ From Nerve theorem: Xr ' ↵(P, r) 2 - Simplicial complexes
- 22. Alpha complex 22 ✤ ✤ ✤ The weighted alpha complex is defined with different radius if P is in a general position filtration of alpha complexes 2 - Simplicial complexes
- 23. Alpha complex 23 ✤ Computations are much easier than Cech complexes ✤ Software: CGAL • Construct alpha complexes of points clouds data in RN with N <= 3 Filtration of alpha complex Image source: http://www2.math.kyushu-u.ac.jp/~hiraoka/protein_homology.pdf 2 - Simplicial complexes
- 24. Outline TDA - Basic Concepts 24 1. Topology and holes 3. Definition of holes 5. Some of applications 2. Simplicial complexes 4. Persistent homology
- 25. Definition of holes 25 Simplicial complex Chain complex Homology group Algebraic Holes Geometrical object Algebraic object 3 - Definition of Holes
- 26. What is hole? 26 ✤ 1-dimensional hole: ring not ring have ring boundary without ring without boundary Ring = 1-dimensional graph without boundary? However, NOT 1-dimensional graph without boundary but is 2-dimensional graph ’s boundary Ring = 1-dimensional graph without boundary and is not boundary of 2-dimensional graph 3 - Definition of Holes
- 27. What is hole? 27 ✤ 2-dimensional hole: cavity not cavity have cavity boundary without cavity without boundary However, NOT 2-dimensional graph without boundary but is 3-dimensional graph ’s boundary Cavity = 2-dimensional graph without boundary and is not boundary of 3-dimensional graph Cavity = 2-dimensional graph without boundary? 3 - Definition of Holes
- 28. Hole and boundary 28 q-dimensional hole q-dimensional graph without boundary and is not boundary of (q+1)-dimensional graph= We try to make it clear by “Algebraic” language 3 - Definition of Holes
- 29. Chain complexes 29 Let K be a simplicial complex with dimension n. The group of q- chains is defined as below: The element of Cq(K) is called q chain. Definition: Cq(K) := { X ↵i ⌦ vi0 ...viq ↵ |↵i 2 R, ⌦ vi0 ...viq ↵ : q simplicial in K} 0 q nif Cq(K) := 0, if q < 0 or q > n 3 - Definition of Holes
- 30. Boundary 30 Boundary of a q-simplex is the sum of its (q-1)-dimensional faces. Definition: vil is omitted @|v0v1v2| := |v0v1| + |v1v2| + |v0v2| 3 - Definition of Holes
- 31. Boundary 31 Fundamental lemma @q 1 @q = 0 @2 @1 For q = 2 In general • For a q - simplex τ, the boundary ∂qτ, consists of all (q-1) faces of τ. • Every (q-2)-face of τ belongs to exactly two (q-1)-faces, with different direction @q 1@q⌧ = 0 3 - Definition of Holes
- 32. Hole and boundary 32 q-dimensional hole q-dimensional graph without boundary and is not boundary of (q+1)-dimensional graph (1) (2) (1) (2) := ker @q := im@q+1 (cycles group) (boundary group) Bq(K) ⇢ Zq(K) ⇢ Cq(K) @q @q+1 = 0 3 - Definition of Holes
- 33. Hole and boundary 33 q-dimensional hole q-dimensional graph without boundary and is not boundary of (q+1)-dimensional graph (1) (2) Elements in Zq(K) remain after make Bq(K) become zero This operator is defined as Q = := ker @q := im@q+1 Q(z0 ) = Q(z) + Q(b) = Q(z) (z and z’ are equivalent in with respect to ) q-dimensional hole = an equivalence class of vectors ker @q im @q+1 For z0 = z + b, z, z0 2 ker @q, b 2 im @q+1 3 - Definition of Holes
- 34. Homology group 34 Homology groups The qth Homology Group Hq is defined as Hq = Ker@q/Im@q+1 = {z + Im@q+1 | z 2 Ker@q } = {[z]|z 2 Ker@q} Divided in groups with operator [z] + [z’] = [z + z’] Betti Numbers The qth Betti Number is defined as the dimension of Hq bq = dim(Hq) H0(K): connected component H1(K): ring H2(K): cavity 3 - Definition of Holes
- 35. Computing Homology 35 v0 v1 v2 v3 All vectors in the column space of Ker@0 are equivalent with respect to Im@1 b0 = dim(H0) = 1 Im@2 has only the zero vector b1 = dim(H1) = 1 H1 = { (|v0v1| + |v1v2| + |v2v3| + |v3v0|)} 3 - Definition of Holes
- 36. Computing Homology 36 v0 v1 v2 v3 H1 = { (hv0v1i + hv1v2i + hv2v3i hv0v3i)} All vectors in the column space of Ker@0 are equivalent with respect to Im@1 b0 = dim(H0) = 1 Im@2 has only the zero vector b1 = dim(H1) = 1 3 - Definition of Holes
- 37. Outline TDA - Basic Concepts 37 1. Topology and holes 3. Definition of holes 5. Some of applications 2. Simplicial complexes 4. Persistent homology
- 38. Persistent Homology Persistent homology 38 ✤ Consider filtration of finite type K : K0 ⇢ K1 ⇢ ... ⇢ Kt ⇢ ... 9 ⇥ s.t. Kj = K⇥ , 8j ⇥ ✤ : total simplicial complexK = [t 0Kt Kk Kt k T( ) = t 2 Kt Kt 1 : all k-simplexes in K : all k-simplexes in K at time t : birth time of the simplex time Slide source: http://www2.math.kyushu-u.ac.jp/~hiraoka/protein_homology.pdf
- 39. Persistent Homology 39 ✤ Z2 - vector space ✤ Z2[x] - graded module ✤ Inclusion map ✤ is a free Z2[x] module with the baseCk(K) Persistent homology Slide source: http://www2.math.kyushu-u.ac.jp/~hiraoka/protein_homology.pdf
- 40. Persistent Homology 40 ✤ Boundary map ✤ From the graded structure ✤ Persistent homology (graded homomorphism) face of σ Persistent homology Slide source: http://www2.math.kyushu-u.ac.jp/~hiraoka/protein_homology.pdf
- 41. Persistent Homology 41 ✤ From the structure theorem of Z2[x] (PID) ✤ Persistent interval ✤ Persistent diagram Ii(b): inf of Ii, Ii(d): sup of Ii Persistent homology Slide source: http://www2.math.kyushu-u.ac.jp/~hiraoka/protein_homology.pdf
- 42. Persistent Homology 42 birth time death time ✤ “Hole” appears close to the diagonal may be the “noise” ✤ “Hole” appears far to the diagonal may be the “noise” ✤ Detect the “structure hole” Persistent homology Slide source: http://www2.math.kyushu-u.ac.jp/~hiraoka/protein_homology.pdf
- 43. Outline TDA - Basic Concepts 43 1. Topology and holes 3. Definition of holes 5. Some of applications 2. Simplicial complexes 4. Persistent homology see more at part2 of tutorial
- 44. Applications 5 - Some of applications 44 • Persistence to Protein compressibility Marcio Gameiro et. al. (Japan J. Indust. Appl. Math (2015) 32:1-17)
- 45. Protein Structure Persistence to protein compressibility 45 amino acid 1 amino acid 2 3-dim structure of hemoglobin 1-dim structure of protein folding peptide bond Slide source: http://www2.math.kyushu-u.ac.jp/~hiraoka/protein_homology.pdf
- 46. Protein Structure Persistence to protein compressibility 46 ✤ Van der Waals radius of an atom H: 1.2, C: 1.7, N: 1.55 (A0) O: 1.52, S: 1.8, P: 1.8 (A0) Slide source: http://www2.math.kyushu-u.ac.jp/~hiraoka/protein_homology.pdf Van der Waals ball model of hemoglobin
- 47. Alpha Complex for Protein Modeling Persistence to protein compressibility 47 ✤ ✤ ✤ : position of atoms : radius of i-th atom : weighted Voronoi Decomposition : power distance : ball with radius ri Slide source: http://www2.math.kyushu-u.ac.jp/~hiraoka/protein_homology.pdf
- 48. Alpha Complex for Protein Modeling Persistence to protein compressibility 48 ✤ ✤ ✤ Alpha complex nerve k - simplex Nerve lemma Changing radius to form a filtration (by w) Slide source: http://www2.math.kyushu-u.ac.jp/~hiraoka/protein_homology.pdf
- 49. Topology of Ovalbumin Persistence to protein compressibility 49 birth time deathtime birth time deathtime 1st betti plot 2nd betti plot PD1 PD2 Slide source: http://www2.math.kyushu-u.ac.jp/~hiraoka/protein_homology.pdf
- 50. Compressibility Persistence to protein compressibility 50 3-dim structureFunctionality Softness Compressibility Experiments Quantification Persistence diagrams (Difficult) …..….. Select generators and fitting parameters with experimental compressibility holes
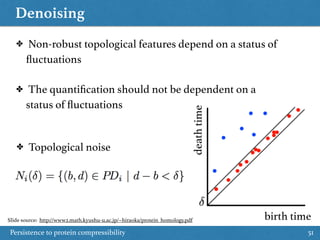
- 51. Denoising Persistence to protein compressibility 51 birth time deathtime ✤ Topological noise ✤ Non-robust topological features depend on a status of fluctuations ✤ The quantification should not be dependent on a status of fluctuations Slide source: http://www2.math.kyushu-u.ac.jp/~hiraoka/protein_homology.pdf
- 52. Holes with Sparse or Dense Boundary Persistence to protein compressibility 52 ✤ A sparse hole structure is deformable to a much larger extent than the dense hole → greater compressibility ✤ Effective sparse holes : van der Waals ball : enlarged ball birth time deathtime Slide source: http://www2.math.kyushu-u.ac.jp/~hiraoka/protein_homology.pdf
- 53. # of generators v.s. compressibility Persistence to protein compressibility 53 # of generators v.s. compressibility Topological Measurement Cp Compressibility Slide source: http://www2.math.kyushu-u.ac.jp/~hiraoka/protein_homology.pdf
- 54. Applications 5 - Some of applications 54 • Persistence to Phylogenetic Trees
- 55. Protein Phylogenetic Tree Persistence to Phylogenetic Trees 55 ✤ Phylogenetic tree is defined by a distance matrix for a set of species (human, dog, frog, fish,…) ✤ The distance matrix is calculated by a score function based on similarity of amino acid sequences amino acid sequences fish hemoglobin frog hemoglobin human hemoglobin distance matrix of hemoglobin fish frog human dog Slide source: http://www2.math.kyushu-u.ac.jp/~hiraoka/protein_homology.pdf
- 56. Persistence Distance and Classification of Proteins Persistence to Phylogenetic Trees 56 ✤ The score function based on amnio acid sequences does not contain information of 3-dim structure of proteins ✤ Wasserstein distance (of degree p) Cohen-Steiner, Edelsbrunner, Harer, and Mileyko, FCM, 2010 on persistence diagrams reflects similarity of persistence diagram (3-dim structures) of proteins Slide source: http://www2.math.kyushu-u.ac.jp/~hiraoka/protein_homology.pdf
- 57. Persistence Distance and Classification of Proteins Persistence to Phylogenetic Trees 57 birth time deathtime birth time birth time deathtime deathtimeWasserstein distance Bijection Slide source: http://www2.math.kyushu-u.ac.jp/~hiraoka/protein_homology.pdf
- 58. Distance between persistence diagrams Persistence to Phylogenetic Trees 58 Persistence of sub level sets Stability Theorem (Cohen-Steiner et al., 2010) birth time deathtime Slide source: http://www2.math.kyushu-u.ac.jp/~hiraoka/protein_homology.pdf
- 59. Phylogenetic Tree by Persistence Persistence to Phylogenetic Trees 59 ✤ Apply the distance on persistence diagrams to classify proteins Persistence diagram used the noise band same as in the computations of compressibility 3DHT 3D1A 1QPW 3LQD 1FAW 1C40 2FZB Slide source: http://www2.math.kyushu-u.ac.jp/~hiraoka/protein_homology.pdf
- 60. Future work TDA - Basic Concepts 60 ✤ Principle to de-noise fluctuations in persistence diagrams (NMR experiments) ✤ Finding minimum generators to identify specific regions in a protein (e.g., a region inducing high compressibility, hereditarily important regions) ✤ Zigzag persistence for robust topological features among a specific group of proteins (quiver representation) ✤ Multi-dimensional persistence (PID → Grobner basic) Slide source: http://www2.math.kyushu-u.ac.jp/~hiraoka/protein_homology.pdf
- 61. Applications more in part … of tutorials 5 - Some of applications 61 ✤ Robotics ✤ Computer Visions ✤ Sensor network ✤ Concurrency & database ✤ Visualization Prof. Robert Ghrist Department of Mathematics University of Pennsylvania One of pioneers in applications Michael Farber Edelsbrunner Mischaikow Gaucher Bubenik Zomorodian Carlsson
- 62. Software TDA - Basic Concepts 62 • Alpha complex by CGAL http://www.cgal.org/ • Persistence diagrams by Perseus (coded by Vidit Nanda) http://www.sas.upenn.edu/~vnanda/perseus/index.html http://chomp.rutgers.edu/Project.html • CHomP project
- 63. Reference links TDA - Basic Concepts 63 • Yasuaki Hiraoka associate professor homepage http://www2.math.kyushu-u.ac.jp/~hiraoka/site/About_Me.html http://www2.math.kyushu-u.ac.jp/~hiraoka/protein_homology.pdf www.msys.sys.i.kyoto-u.ac.jp/~kazunori/paper/nist20081219.pdf • Applications in sensor network