06DynamicProgramming in algorithms CSE.pdf
- 1. Lecture slides by Kevin Wayne Copyright © 2005 Pearson-Addison Wesley http://www.cs.princeton.edu/~wayne/kleinberg-tardos Last updated on 2/10/21 2:39 PM 6. DYNAMIC PROGRAMMING I ‣ weighted interval scheduling ‣ segmented least squares ‣ knapsack problem ‣ RNA secondary structure
- 2. Algorithmic paradigms Greed. Process the input in some order, myopically making irrevocable decisions. Divide-and-conquer. Break up a problem into independent subproblems; solve each subproblem; combine solutions to subproblems to form solution to original problem. Dynamic programming. Break up a problem into a series of overlapping subproblems; combine solutions to smaller subproblems to form solution to large subproblem. 2 fancy name for caching intermediate results in a table for later reuse
- 3. Dynamic programming history Bellman. Pioneered the systematic study of dynamic programming in 1950s. Etymology. ・Dynamic programming = planning over time. ・Secretary of Defense had pathological fear of mathematical research. ・Bellman sought a “dynamic” adjective to avoid conflict. 3 THE THEORY OF DYNAMIC PROGRAMMING RICHARD BELLMAN 1. Introduction. Before turning to a discussion of some representa- tive problems which will permit us to exhibit various mathematical features of the theory, let us present a brief survey of the funda- mental concepts, hopes, and aspirations of dynamic programming. To begin with, the theory was created to treat the mathematical problems arising from the study of various multi-stage decision processes, which may roughly be described in the following way: We have a physical system whose state at any time / is determined by a set of quantities which we call state parameters, or state variables. At certain times, which may be prescribed in advance, or which may be determined by the process itself, we are called upon to make de- cisions which will affect the state of the system. These decisions are equivalent to transformations of the state variables, the choice of a decision being identical with the choice of a transformation. The out- come of the preceding decisions is to be used to guide the choice of future ones, with the purpose of the whole process that of maximizing some function of the parameters describing the final state. Examples of processes fitting this loose description are furnished by virtually every phase of modern life, from the planning of indus- trial production lines to the scheduling of patients at a medical clinic ; from the determination of long-term investment programs for universities to the determination of a replacement policy for ma- chinery in factories; from the programming of training policies for skilled and unskilled labor to the choice of optimal purchasing and in- ventory policies for department stores and military establishments. It is abundantly clear from the very brief description of possible applications that the problems arising from the study of these processes are problems of the future as well as of the immediate present.
- 4. Dynamic programming applications Application areas. ・Computer science: AI, compilers, systems, graphics, theory, …. ・Operations research. ・Information theory. ・Control theory. ・Bioinformatics. Some famous dynamic programming algorithms. ・Avidan–Shamir for seam carving. ・Unix diff for comparing two files. ・Viterbi for hidden Markov models. ・De Boor for evaluating spline curves. ・Bellman–Ford–Moore for shortest path. ・Knuth–Plass for word wrapping text in . ・Cocke–Kasami–Younger for parsing context-free grammars. ・Needleman–Wunsch/Smith–Waterman for sequence alignment. 4 T1X <latexit sha1_base64="EhG7/UUHfhF6o3p74Glw1DH78ik=">AAACK3icbVBNS8NAEN34WetXW49egkXwVBIRrLeCF48VGltoQ9lspu3SzSbsTqQl9C941V/hr/GiePV/mKQ52NYHC4/3ZnZmnhcJrtGyPo2t7Z3dvf3SQfnw6PjktFKtPekwVgwcFopQ9TyqQXAJDnIU0IsU0MAT0PWm95nffQaleSg7OI/ADehY8hFnFDNp0IHesFK3GlYOc5PYBamTAu1h1agN/JDFAUhkgmrdt60I3YQq5EzAojyINUSUTekY+imVNADtJvmyC/MyVXxzFKr0STRz9W9HQgOt54GXVgYUJ3rdy8T/vH6Mo6abcBnFCJItB41iYWJoZpebPlfAUMxTQpni6a4mm1BFGab5rEzJ/46ArVySzGLJWejDmipwhoou0hTt9cw2iXPduGvYjzf1VrOIs0TOyQW5Ija5JS3yQNrEIYxMyAt5JW/Gu/FhfBnfy9Ito+g5Iyswfn4BrkOohg==</latexit> <latexit sha1_base64="EhG7/UUHfhF6o3p74Glw1DH78ik=">AAACK3icbVBNS8NAEN34WetXW49egkXwVBIRrLeCF48VGltoQ9lspu3SzSbsTqQl9C941V/hr/GiePV/mKQ52NYHC4/3ZnZmnhcJrtGyPo2t7Z3dvf3SQfnw6PjktFKtPekwVgwcFopQ9TyqQXAJDnIU0IsU0MAT0PWm95nffQaleSg7OI/ADehY8hFnFDNp0IHesFK3GlYOc5PYBamTAu1h1agN/JDFAUhkgmrdt60I3YQq5EzAojyINUSUTekY+imVNADtJvmyC/MyVXxzFKr0STRz9W9HQgOt54GXVgYUJ3rdy8T/vH6Mo6abcBnFCJItB41iYWJoZpebPlfAUMxTQpni6a4mm1BFGab5rEzJ/46ArVySzGLJWejDmipwhoou0hTt9cw2iXPduGvYjzf1VrOIs0TOyQW5Ija5JS3yQNrEIYxMyAt5JW/Gu/FhfBnfy9Ito+g5Iyswfn4BrkOohg==</latexit> <latexit sha1_base64="EhG7/UUHfhF6o3p74Glw1DH78ik=">AAACK3icbVBNS8NAEN34WetXW49egkXwVBIRrLeCF48VGltoQ9lspu3SzSbsTqQl9C941V/hr/GiePV/mKQ52NYHC4/3ZnZmnhcJrtGyPo2t7Z3dvf3SQfnw6PjktFKtPekwVgwcFopQ9TyqQXAJDnIU0IsU0MAT0PWm95nffQaleSg7OI/ADehY8hFnFDNp0IHesFK3GlYOc5PYBamTAu1h1agN/JDFAUhkgmrdt60I3YQq5EzAojyINUSUTekY+imVNADtJvmyC/MyVXxzFKr0STRz9W9HQgOt54GXVgYUJ3rdy8T/vH6Mo6abcBnFCJItB41iYWJoZpebPlfAUMxTQpni6a4mm1BFGab5rEzJ/46ArVySzGLJWejDmipwhoou0hTt9cw2iXPduGvYjzf1VrOIs0TOyQW5Ija5JS3yQNrEIYxMyAt5JW/Gu/FhfBnfy9Ito+g5Iyswfn4BrkOohg==</latexit> <latexit sha1_base64="K4LIWrwvep29t51jV7N8ecuok+0=">AAACGXicbVBNT8JAEN3iFyIqePWykZh4Iq0X9WbixSMmVkigIdvtFDZst83u1EAa/oBXf4W/xpMx/huXwkHAl2zy8t7MzswLMykMuu6PU9nZ3ds/qB7Wjuq145PTRv3FpLnm4PNUproXMgNSKPBRoIRepoEloYRuOHlY+N1X0Eak6hlnGQQJGykRC87QSp1ho+W23RJ0m3gr0iIrDJvO2SBKeZ6AQi6ZMX3PzTAomEbBJcxrg9xAxviEjaBvqWIJmKAo95zTS6tENE61fQppqf7tKFhizCwJbWXCcGw2vYX4n9fPMb4NCqGyHEHx5aA4lxRTujiaRkIDRzmzhHEt7K6Uj5lmHG00a1PKvzPga5cU01wJnkawoUqcomZzG6K3Gdk28a/bd23vySVVck4uyBXxyA25J4+kQ3zCSUTeyLvz4Xw6X8usK84q9CZZg/P9C1n2pHk=</latexit> <latexit sha1_base64="SWKETCWkcgZ0sm6ZDiXeRUTM5+0=">AAACIHicbVBNT8JAEJ36iYgKXL1sJCaeSOtFvZl48YgJCAk0ZLsMsGG7bXanBtLwF7zqr/DXeNH4YyyFg4Av2eTlvZmdmRfESlpy3S9nZ3dv/+CwcFQ8Lp2cnpUrpWcbJUZgS0QqMp2AW1RSY4skKezEBnkYKGwHk4eF335BY2WkmzSL0Q/5SMuhFJwWUq+JnX655tbdHGybeCtSgxUa/YpT7Q0ikYSoSShubddzY/JTbkgKhfNiL7EYczHhI+xmVPMQrZ/my87ZZaYM2DAy2dPEcvVvR8pDa2dhkFWGnMZ201uI/3ndhIa3fip1nBBqsRw0TBSjiC0uZwNpUJCaZYQLI7NdmRhzwwVl+axNyf+OUaxdkk4TLUU0wA1V0ZQMn2cpepuZbZPWdf2u7j25UIBzuIAr8OAG7uERGtACAWN4hTd4dz6cT+d7GfeOs8q9Cmtwfn4BcFCm+g==</latexit> <latexit sha1_base64="SWKETCWkcgZ0sm6ZDiXeRUTM5+0=">AAACIHicbVBNT8JAEJ36iYgKXL1sJCaeSOtFvZl48YgJCAk0ZLsMsGG7bXanBtLwF7zqr/DXeNH4YyyFg4Av2eTlvZmdmRfESlpy3S9nZ3dv/+CwcFQ8Lp2cnpUrpWcbJUZgS0QqMp2AW1RSY4skKezEBnkYKGwHk4eF335BY2WkmzSL0Q/5SMuhFJwWUq+JnX655tbdHGybeCtSgxUa/YpT7Q0ikYSoSShubddzY/JTbkgKhfNiL7EYczHhI+xmVPMQrZ/my87ZZaYM2DAy2dPEcvVvR8pDa2dhkFWGnMZ201uI/3ndhIa3fip1nBBqsRw0TBSjiC0uZwNpUJCaZYQLI7NdmRhzwwVl+axNyf+OUaxdkk4TLUU0wA1V0ZQMn2cpepuZbZPWdf2u7j25UIBzuIAr8OAG7uERGtACAWN4hTd4dz6cT+d7GfeOs8q9Cmtwfn4BcFCm+g==</latexit> <latexit sha1_base64="HJV6YlmlVjnPgPYqeSt99ZGHmBg=">AAACK3icbVBNT8JAEN3iF+IX4NFLIzHxRFov4o3Ei0dMqJBAQ7bbATZst83u1EAa/oJX/RX+Gi8ar/4P29KDgC/Z5OW9mZ2Z50WCa7SsT6O0s7u3f1A+rBwdn5yeVWv1Jx3GioHDQhGqvkc1CC7BQY4C+pECGngCet7sPvN7z6A0D2UXFxG4AZ1IPuaMYiYNu9AfVRtW08phbhO7IA1SoDOqGfWhH7I4AIlMUK0HthWhm1CFnAlYVoaxhoiyGZ3AIKWSBqDdJF92aV6lim+OQ5U+iWau/u1IaKD1IvDSyoDiVG96mfifN4hx3HITLqMYQbLVoHEsTAzN7HLT5woYikVKKFM83dVkU6oowzSftSn53xGwtUuSeSw5C33YUAXOUdFlmqK9mdk2cW6ad0370Wq0W0WcZXJBLsk1scktaZMH0iEOYWRKXsgreTPejQ/jy/helZaMouecrMH4+QWtA6iC</latexit> <latexit sha1_base64="EhG7/UUHfhF6o3p74Glw1DH78ik=">AAACK3icbVBNS8NAEN34WetXW49egkXwVBIRrLeCF48VGltoQ9lspu3SzSbsTqQl9C941V/hr/GiePV/mKQ52NYHC4/3ZnZmnhcJrtGyPo2t7Z3dvf3SQfnw6PjktFKtPekwVgwcFopQ9TyqQXAJDnIU0IsU0MAT0PWm95nffQaleSg7OI/ADehY8hFnFDNp0IHesFK3GlYOc5PYBamTAu1h1agN/JDFAUhkgmrdt60I3YQq5EzAojyINUSUTekY+imVNADtJvmyC/MyVXxzFKr0STRz9W9HQgOt54GXVgYUJ3rdy8T/vH6Mo6abcBnFCJItB41iYWJoZpebPlfAUMxTQpni6a4mm1BFGab5rEzJ/46ArVySzGLJWejDmipwhoou0hTt9cw2iXPduGvYjzf1VrOIs0TOyQW5Ija5JS3yQNrEIYxMyAt5JW/Gu/FhfBnfy9Ito+g5Iyswfn4BrkOohg==</latexit> <latexit sha1_base64="EhG7/UUHfhF6o3p74Glw1DH78ik=">AAACK3icbVBNS8NAEN34WetXW49egkXwVBIRrLeCF48VGltoQ9lspu3SzSbsTqQl9C941V/hr/GiePV/mKQ52NYHC4/3ZnZmnhcJrtGyPo2t7Z3dvf3SQfnw6PjktFKtPekwVgwcFopQ9TyqQXAJDnIU0IsU0MAT0PWm95nffQaleSg7OI/ADehY8hFnFDNp0IHesFK3GlYOc5PYBamTAu1h1agN/JDFAUhkgmrdt60I3YQq5EzAojyINUSUTekY+imVNADtJvmyC/MyVXxzFKr0STRz9W9HQgOt54GXVgYUJ3rdy8T/vH6Mo6abcBnFCJItB41iYWJoZpebPlfAUMxTQpni6a4mm1BFGab5rEzJ/46ArVySzGLJWejDmipwhoou0hTt9cw2iXPduGvYjzf1VrOIs0TOyQW5Ija5JS3yQNrEIYxMyAt5JW/Gu/FhfBnfy9Ito+g5Iyswfn4BrkOohg==</latexit> <latexit sha1_base64="EhG7/UUHfhF6o3p74Glw1DH78ik=">AAACK3icbVBNS8NAEN34WetXW49egkXwVBIRrLeCF48VGltoQ9lspu3SzSbsTqQl9C941V/hr/GiePV/mKQ52NYHC4/3ZnZmnhcJrtGyPo2t7Z3dvf3SQfnw6PjktFKtPekwVgwcFopQ9TyqQXAJDnIU0IsU0MAT0PWm95nffQaleSg7OI/ADehY8hFnFDNp0IHesFK3GlYOc5PYBamTAu1h1agN/JDFAUhkgmrdt60I3YQq5EzAojyINUSUTekY+imVNADtJvmyC/MyVXxzFKr0STRz9W9HQgOt54GXVgYUJ3rdy8T/vH6Mo6abcBnFCJItB41iYWJoZpebPlfAUMxTQpni6a4mm1BFGab5rEzJ/46ArVySzGLJWejDmipwhoou0hTt9cw2iXPduGvYjzf1VrOIs0TOyQW5Ija5JS3yQNrEIYxMyAt5JW/Gu/FhfBnfy9Ito+g5Iyswfn4BrkOohg==</latexit> <latexit sha1_base64="EhG7/UUHfhF6o3p74Glw1DH78ik=">AAACK3icbVBNS8NAEN34WetXW49egkXwVBIRrLeCF48VGltoQ9lspu3SzSbsTqQl9C941V/hr/GiePV/mKQ52NYHC4/3ZnZmnhcJrtGyPo2t7Z3dvf3SQfnw6PjktFKtPekwVgwcFopQ9TyqQXAJDnIU0IsU0MAT0PWm95nffQaleSg7OI/ADehY8hFnFDNp0IHesFK3GlYOc5PYBamTAu1h1agN/JDFAUhkgmrdt60I3YQq5EzAojyINUSUTekY+imVNADtJvmyC/MyVXxzFKr0STRz9W9HQgOt54GXVgYUJ3rdy8T/vH6Mo6abcBnFCJItB41iYWJoZpebPlfAUMxTQpni6a4mm1BFGab5rEzJ/46ArVySzGLJWejDmipwhoou0hTt9cw2iXPduGvYjzf1VrOIs0TOyQW5Ija5JS3yQNrEIYxMyAt5JW/Gu/FhfBnfy9Ito+g5Iyswfn4BrkOohg==</latexit> <latexit sha1_base64="EhG7/UUHfhF6o3p74Glw1DH78ik=">AAACK3icbVBNS8NAEN34WetXW49egkXwVBIRrLeCF48VGltoQ9lspu3SzSbsTqQl9C941V/hr/GiePV/mKQ52NYHC4/3ZnZmnhcJrtGyPo2t7Z3dvf3SQfnw6PjktFKtPekwVgwcFopQ9TyqQXAJDnIU0IsU0MAT0PWm95nffQaleSg7OI/ADehY8hFnFDNp0IHesFK3GlYOc5PYBamTAu1h1agN/JDFAUhkgmrdt60I3YQq5EzAojyINUSUTekY+imVNADtJvmyC/MyVXxzFKr0STRz9W9HQgOt54GXVgYUJ3rdy8T/vH6Mo6abcBnFCJItB41iYWJoZpebPlfAUMxTQpni6a4mm1BFGab5rEzJ/46ArVySzGLJWejDmipwhoou0hTt9cw2iXPduGvYjzf1VrOIs0TOyQW5Ija5JS3yQNrEIYxMyAt5JW/Gu/FhfBnfy9Ito+g5Iyswfn4BrkOohg==</latexit> <latexit sha1_base64="EhG7/UUHfhF6o3p74Glw1DH78ik=">AAACK3icbVBNS8NAEN34WetXW49egkXwVBIRrLeCF48VGltoQ9lspu3SzSbsTqQl9C941V/hr/GiePV/mKQ52NYHC4/3ZnZmnhcJrtGyPo2t7Z3dvf3SQfnw6PjktFKtPekwVgwcFopQ9TyqQXAJDnIU0IsU0MAT0PWm95nffQaleSg7OI/ADehY8hFnFDNp0IHesFK3GlYOc5PYBamTAu1h1agN/JDFAUhkgmrdt60I3YQq5EzAojyINUSUTekY+imVNADtJvmyC/MyVXxzFKr0STRz9W9HQgOt54GXVgYUJ3rdy8T/vH6Mo6abcBnFCJItB41iYWJoZpebPlfAUMxTQpni6a4mm1BFGab5rEzJ/46ArVySzGLJWejDmipwhoou0hTt9cw2iXPduGvYjzf1VrOIs0TOyQW5Ija5JS3yQNrEIYxMyAt5JW/Gu/FhfBnfy9Ito+g5Iyswfn4BrkOohg==</latexit>
- 6. 6. DYNAMIC PROGRAMMING I ‣ weighted interval scheduling ‣ segmented least squares ‣ knapsack problem ‣ RNA secondary structure SECTIONS 6.1–6.2
- 7. Weighted interval scheduling ・Job j starts at sj, finishes at fj, and has weight wj > 0. ・Two jobs are compatible if they don’t overlap. ・Goal: find max-weight subset of mutually compatible jobs. 7 time f g h e a b c d 0 1 2 3 4 5 6 7 8 9 10 11 sj fj wj
- 8. Earliest-finish-time first algorithm Earliest finish-time first. ・Consider jobs in ascending order of finish time. ・Add job to subset if it is compatible with previously chosen jobs. Recall. Greedy algorithm is correct if all weights are 1. Observation. Greedy algorithm fails spectacularly for weighted version. 8 weight = 999 weight = 1 time 0 1 2 3 4 5 6 7 8 9 10 11 b a h weight = 1
- 9. Weighted interval scheduling Convention. Jobs are in ascending order of finish time: f1 ≤ f2 ≤ . . . ≤ fn . Def. p(j) = largest index i < j such that job i is compatible with j. Ex. p(8) = 1, p(7) = 3, p(2) = 0. 9 time 0 1 2 3 4 5 6 7 8 9 10 11 6 7 8 4 3 1 2 5 i is rightmost interval that ends before j begins
- 10. Dynamic programming: binary choice Def. OPT(j) = max weight of any subset of mutually compatible jobs for subproblem consisting only of jobs 1, 2, ..., j. Goal. OPT(n) = max weight of any subset of mutually compatible jobs. Case 1. OPT(j) does not select job j. ・Must be an optimal solution to problem consisting of remaining jobs 1, 2, ..., j – 1. Case 2. OPT(j) selects job j. ・Collect profit wj. ・Can’t use incompatible jobs { p(j) + 1, p(j) + 2, ..., j – 1 }. ・Must include optimal solution to problem consisting of remaining compatible jobs 1, 2, ..., p(j). Bellman equation. 10 optimal substructure property (proof via exchange argument) OPT(j) = 0 B7 j = 0 max { OPT(j 1), wj + OPT(p(j)) } B7 j > 0 <latexit sha1_base64="qEOy02oDztIDL8rE3HZJCxx6JUo=">AAACxnicbVHbattAEF0pvaTuzUkf+zLUtMQ0NVJSaIpJCfSlfaoLcRPwCrNajex1Viuxu2pshKE/0g/r33Sl6KG2O7BwODN7ZuZMXEhhbBD88fy9e/cfPNx/1Hn85Omz592Dwx8mLzXHMc9lrq9jZlAKhWMrrMTrQiPLYolX8c3nOn/1E7URubq0qwKjjM2USAVn1lHT7u9vo8ujRR/o8JwOOzTGmVAVd4Jm3aHDAN4Atbi0UIFIYQ0LOIcAKJ0MTjGLXAXN2BKoxNQCrYAeQ6P3LuwfO0m4nS7gbUMVrkm/zlMtZnNXvN6V/tRIdyiqpB1h2u0Fg6AJ2AVhC3qkjdH0wDukSc7LDJXlkhkzCYPCRhXTVnCJbqfSYMH4DZvhxEHFMjRR1fi4hteOSSDNtXvKQsP++6NimTGrLHaVGbNzs52ryf/lJqVNz6JKqKK0qPhdo7SUYHOojwKJ0MitXDnAuBZuVuBzphm37nQbXRrtAvnGJtWyVILnCW6x0i6tZrWL4bZnu2B8Mvg4CL+/712ctXbuk5fkFTkiIflALsgXMiJjwr09r++deKf+Vz/3S//2rtT32j8vyEb4v/4CZY/TYA==</latexit> <latexit sha1_base64="qEOy02oDztIDL8rE3HZJCxx6JUo=">AAACxnicbVHbattAEF0pvaTuzUkf+zLUtMQ0NVJSaIpJCfSlfaoLcRPwCrNajex1Viuxu2pshKE/0g/r33Sl6KG2O7BwODN7ZuZMXEhhbBD88fy9e/cfPNx/1Hn85Omz592Dwx8mLzXHMc9lrq9jZlAKhWMrrMTrQiPLYolX8c3nOn/1E7URubq0qwKjjM2USAVn1lHT7u9vo8ujRR/o8JwOOzTGmVAVd4Jm3aHDAN4Atbi0UIFIYQ0LOIcAKJ0MTjGLXAXN2BKoxNQCrYAeQ6P3LuwfO0m4nS7gbUMVrkm/zlMtZnNXvN6V/tRIdyiqpB1h2u0Fg6AJ2AVhC3qkjdH0wDukSc7LDJXlkhkzCYPCRhXTVnCJbqfSYMH4DZvhxEHFMjRR1fi4hteOSSDNtXvKQsP++6NimTGrLHaVGbNzs52ryf/lJqVNz6JKqKK0qPhdo7SUYHOojwKJ0MitXDnAuBZuVuBzphm37nQbXRrtAvnGJtWyVILnCW6x0i6tZrWL4bZnu2B8Mvg4CL+/712ctXbuk5fkFTkiIflALsgXMiJjwr09r++deKf+Vz/3S//2rtT32j8vyEb4v/4CZY/TYA==</latexit> <latexit sha1_base64="qEOy02oDztIDL8rE3HZJCxx6JUo=">AAACxnicbVHbattAEF0pvaTuzUkf+zLUtMQ0NVJSaIpJCfSlfaoLcRPwCrNajex1Viuxu2pshKE/0g/r33Sl6KG2O7BwODN7ZuZMXEhhbBD88fy9e/cfPNx/1Hn85Omz592Dwx8mLzXHMc9lrq9jZlAKhWMrrMTrQiPLYolX8c3nOn/1E7URubq0qwKjjM2USAVn1lHT7u9vo8ujRR/o8JwOOzTGmVAVd4Jm3aHDAN4Atbi0UIFIYQ0LOIcAKJ0MTjGLXAXN2BKoxNQCrYAeQ6P3LuwfO0m4nS7gbUMVrkm/zlMtZnNXvN6V/tRIdyiqpB1h2u0Fg6AJ2AVhC3qkjdH0wDukSc7LDJXlkhkzCYPCRhXTVnCJbqfSYMH4DZvhxEHFMjRR1fi4hteOSSDNtXvKQsP++6NimTGrLHaVGbNzs52ryf/lJqVNz6JKqKK0qPhdo7SUYHOojwKJ0MitXDnAuBZuVuBzphm37nQbXRrtAvnGJtWyVILnCW6x0i6tZrWL4bZnu2B8Mvg4CL+/712ctXbuk5fkFTkiIflALsgXMiJjwr09r++deKf+Vz/3S//2rtT32j8vyEb4v/4CZY/TYA==</latexit> <latexit sha1_base64="qEOy02oDztIDL8rE3HZJCxx6JUo=">AAACxnicbVHbattAEF0pvaTuzUkf+zLUtMQ0NVJSaIpJCfSlfaoLcRPwCrNajex1Viuxu2pshKE/0g/r33Sl6KG2O7BwODN7ZuZMXEhhbBD88fy9e/cfPNx/1Hn85Omz592Dwx8mLzXHMc9lrq9jZlAKhWMrrMTrQiPLYolX8c3nOn/1E7URubq0qwKjjM2USAVn1lHT7u9vo8ujRR/o8JwOOzTGmVAVd4Jm3aHDAN4Atbi0UIFIYQ0LOIcAKJ0MTjGLXAXN2BKoxNQCrYAeQ6P3LuwfO0m4nS7gbUMVrkm/zlMtZnNXvN6V/tRIdyiqpB1h2u0Fg6AJ2AVhC3qkjdH0wDukSc7LDJXlkhkzCYPCRhXTVnCJbqfSYMH4DZvhxEHFMjRR1fi4hteOSSDNtXvKQsP++6NimTGrLHaVGbNzs52ryf/lJqVNz6JKqKK0qPhdo7SUYHOojwKJ0MitXDnAuBZuVuBzphm37nQbXRrtAvnGJtWyVILnCW6x0i6tZrWL4bZnu2B8Mvg4CL+/712ctXbuk5fkFTkiIflALsgXMiJjwr09r++deKf+Vz/3S//2rtT32j8vyEb4v/4CZY/TYA==</latexit>
- 11. Weighted interval scheduling: brute force 11 BRUTE-FORCE (n, s1, …, sn, f1, …, fn, w1, …, wn) _________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Sort jobs by finish time and renumber so that f1 ≤ f2 ≤ … ≤ fn. Compute p[1], p[2], …, p[n] via binary search. RETURN COMPUTE-OPT(n). COMPUTE-OPT( j ) _________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ IF (j = 0) RETURN 0. ELSE RETURN max {COMPUTE-OPT( j – 1), wj + COMPUTE-OPT(p[ j ]) }.
- 12. What is running time of COMPUTE-OPT(n) in the worst case? A. Θ(n log n) B. Θ(n2 ) C. Θ(1.618n ) D. Θ(2n ) 12 Dynamic programming: quiz 1 COMPUTE-OPT( j ) _________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ IF (j = 0) RETURN 0. ELSE RETURN max {COMPUTE-OPT( j – 1), wj + COMPUTE-OPT(p[ j ]) }. T(n) = (1) B7 n = 1 2T(n 1) + (1) B7 n > 1 <latexit sha1_base64="eY4cuuNdtPSoc87X0TvZnXEtJMc=">AAACsXicdVFtaxNBEN4732p8S6vfRBlMlZRiuCuFVopS8IsfKyS2mDvi3t5csmRv79idk4Qj3/2L/gl/g3vpCSbVgV0enpl5ZvbZpFTSUhD89Pxbt+/cvbdzv/Pg4aPHT7q7e19sURmBI1Gowlwl3KKSGkckSeFVaZDnicLLZP6xyV9+R2NloYe0LDHO+VTLTApOjpp0fwz7+gCiM3jfXJ0owanUtXCKdtWJzqLhDIn3wwN4AxHhgmqQGexrVx7uwwqiaDw4wTx2pUdOCd5C2KgdOi34b++HP72dCHXaDpt0e8EgWAfcBGELeqyNi8mutxelhahy1CQUt3YcBiXFNTckhUK3fWWx5GLOpzh2UPMcbVyvLVvBa8ekkBXGHU2wZv/uqHlu7TJPXGXOaWa3cw35r9y4ouw0rqUuK0ItrgdllQIqoPEfUmlQkFo6wIWRblcQM264IPdLG1PW2iWKjZfUi0pLUaS4xSpakOGNi+G2ZzfB6GjwbhB+Pu6dn7Z27rDn7BXrs5CdsHP2iV2wERPsl/fMe+G99I/9r/43P7ku9b225ynbCH/+G90py9g=</latexit> <latexit sha1_base64="eY4cuuNdtPSoc87X0TvZnXEtJMc=">AAACsXicdVFtaxNBEN4732p8S6vfRBlMlZRiuCuFVopS8IsfKyS2mDvi3t5csmRv79idk4Qj3/2L/gl/g3vpCSbVgV0enpl5ZvbZpFTSUhD89Pxbt+/cvbdzv/Pg4aPHT7q7e19sURmBI1Gowlwl3KKSGkckSeFVaZDnicLLZP6xyV9+R2NloYe0LDHO+VTLTApOjpp0fwz7+gCiM3jfXJ0owanUtXCKdtWJzqLhDIn3wwN4AxHhgmqQGexrVx7uwwqiaDw4wTx2pUdOCd5C2KgdOi34b++HP72dCHXaDpt0e8EgWAfcBGELeqyNi8mutxelhahy1CQUt3YcBiXFNTckhUK3fWWx5GLOpzh2UPMcbVyvLVvBa8ekkBXGHU2wZv/uqHlu7TJPXGXOaWa3cw35r9y4ouw0rqUuK0ItrgdllQIqoPEfUmlQkFo6wIWRblcQM264IPdLG1PW2iWKjZfUi0pLUaS4xSpakOGNi+G2ZzfB6GjwbhB+Pu6dn7Z27rDn7BXrs5CdsHP2iV2wERPsl/fMe+G99I/9r/43P7ku9b225ynbCH/+G90py9g=</latexit> <latexit sha1_base64="eY4cuuNdtPSoc87X0TvZnXEtJMc=">AAACsXicdVFtaxNBEN4732p8S6vfRBlMlZRiuCuFVopS8IsfKyS2mDvi3t5csmRv79idk4Qj3/2L/gl/g3vpCSbVgV0enpl5ZvbZpFTSUhD89Pxbt+/cvbdzv/Pg4aPHT7q7e19sURmBI1Gowlwl3KKSGkckSeFVaZDnicLLZP6xyV9+R2NloYe0LDHO+VTLTApOjpp0fwz7+gCiM3jfXJ0owanUtXCKdtWJzqLhDIn3wwN4AxHhgmqQGexrVx7uwwqiaDw4wTx2pUdOCd5C2KgdOi34b++HP72dCHXaDpt0e8EgWAfcBGELeqyNi8mutxelhahy1CQUt3YcBiXFNTckhUK3fWWx5GLOpzh2UPMcbVyvLVvBa8ekkBXGHU2wZv/uqHlu7TJPXGXOaWa3cw35r9y4ouw0rqUuK0ItrgdllQIqoPEfUmlQkFo6wIWRblcQM264IPdLG1PW2iWKjZfUi0pLUaS4xSpakOGNi+G2ZzfB6GjwbhB+Pu6dn7Z27rDn7BXrs5CdsHP2iV2wERPsl/fMe+G99I/9r/43P7ku9b225ynbCH/+G90py9g=</latexit> <latexit sha1_base64="eY4cuuNdtPSoc87X0TvZnXEtJMc=">AAACsXicdVFtaxNBEN4732p8S6vfRBlMlZRiuCuFVopS8IsfKyS2mDvi3t5csmRv79idk4Qj3/2L/gl/g3vpCSbVgV0enpl5ZvbZpFTSUhD89Pxbt+/cvbdzv/Pg4aPHT7q7e19sURmBI1Gowlwl3KKSGkckSeFVaZDnicLLZP6xyV9+R2NloYe0LDHO+VTLTApOjpp0fwz7+gCiM3jfXJ0owanUtXCKdtWJzqLhDIn3wwN4AxHhgmqQGexrVx7uwwqiaDw4wTx2pUdOCd5C2KgdOi34b++HP72dCHXaDpt0e8EgWAfcBGELeqyNi8mutxelhahy1CQUt3YcBiXFNTckhUK3fWWx5GLOpzh2UPMcbVyvLVvBa8ekkBXGHU2wZv/uqHlu7TJPXGXOaWa3cw35r9y4ouw0rqUuK0ItrgdllQIqoPEfUmlQkFo6wIWRblcQM264IPdLG1PW2iWKjZfUi0pLUaS4xSpakOGNi+G2ZzfB6GjwbhB+Pu6dn7Z27rDn7BXrs5CdsHP2iV2wERPsl/fMe+G99I/9r/43P7ku9b225ynbCH/+G90py9g=</latexit>
- 13. Weighted interval scheduling: brute force Observation. Recursive algorithm is spectacularly slow because of overlapping subproblems ⇒ exponential-time algorithm. Ex. Number of recursive calls for family of “layered” instances grows like Fibonacci sequence. 13 3 4 5 1 2 p(1) = 0, p(j) = j-2 4 3 3 2 2 1 2 1 1 0 1 0 1 0 recursion tree 5
- 14. Weighted interval scheduling: memoization Top-down dynamic programming (memoization). ・Cache result of subproblem j in M[j]. ・Use M[j] to avoid solving subproblem j more than once. 14 M-COMPUTE-OPT( j ) _________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ IF (M[j] is uninitialized) M[j] ← max { M-COMPUTE-OPT (j – 1), wj + M-COMPUTE-OPT(p[j]) }. RETURN M[j]. TOP-DOWN(n, s1, …, sn, f1, …, fn, w1, …, wn) _________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Sort jobs by finish time and renumber so that f1 ≤ f2 ≤ … ≤ fn. Compute p[1], p[2], …, p[n] via binary search. M[0] ← 0. RETURN M-COMPUTE-OPT(n). global array
- 15. Weighted interval scheduling: running time Claim. Memoized version of algorithm takes O(n log n) time. Pf. ・Sort by finish time: O(n log n) via mergesort. ・Compute p[j] for each j : O(n log n) via binary search. ・M-COMPUTE-OPT(j): each invocation takes O(1) time and either - (1) returns an initialized value M[j] - (2) initializes M[j] and makes two recursive calls ・Progress measure Φ = # initialized entries among M[1.. n]. - initially Φ = 0; throughout Φ ≤ n. - (2) increases Φ by 1 ⇒ ≤ 2n recursive calls. ・Overall running time of M-COMPUTE-OPT(n) is O(n). ▪ 15
- 16. 16
- 17. Weighted interval scheduling: finding a solution Q. DP algorithm computes optimal value. How to find optimal solution? A. Make a second pass by calling FIND-SOLUTION(n). Analysis. # of recursive calls ≤ n ⇒ O(n). 17 FIND-SOLUTION(j) _____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ ____________________________________________________________________________________________________________ IF (j = 0) RETURN ∅. ELSE IF (wj + M[p[j]] > M[ j – 1]) RETURN { j } ∪ FIND-SOLUTION(p[j]). ELSE RETURN FIND-SOLUTION( j – 1). M[j] = max { M[j – 1], wj + M[p[j]] }.
- 18. Weighted interval scheduling: bottom-up dynamic programming Bottom-up dynamic programming. Unwind recursion. Running time. The bottom-up version takes O(n log n) time. 18 BOTTOM-UP(n, s1, …, sn, f1, …, fn, w1, …, wn) _________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Sort jobs by finish time and renumber so that f1 ≤ f2 ≤ … ≤ fn. Compute p[1], p[2], …, p[n]. M[0] ← 0. FOR j = 1 TO n M[j] ← max { M[ j – 1], wj + M[p[j]] }. _________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ previously computed values
- 19. MAXIMUM SUBARRAY PROBLEM Goal. Given an array x of n integer (positive or negative), find a contiguous subarray whose sum is maximum. Applications. Computer vision, data mining, genomic sequence analysis, technical job interviews, …. 19 12 5 −1 31 −61 59 26 −53 58 97 −93 −23 84 −15 6 187
- 20. MAXIMUM SUBARRAY PROBLEM Goal. Given an array x of n integer (positive or negative), find a contiguous subarray whose sum is maximum. Brute-force algorithm. ・For each i and j : computer a[i] + a[i+1] + … + a[j]. ・Takes Θ(n3 ) time. Apply “cumulative sum” trick. ・Precompute cumulative sums: S[i] = a[0] + a[1] + … + a[i]. ・Now a[i] + a[i+1] + … + a[j] = S[j] − S[i−1]. ・Improves running time Θ(n2 ). 20 12 5 −1 31 −61 59 26 −53 58 97 −93 −23 84 −15 6 187 i j
- 21. KADANE’S ALGORITHM Def. OPT(i) = max sum of any subarray of x whose rightmost index is i. Goal. Bellman equation. Running time. O(n). 21 take only element i take element i together with best subarray ending at index i − 1 OPT(i) = x1 B7 i = 1 max { xi, xi + OPT(i 1) } B7 i > 1 <latexit sha1_base64="IzPr6CPzgLq87qXSEs8B8qojGEU=">AAACwnicbVFdb9MwFHXC1yhf3Xjk5YpqaBOjawCJoWpoEkLijSKtbFIdRY5z01p1nGA7KFXoD+Gn8WvAyfJAW65k+eice8/1vY4LKYwdjX57/q3bd+7e27vfe/Dw0eMn/f2DbyYvNccpz2Wur2NmUAqFUyusxOtCI8tiiVfx8mOjX/1AbUSuLu2qwDBjcyVSwZl1VNT/9WVyeSSOgY7P6bhHY5wLVXNnaNY9Oq6iAF4AtVhZqEGksAYB5xAApbPhG8xCl0MzVgGVmFqgNdATqCJx4vyaG15C6/8qOG4UqsV84dLWu6YfWtMeRZV07aP+YDQctQG7IOjAgHQxifa9A5rkvMxQWS6ZMbNgVNiwZtoKLtHNUxosGF+yOc4cVCxDE9btDtdw6JgE0ly7oyy07L8VNcuMWWWxy8yYXZhtrSH/p81Km56FtVBFaVHxm0ZpKcHm0HwIJEIjt3LlAONauLcCXzDNuHXfttGl9S6Qb0xSV6USPE9wi5W2spo1Wwy2d7YLpq+H74fB17eDi7NunXvkGXlOjkhA3pEL8plMyJRw8sc79Ibeqf/JX/rffXOT6ntdzVOyEf7Pv+19094=</latexit> <latexit sha1_base64="IzPr6CPzgLq87qXSEs8B8qojGEU=">AAACwnicbVFdb9MwFHXC1yhf3Xjk5YpqaBOjawCJoWpoEkLijSKtbFIdRY5z01p1nGA7KFXoD+Gn8WvAyfJAW65k+eice8/1vY4LKYwdjX57/q3bd+7e27vfe/Dw0eMn/f2DbyYvNccpz2Wur2NmUAqFUyusxOtCI8tiiVfx8mOjX/1AbUSuLu2qwDBjcyVSwZl1VNT/9WVyeSSOgY7P6bhHY5wLVXNnaNY9Oq6iAF4AtVhZqEGksAYB5xAApbPhG8xCl0MzVgGVmFqgNdATqCJx4vyaG15C6/8qOG4UqsV84dLWu6YfWtMeRZV07aP+YDQctQG7IOjAgHQxifa9A5rkvMxQWS6ZMbNgVNiwZtoKLtHNUxosGF+yOc4cVCxDE9btDtdw6JgE0ly7oyy07L8VNcuMWWWxy8yYXZhtrSH/p81Km56FtVBFaVHxm0ZpKcHm0HwIJEIjt3LlAONauLcCXzDNuHXfttGl9S6Qb0xSV6USPE9wi5W2spo1Wwy2d7YLpq+H74fB17eDi7NunXvkGXlOjkhA3pEL8plMyJRw8sc79Ibeqf/JX/rffXOT6ntdzVOyEf7Pv+19094=</latexit> <latexit sha1_base64="IzPr6CPzgLq87qXSEs8B8qojGEU=">AAACwnicbVFdb9MwFHXC1yhf3Xjk5YpqaBOjawCJoWpoEkLijSKtbFIdRY5z01p1nGA7KFXoD+Gn8WvAyfJAW65k+eice8/1vY4LKYwdjX57/q3bd+7e27vfe/Dw0eMn/f2DbyYvNccpz2Wur2NmUAqFUyusxOtCI8tiiVfx8mOjX/1AbUSuLu2qwDBjcyVSwZl1VNT/9WVyeSSOgY7P6bhHY5wLVXNnaNY9Oq6iAF4AtVhZqEGksAYB5xAApbPhG8xCl0MzVgGVmFqgNdATqCJx4vyaG15C6/8qOG4UqsV84dLWu6YfWtMeRZV07aP+YDQctQG7IOjAgHQxifa9A5rkvMxQWS6ZMbNgVNiwZtoKLtHNUxosGF+yOc4cVCxDE9btDtdw6JgE0ly7oyy07L8VNcuMWWWxy8yYXZhtrSH/p81Km56FtVBFaVHxm0ZpKcHm0HwIJEIjt3LlAONauLcCXzDNuHXfttGl9S6Qb0xSV6USPE9wi5W2spo1Wwy2d7YLpq+H74fB17eDi7NunXvkGXlOjkhA3pEL8plMyJRw8sc79Ibeqf/JX/rffXOT6ntdzVOyEf7Pv+19094=</latexit> <latexit sha1_base64="IzPr6CPzgLq87qXSEs8B8qojGEU=">AAACwnicbVFdb9MwFHXC1yhf3Xjk5YpqaBOjawCJoWpoEkLijSKtbFIdRY5z01p1nGA7KFXoD+Gn8WvAyfJAW65k+eice8/1vY4LKYwdjX57/q3bd+7e27vfe/Dw0eMn/f2DbyYvNccpz2Wur2NmUAqFUyusxOtCI8tiiVfx8mOjX/1AbUSuLu2qwDBjcyVSwZl1VNT/9WVyeSSOgY7P6bhHY5wLVXNnaNY9Oq6iAF4AtVhZqEGksAYB5xAApbPhG8xCl0MzVgGVmFqgNdATqCJx4vyaG15C6/8qOG4UqsV84dLWu6YfWtMeRZV07aP+YDQctQG7IOjAgHQxifa9A5rkvMxQWS6ZMbNgVNiwZtoKLtHNUxosGF+yOc4cVCxDE9btDtdw6JgE0ly7oyy07L8VNcuMWWWxy8yYXZhtrSH/p81Km56FtVBFaVHxm0ZpKcHm0HwIJEIjt3LlAONauLcCXzDNuHXfttGl9S6Qb0xSV6USPE9wi5W2spo1Wwy2d7YLpq+H74fB17eDi7NunXvkGXlOjkhA3pEL8plMyJRw8sc79Ibeqf/JX/rffXOT6ntdzVOyEf7Pv+19094=</latexit> max i OPT(i) <latexit sha1_base64="CZcWtyZJDhy3Lko1sMUcUMz99YY=">AAACOXicbVDLTgIxFO3gC/E14NJNIzHRDZkxJmLckLhxJyYgJEBIp1y0odOZtHcIZMKfuNWv8EfcujJu/QHLYyHoSZqcnHNfPUEshUHPe3cya+sbm1vZ7dzO7t7+gZsvPJgo0RzqPJKRbgbMgBQK6ihQQjPWwMJAQiMY3Ez9xhC0EZGq4TiGTsgelegLztBKXddth2zUFbR9Te+qtVNx1nWLXsmbgf4l/oIUyQLVbt4ptHsRT0JQyCUzpuV7MXZSplFwCZNcOzEQMz5gj9CyVLEQTCednT6hJ1bp0X6k7VNIZ+rvjpSFxozDwFaGDJ/MqjcV//NaCfbLnVSoOEFQfL6on0iKEZ3mQHtCA0c5toRxLeytlD8xzTjatJa2zGbHwJd+ko4SJXjUgxVV4gg1m9gU/dXM/pL6eemq5N9fFCvlRZxZckSOySnxySWpkFtSJXXCyZA8kxfy6rw5H86n8zUvzTiLnkOyBOf7B0NwrLA=</latexit> <latexit sha1_base64="CZcWtyZJDhy3Lko1sMUcUMz99YY=">AAACOXicbVDLTgIxFO3gC/E14NJNIzHRDZkxJmLckLhxJyYgJEBIp1y0odOZtHcIZMKfuNWv8EfcujJu/QHLYyHoSZqcnHNfPUEshUHPe3cya+sbm1vZ7dzO7t7+gZsvPJgo0RzqPJKRbgbMgBQK6ihQQjPWwMJAQiMY3Ez9xhC0EZGq4TiGTsgelegLztBKXddth2zUFbR9Te+qtVNx1nWLXsmbgf4l/oIUyQLVbt4ptHsRT0JQyCUzpuV7MXZSplFwCZNcOzEQMz5gj9CyVLEQTCednT6hJ1bp0X6k7VNIZ+rvjpSFxozDwFaGDJ/MqjcV//NaCfbLnVSoOEFQfL6on0iKEZ3mQHtCA0c5toRxLeytlD8xzTjatJa2zGbHwJd+ko4SJXjUgxVV4gg1m9gU/dXM/pL6eemq5N9fFCvlRZxZckSOySnxySWpkFtSJXXCyZA8kxfy6rw5H86n8zUvzTiLnkOyBOf7B0NwrLA=</latexit> <latexit sha1_base64="CZcWtyZJDhy3Lko1sMUcUMz99YY=">AAACOXicbVDLTgIxFO3gC/E14NJNIzHRDZkxJmLckLhxJyYgJEBIp1y0odOZtHcIZMKfuNWv8EfcujJu/QHLYyHoSZqcnHNfPUEshUHPe3cya+sbm1vZ7dzO7t7+gZsvPJgo0RzqPJKRbgbMgBQK6ihQQjPWwMJAQiMY3Ez9xhC0EZGq4TiGTsgelegLztBKXddth2zUFbR9Te+qtVNx1nWLXsmbgf4l/oIUyQLVbt4ptHsRT0JQyCUzpuV7MXZSplFwCZNcOzEQMz5gj9CyVLEQTCednT6hJ1bp0X6k7VNIZ+rvjpSFxozDwFaGDJ/MqjcV//NaCfbLnVSoOEFQfL6on0iKEZ3mQHtCA0c5toRxLeytlD8xzTjatJa2zGbHwJd+ko4SJXjUgxVV4gg1m9gU/dXM/pL6eemq5N9fFCvlRZxZckSOySnxySWpkFtSJXXCyZA8kxfy6rw5H86n8zUvzTiLnkOyBOf7B0NwrLA=</latexit> <latexit sha1_base64="CZcWtyZJDhy3Lko1sMUcUMz99YY=">AAACOXicbVDLTgIxFO3gC/E14NJNIzHRDZkxJmLckLhxJyYgJEBIp1y0odOZtHcIZMKfuNWv8EfcujJu/QHLYyHoSZqcnHNfPUEshUHPe3cya+sbm1vZ7dzO7t7+gZsvPJgo0RzqPJKRbgbMgBQK6ihQQjPWwMJAQiMY3Ez9xhC0EZGq4TiGTsgelegLztBKXddth2zUFbR9Te+qtVNx1nWLXsmbgf4l/oIUyQLVbt4ptHsRT0JQyCUzpuV7MXZSplFwCZNcOzEQMz5gj9CyVLEQTCednT6hJ1bp0X6k7VNIZ+rvjpSFxozDwFaGDJ/MqjcV//NaCfbLnVSoOEFQfL6on0iKEZ3mQHtCA0c5toRxLeytlD8xzTjatJa2zGbHwJd+ko4SJXjUgxVV4gg1m9gU/dXM/pL6eemq5N9fFCvlRZxZckSOySnxySWpkFtSJXXCyZA8kxfy6rw5H86n8zUvzTiLnkOyBOf7B0NwrLA=</latexit>
- 22. Goal. Given an n-by-n matrix A, find a rectangle whose sum is maximum. Applications. Databases, image processing, maximum likelihood estimation, technical job interviews, … A = 2 5 0 5 2 2 3 4 3 1 3 2 1 1 5 6 3 5 1 4 2 1 1 3 1 4 1 1 3 3 2 0 3 3 2 2 1 2 1 1 3 1 2 4 0 1 0 3 1 <latexit sha1_base64="7MCCgMPkRZ+McrhVixdB+YGxHPQ=">AAADhXicbVLbbtNAEF3XQEu4teWRlxERiJdEdmJKJYQo4oXHIpG2Iraq9WaSrLpeW7tr1MjKx/EZfAGv8AesvbmXkXZ0dObMmfV400JwbYLgl7fn37v/YP/gYevR4ydPnx0eHV/ovFQMBywXubpKqUbBJQ4MNwKvCoU0SwVepjef6/rlD1Sa5/KbmRWYZHQi+Zgzaix1feR9/wTxe/hQp1jg2MAQ4hQnXFZUKTqbV8rFvNXpwWuAt3UKbOrUyHF16vQhjofdCLOkBZEjbArren8pgtBxK2VjAidLkfNsRJFzXyvDLTuHoqUnbHi6+npmsOrp73qu79TbcFqPWHv2lndyduFqC07ZilGOFhtrxYpPpgaS68N20A2agLsgXIA2WcS5/RvH8ShnZYbSMEG1HoZBYRLrazgTaJ1LjQVlN3SCQwslzVAnVfMK5vDKMiMY58oeaaBhNzsqmmk9y1KrzKiZ6t1aTf6vNizN+DSpuCxKg5K5QeNSgMmhflIw4gqZETMLKFPc3hXYlCrKjH14W1Ma7wLZ1pdUt6XkLB/hDivMrVF0brcY7u7sLrjodUO72q9R++x0sc8D8oK8JG9ISN6RM/KFnJMBYd5P77f3x/vr7/sdP/JPnHTPW/Q8J1vhf/wHS3ruiw==</latexit> <latexit sha1_base64="7MCCgMPkRZ+McrhVixdB+YGxHPQ=">AAADhXicbVLbbtNAEF3XQEu4teWRlxERiJdEdmJKJYQo4oXHIpG2Iraq9WaSrLpeW7tr1MjKx/EZfAGv8AesvbmXkXZ0dObMmfV400JwbYLgl7fn37v/YP/gYevR4ydPnx0eHV/ovFQMBywXubpKqUbBJQ4MNwKvCoU0SwVepjef6/rlD1Sa5/KbmRWYZHQi+Zgzaix1feR9/wTxe/hQp1jg2MAQ4hQnXFZUKTqbV8rFvNXpwWuAt3UKbOrUyHF16vQhjofdCLOkBZEjbArren8pgtBxK2VjAidLkfNsRJFzXyvDLTuHoqUnbHi6+npmsOrp73qu79TbcFqPWHv2lndyduFqC07ZilGOFhtrxYpPpgaS68N20A2agLsgXIA2WcS5/RvH8ShnZYbSMEG1HoZBYRLrazgTaJ1LjQVlN3SCQwslzVAnVfMK5vDKMiMY58oeaaBhNzsqmmk9y1KrzKiZ6t1aTf6vNizN+DSpuCxKg5K5QeNSgMmhflIw4gqZETMLKFPc3hXYlCrKjH14W1Ma7wLZ1pdUt6XkLB/hDivMrVF0brcY7u7sLrjodUO72q9R++x0sc8D8oK8JG9ISN6RM/KFnJMBYd5P77f3x/vr7/sdP/JPnHTPW/Q8J1vhf/wHS3ruiw==</latexit> <latexit sha1_base64="7MCCgMPkRZ+McrhVixdB+YGxHPQ=">AAADhXicbVLbbtNAEF3XQEu4teWRlxERiJdEdmJKJYQo4oXHIpG2Iraq9WaSrLpeW7tr1MjKx/EZfAGv8AesvbmXkXZ0dObMmfV400JwbYLgl7fn37v/YP/gYevR4ydPnx0eHV/ovFQMBywXubpKqUbBJQ4MNwKvCoU0SwVepjef6/rlD1Sa5/KbmRWYZHQi+Zgzaix1feR9/wTxe/hQp1jg2MAQ4hQnXFZUKTqbV8rFvNXpwWuAt3UKbOrUyHF16vQhjofdCLOkBZEjbArren8pgtBxK2VjAidLkfNsRJFzXyvDLTuHoqUnbHi6+npmsOrp73qu79TbcFqPWHv2lndyduFqC07ZilGOFhtrxYpPpgaS68N20A2agLsgXIA2WcS5/RvH8ShnZYbSMEG1HoZBYRLrazgTaJ1LjQVlN3SCQwslzVAnVfMK5vDKMiMY58oeaaBhNzsqmmk9y1KrzKiZ6t1aTf6vNizN+DSpuCxKg5K5QeNSgMmhflIw4gqZETMLKFPc3hXYlCrKjH14W1Ma7wLZ1pdUt6XkLB/hDivMrVF0brcY7u7sLrjodUO72q9R++x0sc8D8oK8JG9ISN6RM/KFnJMBYd5P77f3x/vr7/sdP/JPnHTPW/Q8J1vhf/wHS3ruiw==</latexit> <latexit sha1_base64="7MCCgMPkRZ+McrhVixdB+YGxHPQ=">AAADhXicbVLbbtNAEF3XQEu4teWRlxERiJdEdmJKJYQo4oXHIpG2Iraq9WaSrLpeW7tr1MjKx/EZfAGv8AesvbmXkXZ0dObMmfV400JwbYLgl7fn37v/YP/gYevR4ydPnx0eHV/ovFQMBywXubpKqUbBJQ4MNwKvCoU0SwVepjef6/rlD1Sa5/KbmRWYZHQi+Zgzaix1feR9/wTxe/hQp1jg2MAQ4hQnXFZUKTqbV8rFvNXpwWuAt3UKbOrUyHF16vQhjofdCLOkBZEjbArren8pgtBxK2VjAidLkfNsRJFzXyvDLTuHoqUnbHi6+npmsOrp73qu79TbcFqPWHv2lndyduFqC07ZilGOFhtrxYpPpgaS68N20A2agLsgXIA2WcS5/RvH8ShnZYbSMEG1HoZBYRLrazgTaJ1LjQVlN3SCQwslzVAnVfMK5vDKMiMY58oeaaBhNzsqmmk9y1KrzKiZ6t1aTf6vNizN+DSpuCxKg5K5QeNSgMmhflIw4gqZETMLKFPc3hXYlCrKjH14W1Ma7wLZ1pdUt6XkLB/hDivMrVF0brcY7u7sLrjodUO72q9R++x0sc8D8oK8JG9ISN6RM/KFnJMBYd5P77f3x/vr7/sdP/JPnHTPW/Q8J1vhf/wHS3ruiw==</latexit> MAXIMUM RECTANGLE PROBLEM 22 13
- 23. j jʹ Assumption. Suppose you knew the left and right column indices j and jʹ. An O(n3 ) algorithm. ・Precompute cumulative row sums . ・For each j < jʹ : – define array x using row-sum differences: – run Kadane’s algorithm in array x Open problem. O(n3−ε ) for any constant ε > 0. A = 2 5 0 5 2 2 3 4 3 1 3 2 1 1 5 6 3 5 1 4 2 1 1 3 1 4 1 1 3 3 2 0 3 3 2 2 1 2 1 1 3 1 2 4 0 1 0 3 1 <latexit sha1_base64="7MCCgMPkRZ+McrhVixdB+YGxHPQ=">AAADhXicbVLbbtNAEF3XQEu4teWRlxERiJdEdmJKJYQo4oXHIpG2Iraq9WaSrLpeW7tr1MjKx/EZfAGv8AesvbmXkXZ0dObMmfV400JwbYLgl7fn37v/YP/gYevR4ydPnx0eHV/ovFQMBywXubpKqUbBJQ4MNwKvCoU0SwVepjef6/rlD1Sa5/KbmRWYZHQi+Zgzaix1feR9/wTxe/hQp1jg2MAQ4hQnXFZUKTqbV8rFvNXpwWuAt3UKbOrUyHF16vQhjofdCLOkBZEjbArren8pgtBxK2VjAidLkfNsRJFzXyvDLTuHoqUnbHi6+npmsOrp73qu79TbcFqPWHv2lndyduFqC07ZilGOFhtrxYpPpgaS68N20A2agLsgXIA2WcS5/RvH8ShnZYbSMEG1HoZBYRLrazgTaJ1LjQVlN3SCQwslzVAnVfMK5vDKMiMY58oeaaBhNzsqmmk9y1KrzKiZ6t1aTf6vNizN+DSpuCxKg5K5QeNSgMmhflIw4gqZETMLKFPc3hXYlCrKjH14W1Ma7wLZ1pdUt6XkLB/hDivMrVF0brcY7u7sLrjodUO72q9R++x0sc8D8oK8JG9ISN6RM/KFnJMBYd5P77f3x/vr7/sdP/JPnHTPW/Q8J1vhf/wHS3ruiw==</latexit> <latexit sha1_base64="7MCCgMPkRZ+McrhVixdB+YGxHPQ=">AAADhXicbVLbbtNAEF3XQEu4teWRlxERiJdEdmJKJYQo4oXHIpG2Iraq9WaSrLpeW7tr1MjKx/EZfAGv8AesvbmXkXZ0dObMmfV400JwbYLgl7fn37v/YP/gYevR4ydPnx0eHV/ovFQMBywXubpKqUbBJQ4MNwKvCoU0SwVepjef6/rlD1Sa5/KbmRWYZHQi+Zgzaix1feR9/wTxe/hQp1jg2MAQ4hQnXFZUKTqbV8rFvNXpwWuAt3UKbOrUyHF16vQhjofdCLOkBZEjbArren8pgtBxK2VjAidLkfNsRJFzXyvDLTuHoqUnbHi6+npmsOrp73qu79TbcFqPWHv2lndyduFqC07ZilGOFhtrxYpPpgaS68N20A2agLsgXIA2WcS5/RvH8ShnZYbSMEG1HoZBYRLrazgTaJ1LjQVlN3SCQwslzVAnVfMK5vDKMiMY58oeaaBhNzsqmmk9y1KrzKiZ6t1aTf6vNizN+DSpuCxKg5K5QeNSgMmhflIw4gqZETMLKFPc3hXYlCrKjH14W1Ma7wLZ1pdUt6XkLB/hDivMrVF0brcY7u7sLrjodUO72q9R++x0sc8D8oK8JG9ISN6RM/KFnJMBYd5P77f3x/vr7/sdP/JPnHTPW/Q8J1vhf/wHS3ruiw==</latexit> <latexit sha1_base64="7MCCgMPkRZ+McrhVixdB+YGxHPQ=">AAADhXicbVLbbtNAEF3XQEu4teWRlxERiJdEdmJKJYQo4oXHIpG2Iraq9WaSrLpeW7tr1MjKx/EZfAGv8AesvbmXkXZ0dObMmfV400JwbYLgl7fn37v/YP/gYevR4ydPnx0eHV/ovFQMBywXubpKqUbBJQ4MNwKvCoU0SwVepjef6/rlD1Sa5/KbmRWYZHQi+Zgzaix1feR9/wTxe/hQp1jg2MAQ4hQnXFZUKTqbV8rFvNXpwWuAt3UKbOrUyHF16vQhjofdCLOkBZEjbArren8pgtBxK2VjAidLkfNsRJFzXyvDLTuHoqUnbHi6+npmsOrp73qu79TbcFqPWHv2lndyduFqC07ZilGOFhtrxYpPpgaS68N20A2agLsgXIA2WcS5/RvH8ShnZYbSMEG1HoZBYRLrazgTaJ1LjQVlN3SCQwslzVAnVfMK5vDKMiMY58oeaaBhNzsqmmk9y1KrzKiZ6t1aTf6vNizN+DSpuCxKg5K5QeNSgMmhflIw4gqZETMLKFPc3hXYlCrKjH14W1Ma7wLZ1pdUt6XkLB/hDivMrVF0brcY7u7sLrjodUO72q9R++x0sc8D8oK8JG9ISN6RM/KFnJMBYd5P77f3x/vr7/sdP/JPnHTPW/Q8J1vhf/wHS3ruiw==</latexit> <latexit sha1_base64="7MCCgMPkRZ+McrhVixdB+YGxHPQ=">AAADhXicbVLbbtNAEF3XQEu4teWRlxERiJdEdmJKJYQo4oXHIpG2Iraq9WaSrLpeW7tr1MjKx/EZfAGv8AesvbmXkXZ0dObMmfV400JwbYLgl7fn37v/YP/gYevR4ydPnx0eHV/ovFQMBywXubpKqUbBJQ4MNwKvCoU0SwVepjef6/rlD1Sa5/KbmRWYZHQi+Zgzaix1feR9/wTxe/hQp1jg2MAQ4hQnXFZUKTqbV8rFvNXpwWuAt3UKbOrUyHF16vQhjofdCLOkBZEjbArren8pgtBxK2VjAidLkfNsRJFzXyvDLTuHoqUnbHi6+npmsOrp73qu79TbcFqPWHv2lndyduFqC07ZilGOFhtrxYpPpgaS68N20A2agLsgXIA2WcS5/RvH8ShnZYbSMEG1HoZBYRLrazgTaJ1LjQVlN3SCQwslzVAnVfMK5vDKMiMY58oeaaBhNzsqmmk9y1KrzKiZ6t1aTf6vNizN+DSpuCxKg5K5QeNSgMmhflIw4gqZETMLKFPc3hXYlCrKjH14W1Ma7wLZ1pdUt6XkLB/hDivMrVF0brcY7u7sLrjodUO72q9R++x0sc8D8oK8JG9ISN6RM/KFnJMBYd5P77f3x/vr7/sdP/JPnHTPW/Q8J1vhf/wHS3ruiw==</latexit> BENTLEY’S ALGORITHM 23 Sij = j k = 1 Aik <latexit sha1_base64="hAhGMhRyRjoYbIVIbkUh6Iy0kU0=">AAACUHicbVDBThsxEJ0N0NIAJcCxF4sIlQOKdqtK0AMSFReOVG0AKZuuvM4ETGzvyp6tiFb7CXwNV/gKTnwKJ+qEIJHAkyw/vTfj8bw0V9JRGD4Etbn5hQ8fFz/Vl5ZXPq821tZPXFZYgW2RqcyepdyhkgbbJEnhWW6R61ThaTo4HPmn/9A6mZk/NMyxq/m5kX0pOHkpaXz9nZTysmL7LHaFjpXUklxSDuKd/Xgnqv5esp++YFAljWbYCsdgb0k0IU2Y4DhZC9bjXiYKjYaE4s51ojCnbsktSaGwqseFw5yLAT/HjqeGa3TdcrxRxba80mP9zPpjiI3V1x0l184NdeorNacLN+uNxPe8TkH9vW4pTV4QGvE8qF8oRhkbxcN60qIgNfSECyv9X5m44JYL8iFOTRm/naOY2qS8KowUWQ9nVEVXZPkoxWg2s7ek/a31oxX9+t482JvEuQhfYBO2IYJdOIAjOIY2CLiGG7iFu+A+eAyeasFz6csNGzCFWv0/uUC01w==</latexit> <latexit sha1_base64="hAhGMhRyRjoYbIVIbkUh6Iy0kU0=">AAACUHicbVDBThsxEJ0N0NIAJcCxF4sIlQOKdqtK0AMSFReOVG0AKZuuvM4ETGzvyp6tiFb7CXwNV/gKTnwKJ+qEIJHAkyw/vTfj8bw0V9JRGD4Etbn5hQ8fFz/Vl5ZXPq821tZPXFZYgW2RqcyepdyhkgbbJEnhWW6R61ThaTo4HPmn/9A6mZk/NMyxq/m5kX0pOHkpaXz9nZTysmL7LHaFjpXUklxSDuKd/Xgnqv5esp++YFAljWbYCsdgb0k0IU2Y4DhZC9bjXiYKjYaE4s51ojCnbsktSaGwqseFw5yLAT/HjqeGa3TdcrxRxba80mP9zPpjiI3V1x0l184NdeorNacLN+uNxPe8TkH9vW4pTV4QGvE8qF8oRhkbxcN60qIgNfSECyv9X5m44JYL8iFOTRm/naOY2qS8KowUWQ9nVEVXZPkoxWg2s7ek/a31oxX9+t482JvEuQhfYBO2IYJdOIAjOIY2CLiGG7iFu+A+eAyeasFz6csNGzCFWv0/uUC01w==</latexit> <latexit sha1_base64="hAhGMhRyRjoYbIVIbkUh6Iy0kU0=">AAACUHicbVDBThsxEJ0N0NIAJcCxF4sIlQOKdqtK0AMSFReOVG0AKZuuvM4ETGzvyp6tiFb7CXwNV/gKTnwKJ+qEIJHAkyw/vTfj8bw0V9JRGD4Etbn5hQ8fFz/Vl5ZXPq821tZPXFZYgW2RqcyepdyhkgbbJEnhWW6R61ThaTo4HPmn/9A6mZk/NMyxq/m5kX0pOHkpaXz9nZTysmL7LHaFjpXUklxSDuKd/Xgnqv5esp++YFAljWbYCsdgb0k0IU2Y4DhZC9bjXiYKjYaE4s51ojCnbsktSaGwqseFw5yLAT/HjqeGa3TdcrxRxba80mP9zPpjiI3V1x0l184NdeorNacLN+uNxPe8TkH9vW4pTV4QGvE8qF8oRhkbxcN60qIgNfSECyv9X5m44JYL8iFOTRm/naOY2qS8KowUWQ9nVEVXZPkoxWg2s7ek/a31oxX9+t482JvEuQhfYBO2IYJdOIAjOIY2CLiGG7iFu+A+eAyeasFz6csNGzCFWv0/uUC01w==</latexit> <latexit sha1_base64="hAhGMhRyRjoYbIVIbkUh6Iy0kU0=">AAACUHicbVDBThsxEJ0N0NIAJcCxF4sIlQOKdqtK0AMSFReOVG0AKZuuvM4ETGzvyp6tiFb7CXwNV/gKTnwKJ+qEIJHAkyw/vTfj8bw0V9JRGD4Etbn5hQ8fFz/Vl5ZXPq821tZPXFZYgW2RqcyepdyhkgbbJEnhWW6R61ThaTo4HPmn/9A6mZk/NMyxq/m5kX0pOHkpaXz9nZTysmL7LHaFjpXUklxSDuKd/Xgnqv5esp++YFAljWbYCsdgb0k0IU2Y4DhZC9bjXiYKjYaE4s51ojCnbsktSaGwqseFw5yLAT/HjqeGa3TdcrxRxba80mP9zPpjiI3V1x0l184NdeorNacLN+uNxPe8TkH9vW4pTV4QGvE8qF8oRhkbxcN60qIgNfSECyv9X5m44JYL8iFOTRm/naOY2qS8KowUWQ9nVEVXZPkoxWg2s7ek/a31oxX9+t482JvEuQhfYBO2IYJdOIAjOIY2CLiGG7iFu+A+eAyeasFz6csNGzCFWv0/uUC01w==</latexit> solve maximum subarray problem in this array x = 7 4 3 6 5 0 1 <latexit sha1_base64="KksKdRyhI0qOgtDRpYhf7ThpXdA=">AAACrnicbVHRatswFJXdrUvdrUvSt/ZFLBT20mB32doyBoW+7LGDZSnYJsjydSIqy0a6Hgkmj/3IfsN+YkpqmJPugsTRufeeKx0lpRQGff/Jcfdevd5/0znwDt++O3rf7fV/maLSHMa8kIW+T5gBKRSMUaCE+1IDyxMJk+Thdp2f/AZtRKF+4rKEOGczJTLBGVpq2n1c0Ogr/bbevEhChjSkUQIzoWqmNVuuar3yzi9pFIXDEeSxR0f/8PmnFv+lhT/T1sFvHwIvApU22l6kxWyONJ52B/7Q3wR9CYIGDEgTd9Oe04/Sglc5KOSSGRMGfomx1UXBJVjlykDJ+AObQWihYjmYuN74taJnlklpVmi7FNIN2+6oWW7MMk9sZc5wbnZza/J/ubDC7CquhSorBMWfB2WVpFjQtfk0FRo4yqUFjGth70r5nGnG0X7R1pSNdgl86yX1olKCFynssBIXqNnKuhjsevYSjC+G18Pgx2hwc9XY2SGn5AP5SAJySW7Id3JHxoSTP07POXFO3cCduLE7fS51nabnmGyFO/8L1OHLhA==</latexit> <latexit sha1_base64="KksKdRyhI0qOgtDRpYhf7ThpXdA=">AAACrnicbVHRatswFJXdrUvdrUvSt/ZFLBT20mB32doyBoW+7LGDZSnYJsjydSIqy0a6Hgkmj/3IfsN+YkpqmJPugsTRufeeKx0lpRQGff/Jcfdevd5/0znwDt++O3rf7fV/maLSHMa8kIW+T5gBKRSMUaCE+1IDyxMJk+Thdp2f/AZtRKF+4rKEOGczJTLBGVpq2n1c0Ogr/bbevEhChjSkUQIzoWqmNVuuar3yzi9pFIXDEeSxR0f/8PmnFv+lhT/T1sFvHwIvApU22l6kxWyONJ52B/7Q3wR9CYIGDEgTd9Oe04/Sglc5KOSSGRMGfomx1UXBJVjlykDJ+AObQWihYjmYuN74taJnlklpVmi7FNIN2+6oWW7MMk9sZc5wbnZza/J/ubDC7CquhSorBMWfB2WVpFjQtfk0FRo4yqUFjGth70r5nGnG0X7R1pSNdgl86yX1olKCFynssBIXqNnKuhjsevYSjC+G18Pgx2hwc9XY2SGn5AP5SAJySW7Id3JHxoSTP07POXFO3cCduLE7fS51nabnmGyFO/8L1OHLhA==</latexit> <latexit sha1_base64="KksKdRyhI0qOgtDRpYhf7ThpXdA=">AAACrnicbVHRatswFJXdrUvdrUvSt/ZFLBT20mB32doyBoW+7LGDZSnYJsjydSIqy0a6Hgkmj/3IfsN+YkpqmJPugsTRufeeKx0lpRQGff/Jcfdevd5/0znwDt++O3rf7fV/maLSHMa8kIW+T5gBKRSMUaCE+1IDyxMJk+Thdp2f/AZtRKF+4rKEOGczJTLBGVpq2n1c0Ogr/bbevEhChjSkUQIzoWqmNVuuar3yzi9pFIXDEeSxR0f/8PmnFv+lhT/T1sFvHwIvApU22l6kxWyONJ52B/7Q3wR9CYIGDEgTd9Oe04/Sglc5KOSSGRMGfomx1UXBJVjlykDJ+AObQWihYjmYuN74taJnlklpVmi7FNIN2+6oWW7MMk9sZc5wbnZza/J/ubDC7CquhSorBMWfB2WVpFjQtfk0FRo4yqUFjGth70r5nGnG0X7R1pSNdgl86yX1olKCFynssBIXqNnKuhjsevYSjC+G18Pgx2hwc9XY2SGn5AP5SAJySW7Id3JHxoSTP07POXFO3cCduLE7fS51nabnmGyFO/8L1OHLhA==</latexit> <latexit sha1_base64="KksKdRyhI0qOgtDRpYhf7ThpXdA=">AAACrnicbVHRatswFJXdrUvdrUvSt/ZFLBT20mB32doyBoW+7LGDZSnYJsjydSIqy0a6Hgkmj/3IfsN+YkpqmJPugsTRufeeKx0lpRQGff/Jcfdevd5/0znwDt++O3rf7fV/maLSHMa8kIW+T5gBKRSMUaCE+1IDyxMJk+Thdp2f/AZtRKF+4rKEOGczJTLBGVpq2n1c0Ogr/bbevEhChjSkUQIzoWqmNVuuar3yzi9pFIXDEeSxR0f/8PmnFv+lhT/T1sFvHwIvApU22l6kxWyONJ52B/7Q3wR9CYIGDEgTd9Oe04/Sglc5KOSSGRMGfomx1UXBJVjlykDJ+AObQWihYjmYuN74taJnlklpVmi7FNIN2+6oWW7MMk9sZc5wbnZza/J/ubDC7CquhSorBMWfB2WVpFjQtfk0FRo4yqUFjGth70r5nGnG0X7R1pSNdgl86yX1olKCFynssBIXqNnKuhjsevYSjC+G18Pgx2hwc9XY2SGn5AP5SAJySW7Id3JHxoSTP07POXFO3cCduLE7fS51nabnmGyFO/8L1OHLhA==</latexit> 0 − 5 − 2 xi = Sij Sij <latexit sha1_base64="6Iv2z52WvxSnJvX12CP4j21Z+nA=">AAACQHicbVDLSgMxFM34rPXV1oULN8EiurHMiKAuhIIblxWtFWoZMultjWYyQ3JHWob5Grf6FX6Fn+BK3LoyfSxs64HA4Zz7yD1BLIVB1/1w5uYXFpeWcyv51bX1jc1CsXRrokRzqPNIRvouYAakUFBHgRLuYg0sDCQ0gqeLgd94Bm1EpG6wH0MrZF0lOoIztJJf2O75gp7Taz8Vj/sZPRyxLO8Xym7FHYLOEm9MymSMml90SvftiCchKOSSGdP03BhbKdMouIQsf58YiBl/Yl1oWqpYCKaVDi/I6J5V2rQTafsU0qH6tyNloTH9MLCVIcMHM+0NxP+8ZoKd01YqVJwgKD5a1EkkxYgO4qBtoYGj7FvCuBb2r5Q/MM042tAmtgxnx8AnLkl7iRI8asOUKrGHmmU2RW86s1lSP6qcVbyr43L1dBxnjuyQXXJAPHJCquSS1EidcJKRF/JK3px359P5cr5HpXPOuGeLTMD5+QWvkq9d</latexit> <latexit sha1_base64="6Iv2z52WvxSnJvX12CP4j21Z+nA=">AAACQHicbVDLSgMxFM34rPXV1oULN8EiurHMiKAuhIIblxWtFWoZMultjWYyQ3JHWob5Grf6FX6Fn+BK3LoyfSxs64HA4Zz7yD1BLIVB1/1w5uYXFpeWcyv51bX1jc1CsXRrokRzqPNIRvouYAakUFBHgRLuYg0sDCQ0gqeLgd94Bm1EpG6wH0MrZF0lOoIztJJf2O75gp7Taz8Vj/sZPRyxLO8Xym7FHYLOEm9MymSMml90SvftiCchKOSSGdP03BhbKdMouIQsf58YiBl/Yl1oWqpYCKaVDi/I6J5V2rQTafsU0qH6tyNloTH9MLCVIcMHM+0NxP+8ZoKd01YqVJwgKD5a1EkkxYgO4qBtoYGj7FvCuBb2r5Q/MM042tAmtgxnx8AnLkl7iRI8asOUKrGHmmU2RW86s1lSP6qcVbyr43L1dBxnjuyQXXJAPHJCquSS1EidcJKRF/JK3px359P5cr5HpXPOuGeLTMD5+QWvkq9d</latexit> <latexit sha1_base64="6Iv2z52WvxSnJvX12CP4j21Z+nA=">AAACQHicbVDLSgMxFM34rPXV1oULN8EiurHMiKAuhIIblxWtFWoZMultjWYyQ3JHWob5Grf6FX6Fn+BK3LoyfSxs64HA4Zz7yD1BLIVB1/1w5uYXFpeWcyv51bX1jc1CsXRrokRzqPNIRvouYAakUFBHgRLuYg0sDCQ0gqeLgd94Bm1EpG6wH0MrZF0lOoIztJJf2O75gp7Taz8Vj/sZPRyxLO8Xym7FHYLOEm9MymSMml90SvftiCchKOSSGdP03BhbKdMouIQsf58YiBl/Yl1oWqpYCKaVDi/I6J5V2rQTafsU0qH6tyNloTH9MLCVIcMHM+0NxP+8ZoKd01YqVJwgKD5a1EkkxYgO4qBtoYGj7FvCuBb2r5Q/MM042tAmtgxnx8AnLkl7iRI8asOUKrGHmmU2RW86s1lSP6qcVbyr43L1dBxnjuyQXXJAPHJCquSS1EidcJKRF/JK3px359P5cr5HpXPOuGeLTMD5+QWvkq9d</latexit> <latexit sha1_base64="6Iv2z52WvxSnJvX12CP4j21Z+nA=">AAACQHicbVDLSgMxFM34rPXV1oULN8EiurHMiKAuhIIblxWtFWoZMultjWYyQ3JHWob5Grf6FX6Fn+BK3LoyfSxs64HA4Zz7yD1BLIVB1/1w5uYXFpeWcyv51bX1jc1CsXRrokRzqPNIRvouYAakUFBHgRLuYg0sDCQ0gqeLgd94Bm1EpG6wH0MrZF0lOoIztJJf2O75gp7Taz8Vj/sZPRyxLO8Xym7FHYLOEm9MymSMml90SvftiCchKOSSGdP03BhbKdMouIQsf58YiBl/Yl1oWqpYCKaVDi/I6J5V2rQTafsU0qH6tyNloTH9MLCVIcMHM+0NxP+8ZoKd01YqVJwgKD5a1EkkxYgO4qBtoYGj7FvCuBb2r5Q/MM042tAmtgxnx8AnLkl7iRI8asOUKrGHmmU2RW86s1lSP6qcVbyr43L1dBxnjuyQXXJAPHJCquSS1EidcJKRF/JK3px359P5cr5HpXPOuGeLTMD5+QWvkq9d</latexit>
- 24. 6. DYNAMIC PROGRAMMING I ‣ weighted interval scheduling ‣ segmented least squares ‣ knapsack problem ‣ RNA secondary structure SECTION 6.3
- 25. Least squares Least squares. Foundational problem in statistics. ・Given n points in the plane: (x1, y1), (x2, y2) , …, (xn, yn). ・Find a line y = ax + b that minimizes the sum of the squared error: Solution. Calculus ⇒ min error is achieved when x y 25 a = n ! i xiyi − ( ! i xi)( ! i yi) n ! i x2 i − ( ! i xi)2 , b = ! i yi − a ! i xi n <latexit sha1_base64="h5fKMH7NWGnBcmDeMLEiuZrLM70=">AAACunicbVFNb9QwEHXCVylf23JESBYV0EqwSvbSIlSpEheORWJppc02mjiT1lrHCfYY7SrKj+BncOTncONfcMXZLWo3ZSTbT2/ezNjPWa2kpSj6FYS3bt+5e2/j/uaDh48ePxlsbX+xlTMCx6JSlTnNwKKSGsckSeFpbRDKTOFJNvvQ5U++obGy0p9pUeO0hHMtCymAPJUOvgNP3vPDbksKA6LRPLGuTCWfp3Lhj7d894rY+4d9Zq9d056NetKzUfuGJ18d5Dzrzbhq4mvgWhPfsk0HO9EwWga/CeJLsHO0/+Pnb8bYcboVbCd5JVyJmoQCaydxVNO0AUNSKGw3E2exBjGDc5x4qKFEO22W3rX8pWdyXlTGL018yV6vaKC0dlFmXlkCXdh+riP/l5s4Kg6mjdS1I9RiNahwilPFu4/guTQoSC08AGGkvysXF+DtIf9da1OWvWsUay9p5k5LUeXYYxXNyUDnYtz37CYYj4bvhvEn7+YBW8UGe8ZesF0Ws312xD6yYzZmgv0JngevgtfhYShCGc5W0jC4rHnK1iKkv7SR1/Q=</latexit> <latexit sha1_base64="osgmybCFlDRwfvDA5+Vdeo/74To=">AAACunicbVHBTtwwEHXSllJaYKHHqpJV1BYErJK9AKqQkHrhSKVuQdos0cRxwFrHSe1xtaso4hv4DI79HI79il5xdqlgQ0ey/fTmzYz9nJRSGAyCW89/9vzFwsvFV0uv3yyvrHbW1n+YwmrG+6yQhT5LwHApFO+jQMnPSs0hTyQ/TUZfm/zpL66NKNR3nJR8mMOFEplggI6KO9dAoy/0sNmiTAOrFI2MzWNBx7GYuGOXbj4QW/+wy2zVc9rzXkt63qt3aPTTQkqT1oyHJq4GHjVxLeu4sxF0g2nQpyC8BxtHeze/b7ev/pzEa956lBbM5lwhk2DMIAxKHFagUTDJ66XIGl4CG8EFHzioIOdmWE29q+lHx6Q0K7RbCumUfVxRQW7MJE+cMge8NO1cQ/4vN7CY7Q8roUqLXLHZoMxKigVtPoKmQnOGcuIAMC3cXSm7BGcPuu+amzLtXXI295JqbJVgRcpbrMQxamhcDNuePQX9XvegG35zbu6TWSySd+QD2SQh2SNH5JickD5h5K/33vvkffYPfeYLfzST+t59zVsyFz7eARtS2Xg=</latexit> <latexit sha1_base64="osgmybCFlDRwfvDA5+Vdeo/74To=">AAACunicbVHBTtwwEHXSllJaYKHHqpJV1BYErJK9AKqQkHrhSKVuQdos0cRxwFrHSe1xtaso4hv4DI79HI79il5xdqlgQ0ey/fTmzYz9nJRSGAyCW89/9vzFwsvFV0uv3yyvrHbW1n+YwmrG+6yQhT5LwHApFO+jQMnPSs0hTyQ/TUZfm/zpL66NKNR3nJR8mMOFEplggI6KO9dAoy/0sNmiTAOrFI2MzWNBx7GYuGOXbj4QW/+wy2zVc9rzXkt63qt3aPTTQkqT1oyHJq4GHjVxLeu4sxF0g2nQpyC8BxtHeze/b7ev/pzEa956lBbM5lwhk2DMIAxKHFagUTDJ66XIGl4CG8EFHzioIOdmWE29q+lHx6Q0K7RbCumUfVxRQW7MJE+cMge8NO1cQ/4vN7CY7Q8roUqLXLHZoMxKigVtPoKmQnOGcuIAMC3cXSm7BGcPuu+amzLtXXI295JqbJVgRcpbrMQxamhcDNuePQX9XvegG35zbu6TWSySd+QD2SQh2SNH5JickD5h5K/33vvkffYPfeYLfzST+t59zVsyFz7eARtS2Xg=</latexit> <latexit sha1_base64="uSR6MIDaEDPJwkbPgs/ygO2X/DQ=">AAACunicbVHbatwwEJXdW5reNuljKYgubRNoF3tfklICgb70MYVuE1hvzFgeJ2Jl2ZVGYRfjj+jn9Uv6WnmzJVmnA5IOZ87MSEdZraSlKPodhPfuP3j4aOvx9pOnz56/GOzs/rCVMwInolKVOcvAopIaJyRJ4VltEMpM4Wk2/9LlT6/QWFnp77SscVbChZaFFECeSge/gCef+VG3JYUB0WieWFemki9SufTHR753Q+z/wz6z325oz8c96fm4/cCTnw5ynvVm3DTxNXCriW/ZpoNhNIpWwe+CeA2GbB0n6U6wm+SVcCVqEgqsncZRTbMGDEmhsN1OnMUaxBwucOqhhhLtrFl51/K3nsl5URm/NPEVe7uigdLaZZl5ZQl0afu5jvxfbuqoOJw1UteOUIvrQYVTnCrefQTPpUFBaukBCCP9Xbm4BG8P+e/amLLqXaPYeEmzcFqKKsceq2hBBjoX475nd8FkPPo0ir9Fw+PDtZ1b7BV7w/ZYzA7YMfvKTtiECfYneB28C96HR6EIZTi/lobBuuYl24iQ/gJmldVD</latexit> SSE = n ! i=1 (yi − axi − b)2 <latexit sha1_base64="Pz37uMf9ZkSqUadkulfgYpEBW/M=">AAACV3icbVBNTxsxEJ0slAb6laRHLhaoUnpotMulVFWqSAipxyAIRErCyutMEguvd2XPtolW+Rf8FySu7Z9ofw3eDQcSeJLt5zczHs+LUiUt+f6/ire1/WrndXV3783bd+8/1OqNS5tkRmBPJCox/YhbVFJjjyQp7KcGeRwpvIpuTor41S80Vib6ghYpjmI+1XIiBScnhbXW+fkpG35n7WIb2iwOc9kOlte6uDcXoWRfGJ+XR/T5+iisHfotvwR7ToJHctj5cfcbHLphvdIYjhORxahJKG7tIPBTGuXckBQKl3vDzGLKxQ2f4sBRzWO0o7wcbMk+OWXMJolxSxMr1acVOY+tXcSRy4w5zexmrBBfig0ymhyPcqnTjFCLVaNJphglrHCJjaVBQWrhCBdGur8yMeOGC3JernUp305RrE2SzzMtRTLGDVXRnAxfOheDTc+ek95R61srOHNuHsMKVdiHA2hCAF+hAz+hCz0QcAv38Af+Vv574O141VWqV3ms+Qhr8OoPzEWz8Q==</latexit> <latexit sha1_base64="kNKMdq3i/R2HN6/wEHFPEtvhKsQ=">AAACV3icbVDNThsxEJ4sLQT6l4QjF6uoEj002uVSEAJFQkgcqSBAlYSV15mAhde7smch0SpvwZnXQOIKLwGv0RfAu+FAQkey/fn7ZjyeL0qVtOT7TxVv7sPH+YXq4tKnz1++fqvVG8c2yYzAtkhUYk4jblFJjW2SpPA0NcjjSOFJdLlb6CdXaKxM9BGNUuzF/FzLgRScHBXWmoeHe6y7xbaLrWuzOMzldjA+08V9bRRK9ovxYXlEP8/Ww9qq3/TLYO9B8ApWWzt31wu3f/8dhPVKo9tPRBajJqG4tZ3AT6mXc0NSKBwvdTOLKReX/Bw7Dmoeo+3l5WBj9sMxfTZIjFuaWMm+rch5bO0ojlxmzOnCzmoF+T+tk9Fgo5dLnWaEWkwaDTLFKGGFS6wvDQpSIwe4MNL9lYkLbrgg5+VUl/LtFMXUJPkw01IkfZxhFQ3J8LFzMZj17D1orzc3m8Ef5+YGTKIKK/Ad1iCA39CCfTiANgi4gXt4gMfKswfevFedpHqV15plmAqv/gLgYbXi</latexit> <latexit sha1_base64="kNKMdq3i/R2HN6/wEHFPEtvhKsQ=">AAACV3icbVDNThsxEJ4sLQT6l4QjF6uoEj002uVSEAJFQkgcqSBAlYSV15mAhde7smch0SpvwZnXQOIKLwGv0RfAu+FAQkey/fn7ZjyeL0qVtOT7TxVv7sPH+YXq4tKnz1++fqvVG8c2yYzAtkhUYk4jblFJjW2SpPA0NcjjSOFJdLlb6CdXaKxM9BGNUuzF/FzLgRScHBXWmoeHe6y7xbaLrWuzOMzldjA+08V9bRRK9ovxYXlEP8/Ww9qq3/TLYO9B8ApWWzt31wu3f/8dhPVKo9tPRBajJqG4tZ3AT6mXc0NSKBwvdTOLKReX/Bw7Dmoeo+3l5WBj9sMxfTZIjFuaWMm+rch5bO0ojlxmzOnCzmoF+T+tk9Fgo5dLnWaEWkwaDTLFKGGFS6wvDQpSIwe4MNL9lYkLbrgg5+VUl/LtFMXUJPkw01IkfZxhFQ3J8LFzMZj17D1orzc3m8Ef5+YGTKIKK/Ad1iCA39CCfTiANgi4gXt4gMfKswfevFedpHqV15plmAqv/gLgYbXi</latexit> <latexit sha1_base64="Zy1LiC11wpnyrhTk6pqMmahVKW8=">AAACV3icbVBNb9NAEJ0YaEP5SsKRy4oIKRyw7F5aVFWqhJA4BpXQSPmw1ptJsup6be2Oq0SW/0V/DVf4E/BrWLs+kISRdvftezM7Oy/OlLQUBL9b3qPHT46O209Pnj1/8fJVp9v7btPcCByJVKVmHHOLSmockSSF48wgT2KFN/Htp0q/uUNjZaq/0TbDWcJXWi6l4OSoqONfX39m0wt2WW1TmydRIS/Dcq6r+2AbSfaB8U19xO/np1GnH/hBHewQhA3oQxPDqNvqTRepyBPUJBS3dhIGGc0KbkgKheXJNLeYcXHLVzhxUPME7ayoByvZO8cs2DI1bmliNftvRcETa7dJ7DITTmu7r1Xk/7RJTsvzWSF1lhNq8dBomStGKatcYgtpUJDaOsCFke6vTKy54YKclztd6rczFDuTFJtcS5EucI9VtCHDS+diuO/ZIRid+h/98GvQvzpv7GzDG3gLAwjhDK7gCwxhBALu4Qf8hF+tPx54R177IdVrNTWvYSe87l8eaLJF</latexit>
- 26. Segmented least squares Segmented least squares. ・Points lie roughly on a sequence of several line segments. ・Given n points in the plane: (x1, y1), (x2, y2) , …, (xn, yn) with x1 < x2 < ... < xn, find a sequence of lines that minimizes f (x). Q. What is a reasonable choice for f (x) to balance accuracy and parsimony? x y 26 goodness of fit number of lines
- 27. Segmented least squares Segmented least squares. ・Points lie roughly on a sequence of several line segments. ・Given n points in the plane: (x1, y1), (x2, y2) , …, (xn, yn) with x1 < x2 < ... < xn, find a sequence of lines that minimizes f (x). Goal. Minimize f (x) = E + c L for some constant c > 0, where ・E = sum of the sums of the squared errors in each segment. ・L = number of lines. x y 27
- 28. Dynamic programming: multiway choice Notation. ・OPT(j) = minimum cost for points p1, p2, …, pj. ・eij = SSE for for points pi, pi+1, …, pj. To compute OPT(j): ・Last segment uses points pi, pi+1, …, pj for some i ≤ j. ・Cost = eij + c + OPT(i – 1). Bellman equation. 28 optimal substructure property (proof via exchange argument) OPT(j) = 0 B7 j = 0 min 1 i j { eij + c + OPT(i 1) } B7 j > 0 <latexit sha1_base64="3Vqhon9XuZlMDxUy0KO6LsmTpKw=">AAAC6XicbVFNaxsxENVuv1L3I0567GWoaUgoNbtpoQkmJdBLD4W6ECcByxitPGvL0WoXSRtsxP6Jnkqv/SP9G/031W58qO0OSHq8edKbGSWFFMZG0Z8gvHf/wcNHO49bT54+e77b3tu/NHmpOQ54LnN9nTCDUigcWGElXhcaWZZIvEpuPtX5q1vURuTqwi4LHGVsqkQqOLOeGrd/f+1fHM6PgPbOaK9FE5wK5bh/0FQt2ovgAKjFhQUHIoUK5nAGEVA67L7DbOQVNBOKSpEJa8aOmjIxlvEbVyuOvQJioBJBNPu8quoztUCdNwQcOzGv4A1wv+o6xNv4yPNUi+nMi6pt94+Ne4uimqyqHLc7UTdqArZBvAIdsor+eC/Yp5OclxkqyyUzZhhHhR05pq3gEn3bpcHCN8GmOPRQsQzNyDWjruC1ZyaQ5tovZaFh/73hWGbMMku8MmN2ZjZzNfm/3LC06cnICVWUFhW/M0pLCTaH+t9gIjRyK5ceMK6FrxX4jGnGrf/dNZfm7QL5WiduUSrB8wlusNIurGb1FOPNmW2DwXH3tBt/e985P1mNc4e8JK/IIYnJB3JOPpM+GRAeHARfgkFwGcrwe/gj/HknDYPVnRdkLcJffwFz2eL9</latexit> <latexit sha1_base64="3Vqhon9XuZlMDxUy0KO6LsmTpKw=">AAAC6XicbVFNaxsxENVuv1L3I0567GWoaUgoNbtpoQkmJdBLD4W6ECcByxitPGvL0WoXSRtsxP6Jnkqv/SP9G/031W58qO0OSHq8edKbGSWFFMZG0Z8gvHf/wcNHO49bT54+e77b3tu/NHmpOQ54LnN9nTCDUigcWGElXhcaWZZIvEpuPtX5q1vURuTqwi4LHGVsqkQqOLOeGrd/f+1fHM6PgPbOaK9FE5wK5bh/0FQt2ovgAKjFhQUHIoUK5nAGEVA67L7DbOQVNBOKSpEJa8aOmjIxlvEbVyuOvQJioBJBNPu8quoztUCdNwQcOzGv4A1wv+o6xNv4yPNUi+nMi6pt94+Ne4uimqyqHLc7UTdqArZBvAIdsor+eC/Yp5OclxkqyyUzZhhHhR05pq3gEn3bpcHCN8GmOPRQsQzNyDWjruC1ZyaQ5tovZaFh/73hWGbMMku8MmN2ZjZzNfm/3LC06cnICVWUFhW/M0pLCTaH+t9gIjRyK5ceMK6FrxX4jGnGrf/dNZfm7QL5WiduUSrB8wlusNIurGb1FOPNmW2DwXH3tBt/e985P1mNc4e8JK/IIYnJB3JOPpM+GRAeHARfgkFwGcrwe/gj/HknDYPVnRdkLcJffwFz2eL9</latexit> <latexit sha1_base64="3Vqhon9XuZlMDxUy0KO6LsmTpKw=">AAAC6XicbVFNaxsxENVuv1L3I0567GWoaUgoNbtpoQkmJdBLD4W6ECcByxitPGvL0WoXSRtsxP6Jnkqv/SP9G/031W58qO0OSHq8edKbGSWFFMZG0Z8gvHf/wcNHO49bT54+e77b3tu/NHmpOQ54LnN9nTCDUigcWGElXhcaWZZIvEpuPtX5q1vURuTqwi4LHGVsqkQqOLOeGrd/f+1fHM6PgPbOaK9FE5wK5bh/0FQt2ovgAKjFhQUHIoUK5nAGEVA67L7DbOQVNBOKSpEJa8aOmjIxlvEbVyuOvQJioBJBNPu8quoztUCdNwQcOzGv4A1wv+o6xNv4yPNUi+nMi6pt94+Ne4uimqyqHLc7UTdqArZBvAIdsor+eC/Yp5OclxkqyyUzZhhHhR05pq3gEn3bpcHCN8GmOPRQsQzNyDWjruC1ZyaQ5tovZaFh/73hWGbMMku8MmN2ZjZzNfm/3LC06cnICVWUFhW/M0pLCTaH+t9gIjRyK5ceMK6FrxX4jGnGrf/dNZfm7QL5WiduUSrB8wlusNIurGb1FOPNmW2DwXH3tBt/e985P1mNc4e8JK/IIYnJB3JOPpM+GRAeHARfgkFwGcrwe/gj/HknDYPVnRdkLcJffwFz2eL9</latexit> <latexit sha1_base64="3Vqhon9XuZlMDxUy0KO6LsmTpKw=">AAAC6XicbVFNaxsxENVuv1L3I0567GWoaUgoNbtpoQkmJdBLD4W6ECcByxitPGvL0WoXSRtsxP6Jnkqv/SP9G/031W58qO0OSHq8edKbGSWFFMZG0Z8gvHf/wcNHO49bT54+e77b3tu/NHmpOQ54LnN9nTCDUigcWGElXhcaWZZIvEpuPtX5q1vURuTqwi4LHGVsqkQqOLOeGrd/f+1fHM6PgPbOaK9FE5wK5bh/0FQt2ovgAKjFhQUHIoUK5nAGEVA67L7DbOQVNBOKSpEJa8aOmjIxlvEbVyuOvQJioBJBNPu8quoztUCdNwQcOzGv4A1wv+o6xNv4yPNUi+nMi6pt94+Ne4uimqyqHLc7UTdqArZBvAIdsor+eC/Yp5OclxkqyyUzZhhHhR05pq3gEn3bpcHCN8GmOPRQsQzNyDWjruC1ZyaQ5tovZaFh/73hWGbMMku8MmN2ZjZzNfm/3LC06cnICVWUFhW/M0pLCTaH+t9gIjRyK5ceMK6FrxX4jGnGrf/dNZfm7QL5WiduUSrB8wlusNIurGb1FOPNmW2DwXH3tBt/e985P1mNc4e8JK/IIYnJB3JOPpM+GRAeHARfgkFwGcrwe/gj/HknDYPVnRdkLcJffwFz2eL9</latexit>
- 29. Segmented least squares algorithm 29 SEGMENTED-LEAST-SQUARES(n, p1, …, pn, c) __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ FOR j = 1 TO n FOR i = 1 TO j Compute the SSE eij for the points pi, pi+1, …, pj. M[0] ← 0. FOR j = 1 TO n M[j] ← min 1 ≤ i ≤ j { eij + c + M[i – 1] }. RETURN M[n]. __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ previously computed value
- 30. Segmented least squares analysis Theorem. [Bellman 1961] DP algorithm solves the segmented least squares problem in O(n3 ) time and O(n2 ) space. Pf. ・Bottleneck = computing SSE eij for each i and j. ・O(n) to compute eij. ▪ Remark. Can be improved to O(n2 ) time. ・For each i : precompute cumulative sums . ・Using cumulative sums, can compute eij in O(1) time. 30 aij = n ! k xkyk − ( ! k xk)( ! k yk) n ! k x2 k − ( ! k xk)2 , bij = ! k yk − aij ! k xk n <latexit sha1_base64="JiXEyfCjefrho5PdKjL7JUVzDmM=">AAACyXicbVHdStxAFJ6krf/a1V72ZqgUFOySLLQqpbDgTS96YaFbhc0aTiYnOt3JJM6P7Dbkqi/iO/g0gg/Tya7W7uqBmfn4zu98JykF1yYIbj3/xctXC4tLyyura+sbr1ubWz91YRXDHitEoU4T0Ci4xJ7hRuBpqRDyROBJMjxq/CdXqDQv5A8zLnGQw7nkGWdgHBW3riGu+K+aRp/pl+aKMgWskjTSNo+HdBQPx+75QHceid0H7Dy79UzsWWcu9KxT79Ho0kJKk+caPVZyiQ+j/Et3xeu4tR20g4nRpyC8B9vd/Zu7LiHkON70tqK0YDZHaZgArfthUJpBBcpwJrBeiazGEtgQzrHvoIQc9aCaSFnT945JaVYod6ShE/b/jApyrcd54iJzMBd63teQz/n61mQHg4rL0hqUbNoos4KagjZ7oSlXyIwYOwBMcTcrZRfgNDJuezNdJrVLZDM/qUZWclakOMcKMzIKGhXDec2egl6nfdgOvzs1D8jUlshb8o7skJDsky75So5JjzBvwdvzPnqf/G++8kf+72mo793nvCEz5v/5CzSm3bw=</latexit> <latexit sha1_base64="CRJSkf/k/PXSE8sZbaW7avsGjhU=">AAACyXicbVHdTtRAFJ5WBQTUBS69mUhMIMFNu4ksRk1IvOHCC0xcIdkuzen0FIadTuv8mF2bXvEiJj6CT0PgYZzugrgLJ5mZL9/5ne8kpeDaBMGl5z96/GRhcenp8srqs+cvWmvr33RhFcMeK0ShjhPQKLjEnuFG4HGpEPJE4FEy/NT4j36g0ryQX824xEEOp5JnnIFxVNz6BXHFz2savacfmyvKFLBK0kjbPB7SUTwcu+cN3bojtm+x82zXM7EnnbnQk069Q6PvFlKaPNTorpJLvB3lX7orXsetzaAdTIzeB+EN2Nzv/rnu/r76cBiveetRWjCbozRMgNb9MCjNoAJlOBNYL0dWYwlsCKfYd1BCjnpQTaSs6WvHpDQrlDvS0An7f0YFudbjPHGROZgzPe9ryId8fWuyvUHFZWkNSjZtlFlBTUGbvdCUK2RGjB0ApriblbIzcBoZt72ZLpPaJbKZn1QjKzkrUpxjhRkZBY2K4bxm90Gv037XDr84NffI1JbIS/KKbJGQdMk+OSCHpEeYt+DteG+9Xf+zr/yR/3Ma6ns3ORtkxvyLv+PP320=</latexit> <latexit sha1_base64="CRJSkf/k/PXSE8sZbaW7avsGjhU=">AAACyXicbVHdTtRAFJ5WBQTUBS69mUhMIMFNu4ksRk1IvOHCC0xcIdkuzen0FIadTuv8mF2bXvEiJj6CT0PgYZzugrgLJ5mZL9/5ne8kpeDaBMGl5z96/GRhcenp8srqs+cvWmvr33RhFcMeK0ShjhPQKLjEnuFG4HGpEPJE4FEy/NT4j36g0ryQX824xEEOp5JnnIFxVNz6BXHFz2savacfmyvKFLBK0kjbPB7SUTwcu+cN3bojtm+x82zXM7EnnbnQk069Q6PvFlKaPNTorpJLvB3lX7orXsetzaAdTIzeB+EN2Nzv/rnu/r76cBiveetRWjCbozRMgNb9MCjNoAJlOBNYL0dWYwlsCKfYd1BCjnpQTaSs6WvHpDQrlDvS0An7f0YFudbjPHGROZgzPe9ryId8fWuyvUHFZWkNSjZtlFlBTUGbvdCUK2RGjB0ApriblbIzcBoZt72ZLpPaJbKZn1QjKzkrUpxjhRkZBY2K4bxm90Gv037XDr84NffI1JbIS/KKbJGQdMk+OSCHpEeYt+DteG+9Xf+zr/yR/3Ma6ns3ORtkxvyLv+PP320=</latexit> <latexit sha1_base64="BChx1F3fNhGq6mUCFDX2bORLMoA=">AAACyXicbVFdb9MwFHUCjDG+uvHIi0WFtEmjSioBQwhpEi888DAkyiY1XXTj3GxeHSfY16glyhN/hL/Fv8HpOka7Xcn20bmfPjerlbQURX+C8M7dexv3Nx9sPXz0+MnT3vbON1s5I3AkKlWZkwwsKqlxRJIUntQGocwUHmfTj53/+AcaKyv9leY1Tko407KQAshTae83pI28aHnynn/orqQwIBrNE+vKdMpn6XTun1d895rYu8Les9euxJ4O10JPh+0+T747yHl2W6PrSj7xapR/6b54m/b60SBaGL8J4iXos6UdpdvBTpJXwpWoSSiwdhxHNU0aMCSFwnYrcRZrEFM4w7GHGkq0k2YhZctfeibnRWX80cQX7P8ZDZTWzsvMR5ZA53bd15G3+caOioNJI3XtCLW4bFQ4xani3V54Lg0KUnMPQBjpZ+XiHLxG5Le30mVRu0ax8pNm5rQUVY5rrKIZGehUjNc1uwlGw8G7Qfwl6h8eLOXcZM/ZC7bLYvaWHbJP7IiNmAg2gv3gdfAm/ByacBb+vAwNg2XOM7Zi4a+/kPPbdg==</latexit> i k=1 xk, i k=1 yk, i k=1 x2 k, i k=1 xkyk <latexit sha1_base64="E9Bo6rLIFL0/cuHYqsa/2SHtfn0=">AAACh3icbVDLSgMxFE3Hd33VunQTLIILKTMiPhZCxY1LBatCH0Mmc6uhmcyY3EjL0L/zJ/wFt/oBpnUQWz0QOJxzT25yokwKg77/VvLm5hcWl5ZXyqtr6xubla3qnUmt5tDkqUz1Q8QMSKGgiQIlPGQaWBJJuI/6l2P//gW0Eam6xWEGnYQ9KtETnKGTwkq3bWwS5v3zYNQVdBD2D2j72bKYTunDH708O989/DfhnHEqrNT8uj8B/UuCgtRIgetwq1Rtxym3CSjkkhnTCvwMOznTKLiEUbltDWSM99kjtBxVLAHTySdFjOieU2LaS7U7CulE/Z3IWWLMMIncZMLwycx6Y/E/r2Wxd9rJhcosguLfi3pWUkzpuFUaCw0c5dARxrVwb6X8iWnG0XU/tWVydwZ86if5wCrB0xhmVIkD1GzkWgxmO/tLmof1s3pwc1RrnBZ1LpMdskv2SUBOSINckWvSJJy8knfyQT69sud7x14x65WKzDaZgnfxBVkmxzI=</latexit> <latexit sha1_base64="E9Bo6rLIFL0/cuHYqsa/2SHtfn0=">AAACh3icbVDLSgMxFE3Hd33VunQTLIILKTMiPhZCxY1LBatCH0Mmc6uhmcyY3EjL0L/zJ/wFt/oBpnUQWz0QOJxzT25yokwKg77/VvLm5hcWl5ZXyqtr6xubla3qnUmt5tDkqUz1Q8QMSKGgiQIlPGQaWBJJuI/6l2P//gW0Eam6xWEGnYQ9KtETnKGTwkq3bWwS5v3zYNQVdBD2D2j72bKYTunDH708O989/DfhnHEqrNT8uj8B/UuCgtRIgetwq1Rtxym3CSjkkhnTCvwMOznTKLiEUbltDWSM99kjtBxVLAHTySdFjOieU2LaS7U7CulE/Z3IWWLMMIncZMLwycx6Y/E/r2Wxd9rJhcosguLfi3pWUkzpuFUaCw0c5dARxrVwb6X8iWnG0XU/tWVydwZ86if5wCrB0xhmVIkD1GzkWgxmO/tLmof1s3pwc1RrnBZ1LpMdskv2SUBOSINckWvSJJy8knfyQT69sud7x14x65WKzDaZgnfxBVkmxzI=</latexit> <latexit sha1_base64="E9Bo6rLIFL0/cuHYqsa/2SHtfn0=">AAACh3icbVDLSgMxFE3Hd33VunQTLIILKTMiPhZCxY1LBatCH0Mmc6uhmcyY3EjL0L/zJ/wFt/oBpnUQWz0QOJxzT25yokwKg77/VvLm5hcWl5ZXyqtr6xubla3qnUmt5tDkqUz1Q8QMSKGgiQIlPGQaWBJJuI/6l2P//gW0Eam6xWEGnYQ9KtETnKGTwkq3bWwS5v3zYNQVdBD2D2j72bKYTunDH708O989/DfhnHEqrNT8uj8B/UuCgtRIgetwq1Rtxym3CSjkkhnTCvwMOznTKLiEUbltDWSM99kjtBxVLAHTySdFjOieU2LaS7U7CulE/Z3IWWLMMIncZMLwycx6Y/E/r2Wxd9rJhcosguLfi3pWUkzpuFUaCw0c5dARxrVwb6X8iWnG0XU/tWVydwZ86if5wCrB0xhmVIkD1GzkWgxmO/tLmof1s3pwc1RrnBZ1LpMdskv2SUBOSINckWvSJJy8knfyQT69sud7x14x65WKzDaZgnfxBVkmxzI=</latexit> <latexit sha1_base64="E9Bo6rLIFL0/cuHYqsa/2SHtfn0=">AAACh3icbVDLSgMxFE3Hd33VunQTLIILKTMiPhZCxY1LBatCH0Mmc6uhmcyY3EjL0L/zJ/wFt/oBpnUQWz0QOJxzT25yokwKg77/VvLm5hcWl5ZXyqtr6xubla3qnUmt5tDkqUz1Q8QMSKGgiQIlPGQaWBJJuI/6l2P//gW0Eam6xWEGnYQ9KtETnKGTwkq3bWwS5v3zYNQVdBD2D2j72bKYTunDH708O989/DfhnHEqrNT8uj8B/UuCgtRIgetwq1Rtxym3CSjkkhnTCvwMOznTKLiEUbltDWSM99kjtBxVLAHTySdFjOieU2LaS7U7CulE/Z3IWWLMMIncZMLwycx6Y/E/r2Wxd9rJhcosguLfi3pWUkzpuFUaCw0c5dARxrVwb6X8iWnG0XU/tWVydwZ86if5wCrB0xhmVIkD1GzkWgxmO/tLmof1s3pwc1RrnBZ1LpMdskv2SUBOSINckWvSJJy8knfyQT69sud7x14x65WKzDaZgnfxBVkmxzI=</latexit>
- 31. 6. DYNAMIC PROGRAMMING I ‣ weighted interval scheduling ‣ segmented least squares ‣ knapsack problem ‣ RNA secondary structure SECTION 6.4
- 32. Knapsack problem Goal. Pack knapsack so as to maximize total value of items taken. ・There are n items: item i provides value vi > 0 and weighs wi > 0. ・Value of a subset of items = sum of values of individual items. ・Knapsack has weight limit of W. Ex. The subset { 1, 2, 5 } has value $35 (and weight 10). Ex. The subset { 3, 4 } has value $40 (and weight 11). Assumption. All values and weights are integral. 32 weights and values can be arbitrary positive integers $28 7 kg $22 6 kg $6 2 kg $1 1 kg $18 5 kg 11 kg Creative Commons Attribution-Share Alike 2.5 by Dake i vi wi 1 $1 1 kg 2 $6 2 kg 3 $18 5 kg 4 $22 6 kg 5 $28 7 kg knapsack instance (weight limit W = 11)
- 33. Which algorithm solves knapsack problem? A. Greedy-by-value: repeatedly add item with maximum vi. B. Greedy-by-weight: repeatedly add item with minimum wi. C. Greedy-by-ratio: repeatedly add item with maximum ratio vi / wi. D. None of the above. 33 Dynamic programming: quiz 2 Creative Commons Attribution-Share Alike 2.5 by Dake $28 7 kg $22 6 kg $6 2 kg $1 1 kg $18 5 kg 11 kg i vi wi 1 $1 1 kg 2 $6 2 kg 3 $18 5 kg 4 $22 6 kg 5 $28 7 kg knapsack instance (weight limit W = 11)
- 34. Which subproblems? A. OPT(w) = optimal value of knapsack problem with weight limit w. B. OPT(i) = optimal value of knapsack problem with items 1, …, i. C. OPT(i, w) = optimal value of knapsack problem with items 1, …, i subject to weight limit w. D. Any of the above. 34 Dynamic programming: quiz 3
- 35. Dynamic programming: two variables Def. OPT(i, w) = optimal value of knapsack problem with items 1, …, i, subject to weight limit w. Goal. OPT(n, W). Case 1. OPT(i, w) does not select item i. ・OPT(i, w) selects best of { 1, 2, …, i – 1 } subject to weight limit w. Case 2. OPT(i, w) selects item i. ・Collect value vi. ・New weight limit = w – wi. ・OPT(i, w) selects best of { 1, 2, …, i – 1 } subject to new weight limit. Bellman equation. 35 optimal substructure property (proof via exchange argument) possibly because wi > w OPT(i, w) = 0 B7 i = 0 OPT(i 1, w) B7 wi > w max { OPT(i 1, w), vi + OPT(i 1, w wi) } Qi?2`rBb2 <latexit sha1_base64="yGc+dBk4QwRLdPr1J0EKEi2YjzI=">AAADBHicbVFNb9NAEF2brxK+0nLkMiICFZFGNkKlKCoq4sKNIDW0UjaK1puxs+p67e6um0RWzvwaTogr/wPxZ1i7OTgpI6309Gbem9mZKJfC2CD44/m3bt+5e2/nfuvBw0ePn7R3976ZrNAchzyTmT6PmEEpFA6tsBLPc40sjSSeRRefqvzZFWojMnVqlzmOU5YoEQvOrKMm7b9fBqf7ogvzV0D7x7TfohEmQpXceZpVi/YDeAnU4sJCCSKGFQg4hgAoHfUOMR27itrhIKw9tmrnEwEfYN6spilbAJUYW6Cl6wkNeRdot6KunOx1I3HgfKr5gGqRzJxw1WiU2RnquTDo+lHaoqim6+kn7U7QC+qAmyBcgw5Zx2Cy6+3RacaLFJXlkhkzCoPcjkumreAS3ToKgznjFyzBkYOKpWjGZX2FFbxwzBTiTLunLNRsU1Gy1JhlGrnKlNmZ2c5V5P9yo8LGR+NSqLywqPh1o7iQYDOoTgpToZFbuXSAcS3crMBnTDNu3eE3utTeOfKNn5SLQgmeTXGLlXZhNau2GG7v7CYYvum974Vf33ZOjtbr3CHPyHOyT0LyjpyQz2RAhoR7H73Ey71L/7v/w//p/7ou9b215inZCP/3P7Vj6Os=</latexit> <latexit sha1_base64="yGc+dBk4QwRLdPr1J0EKEi2YjzI=">AAADBHicbVFNb9NAEF2brxK+0nLkMiICFZFGNkKlKCoq4sKNIDW0UjaK1puxs+p67e6um0RWzvwaTogr/wPxZ1i7OTgpI6309Gbem9mZKJfC2CD44/m3bt+5e2/nfuvBw0ePn7R3976ZrNAchzyTmT6PmEEpFA6tsBLPc40sjSSeRRefqvzZFWojMnVqlzmOU5YoEQvOrKMm7b9fBqf7ogvzV0D7x7TfohEmQpXceZpVi/YDeAnU4sJCCSKGFQg4hgAoHfUOMR27itrhIKw9tmrnEwEfYN6spilbAJUYW6Cl6wkNeRdot6KunOx1I3HgfKr5gGqRzJxw1WiU2RnquTDo+lHaoqim6+kn7U7QC+qAmyBcgw5Zx2Cy6+3RacaLFJXlkhkzCoPcjkumreAS3ToKgznjFyzBkYOKpWjGZX2FFbxwzBTiTLunLNRsU1Gy1JhlGrnKlNmZ2c5V5P9yo8LGR+NSqLywqPh1o7iQYDOoTgpToZFbuXSAcS3crMBnTDNu3eE3utTeOfKNn5SLQgmeTXGLlXZhNau2GG7v7CYYvum974Vf33ZOjtbr3CHPyHOyT0LyjpyQz2RAhoR7H73Ey71L/7v/w//p/7ou9b215inZCP/3P7Vj6Os=</latexit> <latexit sha1_base64="yGc+dBk4QwRLdPr1J0EKEi2YjzI=">AAADBHicbVFNb9NAEF2brxK+0nLkMiICFZFGNkKlKCoq4sKNIDW0UjaK1puxs+p67e6um0RWzvwaTogr/wPxZ1i7OTgpI6309Gbem9mZKJfC2CD44/m3bt+5e2/nfuvBw0ePn7R3976ZrNAchzyTmT6PmEEpFA6tsBLPc40sjSSeRRefqvzZFWojMnVqlzmOU5YoEQvOrKMm7b9fBqf7ogvzV0D7x7TfohEmQpXceZpVi/YDeAnU4sJCCSKGFQg4hgAoHfUOMR27itrhIKw9tmrnEwEfYN6spilbAJUYW6Cl6wkNeRdot6KunOx1I3HgfKr5gGqRzJxw1WiU2RnquTDo+lHaoqim6+kn7U7QC+qAmyBcgw5Zx2Cy6+3RacaLFJXlkhkzCoPcjkumreAS3ToKgznjFyzBkYOKpWjGZX2FFbxwzBTiTLunLNRsU1Gy1JhlGrnKlNmZ2c5V5P9yo8LGR+NSqLywqPh1o7iQYDOoTgpToZFbuXSAcS3crMBnTDNu3eE3utTeOfKNn5SLQgmeTXGLlXZhNau2GG7v7CYYvum974Vf33ZOjtbr3CHPyHOyT0LyjpyQz2RAhoR7H73Ey71L/7v/w//p/7ou9b215inZCP/3P7Vj6Os=</latexit> <latexit sha1_base64="yGc+dBk4QwRLdPr1J0EKEi2YjzI=">AAADBHicbVFNb9NAEF2brxK+0nLkMiICFZFGNkKlKCoq4sKNIDW0UjaK1puxs+p67e6um0RWzvwaTogr/wPxZ1i7OTgpI6309Gbem9mZKJfC2CD44/m3bt+5e2/nfuvBw0ePn7R3976ZrNAchzyTmT6PmEEpFA6tsBLPc40sjSSeRRefqvzZFWojMnVqlzmOU5YoEQvOrKMm7b9fBqf7ogvzV0D7x7TfohEmQpXceZpVi/YDeAnU4sJCCSKGFQg4hgAoHfUOMR27itrhIKw9tmrnEwEfYN6spilbAJUYW6Cl6wkNeRdot6KunOx1I3HgfKr5gGqRzJxw1WiU2RnquTDo+lHaoqim6+kn7U7QC+qAmyBcgw5Zx2Cy6+3RacaLFJXlkhkzCoPcjkumreAS3ToKgznjFyzBkYOKpWjGZX2FFbxwzBTiTLunLNRsU1Gy1JhlGrnKlNmZ2c5V5P9yo8LGR+NSqLywqPh1o7iQYDOoTgpToZFbuXSAcS3crMBnTDNu3eE3utTeOfKNn5SLQgmeTXGLlXZhNau2GG7v7CYYvum974Vf33ZOjtbr3CHPyHOyT0LyjpyQz2RAhoR7H73Ey71L/7v/w//p/7ou9b215inZCP/3P7Vj6Os=</latexit>
- 36. Knapsack problem: bottom-up dynamic programming 36 KNAPSACK(n, W, w1, …, wn, v1, …, vn ) __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ FOR w = 0 TO W M[0, w] ← 0. FOR i = 1 TO n FOR w = 0 TO W IF (wi > w) M[i, w] ← M[i – 1, w]. ELSE M[i, w] ← max { M[i – 1, w], vi + M[i – 1, w – wi] }. RETURN M[n, W]. __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ previously computed values OPT(i, w) = 0 B7 i = 0 OPT(i 1, w) B7 wi > w max { OPT(i 1, w), vi + OPT(i 1, w wi) } Qi?2`rBb2 <latexit sha1_base64="yGc+dBk4QwRLdPr1J0EKEi2YjzI=">AAADBHicbVFNb9NAEF2brxK+0nLkMiICFZFGNkKlKCoq4sKNIDW0UjaK1puxs+p67e6um0RWzvwaTogr/wPxZ1i7OTgpI6309Gbem9mZKJfC2CD44/m3bt+5e2/nfuvBw0ePn7R3976ZrNAchzyTmT6PmEEpFA6tsBLPc40sjSSeRRefqvzZFWojMnVqlzmOU5YoEQvOrKMm7b9fBqf7ogvzV0D7x7TfohEmQpXceZpVi/YDeAnU4sJCCSKGFQg4hgAoHfUOMR27itrhIKw9tmrnEwEfYN6spilbAJUYW6Cl6wkNeRdot6KunOx1I3HgfKr5gGqRzJxw1WiU2RnquTDo+lHaoqim6+kn7U7QC+qAmyBcgw5Zx2Cy6+3RacaLFJXlkhkzCoPcjkumreAS3ToKgznjFyzBkYOKpWjGZX2FFbxwzBTiTLunLNRsU1Gy1JhlGrnKlNmZ2c5V5P9yo8LGR+NSqLywqPh1o7iQYDOoTgpToZFbuXSAcS3crMBnTDNu3eE3utTeOfKNn5SLQgmeTXGLlXZhNau2GG7v7CYYvum974Vf33ZOjtbr3CHPyHOyT0LyjpyQz2RAhoR7H73Ey71L/7v/w//p/7ou9b215inZCP/3P7Vj6Os=</latexit> <latexit sha1_base64="yGc+dBk4QwRLdPr1J0EKEi2YjzI=">AAADBHicbVFNb9NAEF2brxK+0nLkMiICFZFGNkKlKCoq4sKNIDW0UjaK1puxs+p67e6um0RWzvwaTogr/wPxZ1i7OTgpI6309Gbem9mZKJfC2CD44/m3bt+5e2/nfuvBw0ePn7R3976ZrNAchzyTmT6PmEEpFA6tsBLPc40sjSSeRRefqvzZFWojMnVqlzmOU5YoEQvOrKMm7b9fBqf7ogvzV0D7x7TfohEmQpXceZpVi/YDeAnU4sJCCSKGFQg4hgAoHfUOMR27itrhIKw9tmrnEwEfYN6spilbAJUYW6Cl6wkNeRdot6KunOx1I3HgfKr5gGqRzJxw1WiU2RnquTDo+lHaoqim6+kn7U7QC+qAmyBcgw5Zx2Cy6+3RacaLFJXlkhkzCoPcjkumreAS3ToKgznjFyzBkYOKpWjGZX2FFbxwzBTiTLunLNRsU1Gy1JhlGrnKlNmZ2c5V5P9yo8LGR+NSqLywqPh1o7iQYDOoTgpToZFbuXSAcS3crMBnTDNu3eE3utTeOfKNn5SLQgmeTXGLlXZhNau2GG7v7CYYvum974Vf33ZOjtbr3CHPyHOyT0LyjpyQz2RAhoR7H73Ey71L/7v/w//p/7ou9b215inZCP/3P7Vj6Os=</latexit> <latexit sha1_base64="yGc+dBk4QwRLdPr1J0EKEi2YjzI=">AAADBHicbVFNb9NAEF2brxK+0nLkMiICFZFGNkKlKCoq4sKNIDW0UjaK1puxs+p67e6um0RWzvwaTogr/wPxZ1i7OTgpI6309Gbem9mZKJfC2CD44/m3bt+5e2/nfuvBw0ePn7R3976ZrNAchzyTmT6PmEEpFA6tsBLPc40sjSSeRRefqvzZFWojMnVqlzmOU5YoEQvOrKMm7b9fBqf7ogvzV0D7x7TfohEmQpXceZpVi/YDeAnU4sJCCSKGFQg4hgAoHfUOMR27itrhIKw9tmrnEwEfYN6spilbAJUYW6Cl6wkNeRdot6KunOx1I3HgfKr5gGqRzJxw1WiU2RnquTDo+lHaoqim6+kn7U7QC+qAmyBcgw5Zx2Cy6+3RacaLFJXlkhkzCoPcjkumreAS3ToKgznjFyzBkYOKpWjGZX2FFbxwzBTiTLunLNRsU1Gy1JhlGrnKlNmZ2c5V5P9yo8LGR+NSqLywqPh1o7iQYDOoTgpToZFbuXSAcS3crMBnTDNu3eE3utTeOfKNn5SLQgmeTXGLlXZhNau2GG7v7CYYvum974Vf33ZOjtbr3CHPyHOyT0LyjpyQz2RAhoR7H73Ey71L/7v/w//p/7ou9b215inZCP/3P7Vj6Os=</latexit> <latexit sha1_base64="yGc+dBk4QwRLdPr1J0EKEi2YjzI=">AAADBHicbVFNb9NAEF2brxK+0nLkMiICFZFGNkKlKCoq4sKNIDW0UjaK1puxs+p67e6um0RWzvwaTogr/wPxZ1i7OTgpI6309Gbem9mZKJfC2CD44/m3bt+5e2/nfuvBw0ePn7R3976ZrNAchzyTmT6PmEEpFA6tsBLPc40sjSSeRRefqvzZFWojMnVqlzmOU5YoEQvOrKMm7b9fBqf7ogvzV0D7x7TfohEmQpXceZpVi/YDeAnU4sJCCSKGFQg4hgAoHfUOMR27itrhIKw9tmrnEwEfYN6spilbAJUYW6Cl6wkNeRdot6KunOx1I3HgfKr5gGqRzJxw1WiU2RnquTDo+lHaoqim6+kn7U7QC+qAmyBcgw5Zx2Cy6+3RacaLFJXlkhkzCoPcjkumreAS3ToKgznjFyzBkYOKpWjGZX2FFbxwzBTiTLunLNRsU1Gy1JhlGrnKlNmZ2c5V5P9yo8LGR+NSqLywqPh1o7iQYDOoTgpToZFbuXSAcS3crMBnTDNu3eE3utTeOfKNn5SLQgmeTXGLlXZhNau2GG7v7CYYvum974Vf33ZOjtbr3CHPyHOyT0LyjpyQz2RAhoR7H73Ey71L/7v/w//p/7ou9b215inZCP/3P7Vj6Os=</latexit>
- 37. Knapsack problem: bottom-up dynamic programming demo 37 0 1 2 3 4 5 6 7 8 9 10 11 { } 0 0 0 0 0 0 0 0 0 0 0 0 { 1 } 0 1 1 1 1 1 1 1 1 1 1 1 { 1, 2 } 0 1 6 7 7 7 7 7 7 7 7 7 { 1, 2, 3 } 0 1 6 7 7 18 19 24 25 25 25 25 { 1, 2, 3, 4 } 0 1 6 7 7 18 22 24 28 29 29 40 { 1, 2, 3, 4, 5 } 0 1 6 7 7 18 22 28 29 34 35 40 weight limit w subset of items 1, …, i OPT(i, w) = optimal value of knapsack problem with items 1, …, i, subject to weight limit w OPT(i, w) = 0 B7 i = 0 OPT(i 1, w) B7 wi > w max {OPT(i 1, w), vi + OPT(i 1, w wi} Qi?2`rBb2 <latexit sha1_base64="Z2vromkJx+wQ2wpWsn/gLtchm2Q=">AAAC+nicbVFda9swFJW9ry77SrvHvVwWNjqWBnuMtSN0FPayt2XQrIXIBFm5TkRl2Uhyk2D8a/Y09ro/ssf9m8luHpx0FwSHc889VzqKcymMDYK/nn/n7r37D/Yedh49fvL0WXf/4LvJCs1xzDOZ6cuYGZRC4dgKK/Ey18jSWOJFfPW57l9cozYiU+d2nWOUsrkSieDMOmra/fN1dH4o+rB8A3R4SocdGuNcqJI7T1N16DCA10AtriyUIBKoQMApBEDpZPAB08gpGoejsPHY0S6nAj7Bsq2mKVsBlZhYoCW0ZvtA+3DtBt622KPagWoxXzh51bLP7AL1Uhh0WyjtUFSzzZ2n3V4wCJqC2yDcgB7Z1Gi67x3QWcaLFJXlkhkzCYPcRiXTVnCJLoTCYM74FZvjxEHFUjRR2WRfwSvHzCDJtDvKQsO2J0qWGrNOY6dMmV2Y3V5N/q83KWxyEpVC5YVFxW8WJYUEm0H9kTATGrmVawcY18LdFfiCacat++6tLY13jnzrJeWqUIJnM9xhpV1ZzeoUw93MboPxu8HHQfjtfe/sZBPnHnlBXpJDEpJjcka+kBEZE+4de5GXeHO/8n/4P/1fN1Lf28w8J1vl//4H1VHmOQ==</latexit> <latexit sha1_base64="Z2vromkJx+wQ2wpWsn/gLtchm2Q=">AAAC+nicbVFda9swFJW9ry77SrvHvVwWNjqWBnuMtSN0FPayt2XQrIXIBFm5TkRl2Uhyk2D8a/Y09ro/ssf9m8luHpx0FwSHc889VzqKcymMDYK/nn/n7r37D/Yedh49fvL0WXf/4LvJCs1xzDOZ6cuYGZRC4dgKK/Ey18jSWOJFfPW57l9cozYiU+d2nWOUsrkSieDMOmra/fN1dH4o+rB8A3R4SocdGuNcqJI7T1N16DCA10AtriyUIBKoQMApBEDpZPAB08gpGoejsPHY0S6nAj7Bsq2mKVsBlZhYoCW0ZvtA+3DtBt622KPagWoxXzh51bLP7AL1Uhh0WyjtUFSzzZ2n3V4wCJqC2yDcgB7Z1Gi67x3QWcaLFJXlkhkzCYPcRiXTVnCJLoTCYM74FZvjxEHFUjRR2WRfwSvHzCDJtDvKQsO2J0qWGrNOY6dMmV2Y3V5N/q83KWxyEpVC5YVFxW8WJYUEm0H9kTATGrmVawcY18LdFfiCacat++6tLY13jnzrJeWqUIJnM9xhpV1ZzeoUw93MboPxu8HHQfjtfe/sZBPnHnlBXpJDEpJjcka+kBEZE+4de5GXeHO/8n/4P/1fN1Lf28w8J1vl//4H1VHmOQ==</latexit> <latexit sha1_base64="Z2vromkJx+wQ2wpWsn/gLtchm2Q=">AAAC+nicbVFda9swFJW9ry77SrvHvVwWNjqWBnuMtSN0FPayt2XQrIXIBFm5TkRl2Uhyk2D8a/Y09ro/ssf9m8luHpx0FwSHc889VzqKcymMDYK/nn/n7r37D/Yedh49fvL0WXf/4LvJCs1xzDOZ6cuYGZRC4dgKK/Ey18jSWOJFfPW57l9cozYiU+d2nWOUsrkSieDMOmra/fN1dH4o+rB8A3R4SocdGuNcqJI7T1N16DCA10AtriyUIBKoQMApBEDpZPAB08gpGoejsPHY0S6nAj7Bsq2mKVsBlZhYoCW0ZvtA+3DtBt622KPagWoxXzh51bLP7AL1Uhh0WyjtUFSzzZ2n3V4wCJqC2yDcgB7Z1Gi67x3QWcaLFJXlkhkzCYPcRiXTVnCJLoTCYM74FZvjxEHFUjRR2WRfwSvHzCDJtDvKQsO2J0qWGrNOY6dMmV2Y3V5N/q83KWxyEpVC5YVFxW8WJYUEm0H9kTATGrmVawcY18LdFfiCacat++6tLY13jnzrJeWqUIJnM9xhpV1ZzeoUw93MboPxu8HHQfjtfe/sZBPnHnlBXpJDEpJjcka+kBEZE+4de5GXeHO/8n/4P/1fN1Lf28w8J1vl//4H1VHmOQ==</latexit> <latexit sha1_base64="Z2vromkJx+wQ2wpWsn/gLtchm2Q=">AAAC+nicbVFda9swFJW9ry77SrvHvVwWNjqWBnuMtSN0FPayt2XQrIXIBFm5TkRl2Uhyk2D8a/Y09ro/ssf9m8luHpx0FwSHc889VzqKcymMDYK/nn/n7r37D/Yedh49fvL0WXf/4LvJCs1xzDOZ6cuYGZRC4dgKK/Ey18jSWOJFfPW57l9cozYiU+d2nWOUsrkSieDMOmra/fN1dH4o+rB8A3R4SocdGuNcqJI7T1N16DCA10AtriyUIBKoQMApBEDpZPAB08gpGoejsPHY0S6nAj7Bsq2mKVsBlZhYoCW0ZvtA+3DtBt622KPagWoxXzh51bLP7AL1Uhh0WyjtUFSzzZ2n3V4wCJqC2yDcgB7Z1Gi67x3QWcaLFJXlkhkzCYPcRiXTVnCJLoTCYM74FZvjxEHFUjRR2WRfwSvHzCDJtDvKQsO2J0qWGrNOY6dMmV2Y3V5N/q83KWxyEpVC5YVFxW8WJYUEm0H9kTATGrmVawcY18LdFfiCacat++6tLY13jnzrJeWqUIJnM9xhpV1ZzeoUw93MboPxu8HHQfjtfe/sZBPnHnlBXpJDEpJjcka+kBEZE+4de5GXeHO/8n/4P/1fN1Lf28w8J1vl//4H1VHmOQ==</latexit> i vi wi 1 $1 1 kg 2 $6 2 kg 3 $18 5 kg 4 $22 6 kg 5 $28 7 kg
- 38. Knapsack problem: running time Theorem. The DP algorithm solves the knapsack problem with n items and maximum weight W in Θ(n W) time and Θ(n W) space. Pf. ・Takes O(1) time per table entry. ・There are Θ(n W) table entries. ・After computing optimal values, can trace back to find solution: OPT(i, w) takes item i iff M [i, w] > M [i – 1, w]. ▪ Remarks. ・Algorithm depends critically on assumption that weights are integral. ・Assumption that values are integral was not used. 38 weights are integers between 1 and W
- 39. Does there exist a poly-time algorithm for the knapsack problem? A. Yes, because the DP algorithm takes Θ(n W) time. B. No, because Θ(n W) is not a polynomial function of the input size. C. No, because the problem is NP-hard. D. Unknown. 39 Dynamic programming: quiz 4 “pseudo-polynomial” equivalent to P ≠ NP conjecture because knapsack problem is NP-hard
- 40. COIN CHANGING Problem. Given n coin denominations { d1, d2, …, dn } and a target value V, find the fewest coins needed to make change for V (or report impossible). Recall. Greedy cashier’s algorithm is optimal for U.S. coin denominations, but not for arbitrary coin denominations. Ex. { 1, 10, 21, 34, 70, 100, 350, 1295, 1500 }. Optimal. 140¢ = 70 + 70. 40
- 41. Def. OPT(v) = min number of coins to make change for v. Goal. OPT(V). Multiway choice. To compute OPT(v), ・Select a coin of denomination ci for some i. ・Select fewest coins to make change for v – ci. Bellman equation. Running time. O(n V). COIN CHANGING 41 optimal substructure property (proof via exchange argument) <latexit sha1_base64="6B5tGCszYw5e5nluRWvumveoBFs=">AAAC/HicbVFNb9NAEF2brxI+mpYjlxERqAgR2QjaSKGoEhduBKlpK2VDtF6Pk1XXa8s7jhJZ4ddwQ1z5Idz4N6zdHEjCSPY+v3m78/w2yrWyFAR/PP/W7Tt37+3dbz14+Ojxfvvg8MJmZSFxKDOdFVeRsKiVwSEp0niVFyjSSONldP2x7l/OsbAqM+e0zHGciqlRiZKCHDVp//48OD+avwTeP+X9Fo9wqkwl3YF21eJ9rkxCS4AXwAkXBBWoBFYwh/cQAOej7jGmY6dzX7ua000NT5XhWqWK7KQKgWsE1bzNql4SAl45GxDCK2hMwWuIJ6q2BrxQ05kTrHanfGimtDiaeO170u4E3aAp2AXhGnTYugaTA++Qx5ksUzQktbB2FAY5jStRkJIaXRClxVzIazHFkYNGpGjHVRP+Cp47JoYkK9xjCBr23x2VSK1dppFTpoJmdrtXk//rjUpKeuNKmbwkNPJmUFJqoAzqm4RYFShJLx0QslDOK8iZKIQkd98bU5qzc5Qbf1ItSqNkFuMWq2lBhahTDLcz2wUXb7rhu27w5W3nrLfOc489Zc/YEQvZCTtjn9iADZn0et5Xb+rN/G/+d/+H//NG6nvrPU/YRvm//gIVIecP</latexit> OPT(v) = 8 > > > > < > > > > : 1 B7 v < 0 0 B7 v = 0 min 1in { 1 + OPT(v di) } B7 v > 0
- 42. 6. DYNAMIC PROGRAMMING I ‣ weighted interval scheduling ‣ segmented least squares ‣ knapsack problem ‣ RNA secondary structure SECTION 6.5
- 43. RNA secondary structure RNA. String B = b1b2…bn over alphabet { A, C, G, U }. Secondary structure. RNA is single-stranded so it tends to loop back and form base pairs with itself. This structure is essential for understanding behavior of molecule. G U C A G A A G C G A U G A U U A G A C A A C U G A G U C A U C G G G C C G RNA secondary structure for GUCGAUUGAGCGAAUGUAACAACGUGGCUACGGCGAGA 43 base base pair
- 44. Secondary structure. A set of pairs S = { (bi, bj) } that satisfy: ・[Watson–Crick] S is a matching and each pair in S is a Watson–Crick complement: A–U, U–A, C–G, or G–C. RNA secondary structure 44 A C G U G G C C A U S is not a secondary structure (C-A is not a valid Watson-Crick pair) B = ACGUGGCCCAU S = { (b1, b10), (b2, b9), (b3, b8) } base pair in secondary structure C G G C A G C U U A
- 45. Secondary structure. A set of pairs S = { (bi, bj) } that satisfy: ・[Watson–Crick] S is a matching and each pair in S is a Watson–Crick complement: A–U, U–A, C–G, or G–C. ・[No sharp turns] The ends of each pair are separated by at least 4 intervening bases. If (bi, bj) ∈ S, then i < j – 4. RNA secondary structure 45 G G C A G U U A G A U G G G C A U S is not a secondary structure (≤4 intervening bases between G and C) G B = AUGGGGCAU S = { (b1, b9), (b2, b8), (b3, b7) }
- 46. Secondary structure. A set of pairs S = { (bi, bj) } that satisfy: ・[Watson–Crick] S is a matching and each pair in S is a Watson–Crick complement: A–U, U–A, C–G, or G–C. ・[No sharp turns] The ends of each pair are separated by at least 4 intervening bases. If (bi, bj) ∈ S, then i < j – 4. ・[Non-crossing] If (bi, bj) and (bk, bℓ) are two pairs in S, then we cannot have i < k < j < ℓ. RNA secondary structure 46 A G U U G G C C A U S is not a secondary structure (G-C and U-A cross) C G G C A U G U U A B = ACUUGGCCAU S = { (b1, b10), (b2, b8), (b3, b9) }
- 47. Secondary structure. A set of pairs S = { (bi, bj) } that satisfy: ・[Watson–Crick] S is a matching and each pair in S is a Watson–Crick complement: A–U, U–A, C–G, or G–C. ・[No sharp turns] The ends of each pair are separated by at least 4 intervening bases. If (bi, bj) ∈ S, then i < j – 4. ・[Non-crossing] If (bi, bj) and (bk, bℓ) are two pairs in S, then we cannot have i < k < j < ℓ. RNA secondary structure 47 A U G U G G C C A U S is a secondary structure (with 3 base pairs) C G G C A G U U U A B = AUGUGGCCAU S = { (b1, b10), (b2, b9), (b3, b8) }
- 48. RNA secondary structure Secondary structure. A set of pairs S = { (bi, bj) } that satisfy: ・[Watson–Crick] S is a matching and each pair in S is a Watson–Crick complement: A–U, U–A, C–G, or G–C. ・[No sharp turns] The ends of each pair are separated by at least 4 intervening bases. If (bi, bj) ∈ S, then i < j – 4. ・[Non-crossing] If (bi, bj) and (bk, bℓ) are two pairs in S, then we cannot have i < k < j < ℓ. Free-energy hypothesis. RNA molecule will form the secondary structure with the minimum total free energy. Goal. Given an RNA molecule B = b1b2…bn, find a secondary structure S that maximizes the number of base pairs. approximate by number of base pairs (more base pairs ⇒ lower free energy) 48
- 49. Is the following a secondary structure? A. Yes. B. No, violates Watson–Crick condition. C. No, violates no-sharp-turns condition. D. No, violates no-crossing condition. 49 Dynamic programming: quiz 5 G U C A G A A G C G A U G A U U A G C G U G C C G
- 50. Which subproblems? A. OPT(j) = max number of base pairs in secondary structure of the substring b1b2 … bj. B. OPT(j) = max number of base pairs in secondary structure of the substring bj bj+1 … bn. C. Either A or B. D. Neither A nor B. 50 Dynamic programming: quiz 6
- 51. RNA secondary structure: subproblems First attempt. OPT(j) = maximum number of base pairs in a secondary structure of the substring b1b2 … bj. Goal. OPT(n). Choice. Match bases bt and bj. Difficulty. Results in two subproblems (but one of wrong form). ・Find secondary structure in b1b2 … bt–1. ・Find secondary structure in bt+1bt+2 … bj–1. OPT(t–1) need more subproblems (first base no longer b1) 51 1 t j match bases bt and bn last base
- 52. Dynamic programming over intervals Def. OPT(i, j) = maximum number of base pairs in a secondary structure of the substring bi bi+1 … bj. Case 1. If i ≥ j – 4. ・OPT(i, j) = 0 by no-sharp-turns condition. Case 2. Base bj is not involved in a pair. ・OPT(i, j) = OPT(i, j – 1). Case 3. Base bj pairs with bt for some i ≤ t < j – 4. ・Non-crossing condition decouples resulting two subproblems. ・OPT(i, j) = 1 + max t { OPT(i, t – 1) + OPT(t + 1, j – 1) }. take max over t such that i ≤ t < j – 4 and bt and bj are Watson–Crick complements 52 i t j match bases bj and bt
- 53. In which order to compute OPT(i, j) ? A. Increasing i, then j. B. Increasing j, then i. C. Either A or B. D. Neither A nor B. 53 Dynamic programming: quiz 7 i t j match bases bj and bt OPT(i, j) depends upon OPT(i, t-1) and OPT(t+1, j-1)
- 54. Bottom-up dynamic programming over intervals Q. In which order to solve the subproblems? A. Do shortest intervals first—increasing order of ⎜j − i⎟. Theorem. The DP algorithm solves the RNA secondary structure problem in O(n3 ) time and O(n2 ) space. 54 6 7 8 9 10 4 0 0 0 3 0 0 2 0 1 i j order in which to solve subproblems RNA-SECONDARY-STRUCTURE(n, b1, …, bn ) __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ FOR k = 5 TO n – 1 FOR i = 1 TO n – k j ← i + k. Compute M[i, j] using formula. RETURN M[1, n]. __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ all needed values are already computed
- 55. Dynamic programming summary Outline. ・Define a collection of subproblems. ・Solution to original problem can be computed from subproblems. ・Natural ordering of subproblems from “smallest” to “largest” that enables determining a solution to a subproblem from solutions to smaller subproblems. Techniques. ・Binary choice: weighted interval scheduling. ・Multiway choice: segmented least squares. ・Adding a new variable: knapsack problem. ・Intervals: RNA secondary structure. Top-down vs. bottom-up dynamic programming. Opinions differ. 55 typically, only a polynomial number of subproblems






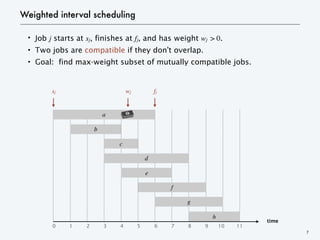



![Weighted interval scheduling: brute force
11
BRUTE-FORCE (n, s1, …, sn, f1, …, fn, w1, …, wn)
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Sort jobs by finish time and renumber so that f1 ≤ f2 ≤ … ≤ fn.
Compute p[1], p[2], …, p[n] via binary search.
RETURN COMPUTE-OPT(n).
COMPUTE-OPT( j )
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
IF (j = 0)
RETURN 0.
ELSE
RETURN max {COMPUTE-OPT( j – 1), wj + COMPUTE-OPT(p[ j ]) }.](https://image.slidesharecdn.com/06dynamicprogrammingi-240815151754-56ae93ab/85/06DynamicProgramming-in-algorithms-CSE-pdf-11-320.jpg)
![What is running time of COMPUTE-OPT(n) in the worst case?
A. Θ(n log n)
B. Θ(n2
)
C. Θ(1.618n
)
D. Θ(2n
)
12
Dynamic programming: quiz 1
COMPUTE-OPT( j )
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
IF (j = 0)
RETURN 0.
ELSE
RETURN max {COMPUTE-OPT( j – 1), wj + COMPUTE-OPT(p[ j ]) }.
T(n) =
(1) B7 n = 1
2T(n 1) + (1) B7 n > 1
<latexit sha1_base64="eY4cuuNdtPSoc87X0TvZnXEtJMc=">AAACsXicdVFtaxNBEN4732p8S6vfRBlMlZRiuCuFVopS8IsfKyS2mDvi3t5csmRv79idk4Qj3/2L/gl/g3vpCSbVgV0enpl5ZvbZpFTSUhD89Pxbt+/cvbdzv/Pg4aPHT7q7e19sURmBI1Gowlwl3KKSGkckSeFVaZDnicLLZP6xyV9+R2NloYe0LDHO+VTLTApOjpp0fwz7+gCiM3jfXJ0owanUtXCKdtWJzqLhDIn3wwN4AxHhgmqQGexrVx7uwwqiaDw4wTx2pUdOCd5C2KgdOi34b++HP72dCHXaDpt0e8EgWAfcBGELeqyNi8mutxelhahy1CQUt3YcBiXFNTckhUK3fWWx5GLOpzh2UPMcbVyvLVvBa8ekkBXGHU2wZv/uqHlu7TJPXGXOaWa3cw35r9y4ouw0rqUuK0ItrgdllQIqoPEfUmlQkFo6wIWRblcQM264IPdLG1PW2iWKjZfUi0pLUaS4xSpakOGNi+G2ZzfB6GjwbhB+Pu6dn7Z27rDn7BXrs5CdsHP2iV2wERPsl/fMe+G99I/9r/43P7ku9b225ynbCH/+G90py9g=</latexit>
<latexit sha1_base64="eY4cuuNdtPSoc87X0TvZnXEtJMc=">AAACsXicdVFtaxNBEN4732p8S6vfRBlMlZRiuCuFVopS8IsfKyS2mDvi3t5csmRv79idk4Qj3/2L/gl/g3vpCSbVgV0enpl5ZvbZpFTSUhD89Pxbt+/cvbdzv/Pg4aPHT7q7e19sURmBI1Gowlwl3KKSGkckSeFVaZDnicLLZP6xyV9+R2NloYe0LDHO+VTLTApOjpp0fwz7+gCiM3jfXJ0owanUtXCKdtWJzqLhDIn3wwN4AxHhgmqQGexrVx7uwwqiaDw4wTx2pUdOCd5C2KgdOi34b++HP72dCHXaDpt0e8EgWAfcBGELeqyNi8mutxelhahy1CQUt3YcBiXFNTckhUK3fWWx5GLOpzh2UPMcbVyvLVvBa8ekkBXGHU2wZv/uqHlu7TJPXGXOaWa3cw35r9y4ouw0rqUuK0ItrgdllQIqoPEfUmlQkFo6wIWRblcQM264IPdLG1PW2iWKjZfUi0pLUaS4xSpakOGNi+G2ZzfB6GjwbhB+Pu6dn7Z27rDn7BXrs5CdsHP2iV2wERPsl/fMe+G99I/9r/43P7ku9b225ynbCH/+G90py9g=</latexit>
<latexit sha1_base64="eY4cuuNdtPSoc87X0TvZnXEtJMc=">AAACsXicdVFtaxNBEN4732p8S6vfRBlMlZRiuCuFVopS8IsfKyS2mDvi3t5csmRv79idk4Qj3/2L/gl/g3vpCSbVgV0enpl5ZvbZpFTSUhD89Pxbt+/cvbdzv/Pg4aPHT7q7e19sURmBI1Gowlwl3KKSGkckSeFVaZDnicLLZP6xyV9+R2NloYe0LDHO+VTLTApOjpp0fwz7+gCiM3jfXJ0owanUtXCKdtWJzqLhDIn3wwN4AxHhgmqQGexrVx7uwwqiaDw4wTx2pUdOCd5C2KgdOi34b++HP72dCHXaDpt0e8EgWAfcBGELeqyNi8mutxelhahy1CQUt3YcBiXFNTckhUK3fWWx5GLOpzh2UPMcbVyvLVvBa8ekkBXGHU2wZv/uqHlu7TJPXGXOaWa3cw35r9y4ouw0rqUuK0ItrgdllQIqoPEfUmlQkFo6wIWRblcQM264IPdLG1PW2iWKjZfUi0pLUaS4xSpakOGNi+G2ZzfB6GjwbhB+Pu6dn7Z27rDn7BXrs5CdsHP2iV2wERPsl/fMe+G99I/9r/43P7ku9b225ynbCH/+G90py9g=</latexit>
<latexit sha1_base64="eY4cuuNdtPSoc87X0TvZnXEtJMc=">AAACsXicdVFtaxNBEN4732p8S6vfRBlMlZRiuCuFVopS8IsfKyS2mDvi3t5csmRv79idk4Qj3/2L/gl/g3vpCSbVgV0enpl5ZvbZpFTSUhD89Pxbt+/cvbdzv/Pg4aPHT7q7e19sURmBI1Gowlwl3KKSGkckSeFVaZDnicLLZP6xyV9+R2NloYe0LDHO+VTLTApOjpp0fwz7+gCiM3jfXJ0owanUtXCKdtWJzqLhDIn3wwN4AxHhgmqQGexrVx7uwwqiaDw4wTx2pUdOCd5C2KgdOi34b++HP72dCHXaDpt0e8EgWAfcBGELeqyNi8mutxelhahy1CQUt3YcBiXFNTckhUK3fWWx5GLOpzh2UPMcbVyvLVvBa8ekkBXGHU2wZv/uqHlu7TJPXGXOaWa3cw35r9y4ouw0rqUuK0ItrgdllQIqoPEfUmlQkFo6wIWRblcQM264IPdLG1PW2iWKjZfUi0pLUaS4xSpakOGNi+G2ZzfB6GjwbhB+Pu6dn7Z27rDn7BXrs5CdsHP2iV2wERPsl/fMe+G99I/9r/43P7ku9b225ynbCH/+G90py9g=</latexit>](https://image.slidesharecdn.com/06dynamicprogrammingi-240815151754-56ae93ab/85/06DynamicProgramming-in-algorithms-CSE-pdf-12-320.jpg)

![Weighted interval scheduling: memoization
Top-down dynamic programming (memoization).
・Cache result of subproblem j in M[j].
・Use M[j] to avoid solving subproblem j more than once.
14
M-COMPUTE-OPT( j )
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
IF (M[j] is uninitialized)
M[j] ← max { M-COMPUTE-OPT (j – 1), wj + M-COMPUTE-OPT(p[j]) }.
RETURN M[j].
TOP-DOWN(n, s1, …, sn, f1, …, fn, w1, …, wn)
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Sort jobs by finish time and renumber so that f1 ≤ f2 ≤ … ≤ fn.
Compute p[1], p[2], …, p[n] via binary search.
M[0] ← 0.
RETURN M-COMPUTE-OPT(n).
global array](https://image.slidesharecdn.com/06dynamicprogrammingi-240815151754-56ae93ab/85/06DynamicProgramming-in-algorithms-CSE-pdf-14-320.jpg)
![Weighted interval scheduling: running time
Claim. Memoized version of algorithm takes O(n log n) time.
Pf.
・Sort by finish time: O(n log n) via mergesort.
・Compute p[j] for each j : O(n log n) via binary search.
・M-COMPUTE-OPT(j): each invocation takes O(1) time and either
- (1) returns an initialized value M[j]
- (2) initializes M[j] and makes two recursive calls
・Progress measure Φ = # initialized entries among M[1.. n].
- initially Φ = 0; throughout Φ ≤ n.
- (2) increases Φ by 1 ⇒ ≤ 2n recursive calls.
・Overall running time of M-COMPUTE-OPT(n) is O(n). ▪
15](https://image.slidesharecdn.com/06dynamicprogrammingi-240815151754-56ae93ab/85/06DynamicProgramming-in-algorithms-CSE-pdf-15-320.jpg)

![Weighted interval scheduling: finding a solution
Q. DP algorithm computes optimal value. How to find optimal solution?
A. Make a second pass by calling FIND-SOLUTION(n).
Analysis. # of recursive calls ≤ n ⇒ O(n).
17
FIND-SOLUTION(j)
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________
IF (j = 0)
RETURN ∅.
ELSE IF (wj + M[p[j]] > M[ j – 1])
RETURN { j } ∪ FIND-SOLUTION(p[j]).
ELSE
RETURN FIND-SOLUTION( j – 1).
M[j] = max { M[j – 1], wj + M[p[j]] }.](https://image.slidesharecdn.com/06dynamicprogrammingi-240815151754-56ae93ab/85/06DynamicProgramming-in-algorithms-CSE-pdf-17-320.jpg)
![Weighted interval scheduling: bottom-up dynamic programming
Bottom-up dynamic programming. Unwind recursion.
Running time. The bottom-up version takes O(n log n) time.
18
BOTTOM-UP(n, s1, …, sn, f1, …, fn, w1, …, wn)
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Sort jobs by finish time and renumber so that f1 ≤ f2 ≤ … ≤ fn.
Compute p[1], p[2], …, p[n].
M[0] ← 0.
FOR j = 1 TO n
M[j] ← max { M[ j – 1], wj + M[p[j]] }.
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
previously computed values](https://image.slidesharecdn.com/06dynamicprogrammingi-240815151754-56ae93ab/85/06DynamicProgramming-in-algorithms-CSE-pdf-18-320.jpg)

![MAXIMUM SUBARRAY PROBLEM
Goal. Given an array x of n integer (positive or negative),
find a contiguous subarray whose sum is maximum.
Brute-force algorithm.
・For each i and j : computer a[i] + a[i+1] + … + a[j].
・Takes Θ(n3
) time.
Apply “cumulative sum” trick.
・Precompute cumulative sums: S[i] = a[0] + a[1] + … + a[i].
・Now a[i] + a[i+1] + … + a[j] = S[j] − S[i−1].
・Improves running time Θ(n2
).
20
12 5 −1 31 −61 59 26 −53 58 97 −93 −23 84 −15 6
187
i j](https://image.slidesharecdn.com/06dynamicprogrammingi-240815151754-56ae93ab/85/06DynamicProgramming-in-algorithms-CSE-pdf-20-320.jpg)








![Segmented least squares algorithm
29
SEGMENTED-LEAST-SQUARES(n, p1, …, pn, c)
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
FOR j = 1 TO n
FOR i = 1 TO j
Compute the SSE eij for the points pi, pi+1, …, pj.
M[0] ← 0.
FOR j = 1 TO n
M[j] ← min 1 ≤ i ≤ j { eij + c + M[i – 1] }.
RETURN M[n].
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
previously computed value](https://image.slidesharecdn.com/06dynamicprogrammingi-240815151754-56ae93ab/85/06DynamicProgramming-in-algorithms-CSE-pdf-29-320.jpg)
![Segmented least squares analysis
Theorem. [Bellman 1961] DP algorithm solves the segmented least squares
problem in O(n3
) time and O(n2
) space.
Pf.
・Bottleneck = computing SSE eij for each i and j.
・O(n) to compute eij. ▪
Remark. Can be improved to O(n2
) time.
・For each i : precompute cumulative sums .
・Using cumulative sums, can compute eij in O(1) time.
30
aij =
n
!
k xkyk − (
!
k xk)(
!
k yk)
n
!
k x2
k − (
!
k xk)2
, bij =
!
k yk − aij
!
k xk
n
<latexit sha1_base64="JiXEyfCjefrho5PdKjL7JUVzDmM=">AAACyXicbVHdStxAFJ6krf/a1V72ZqgUFOySLLQqpbDgTS96YaFbhc0aTiYnOt3JJM6P7Dbkqi/iO/g0gg/Tya7W7uqBmfn4zu98JykF1yYIbj3/xctXC4tLyyura+sbr1ubWz91YRXDHitEoU4T0Ci4xJ7hRuBpqRDyROBJMjxq/CdXqDQv5A8zLnGQw7nkGWdgHBW3riGu+K+aRp/pl+aKMgWskjTSNo+HdBQPx+75QHceid0H7Dy79UzsWWcu9KxT79Ho0kJKk+caPVZyiQ+j/Et3xeu4tR20g4nRpyC8B9vd/Zu7LiHkON70tqK0YDZHaZgArfthUJpBBcpwJrBeiazGEtgQzrHvoIQc9aCaSFnT945JaVYod6ShE/b/jApyrcd54iJzMBd63teQz/n61mQHg4rL0hqUbNoos4KagjZ7oSlXyIwYOwBMcTcrZRfgNDJuezNdJrVLZDM/qUZWclakOMcKMzIKGhXDec2egl6nfdgOvzs1D8jUlshb8o7skJDsky75So5JjzBvwdvzPnqf/G++8kf+72mo793nvCEz5v/5CzSm3bw=</latexit>
<latexit sha1_base64="CRJSkf/k/PXSE8sZbaW7avsGjhU=">AAACyXicbVHdTtRAFJ5WBQTUBS69mUhMIMFNu4ksRk1IvOHCC0xcIdkuzen0FIadTuv8mF2bXvEiJj6CT0PgYZzugrgLJ5mZL9/5ne8kpeDaBMGl5z96/GRhcenp8srqs+cvWmvr33RhFcMeK0ShjhPQKLjEnuFG4HGpEPJE4FEy/NT4j36g0ryQX824xEEOp5JnnIFxVNz6BXHFz2savacfmyvKFLBK0kjbPB7SUTwcu+cN3bojtm+x82zXM7EnnbnQk069Q6PvFlKaPNTorpJLvB3lX7orXsetzaAdTIzeB+EN2Nzv/rnu/r76cBiveetRWjCbozRMgNb9MCjNoAJlOBNYL0dWYwlsCKfYd1BCjnpQTaSs6WvHpDQrlDvS0An7f0YFudbjPHGROZgzPe9ryId8fWuyvUHFZWkNSjZtlFlBTUGbvdCUK2RGjB0ApriblbIzcBoZt72ZLpPaJbKZn1QjKzkrUpxjhRkZBY2K4bxm90Gv037XDr84NffI1JbIS/KKbJGQdMk+OSCHpEeYt+DteG+9Xf+zr/yR/3Ma6ns3ORtkxvyLv+PP320=</latexit>
<latexit sha1_base64="CRJSkf/k/PXSE8sZbaW7avsGjhU=">AAACyXicbVHdTtRAFJ5WBQTUBS69mUhMIMFNu4ksRk1IvOHCC0xcIdkuzen0FIadTuv8mF2bXvEiJj6CT0PgYZzugrgLJ5mZL9/5ne8kpeDaBMGl5z96/GRhcenp8srqs+cvWmvr33RhFcMeK0ShjhPQKLjEnuFG4HGpEPJE4FEy/NT4j36g0ryQX824xEEOp5JnnIFxVNz6BXHFz2savacfmyvKFLBK0kjbPB7SUTwcu+cN3bojtm+x82zXM7EnnbnQk069Q6PvFlKaPNTorpJLvB3lX7orXsetzaAdTIzeB+EN2Nzv/rnu/r76cBiveetRWjCbozRMgNb9MCjNoAJlOBNYL0dWYwlsCKfYd1BCjnpQTaSs6WvHpDQrlDvS0An7f0YFudbjPHGROZgzPe9ryId8fWuyvUHFZWkNSjZtlFlBTUGbvdCUK2RGjB0ApriblbIzcBoZt72ZLpPaJbKZn1QjKzkrUpxjhRkZBY2K4bxm90Gv037XDr84NffI1JbIS/KKbJGQdMk+OSCHpEeYt+DteG+9Xf+zr/yR/3Ma6ns3ORtkxvyLv+PP320=</latexit>
<latexit sha1_base64="BChx1F3fNhGq6mUCFDX2bORLMoA=">AAACyXicbVFdb9MwFHUCjDG+uvHIi0WFtEmjSioBQwhpEi888DAkyiY1XXTj3GxeHSfY16glyhN/hL/Fv8HpOka7Xcn20bmfPjerlbQURX+C8M7dexv3Nx9sPXz0+MnT3vbON1s5I3AkKlWZkwwsKqlxRJIUntQGocwUHmfTj53/+AcaKyv9leY1Tko407KQAshTae83pI28aHnynn/orqQwIBrNE+vKdMpn6XTun1d895rYu8Les9euxJ4O10JPh+0+T747yHl2W6PrSj7xapR/6b54m/b60SBaGL8J4iXos6UdpdvBTpJXwpWoSSiwdhxHNU0aMCSFwnYrcRZrEFM4w7GHGkq0k2YhZctfeibnRWX80cQX7P8ZDZTWzsvMR5ZA53bd15G3+caOioNJI3XtCLW4bFQ4xani3V54Lg0KUnMPQBjpZ+XiHLxG5Le30mVRu0ax8pNm5rQUVY5rrKIZGehUjNc1uwlGw8G7Qfwl6h8eLOXcZM/ZC7bLYvaWHbJP7IiNmAg2gv3gdfAm/ByacBb+vAwNg2XOM7Zi4a+/kPPbdg==</latexit>
i
k=1
xk,
i
k=1
yk,
i
k=1
x2
k,
i
k=1
xkyk
<latexit sha1_base64="E9Bo6rLIFL0/cuHYqsa/2SHtfn0=">AAACh3icbVDLSgMxFE3Hd33VunQTLIILKTMiPhZCxY1LBatCH0Mmc6uhmcyY3EjL0L/zJ/wFt/oBpnUQWz0QOJxzT25yokwKg77/VvLm5hcWl5ZXyqtr6xubla3qnUmt5tDkqUz1Q8QMSKGgiQIlPGQaWBJJuI/6l2P//gW0Eam6xWEGnYQ9KtETnKGTwkq3bWwS5v3zYNQVdBD2D2j72bKYTunDH708O989/DfhnHEqrNT8uj8B/UuCgtRIgetwq1Rtxym3CSjkkhnTCvwMOznTKLiEUbltDWSM99kjtBxVLAHTySdFjOieU2LaS7U7CulE/Z3IWWLMMIncZMLwycx6Y/E/r2Wxd9rJhcosguLfi3pWUkzpuFUaCw0c5dARxrVwb6X8iWnG0XU/tWVydwZ86if5wCrB0xhmVIkD1GzkWgxmO/tLmof1s3pwc1RrnBZ1LpMdskv2SUBOSINckWvSJJy8knfyQT69sud7x14x65WKzDaZgnfxBVkmxzI=</latexit>
<latexit sha1_base64="E9Bo6rLIFL0/cuHYqsa/2SHtfn0=">AAACh3icbVDLSgMxFE3Hd33VunQTLIILKTMiPhZCxY1LBatCH0Mmc6uhmcyY3EjL0L/zJ/wFt/oBpnUQWz0QOJxzT25yokwKg77/VvLm5hcWl5ZXyqtr6xubla3qnUmt5tDkqUz1Q8QMSKGgiQIlPGQaWBJJuI/6l2P//gW0Eam6xWEGnYQ9KtETnKGTwkq3bWwS5v3zYNQVdBD2D2j72bKYTunDH708O989/DfhnHEqrNT8uj8B/UuCgtRIgetwq1Rtxym3CSjkkhnTCvwMOznTKLiEUbltDWSM99kjtBxVLAHTySdFjOieU2LaS7U7CulE/Z3IWWLMMIncZMLwycx6Y/E/r2Wxd9rJhcosguLfi3pWUkzpuFUaCw0c5dARxrVwb6X8iWnG0XU/tWVydwZ86if5wCrB0xhmVIkD1GzkWgxmO/tLmof1s3pwc1RrnBZ1LpMdskv2SUBOSINckWvSJJy8knfyQT69sud7x14x65WKzDaZgnfxBVkmxzI=</latexit>
<latexit sha1_base64="E9Bo6rLIFL0/cuHYqsa/2SHtfn0=">AAACh3icbVDLSgMxFE3Hd33VunQTLIILKTMiPhZCxY1LBatCH0Mmc6uhmcyY3EjL0L/zJ/wFt/oBpnUQWz0QOJxzT25yokwKg77/VvLm5hcWl5ZXyqtr6xubla3qnUmt5tDkqUz1Q8QMSKGgiQIlPGQaWBJJuI/6l2P//gW0Eam6xWEGnYQ9KtETnKGTwkq3bWwS5v3zYNQVdBD2D2j72bKYTunDH708O989/DfhnHEqrNT8uj8B/UuCgtRIgetwq1Rtxym3CSjkkhnTCvwMOznTKLiEUbltDWSM99kjtBxVLAHTySdFjOieU2LaS7U7CulE/Z3IWWLMMIncZMLwycx6Y/E/r2Wxd9rJhcosguLfi3pWUkzpuFUaCw0c5dARxrVwb6X8iWnG0XU/tWVydwZ86if5wCrB0xhmVIkD1GzkWgxmO/tLmof1s3pwc1RrnBZ1LpMdskv2SUBOSINckWvSJJy8knfyQT69sud7x14x65WKzDaZgnfxBVkmxzI=</latexit>
<latexit sha1_base64="E9Bo6rLIFL0/cuHYqsa/2SHtfn0=">AAACh3icbVDLSgMxFE3Hd33VunQTLIILKTMiPhZCxY1LBatCH0Mmc6uhmcyY3EjL0L/zJ/wFt/oBpnUQWz0QOJxzT25yokwKg77/VvLm5hcWl5ZXyqtr6xubla3qnUmt5tDkqUz1Q8QMSKGgiQIlPGQaWBJJuI/6l2P//gW0Eam6xWEGnYQ9KtETnKGTwkq3bWwS5v3zYNQVdBD2D2j72bKYTunDH708O989/DfhnHEqrNT8uj8B/UuCgtRIgetwq1Rtxym3CSjkkhnTCvwMOznTKLiEUbltDWSM99kjtBxVLAHTySdFjOieU2LaS7U7CulE/Z3IWWLMMIncZMLwycx6Y/E/r2Wxd9rJhcosguLfi3pWUkzpuFUaCw0c5dARxrVwb6X8iWnG0XU/tWVydwZ86if5wCrB0xhmVIkD1GzkWgxmO/tLmof1s3pwc1RrnBZ1LpMdskv2SUBOSINckWvSJJy8knfyQT69sud7x14x65WKzDaZgnfxBVkmxzI=</latexit>](https://image.slidesharecdn.com/06dynamicprogrammingi-240815151754-56ae93ab/85/06DynamicProgramming-in-algorithms-CSE-pdf-30-320.jpg)





![Knapsack problem: bottom-up dynamic programming
36
KNAPSACK(n, W, w1, …, wn, v1, …, vn )
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
FOR w = 0 TO W
M[0, w] ← 0.
FOR i = 1 TO n
FOR w = 0 TO W
IF (wi > w) M[i, w] ← M[i – 1, w].
ELSE M[i, w] ← max { M[i – 1, w], vi + M[i – 1, w – wi] }.
RETURN M[n, W].
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
previously computed values
OPT(i, w) =
0 B7 i = 0
OPT(i 1, w) B7 wi > w
max { OPT(i 1, w), vi + OPT(i 1, w wi) } Qi?2`rBb2
<latexit sha1_base64="yGc+dBk4QwRLdPr1J0EKEi2YjzI=">AAADBHicbVFNb9NAEF2brxK+0nLkMiICFZFGNkKlKCoq4sKNIDW0UjaK1puxs+p67e6um0RWzvwaTogr/wPxZ1i7OTgpI6309Gbem9mZKJfC2CD44/m3bt+5e2/nfuvBw0ePn7R3976ZrNAchzyTmT6PmEEpFA6tsBLPc40sjSSeRRefqvzZFWojMnVqlzmOU5YoEQvOrKMm7b9fBqf7ogvzV0D7x7TfohEmQpXceZpVi/YDeAnU4sJCCSKGFQg4hgAoHfUOMR27itrhIKw9tmrnEwEfYN6spilbAJUYW6Cl6wkNeRdot6KunOx1I3HgfKr5gGqRzJxw1WiU2RnquTDo+lHaoqim6+kn7U7QC+qAmyBcgw5Zx2Cy6+3RacaLFJXlkhkzCoPcjkumreAS3ToKgznjFyzBkYOKpWjGZX2FFbxwzBTiTLunLNRsU1Gy1JhlGrnKlNmZ2c5V5P9yo8LGR+NSqLywqPh1o7iQYDOoTgpToZFbuXSAcS3crMBnTDNu3eE3utTeOfKNn5SLQgmeTXGLlXZhNau2GG7v7CYYvum974Vf33ZOjtbr3CHPyHOyT0LyjpyQz2RAhoR7H73Ey71L/7v/w//p/7ou9b215inZCP/3P7Vj6Os=</latexit>
<latexit sha1_base64="yGc+dBk4QwRLdPr1J0EKEi2YjzI=">AAADBHicbVFNb9NAEF2brxK+0nLkMiICFZFGNkKlKCoq4sKNIDW0UjaK1puxs+p67e6um0RWzvwaTogr/wPxZ1i7OTgpI6309Gbem9mZKJfC2CD44/m3bt+5e2/nfuvBw0ePn7R3976ZrNAchzyTmT6PmEEpFA6tsBLPc40sjSSeRRefqvzZFWojMnVqlzmOU5YoEQvOrKMm7b9fBqf7ogvzV0D7x7TfohEmQpXceZpVi/YDeAnU4sJCCSKGFQg4hgAoHfUOMR27itrhIKw9tmrnEwEfYN6spilbAJUYW6Cl6wkNeRdot6KunOx1I3HgfKr5gGqRzJxw1WiU2RnquTDo+lHaoqim6+kn7U7QC+qAmyBcgw5Zx2Cy6+3RacaLFJXlkhkzCoPcjkumreAS3ToKgznjFyzBkYOKpWjGZX2FFbxwzBTiTLunLNRsU1Gy1JhlGrnKlNmZ2c5V5P9yo8LGR+NSqLywqPh1o7iQYDOoTgpToZFbuXSAcS3crMBnTDNu3eE3utTeOfKNn5SLQgmeTXGLlXZhNau2GG7v7CYYvum974Vf33ZOjtbr3CHPyHOyT0LyjpyQz2RAhoR7H73Ey71L/7v/w//p/7ou9b215inZCP/3P7Vj6Os=</latexit>
<latexit sha1_base64="yGc+dBk4QwRLdPr1J0EKEi2YjzI=">AAADBHicbVFNb9NAEF2brxK+0nLkMiICFZFGNkKlKCoq4sKNIDW0UjaK1puxs+p67e6um0RWzvwaTogr/wPxZ1i7OTgpI6309Gbem9mZKJfC2CD44/m3bt+5e2/nfuvBw0ePn7R3976ZrNAchzyTmT6PmEEpFA6tsBLPc40sjSSeRRefqvzZFWojMnVqlzmOU5YoEQvOrKMm7b9fBqf7ogvzV0D7x7TfohEmQpXceZpVi/YDeAnU4sJCCSKGFQg4hgAoHfUOMR27itrhIKw9tmrnEwEfYN6spilbAJUYW6Cl6wkNeRdot6KunOx1I3HgfKr5gGqRzJxw1WiU2RnquTDo+lHaoqim6+kn7U7QC+qAmyBcgw5Zx2Cy6+3RacaLFJXlkhkzCoPcjkumreAS3ToKgznjFyzBkYOKpWjGZX2FFbxwzBTiTLunLNRsU1Gy1JhlGrnKlNmZ2c5V5P9yo8LGR+NSqLywqPh1o7iQYDOoTgpToZFbuXSAcS3crMBnTDNu3eE3utTeOfKNn5SLQgmeTXGLlXZhNau2GG7v7CYYvum974Vf33ZOjtbr3CHPyHOyT0LyjpyQz2RAhoR7H73Ey71L/7v/w//p/7ou9b215inZCP/3P7Vj6Os=</latexit>
<latexit sha1_base64="yGc+dBk4QwRLdPr1J0EKEi2YjzI=">AAADBHicbVFNb9NAEF2brxK+0nLkMiICFZFGNkKlKCoq4sKNIDW0UjaK1puxs+p67e6um0RWzvwaTogr/wPxZ1i7OTgpI6309Gbem9mZKJfC2CD44/m3bt+5e2/nfuvBw0ePn7R3976ZrNAchzyTmT6PmEEpFA6tsBLPc40sjSSeRRefqvzZFWojMnVqlzmOU5YoEQvOrKMm7b9fBqf7ogvzV0D7x7TfohEmQpXceZpVi/YDeAnU4sJCCSKGFQg4hgAoHfUOMR27itrhIKw9tmrnEwEfYN6spilbAJUYW6Cl6wkNeRdot6KunOx1I3HgfKr5gGqRzJxw1WiU2RnquTDo+lHaoqim6+kn7U7QC+qAmyBcgw5Zx2Cy6+3RacaLFJXlkhkzCoPcjkumreAS3ToKgznjFyzBkYOKpWjGZX2FFbxwzBTiTLunLNRsU1Gy1JhlGrnKlNmZ2c5V5P9yo8LGR+NSqLywqPh1o7iQYDOoTgpToZFbuXSAcS3crMBnTDNu3eE3utTeOfKNn5SLQgmeTXGLlXZhNau2GG7v7CYYvum974Vf33ZOjtbr3CHPyHOyT0LyjpyQz2RAhoR7H73Ey71L/7v/w//p/7ou9b215inZCP/3P7Vj6Os=</latexit>](https://image.slidesharecdn.com/06dynamicprogrammingi-240815151754-56ae93ab/85/06DynamicProgramming-in-algorithms-CSE-pdf-36-320.jpg)

![Knapsack problem: running time
Theorem. The DP algorithm solves the knapsack problem with n items
and maximum weight W in Θ(n W) time and Θ(n W) space.
Pf.
・Takes O(1) time per table entry.
・There are Θ(n W) table entries.
・After computing optimal values, can trace back to find solution:
OPT(i, w) takes item i iff M [i, w] > M [i – 1, w]. ▪
Remarks.
・Algorithm depends critically on assumption that weights are integral.
・Assumption that values are integral was not used.
38
weights are integers
between 1 and W](https://image.slidesharecdn.com/06dynamicprogrammingi-240815151754-56ae93ab/85/06DynamicProgramming-in-algorithms-CSE-pdf-38-320.jpg)





![Secondary structure. A set of pairs S = { (bi, bj) } that satisfy:
・[Watson–Crick] S is a matching and each pair in S is a Watson–Crick
complement: A–U, U–A, C–G, or G–C.
RNA secondary structure
44
A C G U G G C C A U
S is not a secondary structure
(C-A is not a valid Watson-Crick pair)
B = ACGUGGCCCAU
S = { (b1, b10), (b2, b9), (b3, b8) }
base pair
in secondary structure
C
G G
C
A
G
C
U
U A](https://image.slidesharecdn.com/06dynamicprogrammingi-240815151754-56ae93ab/85/06DynamicProgramming-in-algorithms-CSE-pdf-44-320.jpg)
![Secondary structure. A set of pairs S = { (bi, bj) } that satisfy:
・[Watson–Crick] S is a matching and each pair in S is a Watson–Crick
complement: A–U, U–A, C–G, or G–C.
・[No sharp turns] The ends of each pair are separated by at least 4
intervening bases. If (bi, bj) ∈ S, then i < j – 4.
RNA secondary structure
45
G G
C
A
G
U
U A
G
A U G G G C A U
S is not a secondary structure
(≤4 intervening bases between G and C)
G
B = AUGGGGCAU
S = { (b1, b9), (b2, b8), (b3, b7) }](https://image.slidesharecdn.com/06dynamicprogrammingi-240815151754-56ae93ab/85/06DynamicProgramming-in-algorithms-CSE-pdf-45-320.jpg)
![Secondary structure. A set of pairs S = { (bi, bj) } that satisfy:
・[Watson–Crick] S is a matching and each pair in S is a Watson–Crick
complement: A–U, U–A, C–G, or G–C.
・[No sharp turns] The ends of each pair are separated by at least 4
intervening bases. If (bi, bj) ∈ S, then i < j – 4.
・[Non-crossing] If (bi, bj) and (bk, bℓ) are two pairs in S, then we cannot
have i < k < j < ℓ.
RNA secondary structure
46
A G U U G G C C A U
S is not a secondary structure
(G-C and U-A cross)
C
G G
C
A
U
G
U
U A
B = ACUUGGCCAU
S = { (b1, b10), (b2, b8), (b3, b9) }](https://image.slidesharecdn.com/06dynamicprogrammingi-240815151754-56ae93ab/85/06DynamicProgramming-in-algorithms-CSE-pdf-46-320.jpg)
![Secondary structure. A set of pairs S = { (bi, bj) } that satisfy:
・[Watson–Crick] S is a matching and each pair in S is a Watson–Crick
complement: A–U, U–A, C–G, or G–C.
・[No sharp turns] The ends of each pair are separated by at least 4
intervening bases. If (bi, bj) ∈ S, then i < j – 4.
・[Non-crossing] If (bi, bj) and (bk, bℓ) are two pairs in S, then we cannot
have i < k < j < ℓ.
RNA secondary structure
47
A U G U G G C C A U
S is a secondary structure
(with 3 base pairs)
C
G G
C
A
G
U
U
U A
B = AUGUGGCCAU
S = { (b1, b10), (b2, b9), (b3, b8) }](https://image.slidesharecdn.com/06dynamicprogrammingi-240815151754-56ae93ab/85/06DynamicProgramming-in-algorithms-CSE-pdf-47-320.jpg)
![RNA secondary structure
Secondary structure. A set of pairs S = { (bi, bj) } that satisfy:
・[Watson–Crick] S is a matching and each pair in S is a Watson–Crick
complement: A–U, U–A, C–G, or G–C.
・[No sharp turns] The ends of each pair are separated by at least 4
intervening bases. If (bi, bj) ∈ S, then i < j – 4.
・[Non-crossing] If (bi, bj) and (bk, bℓ) are two pairs in S, then we cannot
have i < k < j < ℓ.
Free-energy hypothesis. RNA molecule will form the secondary structure
with the minimum total free energy.
Goal. Given an RNA molecule B = b1b2…bn, find a secondary structure S
that maximizes the number of base pairs.
approximate by number of base pairs
(more base pairs ⇒ lower free energy)
48](https://image.slidesharecdn.com/06dynamicprogrammingi-240815151754-56ae93ab/85/06DynamicProgramming-in-algorithms-CSE-pdf-48-320.jpg)





![Bottom-up dynamic programming over intervals
Q. In which order to solve the subproblems?
A. Do shortest intervals first—increasing order of ⎜j − i⎟.
Theorem. The DP algorithm solves the RNA secondary structure problem in
O(n3
) time and O(n2
) space.
54
6 7 8 9 10
4 0 0 0
3 0 0
2 0
1
i
j
order in which to solve subproblems
RNA-SECONDARY-STRUCTURE(n, b1, …, bn )
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
FOR k = 5 TO n – 1
FOR i = 1 TO n – k
j ← i + k.
Compute M[i, j] using formula.
RETURN M[1, n].
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
all needed values
are already computed](https://image.slidesharecdn.com/06dynamicprogrammingi-240815151754-56ae93ab/85/06DynamicProgramming-in-algorithms-CSE-pdf-54-320.jpg)
