A Comprehensive Introduction To Objectoriented Programming With Java C Thomas Wu
- 1. A Comprehensive Introduction To Objectoriented Programming With Java C Thomas Wu download https://ebookbell.com/product/a-comprehensive-introduction-to- objectoriented-programming-with-java-c-thomas-wu-2404444 Explore and download more ebooks at ebookbell.com
- 2. Here are some recommended products that we believe you will be interested in. You can click the link to download. A Comprehensive Introduction To Subriemannian Geometry Andrei Agrachev https://ebookbell.com/product/a-comprehensive-introduction-to- subriemannian-geometry-andrei-agrachev-10664690 A Comprehensive Introduction To The Mari Language 21 Timothy Riese https://ebookbell.com/product/a-comprehensive-introduction-to-the- mari-language-21-timothy-riese-4164410 A Comprehensive Introduction To Computer Networks Winter Christopher https://ebookbell.com/product/a-comprehensive-introduction-to- computer-networks-winter-christopher-11712710 Ir Playbook A Comprehensive Introduction To Interventional Radiology May 3 20243031525450springer Nicole A Keefe https://ebookbell.com/product/ir-playbook-a-comprehensive- introduction-to-interventional-radiology-may-3-20243031525450springer- nicole-a-keefe-57010586
- 3. Ir Playbook A Comprehensive Introduction To Interventional Radiology 1st Nicole A Keefe Et Al Eds https://ebookbell.com/product/ir-playbook-a-comprehensive- introduction-to-interventional-radiology-1st-nicole-a-keefe-et-al- eds-7108540 Terrorism And Counterterrorism A Comprehensive Introduction To Actors And Actions Henry Prunckun Troy Whitford https://ebookbell.com/product/terrorism-and-counterterrorism-a- comprehensive-introduction-to-actors-and-actions-henry-prunckun-troy- whitford-51894728 Engineering Your Future A Comprehensive Introduction To Engineering 9th Edition 9th Edition Oakes https://ebookbell.com/product/engineering-your-future-a-comprehensive- introduction-to-engineering-9th-edition-9th-edition-oakes-38624128 Ultrafast Lasers A Comprehensive Introduction To Fundamental Principles With Practical Applications 1st Ed 2021 Keller https://ebookbell.com/product/ultrafast-lasers-a-comprehensive- introduction-to-fundamental-principles-with-practical- applications-1st-ed-2021-keller-38649482 Hermeneutical Spiral A Comprehensive Introduction To Biblical Interpretation Grant R Osborne https://ebookbell.com/product/hermeneutical-spiral-a-comprehensive- introduction-to-biblical-interpretation-grant-r-osborne-7244114
- 5. A Comprehensive Introduction to Object-Oriented Programming with JavaTM C.Thomas Wu Naval Postgraduate School wu23399_fm.qxd 1/10/07 11:53 Page i
- 6. A COMPREHENSIVE INTRODUCTION TO OBJECT-ORIENTED PROGRAMMING WITH JAVA Published by McGraw-Hill, a business unit of The McGraw-Hill Companies, Inc., 1221 Avenue of the Americas, New York, NY 10020. Copyright © 2008 by The McGraw-Hill Companies, Inc. All rights reserved. No part of this publication may be reproduced or distributed in any form or by any means, or stored in a database or retrieval system, without the prior written consent of The McGraw-Hill Companies, Inc., including, but not limited to, in any network or other electronic storage or transmission, or broadcast for distance learning. Some ancillaries, including electronic and print components, may not be available to customers outside the United States. This book is printed on acid-free paper. 1 2 3 4 5 6 7 8 9 0 DOC/DOC 0 9 8 7 ISBN 978–0–07–352339–2 MHID 0–07–352339–9 Publisher: Alan R. Apt Executive Marketing Manager: Michael Weitz Senior Project Manager: Sheila M. Frank Lead Production Supervisor: Sandy Ludovissy Associate Media Producer: Christina Nelson Designer: Rick D. Noel Cover Designer: Elise Lansdon (USE) Cover Image: breaking wave on foaming ocean surface, ®Ron Dahlquist/Getty Images Compositor: ICC Macmillan Inc. Typeface: 10.5/12 Times Roman Printer: R. R. Donnelley Crawfordsville, IN Library of Congress Cataloging-in-Publication Data Wu, C. Thomas. A comprehensive introduction to object-oriented programming with Java / C. Thomas Wu. – 1st ed. p. cm. ISBN 978–0–07–352339–2 — ISBN 0–07–352339–9 1. Object-oriented programming (Computer science) 2. Java (Computer program language) I. Title. QA76.64.W77 2008 005.117–dc22 2006048064 www.mhhe.com wu23399_fm.qxd 1/10/07 11:53 Page ii
- 7. To my family wu23399_fm.qxd 1/10/07 11:53 Page iii
- 8. wu23399_fm.qxd 1/10/07 11:53 Page iv
- 9. v Preface xiii Key Differences from the Standard Edition xiii Book Organization xiv Hallmark Features of the Text xviii 0 Introduction to Computers and Programming Languages 1 0.1 A History of Computers 2 0.2 Computer Architecture 4 0.3 Programming Languages 11 0.4 Java 12 1 Introduction to Object-Oriented Programming and Software Development 15 1.1 Classes and Objects 16 1.2 Messages and Methods 18 1.3 Class and Instance Data Values 20 1.4 Inheritance 23 1.5 Software Engineering and Software Life Cycle 24 C o n t e n t s wu23399_fm.qxd 1/10/07 11:53 Page v
- 10. 2 Getting Started with Java 29 2.1 The First Java Program 30 2.2 Program Components 39 2.3 Edit-Compile-Run Cycle 49 2.4 Sample Java Standard Classes 52 2.5 Sample Development 67 3 Numerical Data 81 3.1 Variables 82 3.2 Arithmetic Expressions 90 3.3 Constants 95 3.4 Displaying Numerical Values 97 3.5 Getting Numerical Input 103 3.6 The Math Class 109 3.7 Random Number Generation 113 3.8 The GregorianCalendar Class 115 3.9 Sample Development 120 3.10 Numerical Representation (Optional) 131 4 Defining Your Own Classes—Part 1 145 4.1 First Example:Defining and Using a Class 146 4.2 Second Example:Defining and Using Multiple Classes 156 4.3 Matching Arguments and Parameters 160 4.4 Passing Objects to a Method 162 4.5 Constructors 167 4.6 Information Hiding and Visibility Modifiers 172 4.7 Class Constants 175 4.8 Local Variables 183 4.9 Calling Methods of the Same Class 185 4.10 Changing Any Class to a Main Class 189 4.11 Sample Development 190 vi Contents wu23399_fm.qxd 1/10/07 11:53 Page vi
- 11. Contents vii 5 Selection Statements 213 5.1 The if Statement 214 5.2 Nested if Statements 225 5.3 Boolean Expressions and Variables 231 5.4 Comparing Objects 239 5.5 The switch Statement 244 5.6 Drawing Graphics 248 5.7 Enumerated Constants 258 5.8 Sample Development 264 6 Repetition Statements 295 6.1 The while Statement 296 6.2 Pitfalls in Writing Repetition Statements 305 6.3 The do–while Statement 311 6.4 Loop-and-a-Half Repetition Control 315 6.5 The for Statement 319 6.6 Nested for Statements 324 6.7 Formatting Output 326 6.8 Loan Tables 331 6.9 Estimating the Execution Time 334 6.10 Recursive Methods (Optional) 338 6.11 Sample Development 343 7 Defining Your Own Classes—Part 2 365 7.1 Returning an Object from a Method 366 7.2 The Reserved Word this 370 7.3 Overloaded Methods and Constructors 378 7.4 Class Variables and Methods 383 wu23399_fm.qxd 1/10/07 11:53 Page vii
- 12. viii Contents 7.5 Call-by-Value Parameter Passing 387 7.6 Organizing Classes into a Package 394 7.7 Using Javadoc Comments for Class Documentation 395 7.8 The Complete Fraction Class 400 7.9 Sample Development 410 8 Exceptions and Assertions 437 8.1 Catching Exceptions 438 8.2 Throwing Exceptions and Multiple catch Blocks 445 8.3 Propagating Exceptions 450 8.4 Types of Exceptions 458 8.5 Programmer-Defined Exceptions 461 8.6 Assertions 463 8.7 Sample Development 469 9 Characters and Strings 487 9.1 Characters 488 9.2 Strings 491 9.3 Pattern Matching and Regular Expression 502 9.4 The Pattern and Matcher Classes 509 9.5 Comparing Strings 513 9.6 StringBuffer and StringBuilder 515 9.7 Sample Development 521 10 Arrays and Collections 543 10.1 Array Basics 544 10.2 Arrays of Objects 555 10.3 The For-Each Loop 565 wu23399_fm.qxd 1/10/07 11:53 Page viii
- 13. Contents ix 10.4 Passing Arrays to Methods 569 10.5 Two-Dimensional Arrays 576 10.6 Lists and Maps 583 10.7 Sample Development 596 11 Sorting and Searching 619 11.1 Searching 620 11.2 Sorting 624 11.3 Heapsort 632 11.4 Sample Development 645 12 File Input and Output 669 12.1 File and JFileChooser Objects 670 12.2 Low-Level File I/O 679 12.3 High-Level File I/O 684 12.4 Object I/O 693 12.5 Sample Development 700 13 Inheritance and Polymorphism 713 13.1 A Simple Example 714 13.2 Defining Classes with Inheritance 717 13.3 Using Classes Effectively with Polymorphism 721 13.4 Inheritance and Member Accessibility 724 13.5 Inheritance and Constructors 729 13.6 Abstract Superclasses and Abstract Methods 733 13.7 Inheritance versus Interface 738 13.8 Sample Development 739 wu23399_fm.qxd 1/12/07 13:15 Page ix
- 14. x Contents 14 GUI and Event-Driven Programming 765 14.1 Simple GUI I/O with JOptionPane 768 14.2 Customizing Frame Windows 771 14.3 GUI Programming Basics 777 14.4 Text-Related GUI Components 787 14.5 Layout Managers 798 14.6 Effective Use of Nested Panels 808 14.7 Other GUI Components 817 14.8 Menus 835 14.9 Handling Mouse Events 839 15 Recursive Algorithms 859 15.1 Basic Elements of Recursion 860 15.2 Directory Listing 861 15.3 Anagram 863 15.4 Towers of Hanoi 866 15.5 Quicksort 868 15.6 When Not to Use Recursion 873 16 Memory Allocation Schemes and Linked Data Structures 879 16.1 Contiguous Memory Allocation Scheme 881 16.2 Noncontiguous Memory Allocation Scheme 886 16.3 Manipulating Linked Lists 890 16.4 Linked Lists of Objects 903 16.5 Sample Development 908 wu23399_fm.qxd 1/10/07 11:53 Page x
- 15. Contents xi 17 Generics and Type Safety 945 17.1 Generic Classes 946 17.2 Generics and Collections 961 17.3 Generics,Inheritance,and Java Interface 969 17.4 Additional Topics and Pitfalls 974 18 List ADT 981 18.1 The List ADT 982 18.2 The List Interface 988 18.3 The Array Implementation of the List ADT 992 18.4 The Linked-List Implementation of the List ADT 1001 18.5 The Linked Implementation with the Head Node 1018 18.6 The Iterator Design Pattern 1022 18.7 Sample Development 1027 19 Stack ADT 1035 19.1 The Stack ADT 1036 19.2 The Stack Interface 1040 19.3 The Array Implementation 1042 19.4 The Linked-List Implementation 1047 19.5 Implementation Using NPSList 1052 19.6 Sample Applications:Matching HTML Tags 1053 19.7 Sample Applications:Solving a Maze with Backtracking 1060 wu23399_fm.qxd 1/10/07 11:53 Page xi
- 16. xii Contents 20 Queue ADT 1069 20.1 The Queue ADT 1070 20.2 The Queue Interface 1073 20.3 The Array Implementation 1075 20.4 The Linked-List Implementation 1082 20.5 Implementation Using NPSList 1088 20.6 Priority Queue 1089 Appendix A 1099 Appendix B 1107 Appendix C 1133 Appendix D 1155 Index 1163 wu23399_fm.qxd 1/10/07 11:53 Page xii
- 17. xiii P r e f a c e This book is an in-depth introduction to object-oriented programming using the Java programming language. In addition to covering traditional topics for a CS1 course, some of the more advanced topics such as recursion and linked lists are in- cluded to provide a comprehensive coverage of beginning to intermediate-level ma- terials. There are more materials in the book than what are normally covered in a typical CS1 course. An instructor may want to teach some of the chapters on data structures in an advanced CS1 course. Topics covered in Chapters 16 to 20 are also suitable for use in a CS2 course. Key Differences from the Standard Edition This comprehensive edition is based on An Introduction to Object-Oriented Pro- gramming with Java, Fourth Edition. The key differences between this comprehen- sive version and the fourth edition standard version are as follows: 1. Data Structures Chapters. Chapter 16 covers topics on managing linked nodes. Using this as the foundation, Chapters 18 through 20 present three ab- stract data types (ADTs) List, Stack, and Queue, respectively. For all three ADTs, both array-based and linked-list implementations are shown, and their relative advantages and disadvantages are discussed. 2. More Discussion on Java 5.0 Features. Many of the new Java 5.0 features are explained and used in the sample programs. They include the enumerator type, the for-each loop construct, auto boxing and unboxing, and the generics. One complete chapter (Chapter 17) is dedicated to the generics. 3. Exclusive Use of Console Input and Output. All the GUI related topics, including the JOptionPane class, are moved to Chapter 14. Sample programs before Chapter 14 use the standard console input (Scanner) and output (System.out). Those who want to use JOptionPane for simple input and output can do so easily by covering Section 14.1 before Chapter 3. wu23399_fm.qxd 1/10/07 11:53 Page xiii
- 18. xiv Preface Book Organization There are 21 chapters in this book, numbered from 0 to 20. The first 11 chapters cover the core topics that provide the fundamentals of programming. Chapters 11 to 15 cover intermediate-level topics such as sorting, searching, recursion, inheritance, polymorphism, and file I/O. And Chapters 16 to 20 cover topics related to data structures. There are more than enough topics for one semester. After the first 11 chapters (Ch 0 to Ch 10), instructors can mix and match materials from Chapters 11 to 20 to suit their needs. We first show the dependency relationships among the chapters and then provide a brief summary of each chapter. Chapter Dependency For the most part, chapters should be read in sequence, but some variations are possible, especially with the optional chapters. Here’s a simplified dependency graph: 0 1 2 3 4 5 6 7 8 9 10 15 14* 13 12 11 18 19 20 17 16 *Note: Some examples use arrays, but the use of arrays is not an integral part of the examples. These examples can be modified to those that do not use arrays. Many topics from the early part of the chapter can be introduced as early as after Chapter 2. wu23399_fm.qxd 1/10/07 11:53 Page xiv
- 19. Preface xv Brief Chapter Summary Here is a short description of each chapter: • Chapter 0 is an optional chapter. We provide background information on computers and programming languages. This chapter can be skipped or as- signed as an outside reading if you wish to start with object-oriented pro- gramming concepts. • Chapter 1 provides a conceptual foundation of object-oriented programming. We describe the key components of object-oriented programming and illus- trate each concept with a diagrammatic notation using UML. • Chapter 2 covers the basics of Java programming and the process of editing, compiling, and running a program. From the first sample program presented in this chapter, we emphasize object-orientation. We will introduce the standard classes String, Date, and SimpleDateFormat so we can reinforce the notion of object declaration, creation, and usage. Moreover, by using these standard classes, students can immediately start writing practical programs.We describe and illustrate console input with System.in and the new Scanner class and output with System.out. • Chapter 3 introduces variables, constants, and expressions for manipulating numerical data. We explain the standard Math class from java.lang and introduce more standard classes (GregorianCalendar and DecimalFormat) to continually reinforce the notion of object-orientation. We describe additional methods of the Scanner class to input numerical values. Random number generation is introduced in this chapter. The optional section explains how the numerical values are represented in memory space. • Chapter 4 teaches the basics of creating programmer-defined classes. We keep the chapter accessible by introducting only the fundamentals with illus- trative examples. The key topics covered in this chapter are constructors, vis- ibility modifiers (public and private), local variables, and passing data to methods. We provide easy-to-grasp illustrations that capture the essence of the topics so the students will have a clear understanding of them. • Chapter 5 explains the selection statements if and switch. We cover boolean expressions and nested-if statements. We explain how objects are compared by using equivalence (==) and equality (the equals and compareTo methods). We use the String and the programmer-defined Fraction classes to make the distinction between the equivalence and equality clear. Drawing 2-D graphics is introduced, and a screensaver sample development program is developed. We describe the new Java 5.0 feature called enumerated type in this chapter. • Chapter 6 explains the repetition statements while, do–while, and for. Pitfalls in writing repetition statements are explained. One of the pitfalls to avoid is the use of float or double for the data type of a counter variable. We illustrate this pitfall by showing a code that will result in infinite loop. Finding the great- est common divisor of two integers is used as an example of a nontrivial loop statement. We show the difference between the straightforward (brute-force) wu23399_fm.qxd 1/10/07 11:54 Page xv
- 20. xvi Preface and the clever (Euclid’s) solutions. We introduce the Formatter class (new to Java 5.0) and show how the output can be aligned nicely. The optional last sec- tion of the chapter introduces recursion as another technique for repetition. The recursive version of a method that finds the greatest common divisor of two integers is given. • Chapter 7 is the second part of creating programmer-defined classes. We introduce new topics related to the creation of programmer-defined classes and also repeat some of the topics covered in Chapter 4 in more depth. The key topics covered in this chapter are method overloading, the reserved word this, class methods and variables, returning an object from a method, and pass-by-value parameter passing. As in Chapter 4, we provide many lucid illustrations to make these topics accessible to beginners. We use the Fraction class to illustrate many of these topics, such as the use of this and class methods. The complete definition of the Fraction class is presented in this chapter. • Chapter 8 teaches exception handling and assertions. The focus of this chap- ter is the construction of reliable programs. We provide a detailed coverage of exception handling in this chapter. We introduce an assertion and show how it can be used to improve the reliability of finished products by catching logical errors early in the development. • Chapter 9 covers nonnumerical data types: characters and strings. Both the String and StringBuffer classes are explained in the chapter. Another string class named StringBuilder (new to Java 5.) is briefly explained in this chapter. An important application of string processing is pattern matching. We describe pattern matching and regular expression in this chapter. We introduce the Pattern and Matcher classes and show how they are used in pattern matching. • Chapter 10 teaches arrays. We cover arrays of primitive data types and of ob- jects. An array is a reference data type in Java, and we show how arrays are passed to methods. We describe how to process two-dimensional arrays and explain that a two-dimensional array is really an array of arrays in Java. Lists and maps are introduced as a more general and flexible way to maintain a col- lection of data. The use of ArrayList and HashMap classes from the java.util package is shown in the sample programs. Also, we show how the WordList helper class used in Chapter 9 sample development program is implemented with another map class called TreeMap. • Chapter 11 presents searching and sorting algorithms. Both N2 and Nlog2N sorting algorithms are covered. The mathematical analysis of searching and sorting algorithms can be omitted depending on the students’ background. • Chapter 12 explains the file I/O. Standard classes such as File and JFile- Chooser are explained. We cover all types of file I/O, from a low-level byte I/O to a high-level object I/O. We show how the file I/O techniques are used to implement the helper classes—Dorm and FileManager—in Chapter 8 and 9 sample development programs. The use of the Scanner class for inputting data from a textfile is also illustrated in this chapter. wu23399_fm.qxd 1/10/07 11:54 Page xvi
- 21. Preface xvii • Chapter 13 discusses inheritance and polymorphism and how to use them ef- fectively in program design. The effect of inheritance for member accessibil- ity and constructors is explained. We also explain the purpose of abstract classes and abstract methods. • Chapter 14 covers GUI and event-driven programming. Only the Swing- based GUI components are covered in this chapter. We show how to use the JOptionPane class for a very simple GUI-based input and output. GUI com- ponents introduced in this chapter include JButton, JLabel, ImageIcon, JTextField, JTextArea, and menu-related classes. We describe the effective use of nested panels and layout managers. Handling of mouse events is described and illustrated in the sample programs. Those who do not teach GUI can skip this chapter altogether. Those who teach GUI can introduce the beginning part of the chapter as early as after Chapter 2. • Chapter 15 covers recursion. Because we want to show the examples where the use of recursion really shines, we did not include any recursive algorithm (other than those used for explanation purposes) that really should be written nonrecursively. • Chapter 16 covers contiguous and noncontiguous memory allocation schemes and introduces the concept of linked lists. Ample examples are provided to illustrate the manipulation of linked lists of primitive data types and linked lists of objects. This chapter lays the necessary foundation for the students to learn different techniques for implementing the abstract data types covered in Chapters 18 through 20. • Chapter 17 covers new Java 5.0 generics in detail. The chapter describes how generic classes are defined and how the type safety is supported by generics. A concrete example of using generics is shown by defining a simple linked list with generic nodes. • Chapter 18 introduces the concept of abstract data types (ADT) and covers the List ADT. Key features of the List ADT are explained and two implemen- tations using an array and a linked list are shown. The iterator pattern to tra- verse the elements in the List ADT is introduced. • Chapter 19 covers the Stack ADT. Key features of the Stack ADT are ex- plained and two implementations using an array and a linked list are shown. Sample applications that use stacks are described. • Chapter 20 covers the Queue ADT. Key features of the Stack ADT are ex- plained and two implementations using an array and a linked list are shown. A special type of queue called a priority queue is also intoduced in this chapter. wu23399_fm.qxd 1/10/07 11:54 Page xvii
- 22. xviii Preface Development Exercises give students an opportunity to practice incremental development. Hallmark Features of the Text Problem Solving Printing the Initials Now that we have acquired a basic understanding of Java application programs, let’s write a new application.We will go through the design,coding,and testing phases of the software life cycle to illustrate the development process. Since the program we develop here is very simple,we can write it without really going through the phases.However,it is extremely important for you to get into a habit of developing a program by following the software life cycle stages. Small programs can be developed in a haphazard manner, but not large programs.We will teach you the development process with small programs first, so you will be ready to use it to create large programs later. We will develop this program by using an incremental development technique, which will develop the program in small incremental steps. We start out with a bare- bones program and gradually build up the program by adding more and more code to it. At each incremental step, we design, code, and test the program before moving on to the next step. This methodical development of a program allows us to focus our at- tention on a single task at each step, and this reduces the chance of introducing errors into the program. Problem Statement We start our development with a problem statement. The problem statement for our sample programs will be short,ranging from a sentence to a paragraph,but the problem statement for complex and advanced applications may contain many pages. Here’s the problem statement for this sample development exercise: Write an application that asks for the user’s first, middle, and last names and replies with the user’s initials. Overall Plan Our first task is to map out the overall plan for development.We will identify classes nec- essary for the program and the steps we will follow to implement the program.We begin with the outline of program logic.For a simple program such as this one,it is kind of obvi- ous; but to practice the incremental development, let’s put down the outline of program flow explicitly.We can express the program flow as having three tasks: 1. Get the user’s first,middle,and last names. 2. Extract the initials to formulate the monogram. 3. Output the monogram. Having identified the three major tasks of the program, we will now identify the classes we can use to implement the three tasks. First, we need an object to handle the input. At this point, we have learned about only the Scanner class, so we will use it here. Second, we need an object to display the result. Again, we will use System.out, as it is the only one we know at this point for displaying a string value. For the string Sample Development 2.5 Sample Development program tasks Sample Development Programs Most chapters include a sample development section that describes the process of incremental development. Development Exercises For the following exercises, use the incremental development methodology to implement the program. For each exercise, identify the program tasks, create a design document with class descriptions, and draw the program diagram. Map out the development steps at the start. Present any design alternatives and justify your selection. Be sure to perform adequate testing at the end of each development step. 8. In the sample development, we developed the user module of the keyless entry system. For this exercise, implement the administrative module that allows the system administrator to add and delete Resident objects and modify information on existing Resident objects. The module will also allow the user to open a list from a file and save the list to a file. Is it proper to implement the administrative module by using one class? Wouldn’t it be a better design if we used multiple classes with each class doing a single, well-defined task? 9. Write an application that maintains the membership lists of five social clubs in a dormitory. The five social clubs are the Computer Science Club, Biology Club, Billiard Club, No Sleep Club, and Wine Tasting Club. Use the Dorm wu23399_fm.qxd 1/10/07 11:54 Page xviii
- 23. Preface xix Object-Oriented Approach We take the object-first approach to teaching object-oriented programming with emphasis on proper object-oriented design.The concept of objects is clearly illustrated from the very first sample program. /* Chapter 2 Sample Program: Displaying a Window File: Ch2Sample1.java */ import javax.swing.*; class Ch2Sample1 { public static void main(String[] args) { JFrame myWindow; myWindow = new JFrame(); myWindow.setSize(300, 200); myWindow.setTitle(My First Java Program); myWindow.setVisible(true); } } Dorm Door Resident User module Dorm Resident A helper class provided to us A class we implement One or more classes we implement Administrative module Figure 8.8 Program diagrams for the user and administrative modules.Notice the same Dorm and Resident classes are used in both programs.User and administrative modules will include one or more classes (at least one is programmer-defined). Good practices on object- oriented design are discussed throughout the book and illustrated through numerous sample programs. wu23399_fm.qxd 1/10/07 11:55 Page xix
- 24. xx Preface Illustrative Diagrams Illustrative diagrams are used to explain all key concepts of programming such as the difference between object declaration and creation,the distinction between the primitive data type and the reference data type,the call-by-value parameter passing,inheritance,and many others. Numerical Data Object number1 = 237; number2 = number1; int number1, number2; alan = new Professor(); turing = alan; Professor alan, turing; number2 number1 turing alan number2 number1 turing alan number1 = 237; int number1, number2; alan = new Professor(); Professor alan, turing; number2 = number1; turing = alan; :Professor :Professor number2 number1 turing alan number1 = 237; int number1, number2; alan = new Professor(); Professor alan, turing; number2 = number1; turing = alan; 237 237 237 Figure 3.3 An effect of assigning the content of one variable to another. Figure 18.2 Sample version 2 add operations on myList. Before After Before After “cat” “gnu” “ape” “dog” “bee” 0 1 2 3 4 “cat” 0 “ape” 1 “dog” 2 “bee” 3 add(1, “gnu”) throws index-out-of-bounds-exception add(5, “gnu”) myList “cat” 0 “ape” 1 “dog” 2 “bee” 3 myList myList myList “cat” 0 “ape” 1 “dog” 2 “bee” 3 No structural change to the list Lucid diagrams are used effectively to explain data structures and abstract data types. wu23399_fm.qxd 1/10/07 11:55 Page xx
- 25. Preface xxi Student Pedagogy Always define a constructor and initialize data members fully in the constructor so an object will be created in a valid state. It is not necessary to create an object for every variable we use. Many novice pro- grammers often make this mistake.For example,we write Fraction f1, f2; f1 = new Fraction(24, 36); f2 = f1.simplify( ); We didn’t write Fraction f1, f2; f1 = new Fraction(24, 36); f2 = new Fraction(1, 1); //not necessary f2 = f1.simplify( ); because it is not necessary.The simplify method returns a Fraction object, and in the calling program, all we need is a name we can use to refer to this returned Fraction object.Don’t forget that the object name (variable) and the actual object instance are two separate things. We can turn our simulation program into a real one by replacing the Door class with a class that actually controls the door. Java provides a mechanism called Java Native Interface (JNI) which can be used to embed a link to a low- level device driver code, so calling the open method actually unlocks the door. 1. What will be displayed on the console window when the following code is executed and the user enters abc123 and 14? Scanner scanner = new Scanner(System.in); try { int num1 = scanner.nextInt(); System.out.println(Input 1 accepted); int num2 = scanner.nextInt(); System.out.println(Input 2 accepted); } catch (InputMismatchException e) { System.out.println(Invalid Entry); } List the catch blocks in the order of specialized to more general exception classes. At most one catch block is executed,and all other catch blocks are ignored. Design Guidelines provide tips on good program design. Things to Remember boxes provide tips for students to remember key concepts. Tips,Hints,and Pitfalls provide important points for which to watch out. You Might Want to Know boxes give students interesting bits of information. Quick Check exercises at the end of the sections allow students to test their comprehension of topics. wu23399_fm.qxd 1/10/07 11:55 Page xxi
- 26. xxii Preface Supplements for Instructors and Students On-Line Learning Center is located at www.mhhe.com/wu For Instructors • Complete set of PowerPoints, including lecture notes and figures. • Complete solutions for the exercises • Example Bank—Additional examples, which are searchable by topic, are provided online in a “bank” for instructors. • Homework Manager/Test Bank—Conceptual review questions are stored in this electronic question bank and can be assigned as exam questions or home- work. • Online labs which accompany this text, can be used in a closed lab, open lab, or for assigned programming projects. wu23399_fm.qxd 1/10/07 11:55 Page xxii
- 27. Preface xxiii For Students • Compiler How Tos provide tutorials on how to get up and running on the most popular compilers to aid students in using IDEs. • Interactive Quizzes allow students to test what they learn and get immediate feedback. • Source code for all example programs in the book. • Answers to quick check exercises. • Glossary of key terms. • Recent News links relevant to computer science. • AdditionalTopics such as more on swing and an introduction to data structures. Acknowledgments First, I would like to thank the following reviewers for their comments, suggestions, and encouragement. Wu Focus Group—Jackson Hole, WY Elizabeth Adams, James Madison University GianMario Besana, Depaul University Michael Buckley, State University of New York, Buffalo James Cross, Auburn University Priscilla Dodds, Georgia Perimeter College Christopher Eliot, University of Massachusetts-Amherst Joanne Houlahan, John Hopkins University Len Myers, California Polytechnic State University, San Luis Obispo Hal Perkins, University of Washington William Shea, Kansas State University Marge Skubic, University of Missouri, Columbia Bill Sverdlik, Eastern Michigan University Suzanne Westbrook, University of Arizona wu23399_fm.qxd 1/10/07 11:55 Page xxiii
- 28. xxiv Preface Reviewers Ajith, Abraham, Oklahoma State University Elizabeth Adams, James Madison University David L. Atkins, University of Oregon GianMario Besana, DePaul University Robert P. Burton, Brigham Young University Michael Buckley, State University of New York, Buffalo Rama Chakrapani, Tennessee Technological University Teresa Cole, Boise State University James Cross, Auburn University Priscilla Dodds, Georgia Perimeter College Kossi Delali Edoh, Montclair State University Christopher Eliot, University of Massachusetts-Amherst Michael Floeser, Rochester Institute of Technology Joanne Houlahan, John Hopkins University Michael N. Huhns, University of South Carolina Eliot Jacobson, University of California, Santa Barbara Martin Kendall, Montgomery Community College Mike Litman, Western Illinois University Len Myers, California Polytechnic State University, San Luis Obispo Jun Ni, University of Iowa Robert Noonan, College of William and Mary Jason S. O’Neal, Mississippi College Hal Perkins, University of Washington Gerald Ross, Lane Community College William Shea, Kansas State University Jason John Schwarz, North Carolina State University Marge Skubic, University of Missouri, Columbia Bill Sverdlik, Eastern Michigan University Peter Stanchev, Kettering University Krishnaprasad Thirunarayan, Wright State University David Vineyard, Kettering University Suzanne Westbrook, University of Arizona Melissa Wiggins, Mississippi College Zhiguang Xu, Valdosta State University. The following reviewers have provided feedback on the chapters new to this comprehensive edition: Eric Matson, Wright State University Tim Margush, University of Akron Roxanne Canosa, Rochester Institute of Technology Ivan Bajic, San Diego State University Carolyn Miller, North Carolina State Sunil Prabhakar, Purdue University Weining Zhang, University of Texas, San Antonio wu23399_fm.qxd 1/10/07 11:56 Page xxiv
- 29. Preface xxv Personal Story In September, 2001, I changed my name for personal reasons. Prof C. Thomas Wu is now Prof Thomas W. Otani. To maintain continuity and not to confuse peo- ple, we continue to publish the book under my former name. For those who care to find out a little about my personal history can do so by visiting my web- site (www.drcaffeine.com). wu23399_fm.qxd 1/10/07 11:56 Page xxv
- 30. wu23399_fm.qxd 1/10/07 11:56 Page xxvi
- 31. O b j e c t i v e s After you have read and studied this chapter,you should be able to 1 0 • State briefly a history of computers. • Name and describe five major components of the computer. • Convert binary numbers to decimal numbers and vice versa. • State the difference between the low-level and high-level programming languages. Introduction to Computers and Programming Languages wu23392_ch00.qxd 12/12/06 17:23 Page 1
- 32. 2 Chapter 0 Introduction to Computers and Programming Languages efore we embark on our study of computer programming, we will present some background information on computers and programming languages in this optional chapter. We provide a brief history of computers from the early days to present and describe the components found in today’s computers. We also present a brief history of programming languages from low-level machine languages to today’s object- oriented languages. 0.1 A History of Computers Humans have evolved from a primitive to a highly advanced society by continually inventing tools. Stone tools, gunpowder, wheels, and other inventions have changed the lives of humans dramatically. In recent history, the computer is arguably the most important invention. In today’s highly advanced society, computers affect our lives 24 hours a day: class schedules are formulated by computers, student records are maintained by computers, exams are graded by computers, dorm security sys- tems are monitored by computers, and numerous other functions that affect us are controlled by computers. Although the first true computer was invented in the 1940s, the concept of a computer is actually more than 160 years old. Charles Babbage is credited with inventing a precursor to the modern computer. In 1823 he received a grant from the British government to build a mechanical device he called the Difference Engine, intended for computing and printing mathematical tables. The device was based on rotating wheels and was operated by a single crank. Unfortunately, the technology of the time was not advanced enough to build the device. He ran into difficulties and eventually abandoned the project. But an even more grandiose scheme was already with him. In fact, one of the reasons he gave up on the Difference Engine may have been to work on his new con- cept for a better machine. He called his new device the Analytical Engine. This device, too, was never built. His second device also was ahead of its time; the tech- nology did not yet exist to make the device a reality. Although never built, the Ana- lytical Engine was a remarkable achievement because its design was essentially based on the same fundamental principles of the modern computer. One principle that stands out was its programmability. With the Difference Engine, Babbage would have been able to compute only mathematical tables, but with the Analytical Engine he would have been able to compute any calculation by inputting instructions on punch cards. The method of inputting programs to computers on punch cards was actually adopted for real machines and was still in wide use as late as the 1970s. The Analytical Engine was never built, but a demonstration program was written by Ada Lovelace, a daughter of the poet Lord Byron. The programming lan- guage Ada was named in honor of Lady Lovelace, the first computer programmer. In the late 1930s John Atanasoff of Iowa State University, with his graduate student Clifford Berry, built the prototype of the first automatic electronic calculator. I n t r o d u c t i o n B Charles Babbage Difference Engine Analytical Engine Ada Lovelace wu23392_ch00.qxd 12/12/06 17:23 Page 2
- 33. 0.1 A History of Computers 3 One innovation of their machine was the use of binary numbers. (We discuss binary numbers in Sec. 0.2.)At around the same time, HowardAiken of Harvard University was working on the Automatic Sequence-Controlled Calculator, known more com- monly as MARK I, with support from IBM and the U.S. Navy. MARK I was very similar to the Analytical Engine in design and was described as “Babbage’s dream come true.” MARK I was an electromechanical computer based on relays. Mechanical relays were not fast enough, and MARK I was quickly replaced by machines based on electronic vacuum tubes. The first completely electronic computer, ENIAC I (Electronic Numerical Integrator And Calculator), was built at the University of Pennsylvania under the supervision of John W. Mauchly and J. Presper Eckert. Their work was influenced by the work of John Atanasoff. ENIAC I was programmed laboriously by plugging wires into a control panel that resembled an old telephone switchboard. Programming took an enor- mous amount of the engineers’ time, and even making a simple change to a pro- gram was a time-consuming effort. While programming activities were going on, the expensive computer sat idle. To improve its productivity, John von Neumann of Princeton University proposed storing programs in the computer’s memory. This stored program scheme not only improved computation speed but also al- lowed far more flexible ways of writing programs. For example, because a pro- gram is stored in the memory, the computer can change the program instructions to alter the sequence of the execution, thereby making it possible to get different results from a single program. We characterized these early computers with vacuum tubes as first-generation computers. Second-generation computers, with transistors replacing the vacuum tubes, started appearing in the late 1950s. Improvements in memory devices also increased processing speed further. In the early 1960s, transistors were replaced by integrated circuits, and third-generation computers emerged. A single integrated circuit of this period incorporated hundreds of transistors and made the construction of minicomputers possible. Minicomputers are small enough to be placed on desk- tops in individual offices and labs. The early computers, on the other hand, were so huge that they easily occupied the whole basement of a large building. Advancement of integrated circuits was phenomenal. Large-scale integrated circuits, commonly known as computer chips or silicon chips, packed the power equivalent to thousands of transistors and made the notion of a “computer on a sin- gle chip” a reality. With large-scale integrated circuits, microcomputers emerged in the mid-1970s. The machines we call personal computers today are descendants of the microcomputers of the 1970s. The computer chips used in today’s personal computers pack the power equivalent to several millions of transistors. Personal computers are fourth-generation computers. Early microcomputers were isolated, stand-alone machines. The word per- sonal describes a machine as a personal device intended to be used by an individual. However, it did not take long to realize there was a need to share computer resources. For example, early microcomputers required a dedicated printer. Wouldn’t it make more sense to have many computers share a single printer? Wouldn’t it also make sense to share data among computers, instead of duplicating the same data on MARK I ENIAC I stored program generations of computers wu23392_ch00.qxd 12/12/06 17:23 Page 3
- 34. individual machines? Wouldn’t it be nice to send electronic messages between the computers? The notion of networked computers arose to meet these needs. Computers of all kinds are connected into a network. A network that connects computers in a single building or in several nearby buildings is called a local-area network or LAN. A network that connects geographically dispersed computers is called a wide-area network or WAN. These individual networks can be connected further to form interconnected networks called internets. The most famous internet is simply called the Internet. The Internet makes the sharing of worldwide informa- tion possible and easy. The hottest tool for viewing information on the Internet is a Web browser. A Web browser allows you to experience multimedia information consisting of text, audio, video, and other types of information. We will describe how Java is related to the Internet and Web browsers in Section 0.4. 4 Chapter 0 Introduction to Computers and Programming Languages network LAN WAN internet 1. Who was the first computer programmer? 2. Who designed the Difference Engine and Analytical Engine? 3. How many generations of computers are there? 0.2 Computer Architecture A typical computer today has five basic components: RAM, CPU, storage devices, I/O (input/output) devices, and communication devices. Figure 0.1 illustrates these five components. Before we describe the components of a computer, we will explain the binary numbering system used in a computer. Binary Numbers To understand the binary number system, let’s first review the decimal number sys- tem in which we use 10 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. To represent a number in the decimal system, we use a sequence of one or more of these digits. The value that each digit in the sequence represents depends on its position. For example, consider the numbers 234 and 324. The digit 2 in the first number represents 200, whereas the digit 2 in the second number represents 20. A position in a sequence has a value that is an integral power of 10. The following diagram illustrates how the If you want to learn more about the history of computing,there is a wealth of information available on the Web.You can start your exploration from www.yahoo.com/Computers_and_Internet/History For more information on the pioneers of computers,visit en.wikipedia.org/wiki/category:Computer_pioneers wu23392_ch00.qxd 12/12/06 17:23 Page 4
- 35. 0.2 Computer Architecture 5 values of positions are determined: The value of a decimal number (represented as a sequence of digits) is the sum of the digits, multiplied by their position values, as illustrated: 2 102 4 101 8 100 7 101 2 100 4 10 8 1 7 110 200 40 8 710 248.7 2 102 4 101 8 100 • 7 101 104 103 102 101 100 Decimal Point Position Values 101 102 • • • • • • 103 • Figure 0.1 A simplified view of an architecture for a typical computer. Output Devices Communication Devices Input Devices RAM CPU Storage Devices Printer (output device) Monitor (output device) Main Unit (housing CPU, RAM, storage devices, and communication devices) Mouse (input device) Keyboard (input device) wu23392_ch00.qxd 12/12/06 17:23 Page 5
- 36. In the decimal number system, we have 10 symbols, and the position values are integral powers of 10. We say that 10 is the base or radix of the decimal number system. The binary number system works the same as the decimal number system but uses 2 as its base. The binary number system has two digits (0 and 1) called bits, and position values are integral powers of 2. The following diagram illustrates how the values of positions are determined in the binary system: The value of a binary number (represented as a sequence of bits) is the sum of the bits, multiplied by their position values, as illustrated: 1 22 0 21 1 20 1 21 1 4 0 2 1 1 1 12 4 0 1 12 5.5 So the binary number 101.1 is numerically equivalent to the decimal num- ber 5.5. This illustration shows how to convert a given binary number to the decimal equivalent. How about converting a given decimal number to its binary equivalent? The following steps show how to convert a decimal number (only the whole numbers) to the equivalent binary number. The basic idea goes something like this: 1. Divide the number by 2. 2. The remainder is the bit value of the 20 position. 3. Divide the quotient by 2. 4. The remainder is the bit value of the 21 position. 5. Divide the quotient by 2. 6. The remainder is the bit value of the 22 position. 7. Repeat the procedure until you cannot divide any further, that is, until the quotient becomes 0. 1 22 0 21 1 20 • 1 21 24 23 • • • • • • 22 21 20 Binary Point Position Values • 21 22 23 6 Chapter 0 Introduction to Computers and Programming Languages base-2 numbers binary number bits binary-to- decimal conversion decimal-to- binary conversion wu23392_ch00.qxd 12/12/06 17:23 Page 6
- 37. 0.2 Computer Architecture 7 When you pay closer attention to the on/off switch on computers and other electronic devices,you should notice an icon like this This is a stylized representation of binary digits 0 and 1. RAM Random access memory or RAM is a repository for both program instructions and data manipulated by the program during execution. RAM is divided into cells, with each cell having a unique address. Typically, each cell consists of 4 bytes (B), and a single byte (1 B) in turn consists of 8 bits. Each bit, which can be either on or off, represents a single binary digit. RAM is measured by the number of bytes it contains. For example, 128 kilobytes (KB) of RAM contains 128 1024 131,072 B because 1 KB is equal to 210 1024 B. Notice that 1 K is not equal to 103 , although 103 1000 is a close approximation to 210 1024. The first IBM PC introduced in 1981 came with 16 KB of RAM, and the first Macintosh com- puter introduced in 1984 came with 128 KB of RAM. In contrast, a typical PC today has anywhere from 128 MB to 512 MB of RAM. Given that 1 MB is equal to 1024 KB, we know that 256 MB means 256 1024 KB 262,144 KB 262,144 1024 B 268,435,456 B. RAM byte The following diagram illustrates the conversion of decimal number 25. Division Division Division Division Division #5 #4 #3 #2 #1 24 23 22 21 20 16 8 0 0 1 25 The binary system is more suitable for computers than the decimal system be- cause it is far easier to design an electrical device that can distinguish two states (bits 0 and 1) than 10 states (digits 0 through 9). For example, we can represent 1 by turning the switch on and 0 by turning the switch off. In a real computer, 0 is repre- sented by electrical voltage below a certain level and 1 by electrical voltage at or above this level. 12 21 2 5 1 24 1 6 21 1 2 1 12 0 3 21 6 1 6 0 1 21 3 1 2 1 0 21 1 1 0 1 wu23392_ch00.qxd 12/12/06 17:23 Page 7
- 38. CPU The central processing unit or CPU is the brain of a computer. The CPU is the com- ponent that executes program instructions by fetching an instruction (stored in RAM), executing it, fetching the next instruction, executing it, and so on until it en- counters an instruction to stop. The CPU contains a small number of registers, which are high-speed devices for storing data or instructions temporarily. The CPU also contains the arithmetic-logic unit (ALU), which performs arithmetic operations such as addition and subtraction and logical operations such as comparing two numbers. CPUs are characterized by their clock speeds. For example, in the Intel Pentium 200, the CPU has a clock speed of 200 megahertz (MHz). The hertz is a unit of frequency equal to 1 cycle per second. A cycle is a period of time between two on states or off states. So 200 MHz equals 200,000,000 cycles per second. The fastest CPU for commercially available personal computers was around 200 MHz in 1997 when the first edition of this textbook was published. But by the beginning of 1998, many vendors started selling 300-MHz machines. And in a mere 6 months, by the middle of 1998, the top-of-the-line personal computers were 400-MHz ma- chines. As of this writing in late 2002, we see computers with 2.0-GHz (2000-MHz) CPU being advertised and sold. The increase of the CPU speed in the last two decades is truly astonishing. The clock speed of the Intel 8080, the CPU introduced in 1974 that started the PC revolution, was a mere 2 MHz. In contrast, the clock speed of the Intel Pentium 4 introduced in 2001 was 2 GHz (2000 MHz). Table 0.1 lists some of the Intel processors. I/O Devices Input/output or I/O devices allow communication between the user and the CPU. Input devices such as keyboards and mice are used to enter data, programs, and commands in the CPU. Output devices such as monitors and printers are used to display or print information. Other I/O devices include scanners, bar code readers, magnetic strip readers, digital video cameras, and musical instrument digital inter- face (MIDI) devices. Storage Devices Storage devices such as disk and tape drives are used to store data and programs. Sec- ondary storage devices are called nonvolatile memory, while RAM is called volatile memory. Volatile means the data stored in a device will be lost when the power to the device is turned off. Being nonvolatile and much cheaper than RAM, secondary stor- age is an ideal medium for permanent storage of large volumes of data. A secondary storage device cannot replace RAM, though, because secondary storage is far slower in data access (getting data out and writing data in) compared to RAM. The most common storage device today for personal computers is a disk drive. There are two kinds of disks: hard and floppy (also known as diskettes). Hard disks provide much faster performance and larger capacity, but are normally not re- movable; that is, a single hard disk is permanently attached to a disk drive. Floppy disks, on the other hand, are removable, but their performance is far slower and their capacity far smaller than those of hard disks. As the standard floppy disks can 8 Chapter 0 Introduction to Computers and Programming Languages CPU register clock speed I/O devices nonvolatile and volatile memory wu23392_ch00.qxd 12/12/06 17:23 Page 8
- 39. store only up to approximately 1.44 MB, they are becoming less useful in today’s world of multimegabyte image and sound files. They are fast becoming obsolete, and hardly anybody uses them anymore. Removable storage media with much higher capacity such as zip disks (capable of holding 100 to 250 MB of data) re- placed floppy disks in late 1990s. Computer technology moves so quickly that zip disks themselves are already becoming obsolete. The most common form of portable storage medium today (2006) is a compact USB flash drive, whose capac- ity ranges from 125 MB to 16 GB. Hard disks can store a huge amount of data, typically ranging from 20 GB (gigabyte; 1 GB 1024 MB) to 80 GB for a standard desktop PC in 2002. Portable and removable hard disk drives, with performance and capacity that rival those of nonremovable hard disks, are also available, but their use is not widespread. Compact disks (CDs) are very popular today for storing massive amounts of data, approximately 700 MB. Many software packages we buy today—computer 0.2 Computer Architecture 9 Table Table 0.1 A table of Intel processors.For some CPUs,several types with different clock speeds are possible.In such case,only the fastest clock speed is shown.For more information on Intel CPUs,visit http://www.intel.com. Date Clock Speed CPU Introduced (MHz) 4004 11/15/71 0.108 8008 4/1/72 0.200 1970s 8080 4/1/74 2 8088 6/1/79 8 80286 2/1/82 12 1980s 80386SX 6/16/88 16 80486DX 4/10/89 25 Pentium 3/22/93 66 Pentium Pro 11/1/95 200 1990s Pentium II 5/7/97 300 Pentium II Xeon 6/29/98 400 Pentium III 10/25/99 733 Xeon 9/25/01 2000 2000s Pentium 4 4/27/01 2000 Itanium 2 7/8/02 1000 Pentium 4 Extreme 2/2/04 3400 Edition Core 2 Extreme 7/27/06 3200 wu23392_ch00.qxd 12/12/06 17:23 Page 9
- 40. games, word processors, and others—come with a single CD. Before the CD became apopularstoragedeviceforcomputers,somesoftwarecamewithmorethan20floppy diskettes. Because of the massive storage capacity of the CD, most computer vendors eliminated printed manuals altogether by putting the manuals on the CD. 10 Chapter 0 Introduction to Computers and Programming Languages Communication Devices A communication device connects the personal computer to an internet. The most common communication device for computers at home and in small offices is the modem. A modem, which stands for modulator-demodulator, is a device that con- verts analog signals to digital and digital signals to analog. By using a modem, a computer can send to and receive data from another computer over the phone line. The most critical characteristic of a modem is its transmission speed, which is mea- sured in bits per second (bps). A typical speed for a modem is 56,000 bps, com- monly called a 56K modem. Under an ideal condition (no line noise or congestion), a 56K modem can transfer a 1 MB file in about 21 ⁄2 minutes. Frequently, though, the actual transfer rate is much lower than the possible maximum. So-called DSL and cable modems are not truly modems because they transfer data strictly in digital mode, which allows for much faster connection speeds of 144K or above. High- speed satellite connection to the Internet is also available today. A communication device for connecting a computer to a LAN is a network interface card (NIC). A NIC can transfer data at a much faster rate than the fastest modem. For instance, a type of NIC called 10BaseT can transfer data at the rate of 10 Mbps over the network. Traditional networks are connected, or wired, by the cables. Increasingly, networks are connected wirelessly, where data are carried over radio waves. Wireless networking is called WiFi or 802.11 networking. Today you will find wireless networking almost universally available at airports and hotels. communication device 1. Name five major components of a computer. 2. What is the difference between volatile and nonvolatile memory? 3. What does the acronym CPU stand for? 4. How many bytes does the 64 KB RAM have? 5. Which device connects a computer to the Internet using a phone line? Today we see more and more companies are even eliminating CDs and promoting “boxless”online distribution of software.With this scheme,we go to their websites and download the software,after paying for it with our credit card.Maybe someday we may be able to buy textbooks in the same manner and stop carrying 20 lb of dead trees in our backpacks. wu23392_ch00.qxd 12/12/06 17:23 Page 10
- 41. 0.3 Programming Languages Programming languages are broadly classified into three levels: machine languages, assembly languages, and high-level languages. Machine language is the only pro- gramming language the CPU understands. Each type of CPU has its own machine language. For example, the Intel Pentium and Motorola PowerPC understand differ- ent machine languages. Machine-language instructions are binary-coded and very low level—one machine instruction may transfer the contents of one memory loca- tion into a CPU register or add numbers in two registers. Thus we must provide many machine-language instructions to accomplish a simple task such as finding the aver- age of 20 numbers.Aprogram written in machine language might look like this: 10110011 00011001 01111010 11010001 10010100 10011111 00011001 01011100 11010001 10010000 10111011 11010001 10010110 One level above machine language is assembly language, which allows “higher-level” symbolic programming. Instead of writing programs as a sequence of bits, assembly language allows programmers to write programs by using sym- bolic operation codes. For example, instead of 10110011, we use MV to move the contents of a memory cell into a register. We also can use symbolic, or mnemonic, names for registers and memory cells. A program written in assembly language might look like this: MV 0, SUM MV NUM, AC ADD SUM, AC STO SUM, TOT Since programs written in assembly language are not recognized by the CPU, we use an assembler to translate programs written in assembly language into machine-language equivalents. Compared to writing programs in machine lan- guage, writing programs in assembly language is much faster, but not fast enough for writing complex programs. High-level languages were developed to enable programmers to write pro- grams faster than when using assembly languages. For example, FORTRAN (FORmula TRANslator), a programming language intended for mathematical com- putation, allows programmers to express numerical equations directly as X = (Y + Z) / 2 COBOL (COmmon Business-Oriented Language) is a programming language in- tended for business data processing applications. FORTRAN and COBOL were de- veloped in the late 1950s and early 1960s and are still in use. BASIC (Beginners All-purpose Symbolic Instructional Code) was developed specifically as an easy language for students to learn and use. BASIC was the first high-level language 0.3 Programming Languages 11 machine language machine code assembly code assembler high-level code high-level languages assembly language wu23392_ch00.qxd 12/12/06 17:23 Page 11
- 42. available for microcomputers. Another famous high-level language is Pascal, which was designed as an academic language. Since programs written in a high-level lan- guage are not recognized by the CPU, we must use a compiler to translate them to assembly language equivalents. The programming language C was developed in the early 1970s at ATT Bell Labs. The C++ programming language was developed as a successor of C in the early 1980s to add support for object-oriented programming. Object-oriented pro- gramming is a style of programming gaining wider acceptance today. Although the concept of object-oriented programming is old (the first object-oriented program- ming language, Simula, was developed in the late 1960s), its significance wasn’t realized until the early 1980s. Smalltalk, developed at Xerox PARC, is another well-known object-oriented programming language. The programming language we use in this book is Java, the newest object-oriented programming language, developed at Sun Microsystems. 0.4 Java Java isanewobject-orientedlanguagethatisreceivingwideattentionfrombothindus- try and academia. Java was developed by James Gosling and his team at Sun Microsys- tems in California. The language was based on C and C++ and was originally intended for writing programs that control consumer appliances such as toasters, microwave ovens,andothers.ThelanguagewasfirstcalledOak,namedaftertheoaktreeoutsideof Gosling’s office, but the name was already taken, so the team renamed it Java. Java is often described as a Web programming language because of its use in writing programs called applets that run within a Web browser. That is, you need a Web browser to execute Java applets. Applets allow more dynamic and flexible dis- semination of information on the Internet, and this feature alone makes Java an at- tractive language to learn. However, we are not limited to writing applets in Java. We can write Java applications also. A Java application is a complete stand-alone program that does not require a Web browser. A Java application is analogous to a program we write in other programming languages. In this book, we focus on Java applications because our objective is to teach the fundamentals of object-oriented programming that are applicable to all object-oriented programming languages. We chose Java for this textbook mainly for its clean design. The language de- signers of Java took a minimalist approach; they included only features that are in- dispensable and eliminated features that they considered excessive or redundant. This minimalist approach makes Java a much easier language to learn than other object-oriented programming languages. Java is an ideal vehicle for teaching the fundamentals of object-oriented programming. 12 Chapter 0 Introduction to Computers and Programming Languages compiler Java applet application • Charles Babbage invented the Difference Engine and Analytical Engine, precursors to the modern computer. • Ada Lovelace is considered the first computer programmer. • The first two modern computers were MARK I and ENIAC I. S u m m a r y wu23392_ch00.qxd 12/12/06 17:23 Page 12
- 43. • John von Neumann invented the stored-program approach of executing programs. • Computers are connected into a network. Interconnected networks are called internets. • Binary numbers are used in computers. • A typical computer consists of five components: RAM, CPU, storage devices, I/O devices, and communication devices. • There are three levels of programming languages: machine, assembly, and high-level. • Java is one of the newest high-level programming languages in use today. This textbook teaches how to program using Java. Exercises 13 K e y C o n c e p t s network LAN WAN internets and Internet CPU RAM I/O devices communication devices binary numbers binary-to-decimal conversion machine language assembly language assembler high-level language compiler Java E x e r c i s e s 1. Visit your school’s computer lab or a computer store, and identify the different components of the computers you see. Do you notice any unique input or output devices? 2. Visit your school’s computer lab and find out the CPU speed, RAM size, and hard disk capacity of its computers. 3. Convert these binary numbers to decimal numbers. a. 1010 b. 110011 c. 110.01 d. 111111 4. Convert these decimal numbers to binary numbers. a. 35 b. 125 c. 567 d. 98 wu23392_ch00.qxd 12/12/06 17:23 Page 13
- 44. 5. What is the maximum decimal number you can represent in 4 bits? 16 bits? N bits? 6. If a computer has 128 MB of RAM, how many bytes are there? 7. How do high-level programming languages differ from low-level programming languages? 8. Consider a hypothetical programming language called Kona. Using Kona, you can write a program to compute and print out the sum of 20 integers entered by the user: let sum = 0; repeat 20 times [ let X = next input; add X to sum; ] printout sum; Is Kona a high-level language? Why or why not? 14 Chapter 0 Introduction to Computers and Programming Languages wu23392_ch00.qxd 12/12/06 17:23 Page 14
- 45. Introduction to Object-Oriented Programming and Software Development O b j e c t i v e s After you have read and studied this chapter,you should be able to • Name the basic components of object- oriented programming. • Differentiate classes and objects. • Differentiate class and instance methods. • Differentiate class and instance data values. • Draw program diagrams using icons for classes,objects,and other components of object-oriented programming. • Describe the significance of inheritance in object-oriented programs. • Name and explain the stages of the software life cycle. 15 1 wu23399_ch01.qxd 12/12/06 17:24 Page 15
- 46. efore we begin to write actual programs, we need to introduce a few basic concepts of object-oriented programming (OOP), the style of programming we teach in this book. The purpose of this chapter is to give you a feel for object-oriented program- ming and to introduce a conceptual foundation of object-oriented programming.You may want to refer to this chapter as you progress through the book. What we discuss in the next four sections is independent of any particular programming language. 16 Chapter 1 Introduction to Object-Oriented Programming and Software Development I n t r o d u c t i o n B object- oriented programming object Those of you who have some experience in programming, whether object- oriented or non-object-oriented,will probably find many similarities between Java and the programming languages you already know.This similarity may accelerate your learning process, but in many cases what seems to be similar at first may turn out to be quite different. So please do not jump to any conclusions about similarity prematurely. Another purpose of this chapter is to introduce the software development process. To be able to write programs, knowledge of the components of object- oriented programs is not enough. We must learn the process of developing pro- grams. We will present a brief introduction to the software development process in this chapter. 1.1 Classes and Objects The two most important concepts in object-oriented programming are the class and the object. In the broadest term, an object is a thing, both tangible and intangi- ble, that we can imagine. A program written in object-oriented style will consist of interacting objects. For a program to keep track of student residents of a college dormitory, we may have many Student, Room, and Floor objects. For another pro- gram to keep track of customers and inventory for a bicycle shop, we may have Customer, Bicycle, and many other types of objects. An object is comprised of data and operations that manipulate these data. For example, a Student object may con- sist of data such as name, gender, birth date, home address, phone number, and age and operations for assigning and changing these data values. We will use the nota- tion shown in Figure 1.1 throughout the book to represent an object. The notation we used in the book is based on the industry standard notation called UML, which stands for Unified Modeling Language. In some of the illustrations, we relax the rules of UML slightly for pedagogy. Almost all nontrivial programs will have many objects of the same type. For example, in the bicycle shop program we expect to see many Bicycle and other objects. Figure 1.2 shows two Bicycle objects with the names Moto-1 and Moto-2 and one Customer object with the name Jon Java. wu23399_ch01.qxd 12/12/06 17:24 Page 16
- 47. Inside a program we write instructions to create objects. For the computer to be able to create an object, we must provide a definition, called a class. A class is a kind of mold or template that dictates what objects can and cannot do. An object is called an instance of a class. An object is an instance of exactly one class. An instance of a class belongs to the class. The two Bicycle objects Moto-1 and Moto-2 are instances of the Bicycle class. Once a class is defined, we can create as many instances of the class as a program requires. 1.1 Classes and Objects 17 class instance Object name We use a rectangle to represent an object and place the underlined name of the object inside the rectangle. Example: account1 This is an object named account1. Figure 1.1 A graphical representation of an object. Jon Java : Customer Moto-2 : Bicycle Moto-1 : Bicycle An object name is followed by the class name. Figure 1.2 Two Bicycle objects with the names Moto-1 and Moto-2 and one Customer object with the name Jon Java. A class must be defined before you can create an instance (object) of the class. Figure 1.3 shows a diagram that we will use throughout the book to represent a class. 1. Draw an object diagram for a Person class and two Person objects, Ms. Latte and Mr. Espresso. 2. What must be defined before you can create an object? wu23399_ch01.qxd 12/12/06 17:24 Page 17
- 48. 1.2 Messages and Methods In writing object-oriented programs we must first define classes, and while the pro- gram is running, we use the classes and objects from these classes to accomplish tasks. A task can range from adding two numbers, to computing an interest payment for a college loan, to calculating the reentry angle of a space shuttle. To instruct a class or an object to perform a task, we send a message to it. For example, we send a message deposit to an Account object to deposit $100. For a class or an object to process the message, it must be programmed ac- cordingly. You cannot just send a message to any class or object. You can send a message only to the classes and objects that understand the message you send. For a class or an object to process the message it receives, it must possess a matching method, which is a sequence of instructions that a class or an object follows to perform a task. A method defined for a class is called a class method, and a method defined for an object is an instance method. 18 Chapter 1 Introduction to Object-Oriented Programming and Software Development Example: We use a rectangle to represent a class with its name appearing inside the rectangle. Class Name Notice the name of a class is not underlined while the name of an object is. Account Figure 1.3 A graphical representation of a class. Many beginning programmers may not see the distinction between the class and object as clearly as the more experienced programmers do.It may be helpful to compare the class and object to a woodcut and the prints produced from the woodcut.A woodcut is a block of wood engraved with a design for printing.Once you have a woodcut,you can make as many prints as you wish.Similarly,once you have a class,you can make as many objects from the class.Also,just as you cannot make prints without having a woodcut,you cannot create an object without first defining a class.For sample prints by the 19th-century Japanese artist Hiroshige,visit http://www.ibiblio.org/wm/paint/auth/hiroshige/ Another helpful analogy is a robot factory.A factory is a class,and the robots produced from the factory are the objects of the class.To create robots (instance),we need the factory (class) first.Those interested in mobile robots can visit http://www.ai.mit.edu/projects/mobile-robots/robots.html message method class and instance methods wu23399_ch01.qxd 12/12/06 17:24 Page 18
- 49. Let’s look at an example of an instance method first. Suppose a method called walk is defined for a Robot object and instructs the robot to walk a designated dis- tance. With this method defined, we can send the message walk to a Robot object, along with the distance to be walked. A value we pass to an object is called an argument of a message. Notice that the name of the message we send to an object or a class must be the same as the method’s name. In Figure 1.4 we represent the send- ing of a message. The diagram in Figure 1.4 illustrates one-way communication; that is, an object carries out the requested operation (it walks the designated distance) but does not respond to the message sender. In many situations we need a reply in which an object responds by returning a value to the message sender. For exam- ple, suppose we want to know the distance from a robot to its nearest obstacle. The designer of a robot may include a method getObstacleDistance that returns the desired value. The diagram in Figure 1.5 shows a method that returns a value to the message sender. Instead of returning a numerical value, a method can re- port back the status of the requested operation. For example, a method walk can be defined to return the status success/fail to indicate whether the specified distance was covered successfully or not (e.g., it fails when the robot bumps into an obstacle). Now let’s look at an example of class methods. The class method getMaxi- mumSpeed shown in Figure 1.6 returns the maximum possible speed of all Robot objects. A method such as getMaximumSpeed that deals with collective information about the instances of a class is usually defined as a class method. So we define an instance method for a task that pertains to an individual instance and a class method for a task that pertains to all instances. 1.2 Messages and Methods 19 argument walk(25) fido : Robot Message walk with the argument 25. Figure 1.4 Sending the message walk to a Robot object. getObstacleDistance( ) distance fido : Robot This shows that we are not sending any argument. This shows the value distance is returned as a response to the message. Figure 1.5 The result distance is returned to the sender of the message. wu23399_ch01.qxd 12/12/06 17:24 Page 19
- 50. 20 Chapter 1 Introduction to Object-Oriented Programming and Software Development getMaximumSpeed( ) maximum speed Robot Figure 1.6 The maximum possible speed of all Robot objects is returned by the class method getMaximumSpeed. 1. Draw an object diagram of an Account object with instance methods deposit and withdraw. 2. Is the getObstacleDistance method an instance or a class method? 1.3 Class and Instance Data Values Suppose the method deposit of an Account object instructs the object to add a given amount to the current balance. Where does the object keep the current balance? Remember that an object is comprised of data values and methods. Analogous to defining class and instance methods, we can define class and instance data values. For example, we define an instance data value current balance for Account objects to record the current balance. Figure 1.7 shows three Account objects with their data values current balance. Notice that they all have the same data value current balance.All instances of the same class will possess the same set of data values. The actual dollar amounts for current balance, as the diagram illustrates, differ from one instance to another. Items such as opening balance and account number are other possible instance data values for Account objects. A class data value is used to represent information shared by all instances or to represent collective information about the instances. For example, if every account must maintain a minimum balance of, say, $100, we can define a class data value minimum balance. An instance can access the class data values of the class to which it belongs, so every Account object can access the class data value minimum balance. Jill’s : Account 1304.98 current balance Jack’s : Account 354.00 current balance John’s : Account 908.55 current balance Figure 1.7 Three Account objects possess the same data value current balance, but the actual dollar amounts differ. instance data value class data value wu23399_ch01.qxd 12/12/06 17:24 Page 20
- 51. Figure 1.8 shows how we represent a class data value. Notice that we underline the class data value. Because the objects of a class are underlined, and the class data val- ues are accessible to all objects of the class, we likewise underline the class data value to show this relationship. Data values are also called data members because they belong to a class or instance of the class. To appreciate the significance of a class data value, let’s see what happens if we represent minimum balance as an instance data value. Figure 1.9 shows three Account objects having different dollar amounts for the current balance but the same dollar amount for the minimum balance. Obviously, this duplication of mini- mum balance is redundant and wastes space. Consider, for example, what happens if the bank raises the minimum balance to $200. If there are 100 Account objects, then all 100 copies of minimum balance must be updated. We can avoid this by defining minimum balance as a class data value. Figure 1.10 shows another exam- ple where the opening and closing times are shared by all cafeterias on campus. There are two types of data values: those that can change over time and those that cannot. A data value that can change is called a variable, and one that cannot 1.3 Class and Instance Data Values 21 John’s : Account 908.55 current balance Jill’s : Account 1304.98 current balance Account minimum balance 100.00 Jack’s : Account 354.00 current balance Notice the class data value is underlined to show the fact that this value is accessible to individual objects, which are underlined. Figure1.8 Three Account objects sharing information (minimumbalance $100) stored as a class data value. data member variable John’s : Account 908.55 current balance minimum balance 100.00 Jill’s : Account 1304.98 current balance minimum balance 100.00 Jack’s : Account 354.00 current balance minimum balance 100.00 Figure1.9 ThreeAccountobjectsduplicatinginformation(minimumbalance $100)ininstancedatavalues. wu23399_ch01.qxd 12/12/06 17:24 Page 21
- 52. change is a constant. Figure 1.11 illustrates how we represent and distinguish be- tween variables and constants. We use the keyword frozen for constants to indicate that they cannot change. Notice that we now have four kinds of data values: class variables, class constants, instance variables, and instance constants. 22 Chapter 1 Introduction to Object-Oriented Programming and Software Development Union : Cafeteria 1917.34 revenue West : Cafeteria 2306.99 revenue QuikBite : Cafeteria 430.75 revenue Cafeteria opens 0600 closes 2100 Figure 1.10 Three Cafeteria objects sharing the same opening and closing times,stored as class data values. John’s : Account 908.55 current balance opening balance {frozen} 246.00 Jill’s : Account 1304.98 current balance opening balance {frozen} 50.00 Account 100.00 minimum balance account prefix {frozen} 6427 Jack’s : Account 354.00 current balance opening balance {frozen} 100.00 We assume this number is a prefix to the account number of all accounts, and the prefix never changes. This keyword indicates the value is locked and cannot be changed. Figure 1.11 Graphical representations for four types of data values:class variable,class constant,instance variable,and instance constant. constant wu23399_ch01.qxd 12/12/06 17:24 Page 22
- 53. 1.4 Inheritance When we used the Account class and its instances to illustrate object-oriented con- cepts, some of you were probably thinking about checking accounts, while others may have been thinking about savings accounts. We did not distinguish between the two in the examples. But when we look at the problem a little more carefully, we will realize that in fact these two types of accounts are different, even though they share many features. In general, using only a single class to model two or more entities that are similar but different is not good design. In object-oriented programming, we use a mechanism called inheritance to design two or more entities that are different but share many common features. First we define a class that contains the common fea- tures of the entities. Then we define classes as an extension of the common class inheriting everything from the common class. We call the common class the superclass and all classes that inherit from it subclasses. We also call the superclass an ancestor and the subclass a descendant. Other names for superclass and subclass are base class and derived class, respectively. For the bank example, we can define a superclass Account and then define Savings and Checking as subclasses of Account. We represent the superclass and its subclasses as shown in Figure 1.12. Notice that we draw arrows from each subclass to its superclass because a subclass can refer to items defined in its superclass, but not vice versa. Inheritance is not limited to one level. A subclass can be a superclass of other classes, forming an inheritance hierarchy. Consider the example shown in Figure 1.13. Inheritance is very powerful, and if it is used properly, we can develop 1.4 Inheritance 23 1. What is the difference between a constant and a variable? 2. Draw an object diagram of a Person object with the three instance variables name, age, and gender. Account Savings Checking Figure 1.12 A superclass Account and its subclasses Savings and Checking. inheritance superclass and subclass wu23399_ch01.qxd 12/12/06 17:24 Page 23
- 54. complex programs very efficiently and elegantly. The flip side of using a very pow- erful tool is that if we do not use it correctly, we could end up in a far worse situation than if we did not use it. We will be seeing many examples of inheritance through- out this book. In Chapter 2, for example, we will introduce many classes that come with the Java system. Most of these classes are defined using inheritance. We will provide an in-depth discussion of inheritance and related topics in Chapter 13. 24 Chapter 1 Introduction to Object-Oriented Programming and Software Development Student Law Doctoral Masters Graduate Undergraduate Commuting Resident Figure 1.13 An example of inheritance hierarchy among different types of students. 1. If Class A inherits from Class B, which is a superclass? Which is a subclass? 2. Draw a diagram that shows Class A is inheriting from Class B. 3. What are the other names for superclass and subclass? 4. If we have Animal, Insect, and Mammal classes, which one will be a superclass? 5. Model different types of vehicles, using inheritance. Include Vehicle, Automobile, Motorcycle, Sports Car, Sedan, and Bicycle. 1.5 Software Engineering and Software Life Cycle When we say computer programming, we are referring not only to writing Java commands, but also to a whole process of software development. Knowing a pro- gramming language alone is not enough to become a proficient software developer. wu23399_ch01.qxd 12/12/06 17:24 Page 24
- 55. Other documents randomly have different content
- 56. Anaxagoras made no distinction between νοῦς and ψυχή. Compare Plato, Kratylus, p. 400 A. 161 Anaxag. Fr. 8, and Schaubach’s Comm. p. 112-116. “Mens erat id, quod movebat molem homœomeriarum: hâc ratione, per hunc motum à mente excitatum, secretio facta est.… Materiæ autem propriæ insunt vires: proprio suo pondere hæc, quæ mentis vi mota et secreta sunt, feruntur in eum locum, quo nunc sunt.” Compare Alexand. Aphrod. ap. Scholia ad Aristot. Physic. ii. p. 194, a. (Schol. p. 348 a. Brandis); Marbach, Lehrbuch der Gesch. Philos. s. 54, note 2, p. 82; Preller, Hist. Phil. ex Font. Loc. Contexta, s. 53, with his comment. 162 Plato, Phædo, c. 107, 108, p. 98; Plato, De Legg. xii. p. 967 B; Aristot. Metaphys. A. 4, p. 985, b. 18; Plato, Timæus, 34 A. 88 E. 163 Aristoph. Nub. 380, 828. αἰθέριος Δῖνος — Δῖνος βασιλεύει, τὸν Δί’ ἐξεληλακώς — the sting of which applies to Anaxagoras and his doctrines. Anaxagoras δίνους τινὰς ἀνοήτους ἀναζωγραφῶν, σὺν τῇ τοῦ νοῦ ἀπραξίᾳ καὶ ἀνοίᾳ (Clemens. Alexandrin. Stromat. ii. p. 365). To move (in the active sense, i.e. to cause movement in) and to know, are the two attributes of the Anaxagorean Νοῦς (Aristotel. De Animâ, i. 2, p. 405, a. 18).
- 57. Plato and Aristotle blame Anaxagoras for deserting his own theory. This we learn from Plato and Aristotle, who blame Anaxagoras for inconsistency in deserting his own hypothesis, and in invoking explanations from physical agencies, to the neglect of Nous and its supposed optimising purposes. But Anaxagoras, as far as we can judge by his remaining fragments, seems not to have committed any such inconsistency. He did not proclaim his Nous to be a powerful extra-cosmical Architect, like the Demiurgus of Plato — nor an intra-cosmical, immanent, undeliberating instinct (such as Aristotle calls Nature), tending towards the production and renewal of regular forms and conjunctions, yet operating along with other agencies which produced concomitants irregular, unpredictable, often even obstructive and monstrous. Anaxagoras appears to conceive his Nous as one among numerous other real agents in Nature, material like the rest, yet differing from the rest as being powerful, simple, and pure from all mixture,164 as being endued with universal cognizance, as being the earliest to act in point of time, and as furnishing the primary condition to the activity of the rest by setting on foot the cosmical rotation. The Homœomeries are coeternal with, if not anterior to, Nous. They have laws and properties of their own, which they follow, when once liberated, without waiting for the dictation of Nous. What they do is known by, but not ordered by, Nous.165 It is therefore no inconsistency in Anaxagoras that he assigns to mind one distinct and peculiar agency, but nothing more; and that when trying to explain the variety of phenomena he makes reference to other physical agencies, as the case seems to require.166 164 Anaxagoras, Fr. 8, p. 100, Schaub. ἐστὶ γὰρ λεπτότατόν τε πάντων χρημάτων, c.
- 58. Astronomy and physics of Anaxagoras. This means, not that νοῦς was unextended or immaterial, but that it was thinner or more subtle than either fire or air. Herakleitus regarded τὸ περιέχον as λογικὸν καὶ φρενῆρες. Diogenes of Apollonia considered air as endued with cognition, and as imparting cognition by being inhaled. Compare Plutarch, De Placit. Philos. iv. 3. I cannot think, with Brücker (Hist. Philosop. part ii. b. ii. De Sectâ Ionicâ, p. 504, ed. 2nd), and with Tennemann, Ges. Ph. i. 8, p. 312, that Anaxagoras was “primus qui Dei ideam inter Græcos à materialitate quasi purificavit,” c. I agree rather with Zeller (Philos. der Griech. i. p. 680-683, ed. 2nd), that the Anaxagorean Nous is not conceived as having either immateriality or personality. 165 Simplikius, in Physic. Aristot. p. 73. καὶ Ἀναξαγόρας δὲ τὸν νοῦν ἐάσας, ὥς φησιν Εὔδημος, καὶ αὐτοματίζων τὰ πολλὰ συνίστησιν. 166 Diogen. Laert. ii. 8. Νοῦν … ἀρχὴν κινήσεως. Brücker, Hist. Philos. ut supra. “Scilicet, semel inducto in materiam à mente motu, sufficere putavit Anaxagoras, juxta leges naturæ motûsque, rerum ortum describere.” In describing the formation of the Kosmos, Anaxagoras supposed that, as a consequence of the rotation initiated by mind, the primitive chaos broke up. “The Dense, Wet, Cold, Dark, Heavy, came together into the place where now Earth is: Hot, Dry, Bare, Light, Bright, departed to the exterior region of the revolving Æther.”167 In such separation each followed its spontaneous and
- 59. inherent tendency. Water was disengaged from air and clouds, earth from water: earth was still farther consolidated into stones by cold.168 Earth remained stationary in the centre, while fire and air were borne round it by the force and violence of the rotatory movement. The celestial bodies — Sun, Moon, and Stars — were solid bodies analogous to the earth, either caught originally in the whirl of the rotatory movement, or torn from the substance of the earth and carried away into the outer region of rotation.169 They were rendered hot and luminous by the fiery fluid in the rapid whirl of which they were hurried along. The Sun was a stone thus made red-hot, larger than Peloponnesus: the Moon was of earthy matter, nearer to the Earth, deriving its light from the Sun, and including not merely plains and mountains, but also cities and inhabitants.170 Of the planetary movements, apart from the diurnal rotation of the celestial sphere, Anaxagoras took no notice.171 He explained the periodical changes in the apparent course of the sun and moon by resistances which they encountered, the former from accumulated and condensed air, the latter from the cold.172 Like Anaximenes and Demokritus, Anaxagoras conceived the Earth as flat, round in the surface, and not deep, resting on and supported by the air beneath it. Originally (he thought) the earth was horizontal, with the axis of celestial rotation perpendicular, and the north pole at the zenith, so that this rotation was then lateral, like that of a dome or roof; it was moreover equable and unchanging with reference to every part of the plane of the earth’s upper surface, and distributed light and heat equally to every part. But after a certain time the Earth tilted over of its own accord to the south, thus lowering its southern half, raising the northern half, and causing the celestial rotation to appear oblique.173 167 Anaxag. Fr. 19, p. 131, Schaub.; compare Fr. 6, p. 97; Diogen. Laert. ii. 8.
- 60. His geology, meteorology, physiology. 168 Anaxag. Fr. 20, p. 133, Schau. 169 See the curious passage in Plutarch, Lysander 12, and Plato, Legg. xii. p. 967 B; Diogen. Laert. ii. 12; Plutarch, Placit. Philos. ii. 13. 170 Plato, Kratylus, p. 409 A; Plato, Apol. Sok. c. 14; Xenophon, Memorab. iv. 7. 171 Schaubach, ad Anax. Fr. p. 165. 172 Plutarch, Placit. Philosoph. ii. 23. 173 Diogenes Laert. ii. 9. τὰ δ’ ἄστρα κατ’ ἀρχὰς θολοειδῶς ἐνεχθῆναι, ὥστε κατὰ κορυφὴν τῆς γῆς τὸν ἀεὶ φαινόμενον εἶναι πόλον, ὕστερον δὲ τὴν (γῆν) ἔγκλισιν λαβεῖν. Plutarch, Placit. Phil. ii. 8. Besides these doctrines respecting the great cosmical bodies, Anaxagoras gave explanations of many among the striking phenomena in geology and meteorology — the sea, rivers, earthquakes, hurricanes, hail, snow, c.174 He treated also of animals and plants — their primary origin, and the manner of their propagation.175 He thought that animals were originally produced by the hot and moist earth; but that being once produced, the breeds were continued by propagation. The seeds of plants he supposed to have been originally contained in the air, from whence they fell down to the warm and moist earth, where they took root and sprung up.176 He believed that all plants, as well as all animals, had a certain measure of intelligence and sentiment, differing not in kind but only in degree from the intelligence and sentiment of men; whose superiority of intelligence was determined, to a great extent, by their possession of hands.177 He explained sensation by the action of unlike upon unlike (contrary to
- 61. Empedokles, who referred it to the action of like upon like),178 applying this doctrine to the explanation of the five senses separately. But he pronounced the senses to be sadly obscure and insufficient as means of knowledge. Apparently, however, he did not discard their testimony, nor assume any other means of knowledge independent of it, but supposed a concomitant and controlling effect of intelligence as indispensable to compare and judge between the facts of sense when they appeared contradictory.179 On this point, however, it is difficult to make out his opinions. 174 See Schaubach, ad Anax. Fr. p. 174-181. Among the points to which Anaxagoras addressed himself was the annual inundation of the Nile, which he ascribed to the melting of the snows in Æthiopia, in the higher regions of the river’s course. — Diodor. i. 38. Herodotus notices this opinion (ii. 22), calling it plausible, but false, yet without naming any one as its author. Compare Euripides, Helen. 3. 175 Aristotel. De Generat. Animal. iii. 6, iv. 1. 176 Theophrastus, Hist. Plant. iii. 2; Diogen. Laert. ii. 9; Aristot. De Plantis, i. 2. 177 Aristot. De Plantis, i. 1; Aristot. Part. Animal. iv. 10. 178 Theophrastus, De Sensu, sect. 1 — sect. 27-30. This difference followed naturally from the opinions of the two philosophers on the nature of the soul or mind. Anaxagoras supposed it peculiar in itself, and dissimilar to the Homœomeries without. Empedokles conceived it as a compound of the four elements, analogous to all that was without: hence man knew each exterior element by
- 62. its like within himself — earth by earth, water by water, c. 179 Anaxag. Fr. 19, Schaub.; Sextus Empiric. adv. Mathem. vii. 91-140; Cicero, Academ. i. 12. Anaxagoras remarked that the contrast between black and white might be made imperceptible to sense by a succession of numerous intermediate colours very finely graduated. He is said to have affirmed that snow was really black, notwithstanding that it appeared white to our senses: since water was black, and snow was only frozen water (Cicero, Academ. iv. 31; Sext. Empir. Pyrrhon. Hypotyp. i. 33). “Anaxagoras non modo id ita esse (sc. albam nivem esse) negabat, sed sibi, quia sciret aquam nigram esse, unde illa concreta esset, albam ipsam esse ne videri quidem.” Whether Anaxagoras ever affirmed that snow did not appear to him white, may reasonably be doubted: his real affirmation probably was, that snow, though it appeared white, was not really white. And this affirmation depended upon the line which he drew between the fact of sense, the phenomenal, the relative, on one side — and the substratum, the real, the absolute, on the other. Most philosophers recognise a distinction between the two; but the line between the two has been drawn in very different directions. Anaxagoras assumed as his substratum, real, or absolute, the Homœomeries — numerous primordial varieties of matter, each with its inherent qualities. Among these varieties he reckoned water, but he did not reckon snow. He also considered that water was really and absolutely black or dark (the Homeric μέλαν ὕδωρ) — that blackness was among its primary qualities. Water, when
- 63. The doctrines of Anaxagoras were regarded as offensive and impious. consolidated into snow, was so disguised as to produce upon the spectator the appearance of whiteness; but it did not really lose, nor could it lose, its inherent colour. A negro covered with white paint, and therefore looking white, is still really black: a wheel painted with the seven prismatic colours, and made to revolve rapidly, will look white, but it is still really septi-coloured: i.e. the state of rapid revolution would be considered as an exceptional state, not natural to it. Compare Plato, Lysis, c. 32, p. 217 D. Anaxagoras, residing at Athens and intimately connected with Perikles, incurred not only unpopularity, but even legal prosecution, by the tenor of his philosophical opinions, especially those on astronomy. To Greeks who believed in Helios and Selênê as not merely living beings but Deities, his declaration that the Sun was a luminous and fiery stone, and the Moon an earthy mass, appeared alike absurd and impious. Such was the judgment of Sokrates, Plato, and Xenophon, as well as of Aristophanes and the general Athenian public.180 Anaxagoras was threatened with indictment for blasphemy, so that Perikles was compelled to send him away from Athens.
- 64. Diogenes of Apollonia recognises one primordial element. 180 Plato, Apol. So. c. 14; Xenoph. Memor. iv. 7. That physical enquiries into the nature of things, and attempts to substitute scientific theories in place of the personal agency of the Gods, were repugnant to the religious feelings of the Greeks, has been already remarked.181 Yet most of the other contemporary philosophers must have been open to this reproach, not less than Anaxagoras; and we learn that the Apolloniate Diogenes left Athens from the same cause. If others escaped the like prosecution which fell upon Anaxagoras, we may probably ascribe this fact to the state of political party at Athens, and to the intimacy of the latter with Perikles. The numerous political enemies of that great man might fairly hope to discredit him in the public mind — at the very least to vex and embarrass him — by procuring the trial and condemnation of Anaxagoras. Against other philosophers, even when propounding doctrines not less obnoxious respecting the celestial bodies, there was not the same collateral motive to stimulate the aggressive hostility of individuals. 181 Plutarch, Nikias, 23. Contemporary with Anaxagoras — yet somewhat younger, as far as we can judge, upon doubtful evidence — lived the philosopher Diogenes, a native of Apollonia in Krete. Of his life we know nothing except that he taught during some time at Athens, which city he was forced to quit on the same ground as Anaxagoras. Accusations of impiety were either brought or threatened against him:182 physical philosophy being offensive generally to the received religious sentiment, which
- 65. was specially awakened and appealed to by the political opponents of Perikles. 182 Diogen. Laert. ix. 52. The danger incurred by Diogenes the Apolloniate at Athens is well authenticated, on the evidence of Demetrius the Phalerean, who had good means of knowing. And the fact may probably be referred to some time after the year B.C. 440, when Athens was at the height of her power and of her attraction for foreign visitors — when the visits of philosophers to the city had been multiplied by the countenance of Perikles — and when the political rivals of that great man had set the fashion of assailing them in order to injure him. This seems to me one probable reason for determining the chronology of the Apolloniate Diogenes: another is, that his description of the veins in the human body is so minute and detailed as to betoken an advanced period of philosophy between B.C. 440-410. See the point discussed in Panzerbieter, Fragment. Diogen. Apoll. c. 12-18 (Leipsic, 1830). Simplikius (ad Aristot. Phys. fol. 6 A) describes Diogenes as having been σχεδὸν νεώτατος in the series of physical theorists. Diogenes the Apolloniate, the latest in the series of Ionic philosophers or physiologists, adopted, with modifications and enlargements, the fundamental tenet of Anaximenes. There was but one primordial element — and that element was air. He laid it down as indisputable that all the different objects in this Kosmos must be at the bottom one and the same thing: unless this were the fact,
- 66. Air was the primordial, universal element. they would not act upon each other, nor mix together, nor do good and harm to each other, as we see that they do. Plants would not grow out of the earth, nor would animals live and grow by nutrition, unless there existed as a basis this universal sameness of nature. No one thing therefore has a peculiar nature of its own: there is in all the same nature, but very changeable and diversified.183 183 Diogen. Ap. Fragm. ii. c. 29 Panzerb.; Theophrastus, De Sensu, s. 39. εἰ γὰρ τὰ ἐν τῷδε τῷ κόσμῳ ἐόντα νῦν γῆ καὶ ὕδωρ καὶ τἄλλα, ὅσα φαινεται ἐν τῷδε τῷ κόσμῳ ἐόντα, εἰ τουτέων τι ἦν τὸ ἕτερον τοῦ ἑτέρου ἕτερον ἐὸν τῇ ἰδίῃ φύσει, καὶ μὴ τὸ αὐτὸ ἐὸν μετέπιπτε πολλαχῶς καὶ ἡτεροιοῦτο· οὐδαμῆ οὔτε μίσγεσθαι ἀλλήλοις ἠδύνατο οὔτε ὠφέλησις τῷ ἑτέρῳ οὔτε βλάβη, c. Aristotle approves this fundamental tenet of Diogenes, the conclusion that there must be one common Something out of which all things came — ἐξ ἑνὸς ἅπαντα (Gen. et Corrupt. i. 6-7, p. 322, a. 14), inferred from the fact that they acted upon each other. Now the fundamental substance, common to all, was air. Air was infinite, eternal, powerful; it was, besides, full of intelligence and knowledge. This latter property Diogenes proved by the succession of climatic and atmospheric phenomena of winter and summer, night and day, rain, wind, and fine weather. All these successions were disposed in the best possible manner by the air: which could not have laid out things in such regular order and measure, unless it had been endowed with intelligence. Moreover,
- 67. Air possessed numerous and diverse properties; was eminently modifiable. air was the source of life, soul, and intelligence, to men and animals: who inhaled all these by respiration, and lost all of them as soon as they ceased to respire.184 184 Diog. Apoll. Fr. iv.-vi. c. 36-42, Panz. — Οὐ γὰρ ἂν οὕτω δέδασθαι οἷόν τε ἦν ἄνευ νοήσιος, ὥστε πάντων μέτρα ἔχειν, χειμῶνός τε καὶ θέρεος και νυκτὸς καὶ ἡμέρης καὶ ὑετῶν καὶ ἀνέμων καὶ εὐδιῶν. καὶ τὰ ἄλλα εἴ τις βούλεται ἐννοέεσθαι, εὕρισκοι ἂν οὕτω διακείμενα, ὡς ἀνυστὸν κάλλιστα. Ἔτι δε πρὸς τούτοις καὶ τάδε μεγάλα σημεῖα· ἄνθρωπος γὰρ καὶ τὰ ἄλλα ζῶα ἀναπνέοντα ζώει τῷ ἀέρι. Καὶ τοῦτο αὐτοῖς καὶ ψυχή ἐστι καὶ νόησις —— — Καὶ μοὶ δοκέει τὸ τὴν νόησιν ἔχον εἶναι ὁ ἀὴρ καλεόμενος ὑπὸ τῶν ἀνθρώπων, c. Schleiermacher has an instructive commentary upon these fragments of the Apolloniate Diogenes (Vermischte Schriften, vol. ii. p. 157-162; Ueber Diogenes von Apollonia). Air, life-giving and intelligent, existed everywhere, formed the essence of everything, comprehended and governed everything. Nothing in nature could be without it: yet at the same time all things in nature partook of it in a different manner.185 For it was distinguished by great diversity of properties and by many gradations of intelligence. It was hotter or colder — moister or drier — denser or rarer — more or less active and movable — exhibiting differences of colour and taste. All these diversities were found in objects, though all at the bottom
- 68. Physiology of Diogenes — his description of the veins in the human body. were air. Reason and intelligence resided in the warm air. So also to all animals as well as to men, the common source of vitality, whereby they lived, saw, heard, and understood, was air; hotter than the atmosphere generally, though much colder than that near the sun.186 Nevertheless, in spite of this common characteristic, the air was in other respects so indefinitely modifiable, that animals were of all degrees of diversity, in form, habits, and intelligence. Men were doubtless more alike among themselves: yet no two of them could be found exactly alike, furnished with the same dose of aerial heat or vitality. All other things, animate and inanimate, were generated and perished, beginning from air and ending in air: which alone continued immortal and indestructible.187 185 Diog. Ap. Fr. vi. καὶ ἐστι μηδὲ ἓν ὅ, τι μὴ μετέχει τούτου (air). Μετέχει δὲ οὐδὲ ἓν ὁμοίως τὸ ἕτερον τῷ ἑτέρῳ· ἀλλὰ πολλοὶ τρόποὶ καὶ αὐτοὺ τοῦ ἀέρος καὶ τῆς νοήσιός εἰσιν. Aristotel. De Animâ, i. 2, p. 405, a. 21. Διογένης δ’, ὥσπερ καὶ ἑτεροί τινες, ἀέρα [ὑπέλαβε τὴν ψυχήν], c. 186 Diog. Ap. Fr. vi. καὶ πάντων ζώων δὴ ἡ ψυχὴ τὸ αὐτό ἐστιν, ἀὴρ θερμότερος μὲν τοῦ ἔξω ἐν ᾧ ἐσμέν, τοῦ μέντοι παρὰ τῷ ἡελίῳ πολλὸν ψυχρότερος. 187 Diogen. Apoll. Fr. v. ch. 38, Panz. The intelligence of men and animals, very unequal in character and degree, was imbibed by respiration, the inspired air passing by means of the veins and along the blood into all parts of the body. Of the veins Diogenes gave a description remarkable for its minuteness of detail,
- 69. in an age when philosophers dwelt almost exclusively in loose general analogies.188 He conceived the principal seat of intelligence in man to be in the thoracic cavity, or in the ventricle of the heart, where a quantity of air was accumulated ready for distribution.189 The warm and dry air concentrated round the brain, and reached by veins from the organs of sense, was the centre of sensation. Taste was explained by the soft and porous nature of the tongue, and by the number of veins communicating with it. The juices of sapid bodies were sucked up by it as by a sponge: the odorous stream of air penetrated from without through the nostrils: both were thus brought into conjunction with the sympathising cerebral air. To this air also the image impressed upon the eye was transmitted, thereby causing vision:190 while pulsations and vibrations of the air without, entering through the ears and impinging upon the same centre, generated the sensation of sound. If the veins connecting the eye with the brain were inflamed, no visual sensation could take place;191 moreover if our minds or attention were absorbed in other things, we were often altogether insensible to sensations either of sight or of sound: which proved that the central air within us was the real seat of sensation.192 Thought and intelligence, as well as sensation, was an attribute of the same central air within us, depending especially upon its purity, dryness, and heat, and impeded or deadened by moisture or cold. Both children and animals had less intelligence than men: because they had more moisture in their bodies, so that the veins were choked up, and the air could not get along them freely to all parts. Plants had no intelligence; having no apertures or ducts whereby the air could pervade their internal structure. Our sensations were pleasurable when there was much air mingled with the blood, so as to lighten the flow of it, and to carry it
- 70. easily to all parts: they were painful when there was little air, and when the blood was torpid and thick.193 188 Diogen. Apoll. Fr. vii. ch. 48, Panz. The description of the veins given by Diogenes is preserved in Aristotel. Hist. Animal, iii. 2: yet seemingly only in a defective abstract, for Theophrastus alludes to various opinions of Diogenes on the veins, which are not contained in Aristotle. See Philippson, Ὕλη ἀνθρωπίνη, p. 203. 189 Plutarch, Placit. Philos. iv. 5. Ἐν τῇ ἀρτηριακῇ κοιλίᾳ τῆς καρδίας, ἥτις ἐστὶ καὶ πνευματική. See Panzerbieter’s commentary upon these words, which are not very clear (c. 50), nor easy to reconcile with the description given by Diogenes himself of the veins. 190 Plutarch, Placit. Philosoph. iv. 18. Theophrast. De Sensu, s. 39-41-43. Κριτικώτατον δὲ ἡδονῆς τὴν γλῶτταν· ἁπαλώτατον γὰρ εἶναι καὶ μανὸν καὶ τὰς φλέβας ἁπάσας ἀνήκειν εἰς αὐτήν. 191 Plutarch, Placit. Philosoph. iv. 16; Theophrastus, De Sensu, s. 40. 192 Theophrast. De Sensu, s. 42. Ὅτι δὲ ὁ ἐντὸς ἀὴρ αἰσθάνεται, μικρὸν ὢν μόριον τοῦ θεοῦ, σημεῖον εἶναι, ὅτι πολλάκις πρὸς ἄλλα τὸν νοῦν ἔχοντες οὔθ’ ὁρῶμεν οὔτ’ ἀκούομεν. The same opinion — that sensation, like thought, is a mental process, depending on physical conditions — is ascribed to Strato (the disciple and successor of Theophrastus) by Porphyry, De Abstinentiâ, iii. 21. Στράτωνος τοῦ φυσικοῦ λόγος
- 71. Kosmology and meteorology. ἐστὶν ἀποδεικνύων, ὡς οὐδὲ αἰσθάνεσθαι το παράπαν ἄνευ τοῦ νοεῖν ὑπάρχει. καὶ γὰρ γράμματα πολλάκις ἐπιπορευομένους τῇ ὄψει καὶ λόγοι προσπίπτοντες τῇ ἀκοῇ διαλανθάνουσιν ἡμᾶς καὶ διαφεύγουσι πρὸς ἑτέρους τὸν νοῦν ἔχοντας — ᾗ καὶ λέλεκται, νοῦς ὁρῆ καὶ νοῦς ἀκούει, τἄλλα κωφὰ καὶ τυφλά. The expression ascribed to Diogenes by Theophrastus — ὁ ἐντὸς ἀὴρ, μικρὸν ὢν μόριον τ ο ῦ θ ε ο ῦ — is so printed by Philippson; but the word θεοῦ seems not well avouched as to the text, and Schneider prints θυμοῦ. It is not impossible that Diogenes may have called the air God, without departing from his physical theory; but this requires proof. 193 Theophrastus, De Sensu, s. 43-46; Plutarch, Placit. Philos. v. 20. That moisture is the cause of dulness, and that the dry soul is the best and most intelligent — is cited among the doctrines of Herakleitus, with whom Diogenes of Apollonia is often in harmony. Αὔη ψυχὴ σοφωτάτη καὶ ἀρίστη. See Schleiermach. Herakleitos, sect. 59-64. The structure of the Kosmos Diogenes supposed to have been effected by portions of the infinite air, taking upon them new qualities and undergoing various transformations. Some air, becoming cold, dense, and heavy, sunk down to the centre, and there remained stationary as earth and water: while the hotter, rarer, and lighter air ascended and formed the heavens, assuming through the intelligence included in it a rapid
- 72. rotatory movement round the earth, and shaping itself into sun, moon, and stars, which were light and porous bodies like pumice stone. The heat of this celestial matter acted continually upon the earth and water beneath, so that the earth became comparatively drier, and the water was more and more drawn up as vapour, to serve for nourishment to the heavenly bodies. The stars also acted as breathing-holes to the Kosmos, supplying the heated celestial mass with fresh air from the infinite mass without.194 Like Anaxagoras, Diogenes conceived the figure of the earth as flat and round, like a drum; and the rotation of the heavens as lateral, with the axis perpendicular to the surface of the earth, and the north pole always at the zenith. This he supposed to have been the original arrangement; but after a certain time, the earth tilted over spontaneously towards the south — the northern half was elevated and the southern half depressed — so that the north pole was no longer at the zenith, and the axis of rotation of the heavens became apparently oblique.195 He thought, moreover, that the existing Kosmos was only of temporary duration; that it would perish and be succeeded by future analogous systems, generated from the same common substance of the infinite and indestructible air.196 Respecting animal generation — and to some extent respecting meteorological phenomena197 — Diogenes also propounded several opinions, which are imperfectly known, but which appear to have resembled those of Anaxagoras. 194 Plutarch ap. Eusebium Præp. Evang. i. 8; Aristotel. De Animâ, i. 2; Diogen. Laert. ix. 53. Διογένης κισσηροειδῆ τὰ ἄστρα, διαπνοίας δὲ αὐτὰ νομίζει τοῦ κόσμου, εἶναι δὲ διάπυρα· συμπεριφέρεσθαι δὲ τοῖς φανεροῖς ἄστροις ἀφανεῖς λίθους καὶ παρ’ αὐτὸ τοῦτ’ ἀνωνύμους· πίπτοντα δὲ πολλάκις ἐπὶ τῆς γῆς
- 73. Leukippus and Demokritus — Atomic theory. σβέννυσθαι· καθάπερ τὸν ἐν Αἰγὸς ποταμοῖς πυρωδῶς κατενεχθέντα ἀ σ τ έ ρ α πέτρινον. This remarkable anticipation of modern astronomy — the recognition of aerolithes as a class of non-luminous earthy bodies revolving round the sun, but occasionally coming within the sphere of the earth’s attraction, becoming luminous in our atmosphere, falling on the earth, and there being extinguished — is noticed by Alex. von Humboldt in his Kosmos, vol. i. p. 98-104, Eng. trans. He says — “The opinion of Diogenes of Apollonia entirely accords with that of the present day,” p. 110. The charm and value of that interesting book is greatly enhanced by his frequent reference to the ancient points of view on astronomical subjects. 195 Plutarch, Placit. Philos. ii. 8; Panzerbieter ad Diog. Ap. c. 76-78; Schaubach ad Anaxagor. Fr. p. 175. 196 Plut. Ap. Euseb. Præp. Evang. i. 8. 197 Preller, Hist. Philosoph. Græc.-Rom. ex Font. Loc. Contexta, sect. 68. Preller thinks that Diogenes employed his chief attention “in animantium naturâ ex aeris principio repetendâ”; and that he was less full “in cognitione τῶν μετεώρων”. But the fragments scarcely justify this. Nearly contemporary with Anaxagoras and Empedokles, two other enquirers propounded a new physical theory very different from those already noticed — usually known under the name of the atomic theory. This Atomic theory, though
- 74. Long life, varied travels, and numerous compositions of Demokritus. originating with the Eleate Leukippus, obtained celebrity chiefly from his pupil Demokritus of Abdera, its expositor and improver. Demokritus (born seemingly in B.C. 460, and reported to have reached extreme old age) was nine years younger than Sokrates, thirty-three years older than Plato, and forty years younger than Anaxagoras.198 The age of Leukippus is not known, but he can hardly have been much younger than Anaxagoras. 198 Diogen. Laert. ix. 41. See the chronology of Demokritus discussed in Mullach, Frag. Dem. p. 12-25; and in Zeller, Phil. der Griech., vol. i. p. 576-681, 2nd edit. The statement of Apollodorus as to the date of his birth, appears more trustworthy than the earlier date assigned by Thrasyllus (B.C. 470). Demokritus declared himself to be forty years younger than Anaxagoras. Of Leukippus we know nothing: of Demokritus, very little — yet enough to exhibit a life, like that of Anaxagoras, consecrated to philosophical investigation, and neglectful not merely of politics, but even of inherited patrimony.199 His attention was chiefly turned towards the study of Nature, with conceptions less vague, and a more enlarged observation of facts, than any of his contemporaries had ever bestowed. He was enabled to boast that no one had surpassed him in extent of travelling over foreign lands, in intelligent research and converse with enlightened natives, or in following out the geometrical relations of lines.200 He spent several years in visiting Egypt, Asia Minor, and Persia. His writings were numerous, and on many different subjects, including ethics, as well
- 75. as physics, astronomy, and anthropology. None of them have been preserved. But we read, even from critics like Dionysius of Halikarnassus and Cicero, that they were composed in an impressive and semi-poetical style, not unworthy to be mentioned in analogy with Plato; while in range and diversity of subjects they are hardly inferior to Aristotle.201 199 Dionys. ix. 36-39. 200 Demokrit. Fragm. 6, p. 238, ed. Mullach. Compare ib. p. 41; Diogen. Laert. ix. 35; Strabo, xv. p. 703. Pliny, Hist. Natur. “Democritus — vitam inter experimenta consumpsit,” c. 201 Cicero, Orat. c. 20; Dionys. De Comp. Verbor. c. 24; Sextus Empir. adv. Mathem. vii. 265. Δημόκριτος, ὁ τῇ Διὸς φώνῃ παρεικαζόμενος, c. Diogenes (ix. 46-48) enumerates the titles of the treatises of Demokritus, as edited in the days of Tiberius by the rhetor Thrasyllus: who distributed them into tetralogies, as he also distributed the dialogues of Plato. It was probably the charm of style, common to Demokritus with Plato, which induced the rhetor thus to edit them both. In regard to scope and spirit of philosophy, the difference between the two was so marked, that Plato is said to have had a positive antipathy to the works of Demokritus, and a desire to burn them (Aristoxenus ap. Diog. Laert. ix. 40). It could hardly be from congeniality of doctrine that the same editor attached himself to both. It has been
- 76. Relation between the theory of Demokritus and that of Parmenides. remarked that Plato never once names Demokritus, while Aristotle cites him very frequently, sometimes with marked praise. The theory of Leukippus and Demokritus (we have no means of distinguishing the two) appears to have grown out the Eleatic theory.202 Parmenides the Eleate (as I have already stated) in distinguishing Ens, the self-existent, real, or absolute, on one side — from the phenomenal and relative on the other — conceived the former in such a way that its connection with the latter was dissolved. The real and absolute, according to him, was One, extended, enduring, continuous, unchangeable, immovable: the conception of Ens included these affirmations, and at the same time excluded peremptorily Non-Ens, or the contrary of Ens. Now the plural, unextended, transient, discontinuous, changeable, and moving, implied a mixture of Ens and Non-Ens, or a partial transition from one to the other. Hence (since Non-Ens was inadmissible) such plurality, c., could not belong to the real or absolute (ultra- phenomenal), and could only be affirmed as phenomenal or relative. In the latter sense, Parmenides did affirm it, and even tried to explain it: he explained the phenomenal facts from phenomenal assumptions, apart from and independent of the absolute. While thus breaking down the bridge between the phenomenal on one side and the absolute on the other, he nevertheless recognised each in a sphere of its own. 202 Simplikius, in Aristotel. Physic. fol. 7 A. Λεύκιππος … κοινωνήσας Παρμενίδῃ τῆς φιλοσοφίας, οὐ τὴν αὐτὴν ἐβάδισε Παρμενίδῃ καὶ Ξενοφάνει περὶ τῶν
- 77. Demokritean theory — Atoms — Plena and Vacua — Ens and Non-Ens. ὄντων δόξαν, ἀλλ’, ὡς δοκεῖ, τὴν ἐναντίαν. Aristotel. De Gener. et Corr. i. 8, p. 251, a. 31. Diogen. Laert. ix. 30. This bridge the atomists undertook to re-establish. They admitted that Ens could not really change — that there could be no real generation, or destruction — no transformation of qualities — no transition of many into one, or of one into many. But they denied the unity and continuity and immobility of Ens: they affirmed that it was essentially discontinuous, plural, and moving. They distinguished the extended, which Parmenides had treated as an Unum continuum, into extension with body, and extension without body: into plenum and vacuum, matter and space. They conceived themselves to have thus found positive meanings both for Ens and Non-Ens. That which Parmenides called Non-Ens or nothing, was in their judgment the vacuum; not less self-existent than that which he called Something. They established their point by showing that Ens, thus interpreted, would become reconcilable to the phenomena of sense: which latter they assumed as their basis to start from. Assuming motion as a phenomenal fact, obvious and incontestable, they asserted that it could not even appear to be a fact, without supposing vacuum as well as body to be real: and the proof that both of them were real was, that only in this manner could sense and reason be reconciled. Farther, they proved the existence of a vacuum by appeal to direct physical observation, which showed that bodies were porous, compressible, and capable of receiving into themselves new matter in the way of nutrition. Instead of the Parmenidean Ens, one and continuous, we have a Demokritean Ens, essentially many and discontinuous: plena and vacua, spaces full and spaces empty, being
- 78. infinitely intermingled.203 There existed atoms innumerable, each one in itself essentially a plenum, admitting no vacant space within it, and therefore indivisible as well as indestructible: but each severed from the rest by surrounding vacant space. The atom could undergo no change: but by means of the empty space around, it could freely move. Each atom was too small to be visible: yet all atoms were not equally small; there were fundamental differences between them in figure and magnitude: and they had no other qualities except figure and magnitude. As no atom could be divided into two, so no two atoms could merge into one. Yet though two or more atoms could not so merge together as to lose their real separate individuality, they might nevertheless come into such close approximation as to appear one, and to act on our senses as a phenomenal combination manifesting itself by new sensible properties.204 203 It is chiefly in the eighth chapter of the treatise De Gener. et Corr. (i. 8) that Aristotle traces the doctrine of Leukippus as having grown out of that of the Eleates. Λεύκιππος δ’ ἔχειν ᾠήθη λόγους, οἵτινες πρὸς τὴν αἴσθησιν ὁμολογούμενα λέγοντες οὐκ ἀναιρήσουσιν οὔτε γένεσιν οὔτε φθορὰν οὔτε κίνησιν καὶ τὸ πλῆθος τῶν ὄντων, c. Compare also Aristotel. De Cœlo, iii. 4, p. 303, a. 6; Metaphys. A. 4, p. 985, b. 5; Physic. iv. 6: λέγουσι δὲ (Demokritus, c., in proving a vacuum) ἓν μὲν ὅτι ἡ κίνησις ἡ κατὰ τόπον οὐκ ἂν εἴη, ο ὐ γ ὰ ρ ἂ ν δ ο κ ε ῖ ν εἶναι κίνησιν εἰ μὴ εἴη κενόν· τὸ γὰρ πλῆρες ἀδύνατον εἶναι δέξασθαί τι, c.
- 79. Plutarch adv. Kolot. p. 1108. Οἷς οὐδ’ ὄναρ ἐντυχὼν ὁ Κολώτης, ἐσφάλη περὶ λέξιν τοῦ ἀνδρὸς (Demokritus) ἐν ᾖ διορίζεται, μὴ μᾶλλον τὸ δὲν, ἢ τὸ μηδὲν εἶναι· δὲν μὲν ὀνομάζων τὸ σῶμα μηδὲν δὲ τὸ κενόν, ὡς καὶ τούτου φύσιν τινὰ καὶ ὑπόστασιν ἰδίαν ἔχοντος. The affirmation of Demokritus — That Nothing existed, just as much as Something — appears a paradox which we must probably understand as implying that he here adopted, for the sake of argument, the language of the Eleates, his opponents. They called the vacuum Nothing, but Demokritus did not so call it. If (said Demokritus) you call vacuum Nothing, then I say that Nothing exists as well as Something. The direct observations by which Demokritus showed the existence of a vacuum were — 1. A vessel with ashes in it will hold as much water as if it were empty: hence we know that there are pores in the ashes, into which the water is received. 2. Wine can be compressed in skins. 3. The growth of organised bodies proves that they have pores, through which new matter in the form of nourishment is admitted. (Aristot. Physic. iv. 6, p. 213, b.) Besides this, Demokritus set forth motion as an indisputable fact, ascertained by the evidence of sense: and affirmed that motion was impossible, except on the assumption that vacuum existed. Melissus, the disciple of Parmenides, inverted the
- 80. Primordial atoms differed only in magnitude, figure, position, and arrangement — they had no qualities, but their movements and combinations generated qualities. reasoning, in arguing against the reality of motion. If it be real (he said), then there must exist a vacuum: but no vacuum does or can exist: therefore there is no real motion. (Aristot. Physic. iv. 6.) Since Demokritus started from these facts of sense, as the base of his hypothesis of atoms and vacua, so Aristotle (Gen. et Corr. i. 2; De Animâ, i. 2) might reasonably say that he took sensible appearances as truth. But we find Demokritus also describing reason as an improvement and enlightenment of sense, and complaining how little of truth was discoverable by man. See Mullach, Demokritus (pp. 414, 415). Compare Philippson — Ὗλη ἀνθρωπίνη — Berlin, 1831. 204 Aristotel. Gen. et Corr. i. 8, p. 325, a. 25, τὰ πρῶτα μεγέθη τὰ ἀδιαίρετα στερεά. Diogen. Laert. ix. 44; Plutarch, adv. Koloten, p. 1110 seq. Zeller, Philos. der Griech., vol. i. p. 583-588, ed. 2nd; Aristotel. Metaphys. Z. 13, p. 1039, a. 10, ἀδύνατον εἶναί φησι Δημόκριτος ἐκ δύο ἓν ᾒ ἐξ ἑνὸς δύο γενέσθαι· τὰ γὰρ μεγέθη τὰ ἄτομα τὰς οὐσίας ποιεῖ. The bridge, broken down by Parmenides, between the real and the phenomenal world, was thus in theory re-established. For the real world, as described by Demokritus, differed entirely from the sameness and barrenness of the Parmenidean Ens, and presented sufficient movement and
- 81. variety to supply a basis of explanatory hypothesis, accommodated to more or less of the varieties in the phenomenal world. In respect of quality, indeed, all the atoms were alike, not less than all the vacua: such likeness was (according to Demokritus) the condition of their being able to act upon each other, or to combine as phenomenal aggregates.205 But in respect to quantity or magnitude as well as in respect to figure, they differed very greatly: moreover, besides all these diversities, the ordination and position of each atom with regard to the rest were variable in every way. As all objects of sense were atomic compounds, so, from such fundamental differences — partly in the constituent atoms themselves, partly in the manner of their arrangement when thrown into combination — arose all the diverse qualities and manifestations of the compounds. When atoms passed into new combination, then there was generation of a new substance: when they passed out of an old combination there was destruction: when the atoms remained the same, but were merely arranged anew in order and relative position, then the phenomenon was simply change. Hence all qualities and manifestations of such compounds were not original, but derivative: they had no “nature of their own,” or law peculiar to them, but followed from the atomic composition of the body to which they belonged. They were not real and absolute, like the magnitude and figure of the constituent atoms, but phenomenal and relative — i.e. they were powers of acting upon correlative organs of sentient beings, and nullities in the absence of such organs.206 Such were the colour, sonorousness, taste, smell, heat, cold, c., of the bodies around us: they were relative, implying correlative percipients. Moreover they were not merely relative, but perpetually fluctuating; since the compounds were frequently changing either in arrangement or in diversity of atoms, and every such atomic change,
- 82. even to a small extent, caused it to work differently upon our organs.207 205 Aristotel. Gener. et Corr. i. 7, p. 323, b. 12. It was the opinion of Demokritus, that there could be no action except where agent and patient were alike. Φησὶ γὰρ τὸ αὐτὸ καὶ ὅμοιον εἶναι τό τε ποιοῦν καὶ τὸ πάσχον· οὐ γὰρ ἐγχωρεῖν τὰ ἕτερα καὶ διαφέροντα πάσχειν ὑπ’ ἀλλήλων· ἀλλὰ κἂν ἕτερα ὄντα ποιῇ τι εἰς ἄλληλα, οὐχ ᾗ ἕτερα, ἀλλ’ ᾗ ταὐτόν τι ὑπάρχει, ταύτῃ τοῦτο συμβαίνειν αὐτοῖς. Many contemporary philosophers affirmed distinctly the opposite. Τὸ ὅμοιον ὑπὸ τοῦ ὁμοίου πᾶν ἀπαθές, c. Diogenes the Apolloniate agreed on this point generally with Demokritus; see above, p. 61, note 1. The facility with which these philosophers laid down general maxims is constantly observable. 206 Aristot. Gen. et Corr. i. 2, p. 316, a. 1; Theophrast. De Sensu, s. 63, 64. Περὶ μὲν οὖν βαρέος καὶ κούφου καὶ σκληροῦ καὶ μαλακοῦ ἐν τούτοις ἀφορίζει· τῶν δὲ ἄλλων αἰσθητῶν οὐδενὸς εἶναι φύσιν, ἀλλὰ πάντα πάθη τῆς αἰσθήσεως ἀλλοιουμένης, ἐξ ἧς γίνεσθαι τὴν φαντασίαν, c. Stobæus, Eclog. Physic. i. c. 16. Φύσιν μὲν μηδὲν εἶναι χρῶμα, τὰ μὲν γὰρ στοιχεῖα ἄποια, τά τε μεστὰ καὶ τὸ κενόν· τὰ δ’ ἐξ αὐτῶν συγκρίματα κέχρῶσθαι διαταγῇ τε καὶ ῥυθμῷ καὶ προτροπῇ, c. Demokritus restricted the term Φύσις — Nature — to the primordial atoms and vacua (Simplikius ad Aristot.
- 83. Combinations of atoms — generating different qualities in the compounds. Physic. p. 310 A.). 207 Aristotel. Gener. et Corr. i. 2, p. 315, b. 10. Ὥστε ταῖς μεταβολαῖς τοῦ συγκειμένου τὸ αὐτὸ ἐναντίον δοκεῖν ἄλλῳ καὶ ἄλλῳ, καὶ μετακινεῖσθαι μικροῦ ἐμμιγνυμένου, κ α ὶ ὅ λ ω ς ἕ τ ε ρ ο ν φ α ί ν ε σ θ α ι ἑ ν ὸ ς μ ε τ α κ ι ν η θ έ ν τ ο ς . Among the various properties of bodies, however, there were two which Demokritus recognised as not merely relative to the observer, but also as absolute and belonging to the body in itself. These were weight and hardness — primary qualities (to use the phraseology of Locke and Reid), as contrasted with the secondary qualities of colour, taste, and the like. Weight, or tendency downward, belonged (according to Demokritus) to each individual atom separately, in proportion to its magnitude: the specific gravity of all atoms was supposed to be equal. In compound bodies one body was heavier than another, in proportion as its bulk was more filled with atoms and less with vacant space.208 The hardness and softness of bodies Demokritus explained by the peculiar size and peculiar junction of their component atoms. Thus, comparing lead with iron, the former is heavier and softer, the latter is lighter and harder. Bulk for bulk, the lead contained a larger proportion of solid, and a smaller proportion of interstices, than the iron: hence it was heavier. But its structure was equable throughout; it had a greater multitude of minute atoms diffused through its bulk, equally close to and coherent with each other on every side, but not more close and coherent on one side than on another. The structure of the iron, on the contrary, was unequal and irregular, including larger spaces of vacuum in one part,
- 84. Welcome to our website – the perfect destination for book lovers and knowledge seekers. We believe that every book holds a new world, offering opportunities for learning, discovery, and personal growth. That’s why we are dedicated to bringing you a diverse collection of books, ranging from classic literature and specialized publications to self-development guides and children's books. More than just a book-buying platform, we strive to be a bridge connecting you with timeless cultural and intellectual values. With an elegant, user-friendly interface and a smart search system, you can quickly find the books that best suit your interests. Additionally, our special promotions and home delivery services help you save time and fully enjoy the joy of reading. Join us on a journey of knowledge exploration, passion nurturing, and personal growth every day! ebookbell.com






















![Preface xix
Object-Oriented Approach
We take the object-first approach to teaching object-oriented programming with emphasis
on proper object-oriented design.The concept of objects is clearly illustrated from the very
first sample program.
/*
Chapter 2 Sample Program: Displaying a Window
File: Ch2Sample1.java
*/
import javax.swing.*;
class Ch2Sample1 {
public static void main(String[] args) {
JFrame myWindow;
myWindow = new JFrame();
myWindow.setSize(300, 200);
myWindow.setTitle(My First Java Program);
myWindow.setVisible(true);
}
}
Dorm
Door
Resident
User module
Dorm Resident
A helper class
provided to us
A class we
implement
One or more classes
we implement
Administrative
module
Figure 8.8 Program diagrams for the user and administrative modules.Notice the same Dorm and
Resident classes are used in both programs.User and administrative modules will include one or more
classes (at least one is programmer-defined).
Good practices on object-
oriented design are
discussed throughout
the book and illustrated
through numerous
sample programs.
wu23399_fm.qxd 1/10/07 11:55 Page xix](https://image.slidesharecdn.com/1202222-250529161441-16ad6ed4/85/A-Comprehensive-Introduction-To-Objectoriented-Programming-With-Java-C-Thomas-Wu-23-320.jpg)















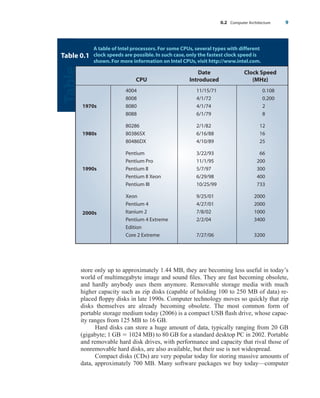




![5. What is the maximum decimal number you can represent in 4 bits? 16 bits?
N bits?
6. If a computer has 128 MB of RAM, how many bytes are there?
7. How do high-level programming languages differ from low-level
programming languages?
8. Consider a hypothetical programming language called Kona. Using Kona,
you can write a program to compute and print out the sum of 20 integers
entered by the user:
let sum = 0;
repeat 20 times [
let X = next input;
add X to sum;
]
printout sum;
Is Kona a high-level language? Why or why not?
14 Chapter 0 Introduction to Computers and Programming Languages
wu23392_ch00.qxd 12/12/06 17:23 Page 14](https://image.slidesharecdn.com/1202222-250529161441-16ad6ed4/85/A-Comprehensive-Introduction-To-Objectoriented-Programming-With-Java-C-Thomas-Wu-44-320.jpg)























![Physiology of Diogenes —
his description of the veins
in the human body.
were air. Reason and intelligence resided in the warm air. So also to
all animals as well as to men, the common source of vitality,
whereby they lived, saw, heard, and understood, was air; hotter
than the atmosphere generally, though much colder than that near
the sun.186 Nevertheless, in spite of this common characteristic, the
air was in other respects so indefinitely modifiable, that animals
were of all degrees of diversity, in form, habits, and intelligence. Men
were doubtless more alike among themselves: yet no two of them
could be found exactly alike, furnished with the same dose of aerial
heat or vitality. All other things, animate and inanimate, were
generated and perished, beginning from air and ending in air: which
alone continued immortal and indestructible.187
185 Diog. Ap. Fr. vi. καὶ ἐστι μηδὲ ἓν ὅ, τι μὴ μετέχει
τούτου (air). Μετέχει δὲ οὐδὲ ἓν ὁμοίως τὸ ἕτερον τῷ
ἑτέρῳ· ἀλλὰ πολλοὶ τρόποὶ καὶ αὐτοὺ τοῦ ἀέρος καὶ
τῆς νοήσιός εἰσιν.
Aristotel. De Animâ, i. 2, p. 405, a. 21. Διογένης δ’,
ὥσπερ καὶ ἑτεροί τινες, ἀέρα [ὑπέλαβε τὴν ψυχήν], c.
186 Diog. Ap. Fr. vi. καὶ πάντων ζώων δὴ ἡ ψυχὴ τὸ
αὐτό ἐστιν, ἀὴρ θερμότερος μὲν τοῦ ἔξω ἐν ᾧ ἐσμέν,
τοῦ μέντοι παρὰ τῷ ἡελίῳ πολλὸν ψυχρότερος.
187 Diogen. Apoll. Fr. v. ch. 38, Panz.
The intelligence of men and animals,
very unequal in character and degree,
was imbibed by respiration, the
inspired air passing by means of the
veins and along the blood into all parts of the body. Of the veins
Diogenes gave a description remarkable for its minuteness of detail,](https://image.slidesharecdn.com/1202222-250529161441-16ad6ed4/85/A-Comprehensive-Introduction-To-Objectoriented-Programming-With-Java-C-Thomas-Wu-68-320.jpg)















