algorithm_6dynamic_programming.pdf
- 1. Iris Hui-Ru Jiang Fall 2014 CHAPTER 6 DYNAMIC PROGRAMMING IRIS H.-R. JIANG Outline ¨ Content: ¤ Weighted interval scheduling: a recursive procedure ¤ Principles of dynamic programming (DP) n Memoization or iteration over subproblems ¤ Example: maze routing ¤ Example: Fibonacci sequence ¤ Subset sums and Knapsacks: adding a variable ¤ Shortest paths in a graph ¤ Example: traveling salesman problem ¨ Reading: ¤ Chapter 6 Dynamic programming 2 IRIS H.-R. JIANG Recap Divide-and-Conquer (D&C) ¨ Divide and conquer: ¤ (Divide) Break down a problem into two or more sub-problems of the same (or related) type ¤ (Conquer) Recursively solve each sub-problems and solve them directly if simple enough ¤ (Combine) Combine these solutions to the sub-problems to give a solution to the original problem ¨ Correctness: proved by mathematical induction ¨ Complexity: determined by solving recurrence relations Dynamic programming 3 IRIS H.-R. JIANG Dynamic Programming (DP) ¨ Dynamic “programming” came from the term “mathematical programming” ¤ Typically on optimization problems (a problem with an objective) ¤ Inventor: Richard E. Bellman, 1953 ¨ Basic idea: One implicitly explores the space of all possible solutions by ¤ Carefully decomposing things into a series of subproblems ¤ Building up correct solutions to larger and larger subproblems ¨ Can you smell the D&C flavor? However, DP is another story! ¤ DP does not exam all possible solutions explicitly ¤ Be aware of the condition to apply DP!! Dynamic programming 4 http://www.wu.ac.at/usr/h99c/h9951826/bellman_dynprog.pdf http://en.wikipedia.org/wiki/Dynamic_programming
- 2. Iris Hui-Ru Jiang Fall 2014 CHAPTER 6 DYNAMIC PROGRAMMING IRIS H.-R. JIANG Outline ¨ Content: ¤ Weighted interval scheduling: a recursive procedure ¤ Principles of dynamic programming (DP) n Memoization or iteration over subproblems ¤ Example: maze routing ¤ Example: Fibonacci sequence ¤ Subset sums and Knapsacks: adding a variable ¤ Shortest paths in a graph ¤ Example: traveling salesman problem ¨ Reading: ¤ Chapter 6 Dynamic programming 2 IRIS H.-R. JIANG Recap Divide-and-Conquer (D&C) ¨ Divide and conquer: ¤ (Divide) Break down a problem into two or more sub-problems of the same (or related) type ¤ (Conquer) Recursively solve each sub-problems and solve them directly if simple enough ¤ (Combine) Combine these solutions to the sub-problems to give a solution to the original problem ¨ Correctness: proved by mathematical induction ¨ Complexity: determined by solving recurrence relations Dynamic programming 3 IRIS H.-R. JIANG Dynamic Programming (DP) ¨ Dynamic “programming” came from the term “mathematical programming” ¤ Typically on optimization problems (a problem with an objective) ¤ Inventor: Richard E. Bellman, 1953 ¨ Basic idea: One implicitly explores the space of all possible solutions by ¤ Carefully decomposing things into a series of subproblems ¤ Building up correct solutions to larger and larger subproblems ¨ Can you smell the D&C flavor? However, DP is another story! ¤ DP does not exam all possible solutions explicitly ¤ Be aware of the condition to apply DP!! Dynamic programming 4 http://www.wu.ac.at/usr/h99c/h9951826/bellman_dynprog.pdf http://en.wikipedia.org/wiki/Dynamic_programming
- 3. Iris Hui-Ru Jiang Fall 2014 CHAPTER 6 DYNAMIC PROGRAMMING IRIS H.-R. JIANG Outline ¨ Content: ¤ Weighted interval scheduling: a recursive procedure ¤ Principles of dynamic programming (DP) n Memoization or iteration over subproblems ¤ Example: maze routing ¤ Example: Fibonacci sequence ¤ Subset sums and Knapsacks: adding a variable ¤ Shortest paths in a graph ¤ Example: traveling salesman problem ¨ Reading: ¤ Chapter 6 Dynamic programming 2 IRIS H.-R. JIANG Recap Divide-and-Conquer (D&C) ¨ Divide and conquer: ¤ (Divide) Break down a problem into two or more sub-problems of the same (or related) type ¤ (Conquer) Recursively solve each sub-problems and solve them directly if simple enough ¤ (Combine) Combine these solutions to the sub-problems to give a solution to the original problem ¨ Correctness: proved by mathematical induction ¨ Complexity: determined by solving recurrence relations Dynamic programming 3 IRIS H.-R. JIANG Dynamic Programming (DP) ¨ Dynamic “programming” came from the term “mathematical programming” ¤ Typically on optimization problems (a problem with an objective) ¤ Inventor: Richard E. Bellman, 1953 ¨ Basic idea: One implicitly explores the space of all possible solutions by ¤ Carefully decomposing things into a series of subproblems ¤ Building up correct solutions to larger and larger subproblems ¨ Can you smell the D&C flavor? However, DP is another story! ¤ DP does not exam all possible solutions explicitly ¤ Be aware of the condition to apply DP!! Dynamic programming 4 http://www.wu.ac.at/usr/h99c/h9951826/bellman_dynprog.pdf http://en.wikipedia.org/wiki/Dynamic_programming
- 4. Iris Hui-Ru Jiang Fall 2014 CHAPTER 6 DYNAMIC PROGRAMMING IRIS H.-R. JIANG Outline ¨ Content: ¤ Weighted interval scheduling: a recursive procedure ¤ Principles of dynamic programming (DP) n Memoization or iteration over subproblems ¤ Example: maze routing ¤ Example: Fibonacci sequence ¤ Subset sums and Knapsacks: adding a variable ¤ Shortest paths in a graph ¤ Example: traveling salesman problem ¨ Reading: ¤ Chapter 6 Dynamic programming 2 IRIS H.-R. JIANG Recap Divide-and-Conquer (D&C) ¨ Divide and conquer: ¤ (Divide) Break down a problem into two or more sub-problems of the same (or related) type ¤ (Conquer) Recursively solve each sub-problems and solve them directly if simple enough ¤ (Combine) Combine these solutions to the sub-problems to give a solution to the original problem ¨ Correctness: proved by mathematical induction ¨ Complexity: determined by solving recurrence relations Dynamic programming 3 IRIS H.-R. JIANG Dynamic Programming (DP) ¨ Dynamic “programming” came from the term “mathematical programming” ¤ Typically on optimization problems (a problem with an objective) ¤ Inventor: Richard E. Bellman, 1953 ¨ Basic idea: One implicitly explores the space of all possible solutions by ¤ Carefully decomposing things into a series of subproblems ¤ Building up correct solutions to larger and larger subproblems ¨ Can you smell the D&C flavor? However, DP is another story! ¤ DP does not exam all possible solutions explicitly ¤ Be aware of the condition to apply DP!! Dynamic programming 4 http://www.wu.ac.at/usr/h99c/h9951826/bellman_dynprog.pdf http://en.wikipedia.org/wiki/Dynamic_programming
- 5. Thinking in an inductive way Weighted Interval Scheduling 5 Dynamic programming IRIS H.-R. JIANG Weighted Interval Scheduling ¨ Given: A set of n intervals with start/finish times, weights (values) ¤ Interval i: [si, fi), vi, 1 £ i £ n ¨ Find: A subset S of mutually compatible intervals with maximum total values Dynamic programming 6 Time 0 1 2 3 4 5 6 7 8 9 10 11 20 11 16 13 23 12 20 26 16 26 Maximum weighted compatible set {26, 16} IRIS H.-R. JIANG Greedy? ¨ The greedy algorithm of unit-weighted (vi = 1, 1 £ i £ n) intervals no longer works! ¤ Sort intervals in ascending order of finish times ¤ Pick up if compatible; otherwise, discard it ¨ Q: What if variable values? Dynamic programming 7 Time 0 1 2 3 4 5 6 7 8 9 10 11 1 1 3 1 1 3 IRIS H.-R. JIANG Designing a Recursive Algorithm (1/3) ¨ In the induction perspective, a recursive algorithm tries to compose the overall solution using the solutions of sub- problems (problems of smaller sizes) ¨ First attempt: Induction on time? ¤ Granularity? Dynamic programming 8 1 2 2 4 4 7 t t’ 1
- 6. Thinking in an inductive way Weighted Interval Scheduling 5 Dynamic programming IRIS H.-R. JIANG Weighted Interval Scheduling ¨ Given: A set of n intervals with start/finish times, weights (values) ¤ Interval i: [si, fi), vi, 1 £ i £ n ¨ Find: A subset S of mutually compatible intervals with maximum total values Dynamic programming 6 Time 0 1 2 3 4 5 6 7 8 9 10 11 20 11 16 13 23 12 20 26 16 26 Maximum weighted compatible set {26, 16} IRIS H.-R. JIANG Greedy? ¨ The greedy algorithm of unit-weighted (vi = 1, 1 £ i £ n) intervals no longer works! ¤ Sort intervals in ascending order of finish times ¤ Pick up if compatible; otherwise, discard it ¨ Q: What if variable values? Dynamic programming 7 Time 0 1 2 3 4 5 6 7 8 9 10 11 1 1 3 1 1 3 IRIS H.-R. JIANG Designing a Recursive Algorithm (1/3) ¨ In the induction perspective, a recursive algorithm tries to compose the overall solution using the solutions of sub- problems (problems of smaller sizes) ¨ First attempt: Induction on time? ¤ Granularity? Dynamic programming 8 1 2 2 4 4 7 t t’ 1
- 7. Thinking in an inductive way Weighted Interval Scheduling 5 Dynamic programming IRIS H.-R. JIANG Weighted Interval Scheduling ¨ Given: A set of n intervals with start/finish times, weights (values) ¤ Interval i: [si, fi), vi, 1 £ i £ n ¨ Find: A subset S of mutually compatible intervals with maximum total values Dynamic programming 6 Time 0 1 2 3 4 5 6 7 8 9 10 11 20 11 16 13 23 12 20 26 16 26 Maximum weighted compatible set {26, 16} IRIS H.-R. JIANG Greedy? ¨ The greedy algorithm of unit-weighted (vi = 1, 1 £ i £ n) intervals no longer works! ¤ Sort intervals in ascending order of finish times ¤ Pick up if compatible; otherwise, discard it ¨ Q: What if variable values? Dynamic programming 7 Time 0 1 2 3 4 5 6 7 8 9 10 11 1 1 3 1 1 3 IRIS H.-R. JIANG Designing a Recursive Algorithm (1/3) ¨ In the induction perspective, a recursive algorithm tries to compose the overall solution using the solutions of sub- problems (problems of smaller sizes) ¨ First attempt: Induction on time? ¤ Granularity? Dynamic programming 8 1 2 2 4 4 7 t t’ 1
- 8. Thinking in an inductive way Weighted Interval Scheduling 5 Dynamic programming IRIS H.-R. JIANG Weighted Interval Scheduling ¨ Given: A set of n intervals with start/finish times, weights (values) ¤ Interval i: [si, fi), vi, 1 £ i £ n ¨ Find: A subset S of mutually compatible intervals with maximum total values Dynamic programming 6 Time 0 1 2 3 4 5 6 7 8 9 10 11 20 11 16 13 23 12 20 26 16 26 Maximum weighted compatible set {26, 16} IRIS H.-R. JIANG Greedy? ¨ The greedy algorithm of unit-weighted (vi = 1, 1 £ i £ n) intervals no longer works! ¤ Sort intervals in ascending order of finish times ¤ Pick up if compatible; otherwise, discard it ¨ Q: What if variable values? Dynamic programming 7 Time 0 1 2 3 4 5 6 7 8 9 10 11 1 1 3 1 1 3 IRIS H.-R. JIANG Designing a Recursive Algorithm (1/3) ¨ In the induction perspective, a recursive algorithm tries to compose the overall solution using the solutions of sub- problems (problems of smaller sizes) ¨ First attempt: Induction on time? ¤ Granularity? Dynamic programming 8 1 2 2 4 4 7 t t’ 1
- 9. IRIS H.-R. JIANG Designing a Recursive Algorithm (2/3) ¨ Second attempt: Induction on interval index ¤ First of all, sort intervals in ascending order of finish times ¤ In fact, this is also a trick for DP ¨ p(j) is the largest index i < j s.t. intervals i and j are disjoint ¤ p(j) = 0 if no request i < j is disjoint from j Dynamic programming 9 1 2 2 4 4 7 p(1) = 0 p(2) = 0 p(3) = 1 p(4) = 0 p(5) = 3 p(6) = 3 1 2 3 4 5 6 p(2) = 0 p(6) = 3 4 1 4 IRIS H.-R. JIANG Designing a Recursive Algorithm (3/3) ¨ Oj = the optimal solution for intervals 1, …, j ¨ OPT(j) = the value of the optimal solution for intervals 1, …, j ¤ e.g., O6 = ? Include interval 6 or not? n Þ O6 = {6, O3} or O5 n OPT(6) = max{{v6+OPT(3)}, OPT(5)} ¤ OPT(j) = max{{vj+OPT(p(j))}, OPT(j-1)} Dynamic programming 10 1 2 2 4 4 7 p(1) = 0 p(2) = 0 p(3) = 1 p(4) = 0 p(5) = 3 p(6) = 3 1 2 3 4 5 6 1 IRIS H.-R. JIANG Direct Implementation Dynamic programming 11 // Preprocessing: // 1. Sort intervals by finish times: f1 £ f2 £ ... £ fn // 2. Compute p(1), p(2), …, p(n) Compute-Opt(j) 1. if (j = 0) then return 0 2. else return max{{vj+Compute-Opt(p(j))}, Compute-Opt(j-1)} OPT(j) = max{{vj+OPT(p(j))}, OPT(j-1)} 5 4 3 1 2 1 3 2 1 1 6 3 2 1 1 The tree of calls widens very quickly due to recursive branching! 1 2 2 4 4 7 p(1) = 0 p(2) = 0 p(3) = 1 p(4) = 0 p(5) = 3 p(6) = 3 IRIS H.-R. JIANG Memoization: Top-Down ¨ The tree of calls widens very quickly due to recursive branching! ¤ e.g., exponential running time when p(j) = j – 2 for all j ¨ Q: What’s wrong? A: Redundant calls! ¨ Q: How to eliminate this redundancy? ¨ A: Store the value for future! (memoization) Dynamic programming 12 5 4 3 1 2 1 3 2 1 1 6 3 2 1 1 3 1 2 1 3 2 1 1 3 2 1 1 M-Compute-Opt(j) 1. if (j = 0) then return 0 2. else if (M[j] is not empty) then return M[j] 3. else return M[j] = max{{vj+M-Compute-Opt(p(j))}, M-Compute-Opt(j-1)} Running time: O(n) How to report the optimal solution O? 5 4 3 2 1 6
- 10. IRIS H.-R. JIANG Designing a Recursive Algorithm (2/3) ¨ Second attempt: Induction on interval index ¤ First of all, sort intervals in ascending order of finish times ¤ In fact, this is also a trick for DP ¨ p(j) is the largest index i < j s.t. intervals i and j are disjoint ¤ p(j) = 0 if no request i < j is disjoint from j Dynamic programming 9 1 2 2 4 4 7 p(1) = 0 p(2) = 0 p(3) = 1 p(4) = 0 p(5) = 3 p(6) = 3 1 2 3 4 5 6 p(2) = 0 p(6) = 3 4 1 4 IRIS H.-R. JIANG Designing a Recursive Algorithm (3/3) ¨ Oj = the optimal solution for intervals 1, …, j ¨ OPT(j) = the value of the optimal solution for intervals 1, …, j ¤ e.g., O6 = ? Include interval 6 or not? n Þ O6 = {6, O3} or O5 n OPT(6) = max{{v6+OPT(3)}, OPT(5)} ¤ OPT(j) = max{{vj+OPT(p(j))}, OPT(j-1)} Dynamic programming 10 1 2 2 4 4 7 p(1) = 0 p(2) = 0 p(3) = 1 p(4) = 0 p(5) = 3 p(6) = 3 1 2 3 4 5 6 1 IRIS H.-R. JIANG Direct Implementation Dynamic programming 11 // Preprocessing: // 1. Sort intervals by finish times: f1 £ f2 £ ... £ fn // 2. Compute p(1), p(2), …, p(n) Compute-Opt(j) 1. if (j = 0) then return 0 2. else return max{{vj+Compute-Opt(p(j))}, Compute-Opt(j-1)} OPT(j) = max{{vj+OPT(p(j))}, OPT(j-1)} 5 4 3 1 2 1 3 2 1 1 6 3 2 1 1 The tree of calls widens very quickly due to recursive branching! 1 2 2 4 4 7 p(1) = 0 p(2) = 0 p(3) = 1 p(4) = 0 p(5) = 3 p(6) = 3 IRIS H.-R. JIANG Memoization: Top-Down ¨ The tree of calls widens very quickly due to recursive branching! ¤ e.g., exponential running time when p(j) = j – 2 for all j ¨ Q: What’s wrong? A: Redundant calls! ¨ Q: How to eliminate this redundancy? ¨ A: Store the value for future! (memoization) Dynamic programming 12 5 4 3 1 2 1 3 2 1 1 6 3 2 1 1 3 1 2 1 3 2 1 1 3 2 1 1 M-Compute-Opt(j) 1. if (j = 0) then return 0 2. else if (M[j] is not empty) then return M[j] 3. else return M[j] = max{{vj+M-Compute-Opt(p(j))}, M-Compute-Opt(j-1)} Running time: O(n) How to report the optimal solution O? 5 4 3 2 1 6
- 11. IRIS H.-R. JIANG Designing a Recursive Algorithm (2/3) ¨ Second attempt: Induction on interval index ¤ First of all, sort intervals in ascending order of finish times ¤ In fact, this is also a trick for DP ¨ p(j) is the largest index i < j s.t. intervals i and j are disjoint ¤ p(j) = 0 if no request i < j is disjoint from j Dynamic programming 9 1 2 2 4 4 7 p(1) = 0 p(2) = 0 p(3) = 1 p(4) = 0 p(5) = 3 p(6) = 3 1 2 3 4 5 6 p(2) = 0 p(6) = 3 4 1 4 IRIS H.-R. JIANG Designing a Recursive Algorithm (3/3) ¨ Oj = the optimal solution for intervals 1, …, j ¨ OPT(j) = the value of the optimal solution for intervals 1, …, j ¤ e.g., O6 = ? Include interval 6 or not? n Þ O6 = {6, O3} or O5 n OPT(6) = max{{v6+OPT(3)}, OPT(5)} ¤ OPT(j) = max{{vj+OPT(p(j))}, OPT(j-1)} Dynamic programming 10 1 2 2 4 4 7 p(1) = 0 p(2) = 0 p(3) = 1 p(4) = 0 p(5) = 3 p(6) = 3 1 2 3 4 5 6 1 IRIS H.-R. JIANG Direct Implementation Dynamic programming 11 // Preprocessing: // 1. Sort intervals by finish times: f1 £ f2 £ ... £ fn // 2. Compute p(1), p(2), …, p(n) Compute-Opt(j) 1. if (j = 0) then return 0 2. else return max{{vj+Compute-Opt(p(j))}, Compute-Opt(j-1)} OPT(j) = max{{vj+OPT(p(j))}, OPT(j-1)} 5 4 3 1 2 1 3 2 1 1 6 3 2 1 1 The tree of calls widens very quickly due to recursive branching! 1 2 2 4 4 7 p(1) = 0 p(2) = 0 p(3) = 1 p(4) = 0 p(5) = 3 p(6) = 3 IRIS H.-R. JIANG Memoization: Top-Down ¨ The tree of calls widens very quickly due to recursive branching! ¤ e.g., exponential running time when p(j) = j – 2 for all j ¨ Q: What’s wrong? A: Redundant calls! ¨ Q: How to eliminate this redundancy? ¨ A: Store the value for future! (memoization) Dynamic programming 12 5 4 3 1 2 1 3 2 1 1 6 3 2 1 1 3 1 2 1 3 2 1 1 3 2 1 1 M-Compute-Opt(j) 1. if (j = 0) then return 0 2. else if (M[j] is not empty) then return M[j] 3. else return M[j] = max{{vj+M-Compute-Opt(p(j))}, M-Compute-Opt(j-1)} Running time: O(n) How to report the optimal solution O? 5 4 3 2 1 6
- 12. IRIS H.-R. JIANG Designing a Recursive Algorithm (2/3) ¨ Second attempt: Induction on interval index ¤ First of all, sort intervals in ascending order of finish times ¤ In fact, this is also a trick for DP ¨ p(j) is the largest index i < j s.t. intervals i and j are disjoint ¤ p(j) = 0 if no request i < j is disjoint from j Dynamic programming 9 1 2 2 4 4 7 p(1) = 0 p(2) = 0 p(3) = 1 p(4) = 0 p(5) = 3 p(6) = 3 1 2 3 4 5 6 p(2) = 0 p(6) = 3 4 1 4 IRIS H.-R. JIANG Designing a Recursive Algorithm (3/3) ¨ Oj = the optimal solution for intervals 1, …, j ¨ OPT(j) = the value of the optimal solution for intervals 1, …, j ¤ e.g., O6 = ? Include interval 6 or not? n Þ O6 = {6, O3} or O5 n OPT(6) = max{{v6+OPT(3)}, OPT(5)} ¤ OPT(j) = max{{vj+OPT(p(j))}, OPT(j-1)} Dynamic programming 10 1 2 2 4 4 7 p(1) = 0 p(2) = 0 p(3) = 1 p(4) = 0 p(5) = 3 p(6) = 3 1 2 3 4 5 6 1 IRIS H.-R. JIANG Direct Implementation Dynamic programming 11 // Preprocessing: // 1. Sort intervals by finish times: f1 £ f2 £ ... £ fn // 2. Compute p(1), p(2), …, p(n) Compute-Opt(j) 1. if (j = 0) then return 0 2. else return max{{vj+Compute-Opt(p(j))}, Compute-Opt(j-1)} OPT(j) = max{{vj+OPT(p(j))}, OPT(j-1)} 5 4 3 1 2 1 3 2 1 1 6 3 2 1 1 The tree of calls widens very quickly due to recursive branching! 1 2 2 4 4 7 p(1) = 0 p(2) = 0 p(3) = 1 p(4) = 0 p(5) = 3 p(6) = 3 IRIS H.-R. JIANG Memoization: Top-Down ¨ The tree of calls widens very quickly due to recursive branching! ¤ e.g., exponential running time when p(j) = j – 2 for all j ¨ Q: What’s wrong? A: Redundant calls! ¨ Q: How to eliminate this redundancy? ¨ A: Store the value for future! (memoization) Dynamic programming 12 5 4 3 1 2 1 3 2 1 1 6 3 2 1 1 3 1 2 1 3 2 1 1 3 2 1 1 M-Compute-Opt(j) 1. if (j = 0) then return 0 2. else if (M[j] is not empty) then return M[j] 3. else return M[j] = max{{vj+M-Compute-Opt(p(j))}, M-Compute-Opt(j-1)} Running time: O(n) How to report the optimal solution O? 5 4 3 2 1 6
- 13. IRIS H.-R. JIANG Iteration: Bottom-Up ¨ We can also compute the array M[j] by an iterative algorithm. Dynamic programming 13 I-Compute-Opt 1. M[0] = 0 2. for j = 1, 2, .., n do 3. M[j] = max{vj+M[p(j)], M[j-1]} Running time: O(n) 1 2 2 4 4 7 p(1) = 0 p(2) = 0 p(3) = 1 p(4) = 0 p(5) = 3 p(6) = 3 1 2 3 4 5 6 0 2 4 0 2 4 6 0 2 4 6 7 0 2 4 6 7 8 0 2 4 6 7 8 8 M = 0 1 2 3 4 5 0 6 0 2 max{4+0, 2} IRIS H.-R. JIANG Summary: Memoization vs. Iteration ¨ Top-down ¨ An recursive algorithm ¤ Compute only what we need ¨ Bottom-up ¨ An iterative algorithm ¤ Construct solutions from the smallest subproblem to the largest one ¤ Compute every small piece Memoization Iteration 14 Dynamic programming The running time and memory requirement highly depend on the table size Start with the recursive divide-and-conquer algorithm IRIS H.-R. JIANG Keys for Dynamic Programming ¨ Dynamic programming can be used if the problem satisfies the following properties: ¤ There are only a polynomial number of subproblems ¤ The solution to the original problem can be easily computed from the solutions to the subproblems ¤ There is a natural ordering on subproblems from “smallest” to “largest,” together with an easy-to-compute recurrence Dynamic programming 15 5 4 3 1 2 1 3 2 1 1 6 3 2 1 1 3 1 2 1 3 2 1 1 3 2 1 1 5 4 3 2 1 6 IRIS H.-R. JIANG Keys for Dynamic Programming ¨ DP typically is applied to optimization problems. ¨ DP works best on objects that are linearly ordered an cannot be rearranged ¨ Elements of DP ¤ Optimal substructure: an optimal solution contains within its optimal solutions to subproblems. ¤ Overlapping subproblem: a recursive algorithm revisits the same problem over and over again; typically, the total number of distinct subproblems is a polynomial in the input size. Dynamic programming 16 Cormen, Leiserson, Rivest, Stein, Introduction to Algorithms, 2nd Ed., McGraw Hill/MIT Press, 2001 5 4 3 1 2 1 3 2 1 1 6 3 2 1 1 3 1 2 1 3 2 1 1 3 2 1 1 5 4 3 2 1 6 In optimization problems, we are interested in finding a thing which maximizes or minimizes some function.
- 14. IRIS H.-R. JIANG Iteration: Bottom-Up ¨ We can also compute the array M[j] by an iterative algorithm. Dynamic programming 13 I-Compute-Opt 1. M[0] = 0 2. for j = 1, 2, .., n do 3. M[j] = max{vj+M[p(j)], M[j-1]} Running time: O(n) 1 2 2 4 4 7 p(1) = 0 p(2) = 0 p(3) = 1 p(4) = 0 p(5) = 3 p(6) = 3 1 2 3 4 5 6 0 2 4 0 2 4 6 0 2 4 6 7 0 2 4 6 7 8 0 2 4 6 7 8 8 M = 0 1 2 3 4 5 0 6 0 2 max{4+0, 2} IRIS H.-R. JIANG Summary: Memoization vs. Iteration ¨ Top-down ¨ An recursive algorithm ¤ Compute only what we need ¨ Bottom-up ¨ An iterative algorithm ¤ Construct solutions from the smallest subproblem to the largest one ¤ Compute every small piece Memoization Iteration 14 Dynamic programming The running time and memory requirement highly depend on the table size Start with the recursive divide-and-conquer algorithm IRIS H.-R. JIANG Keys for Dynamic Programming ¨ Dynamic programming can be used if the problem satisfies the following properties: ¤ There are only a polynomial number of subproblems ¤ The solution to the original problem can be easily computed from the solutions to the subproblems ¤ There is a natural ordering on subproblems from “smallest” to “largest,” together with an easy-to-compute recurrence Dynamic programming 15 5 4 3 1 2 1 3 2 1 1 6 3 2 1 1 3 1 2 1 3 2 1 1 3 2 1 1 5 4 3 2 1 6 IRIS H.-R. JIANG Keys for Dynamic Programming ¨ DP typically is applied to optimization problems. ¨ DP works best on objects that are linearly ordered an cannot be rearranged ¨ Elements of DP ¤ Optimal substructure: an optimal solution contains within its optimal solutions to subproblems. ¤ Overlapping subproblem: a recursive algorithm revisits the same problem over and over again; typically, the total number of distinct subproblems is a polynomial in the input size. Dynamic programming 16 Cormen, Leiserson, Rivest, Stein, Introduction to Algorithms, 2nd Ed., McGraw Hill/MIT Press, 2001 5 4 3 1 2 1 3 2 1 1 6 3 2 1 1 3 1 2 1 3 2 1 1 3 2 1 1 5 4 3 2 1 6 In optimization problems, we are interested in finding a thing which maximizes or minimizes some function.
- 15. IRIS H.-R. JIANG Iteration: Bottom-Up ¨ We can also compute the array M[j] by an iterative algorithm. Dynamic programming 13 I-Compute-Opt 1. M[0] = 0 2. for j = 1, 2, .., n do 3. M[j] = max{vj+M[p(j)], M[j-1]} Running time: O(n) 1 2 2 4 4 7 p(1) = 0 p(2) = 0 p(3) = 1 p(4) = 0 p(5) = 3 p(6) = 3 1 2 3 4 5 6 0 2 4 0 2 4 6 0 2 4 6 7 0 2 4 6 7 8 0 2 4 6 7 8 8 M = 0 1 2 3 4 5 0 6 0 2 max{4+0, 2} IRIS H.-R. JIANG Summary: Memoization vs. Iteration ¨ Top-down ¨ An recursive algorithm ¤ Compute only what we need ¨ Bottom-up ¨ An iterative algorithm ¤ Construct solutions from the smallest subproblem to the largest one ¤ Compute every small piece Memoization Iteration 14 Dynamic programming The running time and memory requirement highly depend on the table size Start with the recursive divide-and-conquer algorithm IRIS H.-R. JIANG Keys for Dynamic Programming ¨ Dynamic programming can be used if the problem satisfies the following properties: ¤ There are only a polynomial number of subproblems ¤ The solution to the original problem can be easily computed from the solutions to the subproblems ¤ There is a natural ordering on subproblems from “smallest” to “largest,” together with an easy-to-compute recurrence Dynamic programming 15 5 4 3 1 2 1 3 2 1 1 6 3 2 1 1 3 1 2 1 3 2 1 1 3 2 1 1 5 4 3 2 1 6 IRIS H.-R. JIANG Keys for Dynamic Programming ¨ DP typically is applied to optimization problems. ¨ DP works best on objects that are linearly ordered an cannot be rearranged ¨ Elements of DP ¤ Optimal substructure: an optimal solution contains within its optimal solutions to subproblems. ¤ Overlapping subproblem: a recursive algorithm revisits the same problem over and over again; typically, the total number of distinct subproblems is a polynomial in the input size. Dynamic programming 16 Cormen, Leiserson, Rivest, Stein, Introduction to Algorithms, 2nd Ed., McGraw Hill/MIT Press, 2001 5 4 3 1 2 1 3 2 1 1 6 3 2 1 1 3 1 2 1 3 2 1 1 3 2 1 1 5 4 3 2 1 6 In optimization problems, we are interested in finding a thing which maximizes or minimizes some function.
- 16. IRIS H.-R. JIANG Iteration: Bottom-Up ¨ We can also compute the array M[j] by an iterative algorithm. Dynamic programming 13 I-Compute-Opt 1. M[0] = 0 2. for j = 1, 2, .., n do 3. M[j] = max{vj+M[p(j)], M[j-1]} Running time: O(n) 1 2 2 4 4 7 p(1) = 0 p(2) = 0 p(3) = 1 p(4) = 0 p(5) = 3 p(6) = 3 1 2 3 4 5 6 0 2 4 0 2 4 6 0 2 4 6 7 0 2 4 6 7 8 0 2 4 6 7 8 8 M = 0 1 2 3 4 5 0 6 0 2 max{4+0, 2} IRIS H.-R. JIANG Summary: Memoization vs. Iteration ¨ Top-down ¨ An recursive algorithm ¤ Compute only what we need ¨ Bottom-up ¨ An iterative algorithm ¤ Construct solutions from the smallest subproblem to the largest one ¤ Compute every small piece Memoization Iteration 14 Dynamic programming The running time and memory requirement highly depend on the table size Start with the recursive divide-and-conquer algorithm IRIS H.-R. JIANG Keys for Dynamic Programming ¨ Dynamic programming can be used if the problem satisfies the following properties: ¤ There are only a polynomial number of subproblems ¤ The solution to the original problem can be easily computed from the solutions to the subproblems ¤ There is a natural ordering on subproblems from “smallest” to “largest,” together with an easy-to-compute recurrence Dynamic programming 15 5 4 3 1 2 1 3 2 1 1 6 3 2 1 1 3 1 2 1 3 2 1 1 3 2 1 1 5 4 3 2 1 6 IRIS H.-R. JIANG Keys for Dynamic Programming ¨ DP typically is applied to optimization problems. ¨ DP works best on objects that are linearly ordered an cannot be rearranged ¨ Elements of DP ¤ Optimal substructure: an optimal solution contains within its optimal solutions to subproblems. ¤ Overlapping subproblem: a recursive algorithm revisits the same problem over and over again; typically, the total number of distinct subproblems is a polynomial in the input size. Dynamic programming 16 Cormen, Leiserson, Rivest, Stein, Introduction to Algorithms, 2nd Ed., McGraw Hill/MIT Press, 2001 5 4 3 1 2 1 3 2 1 1 6 3 2 1 1 3 1 2 1 3 2 1 1 3 2 1 1 5 4 3 2 1 6 In optimization problems, we are interested in finding a thing which maximizes or minimizes some function.
- 17. IRIS H.-R. JIANG Keys for Dynamic Programming ¨ Standard operation procedure for DP: 1. Formulate the answer as a recurrence relation or recursive algorithm. (Start with divide-and-conquer) 2. Show that the number of different instances of your recurrence is bounded by a polynomial. 3. Specify an order of evaluation for the recurrence so you always have what you need. Dynamic programming 17 5 4 3 1 2 1 3 2 1 1 6 3 2 1 1 3 1 2 1 3 2 1 1 3 2 1 1 5 4 3 2 1 6 Steven Skiena, Analysis of Algorithms lecture notes, Dept. of CS, SUNY Stony Brook IRIS H.-R. JIANG Algorithmic Paradigms ¨ Brute-force (Exhaustive): Examine the entire set of possible solutions explicitly ¤ A victim to show the efficiencies of the following methods ¨ Greedy: Build up a solution incrementally, myopically optimizing some local criterion. ¨ Divide-and-conquer: Break up a problem into two sub- problems, solve each sub-problem independently, and combine solution to sub-problems to form solution to original problem. ¨ Dynamic programming: Break up a problem into a series of overlapping sub-problems, and build up solutions to larger and larger sub-problems. Dynamic programming 18 Appendix: Fibonacci Sequence 19 Dynamic programming IRIS H.-R. JIANG Fibonacci Sequence ¨ Recurrence relation: Fn = Fn-1 + Fn-2, F0=0, F1=1 ¤ e.g., 0, 1, 1, 2, 3, 5, 8, … ¨ Direct implementation: ¤ Recursion! Dynamic programming 20 fib(n) 1. if n £ 1 return n 2. return fib(n ! 1) + fib(n ! 2)
- 18. IRIS H.-R. JIANG Keys for Dynamic Programming ¨ Standard operation procedure for DP: 1. Formulate the answer as a recurrence relation or recursive algorithm. (Start with divide-and-conquer) 2. Show that the number of different instances of your recurrence is bounded by a polynomial. 3. Specify an order of evaluation for the recurrence so you always have what you need. Dynamic programming 17 5 4 3 1 2 1 3 2 1 1 6 3 2 1 1 3 1 2 1 3 2 1 1 3 2 1 1 5 4 3 2 1 6 Steven Skiena, Analysis of Algorithms lecture notes, Dept. of CS, SUNY Stony Brook IRIS H.-R. JIANG Algorithmic Paradigms ¨ Brute-force (Exhaustive): Examine the entire set of possible solutions explicitly ¤ A victim to show the efficiencies of the following methods ¨ Greedy: Build up a solution incrementally, myopically optimizing some local criterion. ¨ Divide-and-conquer: Break up a problem into two sub- problems, solve each sub-problem independently, and combine solution to sub-problems to form solution to original problem. ¨ Dynamic programming: Break up a problem into a series of overlapping sub-problems, and build up solutions to larger and larger sub-problems. Dynamic programming 18 Appendix: Fibonacci Sequence 19 Dynamic programming IRIS H.-R. JIANG Fibonacci Sequence ¨ Recurrence relation: Fn = Fn-1 + Fn-2, F0=0, F1=1 ¤ e.g., 0, 1, 1, 2, 3, 5, 8, … ¨ Direct implementation: ¤ Recursion! Dynamic programming 20 fib(n) 1. if n £ 1 return n 2. return fib(n ! 1) + fib(n ! 2)
- 19. IRIS H.-R. JIANG Keys for Dynamic Programming ¨ Standard operation procedure for DP: 1. Formulate the answer as a recurrence relation or recursive algorithm. (Start with divide-and-conquer) 2. Show that the number of different instances of your recurrence is bounded by a polynomial. 3. Specify an order of evaluation for the recurrence so you always have what you need. Dynamic programming 17 5 4 3 1 2 1 3 2 1 1 6 3 2 1 1 3 1 2 1 3 2 1 1 3 2 1 1 5 4 3 2 1 6 Steven Skiena, Analysis of Algorithms lecture notes, Dept. of CS, SUNY Stony Brook IRIS H.-R. JIANG Algorithmic Paradigms ¨ Brute-force (Exhaustive): Examine the entire set of possible solutions explicitly ¤ A victim to show the efficiencies of the following methods ¨ Greedy: Build up a solution incrementally, myopically optimizing some local criterion. ¨ Divide-and-conquer: Break up a problem into two sub- problems, solve each sub-problem independently, and combine solution to sub-problems to form solution to original problem. ¨ Dynamic programming: Break up a problem into a series of overlapping sub-problems, and build up solutions to larger and larger sub-problems. Dynamic programming 18 Appendix: Fibonacci Sequence 19 Dynamic programming IRIS H.-R. JIANG Fibonacci Sequence ¨ Recurrence relation: Fn = Fn-1 + Fn-2, F0=0, F1=1 ¤ e.g., 0, 1, 1, 2, 3, 5, 8, … ¨ Direct implementation: ¤ Recursion! Dynamic programming 20 fib(n) 1. if n £ 1 return n 2. return fib(n ! 1) + fib(n ! 2)
- 20. IRIS H.-R. JIANG Keys for Dynamic Programming ¨ Standard operation procedure for DP: 1. Formulate the answer as a recurrence relation or recursive algorithm. (Start with divide-and-conquer) 2. Show that the number of different instances of your recurrence is bounded by a polynomial. 3. Specify an order of evaluation for the recurrence so you always have what you need. Dynamic programming 17 5 4 3 1 2 1 3 2 1 1 6 3 2 1 1 3 1 2 1 3 2 1 1 3 2 1 1 5 4 3 2 1 6 Steven Skiena, Analysis of Algorithms lecture notes, Dept. of CS, SUNY Stony Brook IRIS H.-R. JIANG Algorithmic Paradigms ¨ Brute-force (Exhaustive): Examine the entire set of possible solutions explicitly ¤ A victim to show the efficiencies of the following methods ¨ Greedy: Build up a solution incrementally, myopically optimizing some local criterion. ¨ Divide-and-conquer: Break up a problem into two sub- problems, solve each sub-problem independently, and combine solution to sub-problems to form solution to original problem. ¨ Dynamic programming: Break up a problem into a series of overlapping sub-problems, and build up solutions to larger and larger sub-problems. Dynamic programming 18 Appendix: Fibonacci Sequence 19 Dynamic programming IRIS H.-R. JIANG Fibonacci Sequence ¨ Recurrence relation: Fn = Fn-1 + Fn-2, F0=0, F1=1 ¤ e.g., 0, 1, 1, 2, 3, 5, 8, … ¨ Direct implementation: ¤ Recursion! Dynamic programming 20 fib(n) 1. if n £ 1 return n 2. return fib(n ! 1) + fib(n ! 2)
- 21. IRIS H.-R. JIANG What’s Wrong? ¨ What if we call fib(5)? ¤ fib(5) ¤ fib(4) + fib(3) ¤ (fib(3) + fib(2)) + (fib(2) + fib(1)) ¤ ((fib(2) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1)) ¤ (((fib(1) + fib(0)) + fib(1))+(fib(1) + fib(0)))+((fib(1) + fib(0))+fib(1)) ¤ A call tree that calls the function on the same value many different times n fib(2) was calculated three times from scratch n Impractical for large n Dynamic programming 21 fib(n) 1. if n £ 1 return n 2. return fib(n ! 1) + fib(n ! 2) 5 4 3 2 3 2 1 2 1 0 1 0 1 1 0 2 1 0 2 1 0 2 1 0 IRIS H.-R. JIANG Too Many Redundant Calls! ¨ How to remove redundancy? ¤ Prevent repeated calculation Recursion True dependency Dynamic programming 22 5 4 3 2 1 5 4 3 2 3 2 1 2 1 0 1 0 1 1 0 3 2 3 1 2 1 0 1 1 0 2 1 0 2 1 0 2 1 0 IRIS H.-R. JIANG Dynamic Programming -- Memoization ¨ Store the values in a table ¤ Check the table before a recursive call ¤ Top-down! n The control flow is almost the same as the original one Dynamic programming 23 fib(n) 1. Initialize f[0..n] with -1 // -1: unfilled 2. f[0] = 0; f[1] = 1 3. fibonacci(n, f) fibonacci(n, f) 1. If f[n] == -1 then 2. f[n] = fibonacci(n ! 1, f) + fibonacci(n ! 2, f) 3. return f[n] // if f[n] already exists, directly return 5 4 3 2 1 IRIS H.-R. JIANG Dynamic Programming -- Bottom-up? ¨ Store the values in a table ¤ Bottom-up n Compute the values for small problems first ¤ Much like induction Dynamic programming 24 fib(n) 1. initialize f[1..n] with -1 // -1: unfilled 2. f[0] = 0; f[1] = 1 3. for i=2 to n do 4. f[i] = f[i-1]+ f[i-2] 5. return f[n] 5 4 3 2 1
- 22. IRIS H.-R. JIANG What’s Wrong? ¨ What if we call fib(5)? ¤ fib(5) ¤ fib(4) + fib(3) ¤ (fib(3) + fib(2)) + (fib(2) + fib(1)) ¤ ((fib(2) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1)) ¤ (((fib(1) + fib(0)) + fib(1))+(fib(1) + fib(0)))+((fib(1) + fib(0))+fib(1)) ¤ A call tree that calls the function on the same value many different times n fib(2) was calculated three times from scratch n Impractical for large n Dynamic programming 21 fib(n) 1. if n £ 1 return n 2. return fib(n ! 1) + fib(n ! 2) 5 4 3 2 3 2 1 2 1 0 1 0 1 1 0 2 1 0 2 1 0 2 1 0 IRIS H.-R. JIANG Too Many Redundant Calls! ¨ How to remove redundancy? ¤ Prevent repeated calculation Recursion True dependency Dynamic programming 22 5 4 3 2 1 5 4 3 2 3 2 1 2 1 0 1 0 1 1 0 3 2 3 1 2 1 0 1 1 0 2 1 0 2 1 0 2 1 0 IRIS H.-R. JIANG Dynamic Programming -- Memoization ¨ Store the values in a table ¤ Check the table before a recursive call ¤ Top-down! n The control flow is almost the same as the original one Dynamic programming 23 fib(n) 1. Initialize f[0..n] with -1 // -1: unfilled 2. f[0] = 0; f[1] = 1 3. fibonacci(n, f) fibonacci(n, f) 1. If f[n] == -1 then 2. f[n] = fibonacci(n ! 1, f) + fibonacci(n ! 2, f) 3. return f[n] // if f[n] already exists, directly return 5 4 3 2 1 IRIS H.-R. JIANG Dynamic Programming -- Bottom-up? ¨ Store the values in a table ¤ Bottom-up n Compute the values for small problems first ¤ Much like induction Dynamic programming 24 fib(n) 1. initialize f[1..n] with -1 // -1: unfilled 2. f[0] = 0; f[1] = 1 3. for i=2 to n do 4. f[i] = f[i-1]+ f[i-2] 5. return f[n] 5 4 3 2 1
- 23. IRIS H.-R. JIANG What’s Wrong? ¨ What if we call fib(5)? ¤ fib(5) ¤ fib(4) + fib(3) ¤ (fib(3) + fib(2)) + (fib(2) + fib(1)) ¤ ((fib(2) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1)) ¤ (((fib(1) + fib(0)) + fib(1))+(fib(1) + fib(0)))+((fib(1) + fib(0))+fib(1)) ¤ A call tree that calls the function on the same value many different times n fib(2) was calculated three times from scratch n Impractical for large n Dynamic programming 21 fib(n) 1. if n £ 1 return n 2. return fib(n ! 1) + fib(n ! 2) 5 4 3 2 3 2 1 2 1 0 1 0 1 1 0 2 1 0 2 1 0 2 1 0 IRIS H.-R. JIANG Too Many Redundant Calls! ¨ How to remove redundancy? ¤ Prevent repeated calculation Recursion True dependency Dynamic programming 22 5 4 3 2 1 5 4 3 2 3 2 1 2 1 0 1 0 1 1 0 3 2 3 1 2 1 0 1 1 0 2 1 0 2 1 0 2 1 0 IRIS H.-R. JIANG Dynamic Programming -- Memoization ¨ Store the values in a table ¤ Check the table before a recursive call ¤ Top-down! n The control flow is almost the same as the original one Dynamic programming 23 fib(n) 1. Initialize f[0..n] with -1 // -1: unfilled 2. f[0] = 0; f[1] = 1 3. fibonacci(n, f) fibonacci(n, f) 1. If f[n] == -1 then 2. f[n] = fibonacci(n ! 1, f) + fibonacci(n ! 2, f) 3. return f[n] // if f[n] already exists, directly return 5 4 3 2 1 IRIS H.-R. JIANG Dynamic Programming -- Bottom-up? ¨ Store the values in a table ¤ Bottom-up n Compute the values for small problems first ¤ Much like induction Dynamic programming 24 fib(n) 1. initialize f[1..n] with -1 // -1: unfilled 2. f[0] = 0; f[1] = 1 3. for i=2 to n do 4. f[i] = f[i-1]+ f[i-2] 5. return f[n] 5 4 3 2 1
- 24. IRIS H.-R. JIANG What’s Wrong? ¨ What if we call fib(5)? ¤ fib(5) ¤ fib(4) + fib(3) ¤ (fib(3) + fib(2)) + (fib(2) + fib(1)) ¤ ((fib(2) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1)) ¤ (((fib(1) + fib(0)) + fib(1))+(fib(1) + fib(0)))+((fib(1) + fib(0))+fib(1)) ¤ A call tree that calls the function on the same value many different times n fib(2) was calculated three times from scratch n Impractical for large n Dynamic programming 21 fib(n) 1. if n £ 1 return n 2. return fib(n ! 1) + fib(n ! 2) 5 4 3 2 3 2 1 2 1 0 1 0 1 1 0 2 1 0 2 1 0 2 1 0 IRIS H.-R. JIANG Too Many Redundant Calls! ¨ How to remove redundancy? ¤ Prevent repeated calculation Recursion True dependency Dynamic programming 22 5 4 3 2 1 5 4 3 2 3 2 1 2 1 0 1 0 1 1 0 3 2 3 1 2 1 0 1 1 0 2 1 0 2 1 0 2 1 0 IRIS H.-R. JIANG Dynamic Programming -- Memoization ¨ Store the values in a table ¤ Check the table before a recursive call ¤ Top-down! n The control flow is almost the same as the original one Dynamic programming 23 fib(n) 1. Initialize f[0..n] with -1 // -1: unfilled 2. f[0] = 0; f[1] = 1 3. fibonacci(n, f) fibonacci(n, f) 1. If f[n] == -1 then 2. f[n] = fibonacci(n ! 1, f) + fibonacci(n ! 2, f) 3. return f[n] // if f[n] already exists, directly return 5 4 3 2 1 IRIS H.-R. JIANG Dynamic Programming -- Bottom-up? ¨ Store the values in a table ¤ Bottom-up n Compute the values for small problems first ¤ Much like induction Dynamic programming 24 fib(n) 1. initialize f[1..n] with -1 // -1: unfilled 2. f[0] = 0; f[1] = 1 3. for i=2 to n do 4. f[i] = f[i-1]+ f[i-2] 5. return f[n] 5 4 3 2 1
- 25. Appendix: Maze Routing 25 Dynamic programming 1 1 1 1 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5 5 5 5 6 6 6 6 6 6 6 6 6 6 6 6 2 2 2 2 2 2 2 8 8 8 8 8 8 8 8 8 7 7 7 7 7 7 7 7 7 9 9 9 9 9 9 9 9 9 9 10 10 10 10 10 10 10 10 10 11 11 11 11 11 11 11 11 11 12 12 12 12 12 12 12 12 12 12 12 IRIS H.-R. JIANG Maze Routing Problem ¨ Restrictions: Two-pin nets on single-layer rectilinear routing ¨ Given: ¤ A planar rectangular grid graph ¤ Two points S and T on the graph ¤ Obstacles modeled as blocked vertices ¨ Find: ¤ The shortest path connecting S and T ¨ Applications: Routing in IC design Dynamic programming 26 S T IRIS H.-R. JIANG Lee’s Algorithm (1/2) ¨ Idea: ¤ Bottom up dynamic programming: Induction on path length ¨ Procedure: 1. Wave propagation 2. Retrace Dynamic programming 27 T S 1 1 1 1 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5 5 5 5 6 6 6 6 6 6 6 6 6 6 6 6 2 2 2 2 2 2 2 8 8 8 8 8 8 8 8 8 7 7 7 7 7 7 7 7 7 9 9 9 9 9 9 9 9 9 9 10 10 10 10 10 10 10 10 10 11 11 11 11 11 11 11 11 11 12 12 12 12 12 12 12 12 12 12 12 C. Y. Lee, “An algorithm for path connection and its application,” IRE Trans. Electronic Computer, vol. EC-10, no. 2, pp. 364-365, 1961. IRIS H.-R. JIANG Lee’s Algorithm (2/2) ¨ Strengths ¤ Guarantee to find connection between 2 terminals if it exists ¤ Guarantee minimum path ¨ Weaknesses ¤ Large memory for dense layout ¤ Slow ¨ Running time ¤ O(MN) for M´N grid Dynamic programming 28 T S 1 1 1 1 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5 5 5 5 6 6 6 6 6 6 6 6 6 6 6 6 2 2 2 2 2 2 2 8 8 8 8 8 8 8 8 8 7 7 7 7 7 7 7 7 7 9 9 9 9 9 9 9 9 9 9 10 10 10 10 10 10 10 10 10 11 11 11 11 11 11 11 11 11 12 12 12 12 12 12 12 12 12 12 12
- 26. Appendix: Maze Routing 25 Dynamic programming 1 1 1 1 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5 5 5 5 6 6 6 6 6 6 6 6 6 6 6 6 2 2 2 2 2 2 2 8 8 8 8 8 8 8 8 8 7 7 7 7 7 7 7 7 7 9 9 9 9 9 9 9 9 9 9 10 10 10 10 10 10 10 10 10 11 11 11 11 11 11 11 11 11 12 12 12 12 12 12 12 12 12 12 12 IRIS H.-R. JIANG Maze Routing Problem ¨ Restrictions: Two-pin nets on single-layer rectilinear routing ¨ Given: ¤ A planar rectangular grid graph ¤ Two points S and T on the graph ¤ Obstacles modeled as blocked vertices ¨ Find: ¤ The shortest path connecting S and T ¨ Applications: Routing in IC design Dynamic programming 26 S T IRIS H.-R. JIANG Lee’s Algorithm (1/2) ¨ Idea: ¤ Bottom up dynamic programming: Induction on path length ¨ Procedure: 1. Wave propagation 2. Retrace Dynamic programming 27 T S 1 1 1 1 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5 5 5 5 6 6 6 6 6 6 6 6 6 6 6 6 2 2 2 2 2 2 2 8 8 8 8 8 8 8 8 8 7 7 7 7 7 7 7 7 7 9 9 9 9 9 9 9 9 9 9 10 10 10 10 10 10 10 10 10 11 11 11 11 11 11 11 11 11 12 12 12 12 12 12 12 12 12 12 12 C. Y. Lee, “An algorithm for path connection and its application,” IRE Trans. Electronic Computer, vol. EC-10, no. 2, pp. 364-365, 1961. IRIS H.-R. JIANG Lee’s Algorithm (2/2) ¨ Strengths ¤ Guarantee to find connection between 2 terminals if it exists ¤ Guarantee minimum path ¨ Weaknesses ¤ Large memory for dense layout ¤ Slow ¨ Running time ¤ O(MN) for M´N grid Dynamic programming 28 T S 1 1 1 1 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5 5 5 5 6 6 6 6 6 6 6 6 6 6 6 6 2 2 2 2 2 2 2 8 8 8 8 8 8 8 8 8 7 7 7 7 7 7 7 7 7 9 9 9 9 9 9 9 9 9 9 10 10 10 10 10 10 10 10 10 11 11 11 11 11 11 11 11 11 12 12 12 12 12 12 12 12 12 12 12
- 27. Appendix: Maze Routing 25 Dynamic programming 1 1 1 1 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5 5 5 5 6 6 6 6 6 6 6 6 6 6 6 6 2 2 2 2 2 2 2 8 8 8 8 8 8 8 8 8 7 7 7 7 7 7 7 7 7 9 9 9 9 9 9 9 9 9 9 10 10 10 10 10 10 10 10 10 11 11 11 11 11 11 11 11 11 12 12 12 12 12 12 12 12 12 12 12 IRIS H.-R. JIANG Maze Routing Problem ¨ Restrictions: Two-pin nets on single-layer rectilinear routing ¨ Given: ¤ A planar rectangular grid graph ¤ Two points S and T on the graph ¤ Obstacles modeled as blocked vertices ¨ Find: ¤ The shortest path connecting S and T ¨ Applications: Routing in IC design Dynamic programming 26 S T IRIS H.-R. JIANG Lee’s Algorithm (1/2) ¨ Idea: ¤ Bottom up dynamic programming: Induction on path length ¨ Procedure: 1. Wave propagation 2. Retrace Dynamic programming 27 T S 1 1 1 1 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5 5 5 5 6 6 6 6 6 6 6 6 6 6 6 6 2 2 2 2 2 2 2 8 8 8 8 8 8 8 8 8 7 7 7 7 7 7 7 7 7 9 9 9 9 9 9 9 9 9 9 10 10 10 10 10 10 10 10 10 11 11 11 11 11 11 11 11 11 12 12 12 12 12 12 12 12 12 12 12 C. Y. Lee, “An algorithm for path connection and its application,” IRE Trans. Electronic Computer, vol. EC-10, no. 2, pp. 364-365, 1961. IRIS H.-R. JIANG Lee’s Algorithm (2/2) ¨ Strengths ¤ Guarantee to find connection between 2 terminals if it exists ¤ Guarantee minimum path ¨ Weaknesses ¤ Large memory for dense layout ¤ Slow ¨ Running time ¤ O(MN) for M´N grid Dynamic programming 28 T S 1 1 1 1 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5 5 5 5 6 6 6 6 6 6 6 6 6 6 6 6 2 2 2 2 2 2 2 8 8 8 8 8 8 8 8 8 7 7 7 7 7 7 7 7 7 9 9 9 9 9 9 9 9 9 9 10 10 10 10 10 10 10 10 10 11 11 11 11 11 11 11 11 11 12 12 12 12 12 12 12 12 12 12 12
- 28. Appendix: Maze Routing 25 Dynamic programming 1 1 1 1 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5 5 5 5 6 6 6 6 6 6 6 6 6 6 6 6 2 2 2 2 2 2 2 8 8 8 8 8 8 8 8 8 7 7 7 7 7 7 7 7 7 9 9 9 9 9 9 9 9 9 9 10 10 10 10 10 10 10 10 10 11 11 11 11 11 11 11 11 11 12 12 12 12 12 12 12 12 12 12 12 IRIS H.-R. JIANG Maze Routing Problem ¨ Restrictions: Two-pin nets on single-layer rectilinear routing ¨ Given: ¤ A planar rectangular grid graph ¤ Two points S and T on the graph ¤ Obstacles modeled as blocked vertices ¨ Find: ¤ The shortest path connecting S and T ¨ Applications: Routing in IC design Dynamic programming 26 S T IRIS H.-R. JIANG Lee’s Algorithm (1/2) ¨ Idea: ¤ Bottom up dynamic programming: Induction on path length ¨ Procedure: 1. Wave propagation 2. Retrace Dynamic programming 27 T S 1 1 1 1 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5 5 5 5 6 6 6 6 6 6 6 6 6 6 6 6 2 2 2 2 2 2 2 8 8 8 8 8 8 8 8 8 7 7 7 7 7 7 7 7 7 9 9 9 9 9 9 9 9 9 9 10 10 10 10 10 10 10 10 10 11 11 11 11 11 11 11 11 11 12 12 12 12 12 12 12 12 12 12 12 C. Y. Lee, “An algorithm for path connection and its application,” IRE Trans. Electronic Computer, vol. EC-10, no. 2, pp. 364-365, 1961. IRIS H.-R. JIANG Lee’s Algorithm (2/2) ¨ Strengths ¤ Guarantee to find connection between 2 terminals if it exists ¤ Guarantee minimum path ¨ Weaknesses ¤ Large memory for dense layout ¤ Slow ¨ Running time ¤ O(MN) for M´N grid Dynamic programming 28 T S 1 1 1 1 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5 5 5 5 6 6 6 6 6 6 6 6 6 6 6 6 2 2 2 2 2 2 2 8 8 8 8 8 8 8 8 8 7 7 7 7 7 7 7 7 7 9 9 9 9 9 9 9 9 9 9 10 10 10 10 10 10 10 10 10 11 11 11 11 11 11 11 11 11 12 12 12 12 12 12 12 12 12 12 12
- 29. Adding a variable Subset Sums & Knapsacks 29 Dynamic programming IRIS H.-R. JIANG Subset Sum ¨ Given ¤ A set of n items and a knapsack n Item i weighs wi > 0. n The knapsack has capacity of W. ¨ Goal: ¤ Fill the knapsack so as to maximize total weight. n maximize SiÎS wi ¨ Greedy ¹ optimal ¤ Largest wi first: 7+2+1 = 10 ¤ Optimal: 5+6 = 11 Dynamic programming 30 Karp's 21 NP-complete problems: R. M. Karp, "Reducibility among combinatorial problems". Complexity of Computer Computations. pp. 85–103. 1 Weight 5 6 2 7 Item 1 3 4 5 2 W = 11 1 Weight 5 6 2 7 Item 1 3 4 5 2 W = 11 1 Weight 5 6 2 7 Item 1 3 4 5 2 W = 11 IRIS H.-R. JIANG Dynamic Programming: False Start ¨ Optimization problem formulation ¤ max SiÎS wi s.t. SiÎS wi < W, SÍ{1, …, n} ¨ OPT(i) = the total weight of the optimal solution for items 1, …, i ¤ OPT(i) = maxS SjÎS wj, SÍ{1, …, i} ¨ Consider OPT(n), i.e., the total weight of the final solution O ¤ Case 1: nÏO (OPT(n) does not count wn) n OPT(n) = OPT(n-1) (Optimal solution of {1, 2, …, n-1}) ¤ Case 2: nÎO (OPT(n) counts wn) n OPT(n) = wn + OPT(n-1) Dynamic programming 31 Q: What’s wrong? A: Accept item n Þ For items {1, 2, …, n-1}, we have less available weight, W - wn objective function constraints IRIS H.-R. JIANG ¨ Optimization problem formulation ¤ max SiÎS wi s.t. SiÎS wi < W, SÍ{1, …, n} ¨ OPT(i) depends not only on items {1, …, i} but also on W ¤ OPT(i, w) = maxS SjÎS wj, SÍ{1, …, i} and SjÎS wj < w ¨ Consider OPT(n), i.e., the total weight of the final solution O ¤ Case 1: nÏO (OPT(n) does not count wn) n OPT(n, w) = OPT(n-1, w) ¤ Case 2: nÎO (OPT(n) counts wn) n OPT(n, w) = wn + OPT(n-1, w-wn ) ¨ Recurrence relation: ¤ Adding a New Variable Dynamic programming 32 ¤ OPT(i) = maxS SjÎS wj, SÍ{1, …, i} n OPT(n) = OPT(n-1) (Optimal solution of {1, 2, …, n-1}) n OPT(n) = wn + OPT(n-1) OPT(i, w) = 0 if i or w=0 OPT(i-1, w) if wi > w max {OPT(i-1, w), wi + OPT(i-1, w-wi)} otherwise
- 30. Adding a variable Subset Sums & Knapsacks 29 Dynamic programming IRIS H.-R. JIANG Subset Sum ¨ Given ¤ A set of n items and a knapsack n Item i weighs wi > 0. n The knapsack has capacity of W. ¨ Goal: ¤ Fill the knapsack so as to maximize total weight. n maximize SiÎS wi ¨ Greedy ¹ optimal ¤ Largest wi first: 7+2+1 = 10 ¤ Optimal: 5+6 = 11 Dynamic programming 30 Karp's 21 NP-complete problems: R. M. Karp, "Reducibility among combinatorial problems". Complexity of Computer Computations. pp. 85–103. 1 Weight 5 6 2 7 Item 1 3 4 5 2 W = 11 1 Weight 5 6 2 7 Item 1 3 4 5 2 W = 11 1 Weight 5 6 2 7 Item 1 3 4 5 2 W = 11 IRIS H.-R. JIANG Dynamic Programming: False Start ¨ Optimization problem formulation ¤ max SiÎS wi s.t. SiÎS wi < W, SÍ{1, …, n} ¨ OPT(i) = the total weight of the optimal solution for items 1, …, i ¤ OPT(i) = maxS SjÎS wj, SÍ{1, …, i} ¨ Consider OPT(n), i.e., the total weight of the final solution O ¤ Case 1: nÏO (OPT(n) does not count wn) n OPT(n) = OPT(n-1) (Optimal solution of {1, 2, …, n-1}) ¤ Case 2: nÎO (OPT(n) counts wn) n OPT(n) = wn + OPT(n-1) Dynamic programming 31 Q: What’s wrong? A: Accept item n Þ For items {1, 2, …, n-1}, we have less available weight, W - wn objective function constraints IRIS H.-R. JIANG ¨ Optimization problem formulation ¤ max SiÎS wi s.t. SiÎS wi < W, SÍ{1, …, n} ¨ OPT(i) depends not only on items {1, …, i} but also on W ¤ OPT(i, w) = maxS SjÎS wj, SÍ{1, …, i} and SjÎS wj < w ¨ Consider OPT(n), i.e., the total weight of the final solution O ¤ Case 1: nÏO (OPT(n) does not count wn) n OPT(n, w) = OPT(n-1, w) ¤ Case 2: nÎO (OPT(n) counts wn) n OPT(n, w) = wn + OPT(n-1, w-wn ) ¨ Recurrence relation: ¤ Adding a New Variable Dynamic programming 32 ¤ OPT(i) = maxS SjÎS wj, SÍ{1, …, i} n OPT(n) = OPT(n-1) (Optimal solution of {1, 2, …, n-1}) n OPT(n) = wn + OPT(n-1) OPT(i, w) = 0 if i or w=0 OPT(i-1, w) if wi > w max {OPT(i-1, w), wi + OPT(i-1, w-wi)} otherwise
- 31. Adding a variable Subset Sums & Knapsacks 29 Dynamic programming IRIS H.-R. JIANG Subset Sum ¨ Given ¤ A set of n items and a knapsack n Item i weighs wi > 0. n The knapsack has capacity of W. ¨ Goal: ¤ Fill the knapsack so as to maximize total weight. n maximize SiÎS wi ¨ Greedy ¹ optimal ¤ Largest wi first: 7+2+1 = 10 ¤ Optimal: 5+6 = 11 Dynamic programming 30 Karp's 21 NP-complete problems: R. M. Karp, "Reducibility among combinatorial problems". Complexity of Computer Computations. pp. 85–103. 1 Weight 5 6 2 7 Item 1 3 4 5 2 W = 11 1 Weight 5 6 2 7 Item 1 3 4 5 2 W = 11 1 Weight 5 6 2 7 Item 1 3 4 5 2 W = 11 IRIS H.-R. JIANG Dynamic Programming: False Start ¨ Optimization problem formulation ¤ max SiÎS wi s.t. SiÎS wi < W, SÍ{1, …, n} ¨ OPT(i) = the total weight of the optimal solution for items 1, …, i ¤ OPT(i) = maxS SjÎS wj, SÍ{1, …, i} ¨ Consider OPT(n), i.e., the total weight of the final solution O ¤ Case 1: nÏO (OPT(n) does not count wn) n OPT(n) = OPT(n-1) (Optimal solution of {1, 2, …, n-1}) ¤ Case 2: nÎO (OPT(n) counts wn) n OPT(n) = wn + OPT(n-1) Dynamic programming 31 Q: What’s wrong? A: Accept item n Þ For items {1, 2, …, n-1}, we have less available weight, W - wn objective function constraints IRIS H.-R. JIANG ¨ Optimization problem formulation ¤ max SiÎS wi s.t. SiÎS wi < W, SÍ{1, …, n} ¨ OPT(i) depends not only on items {1, …, i} but also on W ¤ OPT(i, w) = maxS SjÎS wj, SÍ{1, …, i} and SjÎS wj < w ¨ Consider OPT(n), i.e., the total weight of the final solution O ¤ Case 1: nÏO (OPT(n) does not count wn) n OPT(n, w) = OPT(n-1, w) ¤ Case 2: nÎO (OPT(n) counts wn) n OPT(n, w) = wn + OPT(n-1, w-wn ) ¨ Recurrence relation: ¤ Adding a New Variable Dynamic programming 32 ¤ OPT(i) = maxS SjÎS wj, SÍ{1, …, i} n OPT(n) = OPT(n-1) (Optimal solution of {1, 2, …, n-1}) n OPT(n) = wn + OPT(n-1) OPT(i, w) = 0 if i or w=0 OPT(i-1, w) if wi > w max {OPT(i-1, w), wi + OPT(i-1, w-wi)} otherwise
- 32. Adding a variable Subset Sums & Knapsacks 29 Dynamic programming IRIS H.-R. JIANG Subset Sum ¨ Given ¤ A set of n items and a knapsack n Item i weighs wi > 0. n The knapsack has capacity of W. ¨ Goal: ¤ Fill the knapsack so as to maximize total weight. n maximize SiÎS wi ¨ Greedy ¹ optimal ¤ Largest wi first: 7+2+1 = 10 ¤ Optimal: 5+6 = 11 Dynamic programming 30 Karp's 21 NP-complete problems: R. M. Karp, "Reducibility among combinatorial problems". Complexity of Computer Computations. pp. 85–103. 1 Weight 5 6 2 7 Item 1 3 4 5 2 W = 11 1 Weight 5 6 2 7 Item 1 3 4 5 2 W = 11 1 Weight 5 6 2 7 Item 1 3 4 5 2 W = 11 IRIS H.-R. JIANG Dynamic Programming: False Start ¨ Optimization problem formulation ¤ max SiÎS wi s.t. SiÎS wi < W, SÍ{1, …, n} ¨ OPT(i) = the total weight of the optimal solution for items 1, …, i ¤ OPT(i) = maxS SjÎS wj, SÍ{1, …, i} ¨ Consider OPT(n), i.e., the total weight of the final solution O ¤ Case 1: nÏO (OPT(n) does not count wn) n OPT(n) = OPT(n-1) (Optimal solution of {1, 2, …, n-1}) ¤ Case 2: nÎO (OPT(n) counts wn) n OPT(n) = wn + OPT(n-1) Dynamic programming 31 Q: What’s wrong? A: Accept item n Þ For items {1, 2, …, n-1}, we have less available weight, W - wn objective function constraints IRIS H.-R. JIANG ¨ Optimization problem formulation ¤ max SiÎS wi s.t. SiÎS wi < W, SÍ{1, …, n} ¨ OPT(i) depends not only on items {1, …, i} but also on W ¤ OPT(i, w) = maxS SjÎS wj, SÍ{1, …, i} and SjÎS wj < w ¨ Consider OPT(n), i.e., the total weight of the final solution O ¤ Case 1: nÏO (OPT(n) does not count wn) n OPT(n, w) = OPT(n-1, w) ¤ Case 2: nÎO (OPT(n) counts wn) n OPT(n, w) = wn + OPT(n-1, w-wn ) ¨ Recurrence relation: ¤ Adding a New Variable Dynamic programming 32 ¤ OPT(i) = maxS SjÎS wj, SÍ{1, …, i} n OPT(n) = OPT(n-1) (Optimal solution of {1, 2, …, n-1}) n OPT(n) = wn + OPT(n-1) OPT(i, w) = 0 if i or w=0 OPT(i-1, w) if wi > w max {OPT(i-1, w), wi + OPT(i-1, w-wi)} otherwise
- 33. IRIS H.-R. JIANG DP: Iteration Dynamic programming 33 OPT(i, w) = 0 if i, w = 0 OPT(i-1, w) if wi > w max {OPT(i-1, w), wi + OPT(i-1, w-wi)} otherwise Subset-sum(n, w1,…, wn, W) 1. for w = 0, 1, …, W do 2. M[0, w] = 0 3. for i = 0, 1, …, n do 4. M[i, 0] = 0 5. for i = 1, 2, .., n do 6. for w = 1, 2, .., W do 7. if (wi > w) then 8. M[i, w] = M[i-1, w] 9. else 10. M[i, w] = max {M[i-1, w], wi +M[i-1, w-wi]} IRIS H.-R. JIANG Example Dynamic programming 34 1 Weight 5 6 2 7 Item 1 3 4 5 2 W = 11 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 3 3 3 3 3 3 3 3 3 1 2 3 3 5 6 7 8 8 8 8 1 2 3 3 5 6 7 8 9 9 11 1 1 1 1 1 1 1 1 1 1 1 1 2 3 3 5 6 7 8 9 10 11 0 1 2 3 4 5 6 7 8 9 10 11 W + 1 Æ { 1, 2 } { 1, 2, 3 } { 1, 2, 3, 4 } { 1 } { 1, 2, 3, 4, 5 } n + 1 Subset-sum(n, w1,…, wn, W) 1. for w = 0, 1, …, W do 2. M[0, w] = 0 3. for i = 0, 1, …, n do 4. M[i, 0] = 0 5. for i = 1, 2, .., n do 6. for w = 1, 2, .., W do 7. if (wi > w) then 8. M[i, w] = M[i-1, w] 9. else 10. M[i, w] = max{M[i-1, w], wi +M[i-1, w-wi]} 3 11 11 M 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 3 3 3 3 3 3 3 3 3 1 2 3 3 5 6 7 8 8 8 8 1 2 3 3 5 6 7 8 9 9 11 1 1 1 1 1 1 1 1 1 1 1 1 2 3 3 5 6 7 8 9 10 11 Running time: O(nW) IRIS H.-R. JIANG Pseudo-Polynomial Running Time ¨ Running time: O(nW) ¤ W is not polynomial in input size ¤ “Pseudo-polynomial” ¤ In fact, the subset sum is a computationally hard problem! n r.f. Karp's 21 NP-complete problems: n R. M. Karp, "Reducibility among combinatorial problems". Complexity of Computer Computations. pp. 85--103. Dynamic programming 35 IRIS H.-R. JIANG The Knapsack Problem ¨ Given ¤ A set of n items and a knapsack ¤ Item i weighs wi > 0 and has value vi > 0. ¤ The knapsack has capacity of W. ¨ Goal: ¤ Fill the knapsack so as to maximize total value. n Maximize SiÎS vi ¨ Optimization problem formulation ¤ max SiÎS vi s.t. SiÎS wi < W, SÍ{1, …, n} ¨ Greedy ¹ optimal ¤ Largest vi first: 28+6+1 = 35 ¤ Optimal: 18+22 = 40 Dynamic programming 36 ue. Karp's 21 NP-complete problems: R. M. Karp, "Reducibility among combinatorial problems". Complexity of Computer Computations. pp. 85–103. 1 Value 18 22 28 1 Weight 5 6 6 2 7 Item 1 3 4 5 2 W = 11
- 34. IRIS H.-R. JIANG DP: Iteration Dynamic programming 33 OPT(i, w) = 0 if i, w = 0 OPT(i-1, w) if wi > w max {OPT(i-1, w), wi + OPT(i-1, w-wi)} otherwise Subset-sum(n, w1,…, wn, W) 1. for w = 0, 1, …, W do 2. M[0, w] = 0 3. for i = 0, 1, …, n do 4. M[i, 0] = 0 5. for i = 1, 2, .., n do 6. for w = 1, 2, .., W do 7. if (wi > w) then 8. M[i, w] = M[i-1, w] 9. else 10. M[i, w] = max {M[i-1, w], wi +M[i-1, w-wi]} IRIS H.-R. JIANG Example Dynamic programming 34 1 Weight 5 6 2 7 Item 1 3 4 5 2 W = 11 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 3 3 3 3 3 3 3 3 3 1 2 3 3 5 6 7 8 8 8 8 1 2 3 3 5 6 7 8 9 9 11 1 1 1 1 1 1 1 1 1 1 1 1 2 3 3 5 6 7 8 9 10 11 0 1 2 3 4 5 6 7 8 9 10 11 W + 1 Æ { 1, 2 } { 1, 2, 3 } { 1, 2, 3, 4 } { 1 } { 1, 2, 3, 4, 5 } n + 1 Subset-sum(n, w1,…, wn, W) 1. for w = 0, 1, …, W do 2. M[0, w] = 0 3. for i = 0, 1, …, n do 4. M[i, 0] = 0 5. for i = 1, 2, .., n do 6. for w = 1, 2, .., W do 7. if (wi > w) then 8. M[i, w] = M[i-1, w] 9. else 10. M[i, w] = max{M[i-1, w], wi +M[i-1, w-wi]} 3 11 11 M 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 3 3 3 3 3 3 3 3 3 1 2 3 3 5 6 7 8 8 8 8 1 2 3 3 5 6 7 8 9 9 11 1 1 1 1 1 1 1 1 1 1 1 1 2 3 3 5 6 7 8 9 10 11 Running time: O(nW) IRIS H.-R. JIANG Pseudo-Polynomial Running Time ¨ Running time: O(nW) ¤ W is not polynomial in input size ¤ “Pseudo-polynomial” ¤ In fact, the subset sum is a computationally hard problem! n r.f. Karp's 21 NP-complete problems: n R. M. Karp, "Reducibility among combinatorial problems". Complexity of Computer Computations. pp. 85--103. Dynamic programming 35 IRIS H.-R. JIANG The Knapsack Problem ¨ Given ¤ A set of n items and a knapsack ¤ Item i weighs wi > 0 and has value vi > 0. ¤ The knapsack has capacity of W. ¨ Goal: ¤ Fill the knapsack so as to maximize total value. n Maximize SiÎS vi ¨ Optimization problem formulation ¤ max SiÎS vi s.t. SiÎS wi < W, SÍ{1, …, n} ¨ Greedy ¹ optimal ¤ Largest vi first: 28+6+1 = 35 ¤ Optimal: 18+22 = 40 Dynamic programming 36 ue. Karp's 21 NP-complete problems: R. M. Karp, "Reducibility among combinatorial problems". Complexity of Computer Computations. pp. 85–103. 1 Value 18 22 28 1 Weight 5 6 6 2 7 Item 1 3 4 5 2 W = 11
- 35. IRIS H.-R. JIANG DP: Iteration Dynamic programming 33 OPT(i, w) = 0 if i, w = 0 OPT(i-1, w) if wi > w max {OPT(i-1, w), wi + OPT(i-1, w-wi)} otherwise Subset-sum(n, w1,…, wn, W) 1. for w = 0, 1, …, W do 2. M[0, w] = 0 3. for i = 0, 1, …, n do 4. M[i, 0] = 0 5. for i = 1, 2, .., n do 6. for w = 1, 2, .., W do 7. if (wi > w) then 8. M[i, w] = M[i-1, w] 9. else 10. M[i, w] = max {M[i-1, w], wi +M[i-1, w-wi]} IRIS H.-R. JIANG Example Dynamic programming 34 1 Weight 5 6 2 7 Item 1 3 4 5 2 W = 11 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 3 3 3 3 3 3 3 3 3 1 2 3 3 5 6 7 8 8 8 8 1 2 3 3 5 6 7 8 9 9 11 1 1 1 1 1 1 1 1 1 1 1 1 2 3 3 5 6 7 8 9 10 11 0 1 2 3 4 5 6 7 8 9 10 11 W + 1 Æ { 1, 2 } { 1, 2, 3 } { 1, 2, 3, 4 } { 1 } { 1, 2, 3, 4, 5 } n + 1 Subset-sum(n, w1,…, wn, W) 1. for w = 0, 1, …, W do 2. M[0, w] = 0 3. for i = 0, 1, …, n do 4. M[i, 0] = 0 5. for i = 1, 2, .., n do 6. for w = 1, 2, .., W do 7. if (wi > w) then 8. M[i, w] = M[i-1, w] 9. else 10. M[i, w] = max{M[i-1, w], wi +M[i-1, w-wi]} 3 11 11 M 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 3 3 3 3 3 3 3 3 3 1 2 3 3 5 6 7 8 8 8 8 1 2 3 3 5 6 7 8 9 9 11 1 1 1 1 1 1 1 1 1 1 1 1 2 3 3 5 6 7 8 9 10 11 Running time: O(nW) IRIS H.-R. JIANG Pseudo-Polynomial Running Time ¨ Running time: O(nW) ¤ W is not polynomial in input size ¤ “Pseudo-polynomial” ¤ In fact, the subset sum is a computationally hard problem! n r.f. Karp's 21 NP-complete problems: n R. M. Karp, "Reducibility among combinatorial problems". Complexity of Computer Computations. pp. 85--103. Dynamic programming 35 IRIS H.-R. JIANG The Knapsack Problem ¨ Given ¤ A set of n items and a knapsack ¤ Item i weighs wi > 0 and has value vi > 0. ¤ The knapsack has capacity of W. ¨ Goal: ¤ Fill the knapsack so as to maximize total value. n Maximize SiÎS vi ¨ Optimization problem formulation ¤ max SiÎS vi s.t. SiÎS wi < W, SÍ{1, …, n} ¨ Greedy ¹ optimal ¤ Largest vi first: 28+6+1 = 35 ¤ Optimal: 18+22 = 40 Dynamic programming 36 ue. Karp's 21 NP-complete problems: R. M. Karp, "Reducibility among combinatorial problems". Complexity of Computer Computations. pp. 85–103. 1 Value 18 22 28 1 Weight 5 6 6 2 7 Item 1 3 4 5 2 W = 11
- 36. IRIS H.-R. JIANG DP: Iteration Dynamic programming 33 OPT(i, w) = 0 if i, w = 0 OPT(i-1, w) if wi > w max {OPT(i-1, w), wi + OPT(i-1, w-wi)} otherwise Subset-sum(n, w1,…, wn, W) 1. for w = 0, 1, …, W do 2. M[0, w] = 0 3. for i = 0, 1, …, n do 4. M[i, 0] = 0 5. for i = 1, 2, .., n do 6. for w = 1, 2, .., W do 7. if (wi > w) then 8. M[i, w] = M[i-1, w] 9. else 10. M[i, w] = max {M[i-1, w], wi +M[i-1, w-wi]} IRIS H.-R. JIANG Example Dynamic programming 34 1 Weight 5 6 2 7 Item 1 3 4 5 2 W = 11 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 3 3 3 3 3 3 3 3 3 1 2 3 3 5 6 7 8 8 8 8 1 2 3 3 5 6 7 8 9 9 11 1 1 1 1 1 1 1 1 1 1 1 1 2 3 3 5 6 7 8 9 10 11 0 1 2 3 4 5 6 7 8 9 10 11 W + 1 Æ { 1, 2 } { 1, 2, 3 } { 1, 2, 3, 4 } { 1 } { 1, 2, 3, 4, 5 } n + 1 Subset-sum(n, w1,…, wn, W) 1. for w = 0, 1, …, W do 2. M[0, w] = 0 3. for i = 0, 1, …, n do 4. M[i, 0] = 0 5. for i = 1, 2, .., n do 6. for w = 1, 2, .., W do 7. if (wi > w) then 8. M[i, w] = M[i-1, w] 9. else 10. M[i, w] = max{M[i-1, w], wi +M[i-1, w-wi]} 3 11 11 M 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 3 3 3 3 3 3 3 3 3 1 2 3 3 5 6 7 8 8 8 8 1 2 3 3 5 6 7 8 9 9 11 1 1 1 1 1 1 1 1 1 1 1 1 2 3 3 5 6 7 8 9 10 11 Running time: O(nW) IRIS H.-R. JIANG Pseudo-Polynomial Running Time ¨ Running time: O(nW) ¤ W is not polynomial in input size ¤ “Pseudo-polynomial” ¤ In fact, the subset sum is a computationally hard problem! n r.f. Karp's 21 NP-complete problems: n R. M. Karp, "Reducibility among combinatorial problems". Complexity of Computer Computations. pp. 85--103. Dynamic programming 35 IRIS H.-R. JIANG The Knapsack Problem ¨ Given ¤ A set of n items and a knapsack ¤ Item i weighs wi > 0 and has value vi > 0. ¤ The knapsack has capacity of W. ¨ Goal: ¤ Fill the knapsack so as to maximize total value. n Maximize SiÎS vi ¨ Optimization problem formulation ¤ max SiÎS vi s.t. SiÎS wi < W, SÍ{1, …, n} ¨ Greedy ¹ optimal ¤ Largest vi first: 28+6+1 = 35 ¤ Optimal: 18+22 = 40 Dynamic programming 36 ue. Karp's 21 NP-complete problems: R. M. Karp, "Reducibility among combinatorial problems". Complexity of Computer Computations. pp. 85–103. 1 Value 18 22 28 1 Weight 5 6 6 2 7 Item 1 3 4 5 2 W = 11
- 37. IRIS H.-R. JIANG Recurrence Relation ¨ We know the recurrence relation for the subset sum problem: ¨ Q: How about the Knapsack problem? ¨ A: Dynamic programming 37 OPT(i, w) = 0 if i, w = 0 OPT(i-1, w) if wi > w max {OPT(i-1, w), wi + OPT(i-1, w-wi)} otherwise OPT(i, w) = 0 if i, w = 0 OPT(i-1, w) if wi > w max {OPT(i-1, w), vi + OPT(i-1, w-wi)} otherwise Richard E. Bellman Lester R. Ford, Jr. Shortest Path – Bellman-Ford 38 Dynamic programming R. E. Bellman 1920—1984 Invention of DP, 1953 IRIS H.-R. JIANG Recap: Dijkstra’s Algorithm ¨ The shortest path problem: ¨ Given: ¤ Directed graph G = (V, E), source s and destination t n cost cuv = length of edge (u, v) Î E ¨ Goal: ¤ Find the shortest path from s to t n Length of path P: c(P)= S(u, v)ÎP cuv ¨ Q: What if negative edge costs? Dynamic programming 39 Dijkstra(G,c) // S: the set of explored nodes // d(u): shortest path distance from s to u 1. initialize S = {s}, d(s) = 0 2. while S ¹ V do 3. select node v Ï S with at least one edge from S 4. d'(v) = min(u, v): uÎS d(u)+cuv 5. add v to S and define d(v) = d'(v) ce ³ 0 s a b t 2 1 3 -6 s 0 1 2 1 t 2 a 5 b 5 Q: What’s wrong with s-a-b-t path? IRIS H.-R. JIANG Modifying Dijkstra’s Algorithm? ¨ Observation: A path that starts on a cheap edge may cost more than a path that starts on an expensive edge, but then compensates with subsequent edges of negative cost. ¨ Reweighting: Increase the costs of all the edges by the same amount so that all costs become nonnegative. ¨ Q: What’s wrong?! ¨ A: Adapting the costs changes the minimum-cost path. ¤ c’(s-a-b-t) = c(s-a-b-t) + 3*6; c’(s-t) = c(s-t) + 6 ¤ Different paths change by different amounts. Dynamic programming 40 s a b t 2 1 3 -6 s a b t 8 7 9 0 +6 Dijkstra s a b t 8 7 9 0 s 0 7 t 1 t s 2 a b 5 t -1
- 38. IRIS H.-R. JIANG Recurrence Relation ¨ We know the recurrence relation for the subset sum problem: ¨ Q: How about the Knapsack problem? ¨ A: Dynamic programming 37 OPT(i, w) = 0 if i, w = 0 OPT(i-1, w) if wi > w max {OPT(i-1, w), wi + OPT(i-1, w-wi)} otherwise OPT(i, w) = 0 if i, w = 0 OPT(i-1, w) if wi > w max {OPT(i-1, w), vi + OPT(i-1, w-wi)} otherwise Richard E. Bellman Lester R. Ford, Jr. Shortest Path – Bellman-Ford 38 Dynamic programming R. E. Bellman 1920—1984 Invention of DP, 1953 IRIS H.-R. JIANG Recap: Dijkstra’s Algorithm ¨ The shortest path problem: ¨ Given: ¤ Directed graph G = (V, E), source s and destination t n cost cuv = length of edge (u, v) Î E ¨ Goal: ¤ Find the shortest path from s to t n Length of path P: c(P)= S(u, v)ÎP cuv ¨ Q: What if negative edge costs? Dynamic programming 39 Dijkstra(G,c) // S: the set of explored nodes // d(u): shortest path distance from s to u 1. initialize S = {s}, d(s) = 0 2. while S ¹ V do 3. select node v Ï S with at least one edge from S 4. d'(v) = min(u, v): uÎS d(u)+cuv 5. add v to S and define d(v) = d'(v) ce ³ 0 s a b t 2 1 3 -6 s 0 1 2 1 t 2 a 5 b 5 Q: What’s wrong with s-a-b-t path? IRIS H.-R. JIANG Modifying Dijkstra’s Algorithm? ¨ Observation: A path that starts on a cheap edge may cost more than a path that starts on an expensive edge, but then compensates with subsequent edges of negative cost. ¨ Reweighting: Increase the costs of all the edges by the same amount so that all costs become nonnegative. ¨ Q: What’s wrong?! ¨ A: Adapting the costs changes the minimum-cost path. ¤ c’(s-a-b-t) = c(s-a-b-t) + 3*6; c’(s-t) = c(s-t) + 6 ¤ Different paths change by different amounts. Dynamic programming 40 s a b t 2 1 3 -6 s a b t 8 7 9 0 +6 Dijkstra s a b t 8 7 9 0 s 0 7 t 1 t s 2 a b 5 t -1
- 39. IRIS H.-R. JIANG Recurrence Relation ¨ We know the recurrence relation for the subset sum problem: ¨ Q: How about the Knapsack problem? ¨ A: Dynamic programming 37 OPT(i, w) = 0 if i, w = 0 OPT(i-1, w) if wi > w max {OPT(i-1, w), wi + OPT(i-1, w-wi)} otherwise OPT(i, w) = 0 if i, w = 0 OPT(i-1, w) if wi > w max {OPT(i-1, w), vi + OPT(i-1, w-wi)} otherwise Richard E. Bellman Lester R. Ford, Jr. Shortest Path – Bellman-Ford 38 Dynamic programming R. E. Bellman 1920—1984 Invention of DP, 1953 IRIS H.-R. JIANG Recap: Dijkstra’s Algorithm ¨ The shortest path problem: ¨ Given: ¤ Directed graph G = (V, E), source s and destination t n cost cuv = length of edge (u, v) Î E ¨ Goal: ¤ Find the shortest path from s to t n Length of path P: c(P)= S(u, v)ÎP cuv ¨ Q: What if negative edge costs? Dynamic programming 39 Dijkstra(G,c) // S: the set of explored nodes // d(u): shortest path distance from s to u 1. initialize S = {s}, d(s) = 0 2. while S ¹ V do 3. select node v Ï S with at least one edge from S 4. d'(v) = min(u, v): uÎS d(u)+cuv 5. add v to S and define d(v) = d'(v) ce ³ 0 s a b t 2 1 3 -6 s 0 1 2 1 t 2 a 5 b 5 Q: What’s wrong with s-a-b-t path? IRIS H.-R. JIANG Modifying Dijkstra’s Algorithm? ¨ Observation: A path that starts on a cheap edge may cost more than a path that starts on an expensive edge, but then compensates with subsequent edges of negative cost. ¨ Reweighting: Increase the costs of all the edges by the same amount so that all costs become nonnegative. ¨ Q: What’s wrong?! ¨ A: Adapting the costs changes the minimum-cost path. ¤ c’(s-a-b-t) = c(s-a-b-t) + 3*6; c’(s-t) = c(s-t) + 6 ¤ Different paths change by different amounts. Dynamic programming 40 s a b t 2 1 3 -6 s a b t 8 7 9 0 +6 Dijkstra s a b t 8 7 9 0 s 0 7 t 1 t s 2 a b 5 t -1
- 40. IRIS H.-R. JIANG Recurrence Relation ¨ We know the recurrence relation for the subset sum problem: ¨ Q: How about the Knapsack problem? ¨ A: Dynamic programming 37 OPT(i, w) = 0 if i, w = 0 OPT(i-1, w) if wi > w max {OPT(i-1, w), wi + OPT(i-1, w-wi)} otherwise OPT(i, w) = 0 if i, w = 0 OPT(i-1, w) if wi > w max {OPT(i-1, w), vi + OPT(i-1, w-wi)} otherwise Richard E. Bellman Lester R. Ford, Jr. Shortest Path – Bellman-Ford 38 Dynamic programming R. E. Bellman 1920—1984 Invention of DP, 1953 IRIS H.-R. JIANG Recap: Dijkstra’s Algorithm ¨ The shortest path problem: ¨ Given: ¤ Directed graph G = (V, E), source s and destination t n cost cuv = length of edge (u, v) Î E ¨ Goal: ¤ Find the shortest path from s to t n Length of path P: c(P)= S(u, v)ÎP cuv ¨ Q: What if negative edge costs? Dynamic programming 39 Dijkstra(G,c) // S: the set of explored nodes // d(u): shortest path distance from s to u 1. initialize S = {s}, d(s) = 0 2. while S ¹ V do 3. select node v Ï S with at least one edge from S 4. d'(v) = min(u, v): uÎS d(u)+cuv 5. add v to S and define d(v) = d'(v) ce ³ 0 s a b t 2 1 3 -6 s 0 1 2 1 t 2 a 5 b 5 Q: What’s wrong with s-a-b-t path? IRIS H.-R. JIANG Modifying Dijkstra’s Algorithm? ¨ Observation: A path that starts on a cheap edge may cost more than a path that starts on an expensive edge, but then compensates with subsequent edges of negative cost. ¨ Reweighting: Increase the costs of all the edges by the same amount so that all costs become nonnegative. ¨ Q: What’s wrong?! ¨ A: Adapting the costs changes the minimum-cost path. ¤ c’(s-a-b-t) = c(s-a-b-t) + 3*6; c’(s-t) = c(s-t) + 6 ¤ Different paths change by different amounts. Dynamic programming 40 s a b t 2 1 3 -6 s a b t 8 7 9 0 +6 Dijkstra s a b t 8 7 9 0 s 0 7 t 1 t s 2 a b 5 t -1
- 41. IRIS H.-R. JIANG Bellman-Ford Algorithm (1/2) ¨ Induction either on nodes or on edges works! ¨ If G has no negative cycles, then there is a shortest path from s to t that is simple (i.e., does not repeat nodes), and hence has at most n-1 edges. ¨ Pf: ¤ Suppose the shortest path P from s to t repeat a node v. ¤ Since every cycle has nonnegative cost, we could remove the portion of P between consecutive visits to v resulting in a simple path Q of no greater cost and fewer edges. n c(Q) = c(P) – c(C) £ c(P) Dynamic programming 41 v s t C c(C) ³ 0 IRIS H.-R. JIANG Bellman-Ford Algorithm (2/2) ¨ Induction on edges ¨ OPT(i, v) = length of shortest v-t path P using at most i edges. ¤ OPT(n-1, s) = length of shortest s-t path. ¤ Case 1: P uses at most i-1 edges. n OPT(i, v) = OPT(i-1, v) ¤ Case 2: P uses exactly i edges. n OPT(i, v) = cvw + OPT(i-1, w) n If (v, w) is the first edge, then P uses (v, w) and then selects the shortest w-t path using at most i-1 edges Dynamic programming 42 v t at most i-1 edges : : w OPT(i, v) = 0 if i = 0, v = t ¥ if i = 0, v ¹ t min{OPT(i-1, v), min(v, w)ÎE {cvw + OPT(i-1, w)}} otherwise t at most i-1 edges v IRIS H.-R. JIANG Implementation: Iteration Dynamic programming 43 Bellman-Ford(G, s, t) // n = # of nodes in G // M[0.. n-1, V]: table recording optimal solutions of subproblems 1. M[0, t] = 0 2. foreach vÎV-{t} do 3. M[0, v] = ¥ 4. for i = 1 to n-1 do 5. for vÎV in any order do 6. M[i, v]=min{M[i-1, v], min(v, w)ÎE {cvw + M[i-1, w]}} OPT(i, v) = 0 if i = 0, v = t ¥ if i = 0, v ¹ t min{OPT(i-1, v), min(v, w)ÎE {cvw + OPT(i-1, w)}} otherwise IRIS H.-R. JIANG M Example Dynamic programming 44 Bellman-Ford(G, s, t) // n = # of nodes in G // M[0.. n-1, V]: table recording optimal solutions of subproblems 1. M[0, t] = 0 2. foreach vÎV-{t} do 3. M[0, v] = ¥ 4. for i = 1 to n-1 do 5. for vÎV in any order do 6. M[i, v]=min{M[i-1, v], min(v, w)ÎE {cvw + M[i-1, w]}} ¥ ¥ ¥ ¥ ¥ 0 ¥ 3 4 -3 2 0 0 3 3 -3 0 0 -2 3 3 -4 0 0 -2 3 2 -6 0 0 -2 3 0 -6 0 0 1 2 3 4 5 n t b c d a e n 0 Space: O(n2) Running time: 1. naïve: O(n3) 2. detailed: O(nm) b d t e -1 -2 4 2 c -3 8 a -4 6 -3 3 ¥ ¥ ¥ ¥ ¥ 0 ¥ 3 4 -3 2 0 0 3 3 -3 0 0 -2 3 3 -4 0 0 -2 3 2 -6 0 0 -2 3 0 -6 0 0 b t e c a Q: How to find the shortest path? A: Record “successor” for each entry M[d, 2] =min{M[d,1], cda+M[a,1]}
- 42. IRIS H.-R. JIANG Bellman-Ford Algorithm (1/2) ¨ Induction either on nodes or on edges works! ¨ If G has no negative cycles, then there is a shortest path from s to t that is simple (i.e., does not repeat nodes), and hence has at most n-1 edges. ¨ Pf: ¤ Suppose the shortest path P from s to t repeat a node v. ¤ Since every cycle has nonnegative cost, we could remove the portion of P between consecutive visits to v resulting in a simple path Q of no greater cost and fewer edges. n c(Q) = c(P) – c(C) £ c(P) Dynamic programming 41 v s t C c(C) ³ 0 IRIS H.-R. JIANG Bellman-Ford Algorithm (2/2) ¨ Induction on edges ¨ OPT(i, v) = length of shortest v-t path P using at most i edges. ¤ OPT(n-1, s) = length of shortest s-t path. ¤ Case 1: P uses at most i-1 edges. n OPT(i, v) = OPT(i-1, v) ¤ Case 2: P uses exactly i edges. n OPT(i, v) = cvw + OPT(i-1, w) n If (v, w) is the first edge, then P uses (v, w) and then selects the shortest w-t path using at most i-1 edges Dynamic programming 42 v t at most i-1 edges : : w OPT(i, v) = 0 if i = 0, v = t ¥ if i = 0, v ¹ t min{OPT(i-1, v), min(v, w)ÎE {cvw + OPT(i-1, w)}} otherwise t at most i-1 edges v IRIS H.-R. JIANG Implementation: Iteration Dynamic programming 43 Bellman-Ford(G, s, t) // n = # of nodes in G // M[0.. n-1, V]: table recording optimal solutions of subproblems 1. M[0, t] = 0 2. foreach vÎV-{t} do 3. M[0, v] = ¥ 4. for i = 1 to n-1 do 5. for vÎV in any order do 6. M[i, v]=min{M[i-1, v], min(v, w)ÎE {cvw + M[i-1, w]}} OPT(i, v) = 0 if i = 0, v = t ¥ if i = 0, v ¹ t min{OPT(i-1, v), min(v, w)ÎE {cvw + OPT(i-1, w)}} otherwise IRIS H.-R. JIANG M Example Dynamic programming 44 Bellman-Ford(G, s, t) // n = # of nodes in G // M[0.. n-1, V]: table recording optimal solutions of subproblems 1. M[0, t] = 0 2. foreach vÎV-{t} do 3. M[0, v] = ¥ 4. for i = 1 to n-1 do 5. for vÎV in any order do 6. M[i, v]=min{M[i-1, v], min(v, w)ÎE {cvw + M[i-1, w]}} ¥ ¥ ¥ ¥ ¥ 0 ¥ 3 4 -3 2 0 0 3 3 -3 0 0 -2 3 3 -4 0 0 -2 3 2 -6 0 0 -2 3 0 -6 0 0 1 2 3 4 5 n t b c d a e n 0 Space: O(n2) Running time: 1. naïve: O(n3) 2. detailed: O(nm) b d t e -1 -2 4 2 c -3 8 a -4 6 -3 3 ¥ ¥ ¥ ¥ ¥ 0 ¥ 3 4 -3 2 0 0 3 3 -3 0 0 -2 3 3 -4 0 0 -2 3 2 -6 0 0 -2 3 0 -6 0 0 b t e c a Q: How to find the shortest path? A: Record “successor” for each entry M[d, 2] =min{M[d,1], cda+M[a,1]}
- 43. IRIS H.-R. JIANG Bellman-Ford Algorithm (1/2) ¨ Induction either on nodes or on edges works! ¨ If G has no negative cycles, then there is a shortest path from s to t that is simple (i.e., does not repeat nodes), and hence has at most n-1 edges. ¨ Pf: ¤ Suppose the shortest path P from s to t repeat a node v. ¤ Since every cycle has nonnegative cost, we could remove the portion of P between consecutive visits to v resulting in a simple path Q of no greater cost and fewer edges. n c(Q) = c(P) – c(C) £ c(P) Dynamic programming 41 v s t C c(C) ³ 0 IRIS H.-R. JIANG Bellman-Ford Algorithm (2/2) ¨ Induction on edges ¨ OPT(i, v) = length of shortest v-t path P using at most i edges. ¤ OPT(n-1, s) = length of shortest s-t path. ¤ Case 1: P uses at most i-1 edges. n OPT(i, v) = OPT(i-1, v) ¤ Case 2: P uses exactly i edges. n OPT(i, v) = cvw + OPT(i-1, w) n If (v, w) is the first edge, then P uses (v, w) and then selects the shortest w-t path using at most i-1 edges Dynamic programming 42 v t at most i-1 edges : : w OPT(i, v) = 0 if i = 0, v = t ¥ if i = 0, v ¹ t min{OPT(i-1, v), min(v, w)ÎE {cvw + OPT(i-1, w)}} otherwise t at most i-1 edges v IRIS H.-R. JIANG Implementation: Iteration Dynamic programming 43 Bellman-Ford(G, s, t) // n = # of nodes in G // M[0.. n-1, V]: table recording optimal solutions of subproblems 1. M[0, t] = 0 2. foreach vÎV-{t} do 3. M[0, v] = ¥ 4. for i = 1 to n-1 do 5. for vÎV in any order do 6. M[i, v]=min{M[i-1, v], min(v, w)ÎE {cvw + M[i-1, w]}} OPT(i, v) = 0 if i = 0, v = t ¥ if i = 0, v ¹ t min{OPT(i-1, v), min(v, w)ÎE {cvw + OPT(i-1, w)}} otherwise IRIS H.-R. JIANG M Example Dynamic programming 44 Bellman-Ford(G, s, t) // n = # of nodes in G // M[0.. n-1, V]: table recording optimal solutions of subproblems 1. M[0, t] = 0 2. foreach vÎV-{t} do 3. M[0, v] = ¥ 4. for i = 1 to n-1 do 5. for vÎV in any order do 6. M[i, v]=min{M[i-1, v], min(v, w)ÎE {cvw + M[i-1, w]}} ¥ ¥ ¥ ¥ ¥ 0 ¥ 3 4 -3 2 0 0 3 3 -3 0 0 -2 3 3 -4 0 0 -2 3 2 -6 0 0 -2 3 0 -6 0 0 1 2 3 4 5 n t b c d a e n 0 Space: O(n2) Running time: 1. naïve: O(n3) 2. detailed: O(nm) b d t e -1 -2 4 2 c -3 8 a -4 6 -3 3 ¥ ¥ ¥ ¥ ¥ 0 ¥ 3 4 -3 2 0 0 3 3 -3 0 0 -2 3 3 -4 0 0 -2 3 2 -6 0 0 -2 3 0 -6 0 0 b t e c a Q: How to find the shortest path? A: Record “successor” for each entry M[d, 2] =min{M[d,1], cda+M[a,1]}
- 44. IRIS H.-R. JIANG Bellman-Ford Algorithm (1/2) ¨ Induction either on nodes or on edges works! ¨ If G has no negative cycles, then there is a shortest path from s to t that is simple (i.e., does not repeat nodes), and hence has at most n-1 edges. ¨ Pf: ¤ Suppose the shortest path P from s to t repeat a node v. ¤ Since every cycle has nonnegative cost, we could remove the portion of P between consecutive visits to v resulting in a simple path Q of no greater cost and fewer edges. n c(Q) = c(P) – c(C) £ c(P) Dynamic programming 41 v s t C c(C) ³ 0 IRIS H.-R. JIANG Bellman-Ford Algorithm (2/2) ¨ Induction on edges ¨ OPT(i, v) = length of shortest v-t path P using at most i edges. ¤ OPT(n-1, s) = length of shortest s-t path. ¤ Case 1: P uses at most i-1 edges. n OPT(i, v) = OPT(i-1, v) ¤ Case 2: P uses exactly i edges. n OPT(i, v) = cvw + OPT(i-1, w) n If (v, w) is the first edge, then P uses (v, w) and then selects the shortest w-t path using at most i-1 edges Dynamic programming 42 v t at most i-1 edges : : w OPT(i, v) = 0 if i = 0, v = t ¥ if i = 0, v ¹ t min{OPT(i-1, v), min(v, w)ÎE {cvw + OPT(i-1, w)}} otherwise t at most i-1 edges v IRIS H.-R. JIANG Implementation: Iteration Dynamic programming 43 Bellman-Ford(G, s, t) // n = # of nodes in G // M[0.. n-1, V]: table recording optimal solutions of subproblems 1. M[0, t] = 0 2. foreach vÎV-{t} do 3. M[0, v] = ¥ 4. for i = 1 to n-1 do 5. for vÎV in any order do 6. M[i, v]=min{M[i-1, v], min(v, w)ÎE {cvw + M[i-1, w]}} OPT(i, v) = 0 if i = 0, v = t ¥ if i = 0, v ¹ t min{OPT(i-1, v), min(v, w)ÎE {cvw + OPT(i-1, w)}} otherwise IRIS H.-R. JIANG M Example Dynamic programming 44 Bellman-Ford(G, s, t) // n = # of nodes in G // M[0.. n-1, V]: table recording optimal solutions of subproblems 1. M[0, t] = 0 2. foreach vÎV-{t} do 3. M[0, v] = ¥ 4. for i = 1 to n-1 do 5. for vÎV in any order do 6. M[i, v]=min{M[i-1, v], min(v, w)ÎE {cvw + M[i-1, w]}} ¥ ¥ ¥ ¥ ¥ 0 ¥ 3 4 -3 2 0 0 3 3 -3 0 0 -2 3 3 -4 0 0 -2 3 2 -6 0 0 -2 3 0 -6 0 0 1 2 3 4 5 n t b c d a e n 0 Space: O(n2) Running time: 1. naïve: O(n3) 2. detailed: O(nm) b d t e -1 -2 4 2 c -3 8 a -4 6 -3 3 ¥ ¥ ¥ ¥ ¥ 0 ¥ 3 4 -3 2 0 0 3 3 -3 0 0 -2 3 3 -4 0 0 -2 3 2 -6 0 0 -2 3 0 -6 0 0 b t e c a Q: How to find the shortest path? A: Record “successor” for each entry M[d, 2] =min{M[d,1], cda+M[a,1]}
- 45. IRIS H.-R. JIANG Running Time ¨ Lines 5-6: ¤ Naïve: for each v, check v and others: O(n2) ¤ Detailed: for each v, check v and its neighbors (out-going edges): åvÎV(degout(v)+1) = O(m) ¨ Lines 4-6: ¤ Naïve: O(n3) ¤ Detailed: O(nm) Dynamic programming 45 0 1 2 3 4 5 n t b c d a e n ¥ ¥ ¥ ¥ ¥ 0 ¥ 3 4 -3 2 0 0 3 3 -3 0 0 -2 3 3 -4 0 0 -2 3 2 -6 0 0 -2 3 0 -6 0 0 b d t e -1 -2 4 2 c -3 8 a -4 6 -3 3 Bellman-Ford(G, s, t) : 4. for i = 1 to n-1 do 5. for vÎV in any order do 6. M[i, v]=min{M[i-1, v], min(v, w)ÎE {cvw + M[i-1, w]}} IRIS H.-R. JIANG Space Improvement ¨ Maintain a 1D array instead: ¤ M[v] = shortest v-t path length that we have found so far. ¤ Iterator i is simply a counter ¤ No need to check edges of the form (v, w) unless M[w] changed in previous iteration. ¤ In each iteration, for each node v, M[v]=min{M[v], minwÎV {cvw + M[w]}} ¨ Observation: Throughout the algorithm, M[v] is the length of some v-t path, and after i rounds of updates, the value M[v] is no larger than the length of shortest v-t path using at most i edges. Dynamic programming 46 Computing Science is –and will always be– concerned with the interplay between mechanized and human symbol manipulation, which usually referred to as “computing” and “programming” respectively. ~ E. W. Dijkstra IRIS H.-R. JIANG Negative Cycles? ¨ If a s-t path in a general graph G passes through node v, and v belongs to a negative cycle C, Bellman-Ford algorithm fails to find the shortest s-t path. ¤ Reduce cost over and over again using the negative cycle Dynamic programming 47 v s t C c(C) < 0 IRIS H.-R. JIANG Application: Currency Conversion (1/2) ¨ Q: Given n currencies and exchange rates between pairs of currencies, is there an arbitrage opportunity? ¤ The currency graph: n Node: currency; edge cost: exchange rate ruv: ruv*rvu <1 ¤ Arbitrage: a cycle on which product of edge costs >1 n E.g., $1 Þ 1.3941 Francs Þ 0.9308 Euros Þ $1.00084 Dynamic programming 48 Courtesy of Prof. Kevin Wayne @ Princeton G £ F E ¥ $ 0.003065 455.2 208.1 0.004816 2.1904 1.3941 0.6677 327.25 129.52 0.008309 1.0752 $ 1.3941 F 0.6677 E 1.0752
- 46. IRIS H.-R. JIANG Running Time ¨ Lines 5-6: ¤ Naïve: for each v, check v and others: O(n2) ¤ Detailed: for each v, check v and its neighbors (out-going edges): åvÎV(degout(v)+1) = O(m) ¨ Lines 4-6: ¤ Naïve: O(n3) ¤ Detailed: O(nm) Dynamic programming 45 0 1 2 3 4 5 n t b c d a e n ¥ ¥ ¥ ¥ ¥ 0 ¥ 3 4 -3 2 0 0 3 3 -3 0 0 -2 3 3 -4 0 0 -2 3 2 -6 0 0 -2 3 0 -6 0 0 b d t e -1 -2 4 2 c -3 8 a -4 6 -3 3 Bellman-Ford(G, s, t) : 4. for i = 1 to n-1 do 5. for vÎV in any order do 6. M[i, v]=min{M[i-1, v], min(v, w)ÎE {cvw + M[i-1, w]}} IRIS H.-R. JIANG Space Improvement ¨ Maintain a 1D array instead: ¤ M[v] = shortest v-t path length that we have found so far. ¤ Iterator i is simply a counter ¤ No need to check edges of the form (v, w) unless M[w] changed in previous iteration. ¤ In each iteration, for each node v, M[v]=min{M[v], minwÎV {cvw + M[w]}} ¨ Observation: Throughout the algorithm, M[v] is the length of some v-t path, and after i rounds of updates, the value M[v] is no larger than the length of shortest v-t path using at most i edges. Dynamic programming 46 Computing Science is –and will always be– concerned with the interplay between mechanized and human symbol manipulation, which usually referred to as “computing” and “programming” respectively. ~ E. W. Dijkstra IRIS H.-R. JIANG Negative Cycles? ¨ If a s-t path in a general graph G passes through node v, and v belongs to a negative cycle C, Bellman-Ford algorithm fails to find the shortest s-t path. ¤ Reduce cost over and over again using the negative cycle Dynamic programming 47 v s t C c(C) < 0 IRIS H.-R. JIANG Application: Currency Conversion (1/2) ¨ Q: Given n currencies and exchange rates between pairs of currencies, is there an arbitrage opportunity? ¤ The currency graph: n Node: currency; edge cost: exchange rate ruv: ruv*rvu <1 ¤ Arbitrage: a cycle on which product of edge costs >1 n E.g., $1 Þ 1.3941 Francs Þ 0.9308 Euros Þ $1.00084 Dynamic programming 48 Courtesy of Prof. Kevin Wayne @ Princeton G £ F E ¥ $ 0.003065 455.2 208.1 0.004816 2.1904 1.3941 0.6677 327.25 129.52 0.008309 1.0752 $ 1.3941 F 0.6677 E 1.0752
- 47. IRIS H.-R. JIANG Running Time ¨ Lines 5-6: ¤ Naïve: for each v, check v and others: O(n2) ¤ Detailed: for each v, check v and its neighbors (out-going edges): åvÎV(degout(v)+1) = O(m) ¨ Lines 4-6: ¤ Naïve: O(n3) ¤ Detailed: O(nm) Dynamic programming 45 0 1 2 3 4 5 n t b c d a e n ¥ ¥ ¥ ¥ ¥ 0 ¥ 3 4 -3 2 0 0 3 3 -3 0 0 -2 3 3 -4 0 0 -2 3 2 -6 0 0 -2 3 0 -6 0 0 b d t e -1 -2 4 2 c -3 8 a -4 6 -3 3 Bellman-Ford(G, s, t) : 4. for i = 1 to n-1 do 5. for vÎV in any order do 6. M[i, v]=min{M[i-1, v], min(v, w)ÎE {cvw + M[i-1, w]}} IRIS H.-R. JIANG Space Improvement ¨ Maintain a 1D array instead: ¤ M[v] = shortest v-t path length that we have found so far. ¤ Iterator i is simply a counter ¤ No need to check edges of the form (v, w) unless M[w] changed in previous iteration. ¤ In each iteration, for each node v, M[v]=min{M[v], minwÎV {cvw + M[w]}} ¨ Observation: Throughout the algorithm, M[v] is the length of some v-t path, and after i rounds of updates, the value M[v] is no larger than the length of shortest v-t path using at most i edges. Dynamic programming 46 Computing Science is –and will always be– concerned with the interplay between mechanized and human symbol manipulation, which usually referred to as “computing” and “programming” respectively. ~ E. W. Dijkstra IRIS H.-R. JIANG Negative Cycles? ¨ If a s-t path in a general graph G passes through node v, and v belongs to a negative cycle C, Bellman-Ford algorithm fails to find the shortest s-t path. ¤ Reduce cost over and over again using the negative cycle Dynamic programming 47 v s t C c(C) < 0 IRIS H.-R. JIANG Application: Currency Conversion (1/2) ¨ Q: Given n currencies and exchange rates between pairs of currencies, is there an arbitrage opportunity? ¤ The currency graph: n Node: currency; edge cost: exchange rate ruv: ruv*rvu <1 ¤ Arbitrage: a cycle on which product of edge costs >1 n E.g., $1 Þ 1.3941 Francs Þ 0.9308 Euros Þ $1.00084 Dynamic programming 48 Courtesy of Prof. Kevin Wayne @ Princeton G £ F E ¥ $ 0.003065 455.2 208.1 0.004816 2.1904 1.3941 0.6677 327.25 129.52 0.008309 1.0752 $ 1.3941 F 0.6677 E 1.0752
- 48. IRIS H.-R. JIANG Running Time ¨ Lines 5-6: ¤ Naïve: for each v, check v and others: O(n2) ¤ Detailed: for each v, check v and its neighbors (out-going edges): åvÎV(degout(v)+1) = O(m) ¨ Lines 4-6: ¤ Naïve: O(n3) ¤ Detailed: O(nm) Dynamic programming 45 0 1 2 3 4 5 n t b c d a e n ¥ ¥ ¥ ¥ ¥ 0 ¥ 3 4 -3 2 0 0 3 3 -3 0 0 -2 3 3 -4 0 0 -2 3 2 -6 0 0 -2 3 0 -6 0 0 b d t e -1 -2 4 2 c -3 8 a -4 6 -3 3 Bellman-Ford(G, s, t) : 4. for i = 1 to n-1 do 5. for vÎV in any order do 6. M[i, v]=min{M[i-1, v], min(v, w)ÎE {cvw + M[i-1, w]}} IRIS H.-R. JIANG Space Improvement ¨ Maintain a 1D array instead: ¤ M[v] = shortest v-t path length that we have found so far. ¤ Iterator i is simply a counter ¤ No need to check edges of the form (v, w) unless M[w] changed in previous iteration. ¤ In each iteration, for each node v, M[v]=min{M[v], minwÎV {cvw + M[w]}} ¨ Observation: Throughout the algorithm, M[v] is the length of some v-t path, and after i rounds of updates, the value M[v] is no larger than the length of shortest v-t path using at most i edges. Dynamic programming 46 Computing Science is –and will always be– concerned with the interplay between mechanized and human symbol manipulation, which usually referred to as “computing” and “programming” respectively. ~ E. W. Dijkstra IRIS H.-R. JIANG Negative Cycles? ¨ If a s-t path in a general graph G passes through node v, and v belongs to a negative cycle C, Bellman-Ford algorithm fails to find the shortest s-t path. ¤ Reduce cost over and over again using the negative cycle Dynamic programming 47 v s t C c(C) < 0 IRIS H.-R. JIANG Application: Currency Conversion (1/2) ¨ Q: Given n currencies and exchange rates between pairs of currencies, is there an arbitrage opportunity? ¤ The currency graph: n Node: currency; edge cost: exchange rate ruv: ruv*rvu <1 ¤ Arbitrage: a cycle on which product of edge costs >1 n E.g., $1 Þ 1.3941 Francs Þ 0.9308 Euros Þ $1.00084 Dynamic programming 48 Courtesy of Prof. Kevin Wayne @ Princeton G £ F E ¥ $ 0.003065 455.2 208.1 0.004816 2.1904 1.3941 0.6677 327.25 129.52 0.008309 1.0752 $ 1.3941 F 0.6677 E 1.0752
- 49. IRIS H.-R. JIANG Application: Currency Conversion (2/2) ¨ Product of edge costs on a cycle C = v1, v2, …, v1 ¤ rv1v2*rv2v3*…*rvnv1 ¤ Arbitrage: rv1v2*rv2v3*…*rvnv1>1 ¨ Sum of edge costs on a cycle C = v1, v2, …, v1 ¤ cv1v2+cv2v3+…+cvnv1 ¤ cuv = - lg ruv Arbitrage Negative cycle 49 Dynamic programming G £ F E ¥ $ 0.003065 455.2 208.1 0.004816 2.1904 1.3941 0.6677 327.25 129.52 0.008309 1.0752 $ 1.3941 F 0.6677 E 1.0752 -0.4793 0.5827 -0.1046 -0.4793+0.5827-0.1046 < 0 Arbitrage = negative cycle IRIS H.-R. JIANG Negative Cycle Detection ¨ If OPT(n, v) = OPT(n-1, v) for all v, then no negative cycles. ¤ Bellman-Ford: OPT(i, v) = OPT(n-1, v) for all v and i ³ n. ¨ If OPT(n, v) < OPT(n-1, v) for some v, then shortest path contains a negative cycle ¨ Pf: by contradiction ¤ Since OPT(n, v) < OPT(n-1, v), P has exactly n edges. ¤ Every path using at most n-1 edges costs more than P. ¤ (By pigeonhole principle,) P must contain a cycle C. ¤ If C were not a negative cycle, deleting C yields a v-t path with < n edges and no greater cost. ®¬ Dynamic programming 50 w v t C c(C) ³ 0 w v t C c(C) < 0 IRIS H.-R. JIANG Detecting Negative Cycles by Bellman-Ford ¨ Augmented graph G’ of G 1. Add new node t 2. Connect all nodes to t with 0-cost edge ¨ G has a negative cycle iff G’ has a negative cycle reaching t ¨ Check if OPT(n, v) = OPT(n-1, v): ¤ If yes, no negative cycles ¤ If no, then extract cycle from shortest path from v to t ¨ Procedure: ¤ Build the augmented graph G’ for G ¤ Run Bellman-Ford on G’ for n iterations (instead of n-1). ¤ Upon termination, Bellman-Ford successor variables trace a negative cycle if one exists. Dynamic programming 51 t 0 0 0 0 0 Q: Why? Richard E. Bellman, 1962 Traveling Salesman Problem 52 Dynamic programming R. Bellman, Dynamic programming treatment of the travelling salesman problem. J. ACM 9, 1, Jan. 1962, pp. 61-63.
- 50. IRIS H.-R. JIANG Application: Currency Conversion (2/2) ¨ Product of edge costs on a cycle C = v1, v2, …, v1 ¤ rv1v2*rv2v3*…*rvnv1 ¤ Arbitrage: rv1v2*rv2v3*…*rvnv1>1 ¨ Sum of edge costs on a cycle C = v1, v2, …, v1 ¤ cv1v2+cv2v3+…+cvnv1 ¤ cuv = - lg ruv Arbitrage Negative cycle 49 Dynamic programming G £ F E ¥ $ 0.003065 455.2 208.1 0.004816 2.1904 1.3941 0.6677 327.25 129.52 0.008309 1.0752 $ 1.3941 F 0.6677 E 1.0752 -0.4793 0.5827 -0.1046 -0.4793+0.5827-0.1046 < 0 Arbitrage = negative cycle IRIS H.-R. JIANG Negative Cycle Detection ¨ If OPT(n, v) = OPT(n-1, v) for all v, then no negative cycles. ¤ Bellman-Ford: OPT(i, v) = OPT(n-1, v) for all v and i ³ n. ¨ If OPT(n, v) < OPT(n-1, v) for some v, then shortest path contains a negative cycle ¨ Pf: by contradiction ¤ Since OPT(n, v) < OPT(n-1, v), P has exactly n edges. ¤ Every path using at most n-1 edges costs more than P. ¤ (By pigeonhole principle,) P must contain a cycle C. ¤ If C were not a negative cycle, deleting C yields a v-t path with < n edges and no greater cost. ®¬ Dynamic programming 50 w v t C c(C) ³ 0 w v t C c(C) < 0 IRIS H.-R. JIANG Detecting Negative Cycles by Bellman-Ford ¨ Augmented graph G’ of G 1. Add new node t 2. Connect all nodes to t with 0-cost edge ¨ G has a negative cycle iff G’ has a negative cycle reaching t ¨ Check if OPT(n, v) = OPT(n-1, v): ¤ If yes, no negative cycles ¤ If no, then extract cycle from shortest path from v to t ¨ Procedure: ¤ Build the augmented graph G’ for G ¤ Run Bellman-Ford on G’ for n iterations (instead of n-1). ¤ Upon termination, Bellman-Ford successor variables trace a negative cycle if one exists. Dynamic programming 51 t 0 0 0 0 0 Q: Why? Richard E. Bellman, 1962 Traveling Salesman Problem 52 Dynamic programming R. Bellman, Dynamic programming treatment of the travelling salesman problem. J. ACM 9, 1, Jan. 1962, pp. 61-63.
- 51. IRIS H.-R. JIANG Application: Currency Conversion (2/2) ¨ Product of edge costs on a cycle C = v1, v2, …, v1 ¤ rv1v2*rv2v3*…*rvnv1 ¤ Arbitrage: rv1v2*rv2v3*…*rvnv1>1 ¨ Sum of edge costs on a cycle C = v1, v2, …, v1 ¤ cv1v2+cv2v3+…+cvnv1 ¤ cuv = - lg ruv Arbitrage Negative cycle 49 Dynamic programming G £ F E ¥ $ 0.003065 455.2 208.1 0.004816 2.1904 1.3941 0.6677 327.25 129.52 0.008309 1.0752 $ 1.3941 F 0.6677 E 1.0752 -0.4793 0.5827 -0.1046 -0.4793+0.5827-0.1046 < 0 Arbitrage = negative cycle IRIS H.-R. JIANG Negative Cycle Detection ¨ If OPT(n, v) = OPT(n-1, v) for all v, then no negative cycles. ¤ Bellman-Ford: OPT(i, v) = OPT(n-1, v) for all v and i ³ n. ¨ If OPT(n, v) < OPT(n-1, v) for some v, then shortest path contains a negative cycle ¨ Pf: by contradiction ¤ Since OPT(n, v) < OPT(n-1, v), P has exactly n edges. ¤ Every path using at most n-1 edges costs more than P. ¤ (By pigeonhole principle,) P must contain a cycle C. ¤ If C were not a negative cycle, deleting C yields a v-t path with < n edges and no greater cost. ®¬ Dynamic programming 50 w v t C c(C) ³ 0 w v t C c(C) < 0 IRIS H.-R. JIANG Detecting Negative Cycles by Bellman-Ford ¨ Augmented graph G’ of G 1. Add new node t 2. Connect all nodes to t with 0-cost edge ¨ G has a negative cycle iff G’ has a negative cycle reaching t ¨ Check if OPT(n, v) = OPT(n-1, v): ¤ If yes, no negative cycles ¤ If no, then extract cycle from shortest path from v to t ¨ Procedure: ¤ Build the augmented graph G’ for G ¤ Run Bellman-Ford on G’ for n iterations (instead of n-1). ¤ Upon termination, Bellman-Ford successor variables trace a negative cycle if one exists. Dynamic programming 51 t 0 0 0 0 0 Q: Why? Richard E. Bellman, 1962 Traveling Salesman Problem 52 Dynamic programming R. Bellman, Dynamic programming treatment of the travelling salesman problem. J. ACM 9, 1, Jan. 1962, pp. 61-63.
- 52. IRIS H.-R. JIANG Application: Currency Conversion (2/2) ¨ Product of edge costs on a cycle C = v1, v2, …, v1 ¤ rv1v2*rv2v3*…*rvnv1 ¤ Arbitrage: rv1v2*rv2v3*…*rvnv1>1 ¨ Sum of edge costs on a cycle C = v1, v2, …, v1 ¤ cv1v2+cv2v3+…+cvnv1 ¤ cuv = - lg ruv Arbitrage Negative cycle 49 Dynamic programming G £ F E ¥ $ 0.003065 455.2 208.1 0.004816 2.1904 1.3941 0.6677 327.25 129.52 0.008309 1.0752 $ 1.3941 F 0.6677 E 1.0752 -0.4793 0.5827 -0.1046 -0.4793+0.5827-0.1046 < 0 Arbitrage = negative cycle IRIS H.-R. JIANG Negative Cycle Detection ¨ If OPT(n, v) = OPT(n-1, v) for all v, then no negative cycles. ¤ Bellman-Ford: OPT(i, v) = OPT(n-1, v) for all v and i ³ n. ¨ If OPT(n, v) < OPT(n-1, v) for some v, then shortest path contains a negative cycle ¨ Pf: by contradiction ¤ Since OPT(n, v) < OPT(n-1, v), P has exactly n edges. ¤ Every path using at most n-1 edges costs more than P. ¤ (By pigeonhole principle,) P must contain a cycle C. ¤ If C were not a negative cycle, deleting C yields a v-t path with < n edges and no greater cost. ®¬ Dynamic programming 50 w v t C c(C) ³ 0 w v t C c(C) < 0 IRIS H.-R. JIANG Detecting Negative Cycles by Bellman-Ford ¨ Augmented graph G’ of G 1. Add new node t 2. Connect all nodes to t with 0-cost edge ¨ G has a negative cycle iff G’ has a negative cycle reaching t ¨ Check if OPT(n, v) = OPT(n-1, v): ¤ If yes, no negative cycles ¤ If no, then extract cycle from shortest path from v to t ¨ Procedure: ¤ Build the augmented graph G’ for G ¤ Run Bellman-Ford on G’ for n iterations (instead of n-1). ¤ Upon termination, Bellman-Ford successor variables trace a negative cycle if one exists. Dynamic programming 51 t 0 0 0 0 0 Q: Why? Richard E. Bellman, 1962 Traveling Salesman Problem 52 Dynamic programming R. Bellman, Dynamic programming treatment of the travelling salesman problem. J. ACM 9, 1, Jan. 1962, pp. 61-63.
- 53. IRIS H.-R. JIANG Travelling Salesman Problem ¨ TSP: A salesman is required to visit once and only once each of n different cities starting from a base city, and returning to this city. What path minimizes the total distance travelled by the salesman? ¤ The distance between each pair of cities is given ¨ TSP contest ¤ http://www.tsp.gatech.edu ¨ Brute-Force ¤ Try all permutations: O(n!) Dynamic programming 53 The Florida Sun-Sentinel, 20 Dec. 1998. IRIS H.-R. JIANG Dynamic Programming ¨ For each subset S of the cities with |S| ³ 2 and each u, vÎS, OPT(S, u, v) = the length of the shortest path that starts at u, ends at v, visits all cities in S ¨ Recurrence ¤ Case 1: S = {u, v} n OPT(S, u, v) = d(u, v) ¤ Case 2: |S| > 2 n Assume w Î S – {u, v} is visited first: OPT(S, u, v) = d(u, w) + OPT(S-u, w, v) n OPT(S, u, v) = minwÎS–{u,v}{d(u, w) + OPT(S-u, w, v)} ¨ Efficiency ¤ Space: O(2nn2) ¤ Running time: O(2nn3) n Although much better thatn O(n!), DP is suitable when the number of subproblems is polynomial. Dynamic programming 54 v u S u v w S-{u} IRIS H.-R. JIANG Summary: Dynamic Programming ¨ Smart recursion: In a nutshell, dynamic programming is recursion without repetition. ¤ Dynamic programming is NOT about filling in tables; it’s about smart recursion. ¤ Dynamic programming algorithms store the solutions of intermediate subproblems often but not always in some kind of array or table. ¤ A common mistake: focusing on the table (because tables are easy and familiar) instead of the much more important (and difficult) task of finding a correct recurrence. ¨ If the recurrence is wrong, or if we try to build up answers in the wrong order, the algorithm will NOT work! Dynamic programming 55 Courtesy of Prof. Jeff Erickson @ UIUC IRIS H.-R. JIANG Summary: Algorithmic Paradigms ¨ Brute-force (Exhaustive): Examine the entire set of possible solutions explicitly ¤ A victim to show the efficiencies of the following methods ¨ Greedy: Build up a solution incrementally, myopically optimizing some local criterion. ¤ Optimization problems that can be solved correctly by a greedy algorithm are very rare. ¨ Divide-and-conquer: Break up a problem into two sub- problems, solve each sub-problem independently, and combine solution to sub-problems to form solution to original problem. ¨ Dynamic programming: Break up a problem into a series of overlapping sub-problems, and build up solutions to larger and larger sub-problems. Dynamic programming 56
- 54. IRIS H.-R. JIANG Travelling Salesman Problem ¨ TSP: A salesman is required to visit once and only once each of n different cities starting from a base city, and returning to this city. What path minimizes the total distance travelled by the salesman? ¤ The distance between each pair of cities is given ¨ TSP contest ¤ http://www.tsp.gatech.edu ¨ Brute-Force ¤ Try all permutations: O(n!) Dynamic programming 53 The Florida Sun-Sentinel, 20 Dec. 1998. IRIS H.-R. JIANG Dynamic Programming ¨ For each subset S of the cities with |S| ³ 2 and each u, vÎS, OPT(S, u, v) = the length of the shortest path that starts at u, ends at v, visits all cities in S ¨ Recurrence ¤ Case 1: S = {u, v} n OPT(S, u, v) = d(u, v) ¤ Case 2: |S| > 2 n Assume w Î S – {u, v} is visited first: OPT(S, u, v) = d(u, w) + OPT(S-u, w, v) n OPT(S, u, v) = minwÎS–{u,v}{d(u, w) + OPT(S-u, w, v)} ¨ Efficiency ¤ Space: O(2nn2) ¤ Running time: O(2nn3) n Although much better thatn O(n!), DP is suitable when the number of subproblems is polynomial. Dynamic programming 54 v u S u v w S-{u} IRIS H.-R. JIANG Summary: Dynamic Programming ¨ Smart recursion: In a nutshell, dynamic programming is recursion without repetition. ¤ Dynamic programming is NOT about filling in tables; it’s about smart recursion. ¤ Dynamic programming algorithms store the solutions of intermediate subproblems often but not always in some kind of array or table. ¤ A common mistake: focusing on the table (because tables are easy and familiar) instead of the much more important (and difficult) task of finding a correct recurrence. ¨ If the recurrence is wrong, or if we try to build up answers in the wrong order, the algorithm will NOT work! Dynamic programming 55 Courtesy of Prof. Jeff Erickson @ UIUC IRIS H.-R. JIANG Summary: Algorithmic Paradigms ¨ Brute-force (Exhaustive): Examine the entire set of possible solutions explicitly ¤ A victim to show the efficiencies of the following methods ¨ Greedy: Build up a solution incrementally, myopically optimizing some local criterion. ¤ Optimization problems that can be solved correctly by a greedy algorithm are very rare. ¨ Divide-and-conquer: Break up a problem into two sub- problems, solve each sub-problem independently, and combine solution to sub-problems to form solution to original problem. ¨ Dynamic programming: Break up a problem into a series of overlapping sub-problems, and build up solutions to larger and larger sub-problems. Dynamic programming 56
- 55. IRIS H.-R. JIANG Travelling Salesman Problem ¨ TSP: A salesman is required to visit once and only once each of n different cities starting from a base city, and returning to this city. What path minimizes the total distance travelled by the salesman? ¤ The distance between each pair of cities is given ¨ TSP contest ¤ http://www.tsp.gatech.edu ¨ Brute-Force ¤ Try all permutations: O(n!) Dynamic programming 53 The Florida Sun-Sentinel, 20 Dec. 1998. IRIS H.-R. JIANG Dynamic Programming ¨ For each subset S of the cities with |S| ³ 2 and each u, vÎS, OPT(S, u, v) = the length of the shortest path that starts at u, ends at v, visits all cities in S ¨ Recurrence ¤ Case 1: S = {u, v} n OPT(S, u, v) = d(u, v) ¤ Case 2: |S| > 2 n Assume w Î S – {u, v} is visited first: OPT(S, u, v) = d(u, w) + OPT(S-u, w, v) n OPT(S, u, v) = minwÎS–{u,v}{d(u, w) + OPT(S-u, w, v)} ¨ Efficiency ¤ Space: O(2nn2) ¤ Running time: O(2nn3) n Although much better thatn O(n!), DP is suitable when the number of subproblems is polynomial. Dynamic programming 54 v u S u v w S-{u} IRIS H.-R. JIANG Summary: Dynamic Programming ¨ Smart recursion: In a nutshell, dynamic programming is recursion without repetition. ¤ Dynamic programming is NOT about filling in tables; it’s about smart recursion. ¤ Dynamic programming algorithms store the solutions of intermediate subproblems often but not always in some kind of array or table. ¤ A common mistake: focusing on the table (because tables are easy and familiar) instead of the much more important (and difficult) task of finding a correct recurrence. ¨ If the recurrence is wrong, or if we try to build up answers in the wrong order, the algorithm will NOT work! Dynamic programming 55 Courtesy of Prof. Jeff Erickson @ UIUC IRIS H.-R. JIANG Summary: Algorithmic Paradigms ¨ Brute-force (Exhaustive): Examine the entire set of possible solutions explicitly ¤ A victim to show the efficiencies of the following methods ¨ Greedy: Build up a solution incrementally, myopically optimizing some local criterion. ¤ Optimization problems that can be solved correctly by a greedy algorithm are very rare. ¨ Divide-and-conquer: Break up a problem into two sub- problems, solve each sub-problem independently, and combine solution to sub-problems to form solution to original problem. ¨ Dynamic programming: Break up a problem into a series of overlapping sub-problems, and build up solutions to larger and larger sub-problems. Dynamic programming 56
- 56. IRIS H.-R. JIANG Travelling Salesman Problem ¨ TSP: A salesman is required to visit once and only once each of n different cities starting from a base city, and returning to this city. What path minimizes the total distance travelled by the salesman? ¤ The distance between each pair of cities is given ¨ TSP contest ¤ http://www.tsp.gatech.edu ¨ Brute-Force ¤ Try all permutations: O(n!) Dynamic programming 53 The Florida Sun-Sentinel, 20 Dec. 1998. IRIS H.-R. JIANG Dynamic Programming ¨ For each subset S of the cities with |S| ³ 2 and each u, vÎS, OPT(S, u, v) = the length of the shortest path that starts at u, ends at v, visits all cities in S ¨ Recurrence ¤ Case 1: S = {u, v} n OPT(S, u, v) = d(u, v) ¤ Case 2: |S| > 2 n Assume w Î S – {u, v} is visited first: OPT(S, u, v) = d(u, w) + OPT(S-u, w, v) n OPT(S, u, v) = minwÎS–{u,v}{d(u, w) + OPT(S-u, w, v)} ¨ Efficiency ¤ Space: O(2nn2) ¤ Running time: O(2nn3) n Although much better thatn O(n!), DP is suitable when the number of subproblems is polynomial. Dynamic programming 54 v u S u v w S-{u} IRIS H.-R. JIANG Summary: Dynamic Programming ¨ Smart recursion: In a nutshell, dynamic programming is recursion without repetition. ¤ Dynamic programming is NOT about filling in tables; it’s about smart recursion. ¤ Dynamic programming algorithms store the solutions of intermediate subproblems often but not always in some kind of array or table. ¤ A common mistake: focusing on the table (because tables are easy and familiar) instead of the much more important (and difficult) task of finding a correct recurrence. ¨ If the recurrence is wrong, or if we try to build up answers in the wrong order, the algorithm will NOT work! Dynamic programming 55 Courtesy of Prof. Jeff Erickson @ UIUC IRIS H.-R. JIANG Summary: Algorithmic Paradigms ¨ Brute-force (Exhaustive): Examine the entire set of possible solutions explicitly ¤ A victim to show the efficiencies of the following methods ¨ Greedy: Build up a solution incrementally, myopically optimizing some local criterion. ¤ Optimization problems that can be solved correctly by a greedy algorithm are very rare. ¨ Divide-and-conquer: Break up a problem into two sub- problems, solve each sub-problem independently, and combine solution to sub-problems to form solution to original problem. ¨ Dynamic programming: Break up a problem into a series of overlapping sub-problems, and build up solutions to larger and larger sub-problems. Dynamic programming 56









![IRIS H.-R. JIANG
Designing a Recursive Algorithm (2/3)
¨ Second attempt: Induction on interval index
¤ First of all, sort intervals in ascending order of finish times
¤ In fact, this is also a trick for DP
¨ p(j) is the largest index i < j s.t. intervals i and j are disjoint
¤ p(j) = 0 if no request i < j is disjoint from j
Dynamic programming
9
1
2
2
4
4
7
p(1) = 0
p(2) = 0
p(3) = 1
p(4) = 0
p(5) = 3
p(6) = 3
1
2
3
4
5
6
p(2) = 0
p(6) = 3
4
1
4
IRIS H.-R. JIANG
Designing a Recursive Algorithm (3/3)
¨ Oj = the optimal solution for intervals 1, …, j
¨ OPT(j) = the value of the optimal solution for intervals 1, …, j
¤ e.g., O6 = ? Include interval 6 or not?
n Þ O6 = {6, O3} or O5
n OPT(6) = max{{v6+OPT(3)}, OPT(5)}
¤ OPT(j) = max{{vj+OPT(p(j))}, OPT(j-1)}
Dynamic programming
10
1
2
2
4
4
7
p(1) = 0
p(2) = 0
p(3) = 1
p(4) = 0
p(5) = 3
p(6) = 3
1
2
3
4
5
6 1
IRIS H.-R. JIANG
Direct Implementation
Dynamic programming
11
// Preprocessing:
// 1. Sort intervals by finish times: f1 £ f2 £ ... £ fn
// 2. Compute p(1), p(2), …, p(n)
Compute-Opt(j)
1. if (j = 0) then return 0
2. else return max{{vj+Compute-Opt(p(j))}, Compute-Opt(j-1)}
OPT(j) = max{{vj+OPT(p(j))}, OPT(j-1)}
5
4
3
1
2
1
3
2 1
1
6
3
2 1
1
The tree of calls widens very quickly
due to recursive branching!
1
2
2
4
4
7
p(1) = 0
p(2) = 0
p(3) = 1
p(4) = 0
p(5) = 3
p(6) = 3
IRIS H.-R. JIANG
Memoization: Top-Down
¨ The tree of calls widens very quickly due to recursive
branching!
¤ e.g., exponential running time when p(j) = j – 2 for all j
¨ Q: What’s wrong? A: Redundant calls!
¨ Q: How to eliminate this redundancy?
¨ A: Store the value for future! (memoization)
Dynamic programming
12
5
4
3
1
2
1
3
2 1
1
6
3
2 1
1
3
1
2
1
3
2 1
1
3
2 1
1
M-Compute-Opt(j)
1. if (j = 0) then return 0
2. else if (M[j] is not empty) then return M[j]
3. else return M[j] = max{{vj+M-Compute-Opt(p(j))},
M-Compute-Opt(j-1)}
Running time:
O(n)
How to report the
optimal solution O?
5
4
3
2
1
6](https://image.slidesharecdn.com/algorithm6dynamicprogramming-220522073057-711c84d9/85/algorithm_6dynamic_programming-pdf-9-320.jpg)
![IRIS H.-R. JIANG
Designing a Recursive Algorithm (2/3)
¨ Second attempt: Induction on interval index
¤ First of all, sort intervals in ascending order of finish times
¤ In fact, this is also a trick for DP
¨ p(j) is the largest index i < j s.t. intervals i and j are disjoint
¤ p(j) = 0 if no request i < j is disjoint from j
Dynamic programming
9
1
2
2
4
4
7
p(1) = 0
p(2) = 0
p(3) = 1
p(4) = 0
p(5) = 3
p(6) = 3
1
2
3
4
5
6
p(2) = 0
p(6) = 3
4
1
4
IRIS H.-R. JIANG
Designing a Recursive Algorithm (3/3)
¨ Oj = the optimal solution for intervals 1, …, j
¨ OPT(j) = the value of the optimal solution for intervals 1, …, j
¤ e.g., O6 = ? Include interval 6 or not?
n Þ O6 = {6, O3} or O5
n OPT(6) = max{{v6+OPT(3)}, OPT(5)}
¤ OPT(j) = max{{vj+OPT(p(j))}, OPT(j-1)}
Dynamic programming
10
1
2
2
4
4
7
p(1) = 0
p(2) = 0
p(3) = 1
p(4) = 0
p(5) = 3
p(6) = 3
1
2
3
4
5
6 1
IRIS H.-R. JIANG
Direct Implementation
Dynamic programming
11
// Preprocessing:
// 1. Sort intervals by finish times: f1 £ f2 £ ... £ fn
// 2. Compute p(1), p(2), …, p(n)
Compute-Opt(j)
1. if (j = 0) then return 0
2. else return max{{vj+Compute-Opt(p(j))}, Compute-Opt(j-1)}
OPT(j) = max{{vj+OPT(p(j))}, OPT(j-1)}
5
4
3
1
2
1
3
2 1
1
6
3
2 1
1
The tree of calls widens very quickly
due to recursive branching!
1
2
2
4
4
7
p(1) = 0
p(2) = 0
p(3) = 1
p(4) = 0
p(5) = 3
p(6) = 3
IRIS H.-R. JIANG
Memoization: Top-Down
¨ The tree of calls widens very quickly due to recursive
branching!
¤ e.g., exponential running time when p(j) = j – 2 for all j
¨ Q: What’s wrong? A: Redundant calls!
¨ Q: How to eliminate this redundancy?
¨ A: Store the value for future! (memoization)
Dynamic programming
12
5
4
3
1
2
1
3
2 1
1
6
3
2 1
1
3
1
2
1
3
2 1
1
3
2 1
1
M-Compute-Opt(j)
1. if (j = 0) then return 0
2. else if (M[j] is not empty) then return M[j]
3. else return M[j] = max{{vj+M-Compute-Opt(p(j))},
M-Compute-Opt(j-1)}
Running time:
O(n)
How to report the
optimal solution O?
5
4
3
2
1
6](https://image.slidesharecdn.com/algorithm6dynamicprogramming-220522073057-711c84d9/85/algorithm_6dynamic_programming-pdf-10-320.jpg)
![IRIS H.-R. JIANG
Designing a Recursive Algorithm (2/3)
¨ Second attempt: Induction on interval index
¤ First of all, sort intervals in ascending order of finish times
¤ In fact, this is also a trick for DP
¨ p(j) is the largest index i < j s.t. intervals i and j are disjoint
¤ p(j) = 0 if no request i < j is disjoint from j
Dynamic programming
9
1
2
2
4
4
7
p(1) = 0
p(2) = 0
p(3) = 1
p(4) = 0
p(5) = 3
p(6) = 3
1
2
3
4
5
6
p(2) = 0
p(6) = 3
4
1
4
IRIS H.-R. JIANG
Designing a Recursive Algorithm (3/3)
¨ Oj = the optimal solution for intervals 1, …, j
¨ OPT(j) = the value of the optimal solution for intervals 1, …, j
¤ e.g., O6 = ? Include interval 6 or not?
n Þ O6 = {6, O3} or O5
n OPT(6) = max{{v6+OPT(3)}, OPT(5)}
¤ OPT(j) = max{{vj+OPT(p(j))}, OPT(j-1)}
Dynamic programming
10
1
2
2
4
4
7
p(1) = 0
p(2) = 0
p(3) = 1
p(4) = 0
p(5) = 3
p(6) = 3
1
2
3
4
5
6 1
IRIS H.-R. JIANG
Direct Implementation
Dynamic programming
11
// Preprocessing:
// 1. Sort intervals by finish times: f1 £ f2 £ ... £ fn
// 2. Compute p(1), p(2), …, p(n)
Compute-Opt(j)
1. if (j = 0) then return 0
2. else return max{{vj+Compute-Opt(p(j))}, Compute-Opt(j-1)}
OPT(j) = max{{vj+OPT(p(j))}, OPT(j-1)}
5
4
3
1
2
1
3
2 1
1
6
3
2 1
1
The tree of calls widens very quickly
due to recursive branching!
1
2
2
4
4
7
p(1) = 0
p(2) = 0
p(3) = 1
p(4) = 0
p(5) = 3
p(6) = 3
IRIS H.-R. JIANG
Memoization: Top-Down
¨ The tree of calls widens very quickly due to recursive
branching!
¤ e.g., exponential running time when p(j) = j – 2 for all j
¨ Q: What’s wrong? A: Redundant calls!
¨ Q: How to eliminate this redundancy?
¨ A: Store the value for future! (memoization)
Dynamic programming
12
5
4
3
1
2
1
3
2 1
1
6
3
2 1
1
3
1
2
1
3
2 1
1
3
2 1
1
M-Compute-Opt(j)
1. if (j = 0) then return 0
2. else if (M[j] is not empty) then return M[j]
3. else return M[j] = max{{vj+M-Compute-Opt(p(j))},
M-Compute-Opt(j-1)}
Running time:
O(n)
How to report the
optimal solution O?
5
4
3
2
1
6](https://image.slidesharecdn.com/algorithm6dynamicprogramming-220522073057-711c84d9/85/algorithm_6dynamic_programming-pdf-11-320.jpg)
![IRIS H.-R. JIANG
Designing a Recursive Algorithm (2/3)
¨ Second attempt: Induction on interval index
¤ First of all, sort intervals in ascending order of finish times
¤ In fact, this is also a trick for DP
¨ p(j) is the largest index i < j s.t. intervals i and j are disjoint
¤ p(j) = 0 if no request i < j is disjoint from j
Dynamic programming
9
1
2
2
4
4
7
p(1) = 0
p(2) = 0
p(3) = 1
p(4) = 0
p(5) = 3
p(6) = 3
1
2
3
4
5
6
p(2) = 0
p(6) = 3
4
1
4
IRIS H.-R. JIANG
Designing a Recursive Algorithm (3/3)
¨ Oj = the optimal solution for intervals 1, …, j
¨ OPT(j) = the value of the optimal solution for intervals 1, …, j
¤ e.g., O6 = ? Include interval 6 or not?
n Þ O6 = {6, O3} or O5
n OPT(6) = max{{v6+OPT(3)}, OPT(5)}
¤ OPT(j) = max{{vj+OPT(p(j))}, OPT(j-1)}
Dynamic programming
10
1
2
2
4
4
7
p(1) = 0
p(2) = 0
p(3) = 1
p(4) = 0
p(5) = 3
p(6) = 3
1
2
3
4
5
6 1
IRIS H.-R. JIANG
Direct Implementation
Dynamic programming
11
// Preprocessing:
// 1. Sort intervals by finish times: f1 £ f2 £ ... £ fn
// 2. Compute p(1), p(2), …, p(n)
Compute-Opt(j)
1. if (j = 0) then return 0
2. else return max{{vj+Compute-Opt(p(j))}, Compute-Opt(j-1)}
OPT(j) = max{{vj+OPT(p(j))}, OPT(j-1)}
5
4
3
1
2
1
3
2 1
1
6
3
2 1
1
The tree of calls widens very quickly
due to recursive branching!
1
2
2
4
4
7
p(1) = 0
p(2) = 0
p(3) = 1
p(4) = 0
p(5) = 3
p(6) = 3
IRIS H.-R. JIANG
Memoization: Top-Down
¨ The tree of calls widens very quickly due to recursive
branching!
¤ e.g., exponential running time when p(j) = j – 2 for all j
¨ Q: What’s wrong? A: Redundant calls!
¨ Q: How to eliminate this redundancy?
¨ A: Store the value for future! (memoization)
Dynamic programming
12
5
4
3
1
2
1
3
2 1
1
6
3
2 1
1
3
1
2
1
3
2 1
1
3
2 1
1
M-Compute-Opt(j)
1. if (j = 0) then return 0
2. else if (M[j] is not empty) then return M[j]
3. else return M[j] = max{{vj+M-Compute-Opt(p(j))},
M-Compute-Opt(j-1)}
Running time:
O(n)
How to report the
optimal solution O?
5
4
3
2
1
6](https://image.slidesharecdn.com/algorithm6dynamicprogramming-220522073057-711c84d9/85/algorithm_6dynamic_programming-pdf-12-320.jpg)
![IRIS H.-R. JIANG
Iteration: Bottom-Up
¨ We can also compute the array M[j] by an iterative algorithm.
Dynamic programming
13
I-Compute-Opt
1. M[0] = 0
2. for j = 1, 2, .., n do
3. M[j] = max{vj+M[p(j)], M[j-1]}
Running time:
O(n)
1
2
2
4
4
7
p(1) = 0
p(2) = 0
p(3) = 1
p(4) = 0
p(5) = 3
p(6) = 3
1
2
3
4
5
6
0 2 4
0 2 4 6
0 2 4 6 7
0 2 4 6 7 8
0 2 4 6 7 8 8
M =
0 1 2 3 4 5
0
6
0 2
max{4+0, 2}
IRIS H.-R. JIANG
Summary: Memoization vs. Iteration
¨ Top-down
¨ An recursive algorithm
¤ Compute only what we need
¨ Bottom-up
¨ An iterative algorithm
¤ Construct solutions from the
smallest subproblem to the
largest one
¤ Compute every small piece
Memoization Iteration
14
Dynamic programming
The running time and
memory requirement highly
depend on the table size
Start with the recursive
divide-and-conquer
algorithm
IRIS H.-R. JIANG
Keys for Dynamic Programming
¨ Dynamic programming can be used if the problem satisfies the
following properties:
¤ There are only a polynomial number of subproblems
¤ The solution to the original problem can be easily computed from
the solutions to the subproblems
¤ There is a natural ordering on subproblems from “smallest” to
“largest,” together with an easy-to-compute recurrence
Dynamic programming
15
5
4
3
1
2
1
3
2 1
1
6
3
2 1
1
3
1
2
1
3
2 1
1
3
2 1
1
5
4
3
2
1
6
IRIS H.-R. JIANG
Keys for Dynamic Programming
¨ DP typically is applied to optimization problems.
¨ DP works best on objects that are linearly ordered an cannot be
rearranged
¨ Elements of DP
¤ Optimal substructure: an optimal solution contains within its
optimal solutions to subproblems.
¤ Overlapping subproblem: a recursive algorithm revisits the same
problem over and over again; typically, the total number of distinct
subproblems is a polynomial in the input size.
Dynamic programming
16
Cormen, Leiserson, Rivest, Stein, Introduction to Algorithms,
2nd Ed., McGraw Hill/MIT Press, 2001
5
4
3
1
2
1
3
2 1
1
6
3
2 1
1
3
1
2
1
3
2 1
1
3
2 1
1
5
4
3
2
1
6
In optimization problems, we
are interested in finding a thing
which maximizes or minimizes
some function.](https://image.slidesharecdn.com/algorithm6dynamicprogramming-220522073057-711c84d9/85/algorithm_6dynamic_programming-pdf-13-320.jpg)
![IRIS H.-R. JIANG
Iteration: Bottom-Up
¨ We can also compute the array M[j] by an iterative algorithm.
Dynamic programming
13
I-Compute-Opt
1. M[0] = 0
2. for j = 1, 2, .., n do
3. M[j] = max{vj+M[p(j)], M[j-1]}
Running time:
O(n)
1
2
2
4
4
7
p(1) = 0
p(2) = 0
p(3) = 1
p(4) = 0
p(5) = 3
p(6) = 3
1
2
3
4
5
6
0 2 4
0 2 4 6
0 2 4 6 7
0 2 4 6 7 8
0 2 4 6 7 8 8
M =
0 1 2 3 4 5
0
6
0 2
max{4+0, 2}
IRIS H.-R. JIANG
Summary: Memoization vs. Iteration
¨ Top-down
¨ An recursive algorithm
¤ Compute only what we need
¨ Bottom-up
¨ An iterative algorithm
¤ Construct solutions from the
smallest subproblem to the
largest one
¤ Compute every small piece
Memoization Iteration
14
Dynamic programming
The running time and
memory requirement highly
depend on the table size
Start with the recursive
divide-and-conquer
algorithm
IRIS H.-R. JIANG
Keys for Dynamic Programming
¨ Dynamic programming can be used if the problem satisfies the
following properties:
¤ There are only a polynomial number of subproblems
¤ The solution to the original problem can be easily computed from
the solutions to the subproblems
¤ There is a natural ordering on subproblems from “smallest” to
“largest,” together with an easy-to-compute recurrence
Dynamic programming
15
5
4
3
1
2
1
3
2 1
1
6
3
2 1
1
3
1
2
1
3
2 1
1
3
2 1
1
5
4
3
2
1
6
IRIS H.-R. JIANG
Keys for Dynamic Programming
¨ DP typically is applied to optimization problems.
¨ DP works best on objects that are linearly ordered an cannot be
rearranged
¨ Elements of DP
¤ Optimal substructure: an optimal solution contains within its
optimal solutions to subproblems.
¤ Overlapping subproblem: a recursive algorithm revisits the same
problem over and over again; typically, the total number of distinct
subproblems is a polynomial in the input size.
Dynamic programming
16
Cormen, Leiserson, Rivest, Stein, Introduction to Algorithms,
2nd Ed., McGraw Hill/MIT Press, 2001
5
4
3
1
2
1
3
2 1
1
6
3
2 1
1
3
1
2
1
3
2 1
1
3
2 1
1
5
4
3
2
1
6
In optimization problems, we
are interested in finding a thing
which maximizes or minimizes
some function.](https://image.slidesharecdn.com/algorithm6dynamicprogramming-220522073057-711c84d9/85/algorithm_6dynamic_programming-pdf-14-320.jpg)
![IRIS H.-R. JIANG
Iteration: Bottom-Up
¨ We can also compute the array M[j] by an iterative algorithm.
Dynamic programming
13
I-Compute-Opt
1. M[0] = 0
2. for j = 1, 2, .., n do
3. M[j] = max{vj+M[p(j)], M[j-1]}
Running time:
O(n)
1
2
2
4
4
7
p(1) = 0
p(2) = 0
p(3) = 1
p(4) = 0
p(5) = 3
p(6) = 3
1
2
3
4
5
6
0 2 4
0 2 4 6
0 2 4 6 7
0 2 4 6 7 8
0 2 4 6 7 8 8
M =
0 1 2 3 4 5
0
6
0 2
max{4+0, 2}
IRIS H.-R. JIANG
Summary: Memoization vs. Iteration
¨ Top-down
¨ An recursive algorithm
¤ Compute only what we need
¨ Bottom-up
¨ An iterative algorithm
¤ Construct solutions from the
smallest subproblem to the
largest one
¤ Compute every small piece
Memoization Iteration
14
Dynamic programming
The running time and
memory requirement highly
depend on the table size
Start with the recursive
divide-and-conquer
algorithm
IRIS H.-R. JIANG
Keys for Dynamic Programming
¨ Dynamic programming can be used if the problem satisfies the
following properties:
¤ There are only a polynomial number of subproblems
¤ The solution to the original problem can be easily computed from
the solutions to the subproblems
¤ There is a natural ordering on subproblems from “smallest” to
“largest,” together with an easy-to-compute recurrence
Dynamic programming
15
5
4
3
1
2
1
3
2 1
1
6
3
2 1
1
3
1
2
1
3
2 1
1
3
2 1
1
5
4
3
2
1
6
IRIS H.-R. JIANG
Keys for Dynamic Programming
¨ DP typically is applied to optimization problems.
¨ DP works best on objects that are linearly ordered an cannot be
rearranged
¨ Elements of DP
¤ Optimal substructure: an optimal solution contains within its
optimal solutions to subproblems.
¤ Overlapping subproblem: a recursive algorithm revisits the same
problem over and over again; typically, the total number of distinct
subproblems is a polynomial in the input size.
Dynamic programming
16
Cormen, Leiserson, Rivest, Stein, Introduction to Algorithms,
2nd Ed., McGraw Hill/MIT Press, 2001
5
4
3
1
2
1
3
2 1
1
6
3
2 1
1
3
1
2
1
3
2 1
1
3
2 1
1
5
4
3
2
1
6
In optimization problems, we
are interested in finding a thing
which maximizes or minimizes
some function.](https://image.slidesharecdn.com/algorithm6dynamicprogramming-220522073057-711c84d9/85/algorithm_6dynamic_programming-pdf-15-320.jpg)
![IRIS H.-R. JIANG
Iteration: Bottom-Up
¨ We can also compute the array M[j] by an iterative algorithm.
Dynamic programming
13
I-Compute-Opt
1. M[0] = 0
2. for j = 1, 2, .., n do
3. M[j] = max{vj+M[p(j)], M[j-1]}
Running time:
O(n)
1
2
2
4
4
7
p(1) = 0
p(2) = 0
p(3) = 1
p(4) = 0
p(5) = 3
p(6) = 3
1
2
3
4
5
6
0 2 4
0 2 4 6
0 2 4 6 7
0 2 4 6 7 8
0 2 4 6 7 8 8
M =
0 1 2 3 4 5
0
6
0 2
max{4+0, 2}
IRIS H.-R. JIANG
Summary: Memoization vs. Iteration
¨ Top-down
¨ An recursive algorithm
¤ Compute only what we need
¨ Bottom-up
¨ An iterative algorithm
¤ Construct solutions from the
smallest subproblem to the
largest one
¤ Compute every small piece
Memoization Iteration
14
Dynamic programming
The running time and
memory requirement highly
depend on the table size
Start with the recursive
divide-and-conquer
algorithm
IRIS H.-R. JIANG
Keys for Dynamic Programming
¨ Dynamic programming can be used if the problem satisfies the
following properties:
¤ There are only a polynomial number of subproblems
¤ The solution to the original problem can be easily computed from
the solutions to the subproblems
¤ There is a natural ordering on subproblems from “smallest” to
“largest,” together with an easy-to-compute recurrence
Dynamic programming
15
5
4
3
1
2
1
3
2 1
1
6
3
2 1
1
3
1
2
1
3
2 1
1
3
2 1
1
5
4
3
2
1
6
IRIS H.-R. JIANG
Keys for Dynamic Programming
¨ DP typically is applied to optimization problems.
¨ DP works best on objects that are linearly ordered an cannot be
rearranged
¨ Elements of DP
¤ Optimal substructure: an optimal solution contains within its
optimal solutions to subproblems.
¤ Overlapping subproblem: a recursive algorithm revisits the same
problem over and over again; typically, the total number of distinct
subproblems is a polynomial in the input size.
Dynamic programming
16
Cormen, Leiserson, Rivest, Stein, Introduction to Algorithms,
2nd Ed., McGraw Hill/MIT Press, 2001
5
4
3
1
2
1
3
2 1
1
6
3
2 1
1
3
1
2
1
3
2 1
1
3
2 1
1
5
4
3
2
1
6
In optimization problems, we
are interested in finding a thing
which maximizes or minimizes
some function.](https://image.slidesharecdn.com/algorithm6dynamicprogramming-220522073057-711c84d9/85/algorithm_6dynamic_programming-pdf-16-320.jpg)




![IRIS H.-R. JIANG
What’s Wrong?
¨ What if we call fib(5)?
¤ fib(5)
¤ fib(4) + fib(3)
¤ (fib(3) + fib(2)) + (fib(2) + fib(1))
¤ ((fib(2) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))
¤ (((fib(1) + fib(0)) + fib(1))+(fib(1) + fib(0)))+((fib(1) + fib(0))+fib(1))
¤ A call tree that calls the function on the same value many
different times
n fib(2) was calculated three times from scratch
n Impractical for large n
Dynamic programming
21
fib(n)
1. if n £ 1 return n
2. return fib(n ! 1) + fib(n ! 2)
5
4
3
2
3
2 1
2
1 0 1 0
1
1 0
2
1 0
2
1 0
2
1 0
IRIS H.-R. JIANG
Too Many Redundant Calls!
¨ How to remove redundancy?
¤ Prevent repeated calculation
Recursion True dependency
Dynamic programming
22
5
4 3
2 1
5
4
3
2
3
2 1
2
1 0 1 0
1
1 0
3
2
3
1
2
1 0
1
1 0
2
1 0
2
1 0
2
1 0
IRIS H.-R. JIANG
Dynamic Programming -- Memoization
¨ Store the values in a table
¤ Check the table before a recursive call
¤ Top-down!
n The control flow is almost the same as the original one
Dynamic programming
23
fib(n)
1. Initialize f[0..n] with -1 // -1: unfilled
2. f[0] = 0; f[1] = 1
3. fibonacci(n, f)
fibonacci(n, f)
1. If f[n] == -1 then
2. f[n] = fibonacci(n ! 1, f) + fibonacci(n ! 2, f)
3. return f[n] // if f[n] already exists, directly return
5
4 3
2 1
IRIS H.-R. JIANG
Dynamic Programming -- Bottom-up?
¨ Store the values in a table
¤ Bottom-up
n Compute the values for small problems first
¤ Much like induction
Dynamic programming
24
fib(n)
1. initialize f[1..n] with -1 // -1: unfilled
2. f[0] = 0; f[1] = 1
3. for i=2 to n do
4. f[i] = f[i-1]+ f[i-2]
5. return f[n]
5
4 3
2 1](https://image.slidesharecdn.com/algorithm6dynamicprogramming-220522073057-711c84d9/85/algorithm_6dynamic_programming-pdf-21-320.jpg)
![IRIS H.-R. JIANG
What’s Wrong?
¨ What if we call fib(5)?
¤ fib(5)
¤ fib(4) + fib(3)
¤ (fib(3) + fib(2)) + (fib(2) + fib(1))
¤ ((fib(2) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))
¤ (((fib(1) + fib(0)) + fib(1))+(fib(1) + fib(0)))+((fib(1) + fib(0))+fib(1))
¤ A call tree that calls the function on the same value many
different times
n fib(2) was calculated three times from scratch
n Impractical for large n
Dynamic programming
21
fib(n)
1. if n £ 1 return n
2. return fib(n ! 1) + fib(n ! 2)
5
4
3
2
3
2 1
2
1 0 1 0
1
1 0
2
1 0
2
1 0
2
1 0
IRIS H.-R. JIANG
Too Many Redundant Calls!
¨ How to remove redundancy?
¤ Prevent repeated calculation
Recursion True dependency
Dynamic programming
22
5
4 3
2 1
5
4
3
2
3
2 1
2
1 0 1 0
1
1 0
3
2
3
1
2
1 0
1
1 0
2
1 0
2
1 0
2
1 0
IRIS H.-R. JIANG
Dynamic Programming -- Memoization
¨ Store the values in a table
¤ Check the table before a recursive call
¤ Top-down!
n The control flow is almost the same as the original one
Dynamic programming
23
fib(n)
1. Initialize f[0..n] with -1 // -1: unfilled
2. f[0] = 0; f[1] = 1
3. fibonacci(n, f)
fibonacci(n, f)
1. If f[n] == -1 then
2. f[n] = fibonacci(n ! 1, f) + fibonacci(n ! 2, f)
3. return f[n] // if f[n] already exists, directly return
5
4 3
2 1
IRIS H.-R. JIANG
Dynamic Programming -- Bottom-up?
¨ Store the values in a table
¤ Bottom-up
n Compute the values for small problems first
¤ Much like induction
Dynamic programming
24
fib(n)
1. initialize f[1..n] with -1 // -1: unfilled
2. f[0] = 0; f[1] = 1
3. for i=2 to n do
4. f[i] = f[i-1]+ f[i-2]
5. return f[n]
5
4 3
2 1](https://image.slidesharecdn.com/algorithm6dynamicprogramming-220522073057-711c84d9/85/algorithm_6dynamic_programming-pdf-22-320.jpg)
![IRIS H.-R. JIANG
What’s Wrong?
¨ What if we call fib(5)?
¤ fib(5)
¤ fib(4) + fib(3)
¤ (fib(3) + fib(2)) + (fib(2) + fib(1))
¤ ((fib(2) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))
¤ (((fib(1) + fib(0)) + fib(1))+(fib(1) + fib(0)))+((fib(1) + fib(0))+fib(1))
¤ A call tree that calls the function on the same value many
different times
n fib(2) was calculated three times from scratch
n Impractical for large n
Dynamic programming
21
fib(n)
1. if n £ 1 return n
2. return fib(n ! 1) + fib(n ! 2)
5
4
3
2
3
2 1
2
1 0 1 0
1
1 0
2
1 0
2
1 0
2
1 0
IRIS H.-R. JIANG
Too Many Redundant Calls!
¨ How to remove redundancy?
¤ Prevent repeated calculation
Recursion True dependency
Dynamic programming
22
5
4 3
2 1
5
4
3
2
3
2 1
2
1 0 1 0
1
1 0
3
2
3
1
2
1 0
1
1 0
2
1 0
2
1 0
2
1 0
IRIS H.-R. JIANG
Dynamic Programming -- Memoization
¨ Store the values in a table
¤ Check the table before a recursive call
¤ Top-down!
n The control flow is almost the same as the original one
Dynamic programming
23
fib(n)
1. Initialize f[0..n] with -1 // -1: unfilled
2. f[0] = 0; f[1] = 1
3. fibonacci(n, f)
fibonacci(n, f)
1. If f[n] == -1 then
2. f[n] = fibonacci(n ! 1, f) + fibonacci(n ! 2, f)
3. return f[n] // if f[n] already exists, directly return
5
4 3
2 1
IRIS H.-R. JIANG
Dynamic Programming -- Bottom-up?
¨ Store the values in a table
¤ Bottom-up
n Compute the values for small problems first
¤ Much like induction
Dynamic programming
24
fib(n)
1. initialize f[1..n] with -1 // -1: unfilled
2. f[0] = 0; f[1] = 1
3. for i=2 to n do
4. f[i] = f[i-1]+ f[i-2]
5. return f[n]
5
4 3
2 1](https://image.slidesharecdn.com/algorithm6dynamicprogramming-220522073057-711c84d9/85/algorithm_6dynamic_programming-pdf-23-320.jpg)
![IRIS H.-R. JIANG
What’s Wrong?
¨ What if we call fib(5)?
¤ fib(5)
¤ fib(4) + fib(3)
¤ (fib(3) + fib(2)) + (fib(2) + fib(1))
¤ ((fib(2) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))
¤ (((fib(1) + fib(0)) + fib(1))+(fib(1) + fib(0)))+((fib(1) + fib(0))+fib(1))
¤ A call tree that calls the function on the same value many
different times
n fib(2) was calculated three times from scratch
n Impractical for large n
Dynamic programming
21
fib(n)
1. if n £ 1 return n
2. return fib(n ! 1) + fib(n ! 2)
5
4
3
2
3
2 1
2
1 0 1 0
1
1 0
2
1 0
2
1 0
2
1 0
IRIS H.-R. JIANG
Too Many Redundant Calls!
¨ How to remove redundancy?
¤ Prevent repeated calculation
Recursion True dependency
Dynamic programming
22
5
4 3
2 1
5
4
3
2
3
2 1
2
1 0 1 0
1
1 0
3
2
3
1
2
1 0
1
1 0
2
1 0
2
1 0
2
1 0
IRIS H.-R. JIANG
Dynamic Programming -- Memoization
¨ Store the values in a table
¤ Check the table before a recursive call
¤ Top-down!
n The control flow is almost the same as the original one
Dynamic programming
23
fib(n)
1. Initialize f[0..n] with -1 // -1: unfilled
2. f[0] = 0; f[1] = 1
3. fibonacci(n, f)
fibonacci(n, f)
1. If f[n] == -1 then
2. f[n] = fibonacci(n ! 1, f) + fibonacci(n ! 2, f)
3. return f[n] // if f[n] already exists, directly return
5
4 3
2 1
IRIS H.-R. JIANG
Dynamic Programming -- Bottom-up?
¨ Store the values in a table
¤ Bottom-up
n Compute the values for small problems first
¤ Much like induction
Dynamic programming
24
fib(n)
1. initialize f[1..n] with -1 // -1: unfilled
2. f[0] = 0; f[1] = 1
3. for i=2 to n do
4. f[i] = f[i-1]+ f[i-2]
5. return f[n]
5
4 3
2 1](https://image.slidesharecdn.com/algorithm6dynamicprogramming-220522073057-711c84d9/85/algorithm_6dynamic_programming-pdf-24-320.jpg)

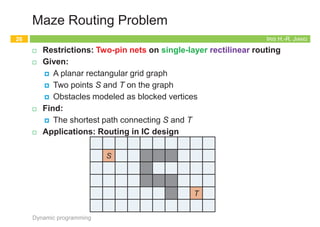






![IRIS H.-R. JIANG
DP: Iteration
Dynamic programming
33
OPT(i, w) = 0 if i, w = 0
OPT(i-1, w) if wi > w
max {OPT(i-1, w), wi + OPT(i-1, w-wi)} otherwise
Subset-sum(n, w1,…, wn, W)
1. for w = 0, 1, …, W do
2. M[0, w] = 0
3. for i = 0, 1, …, n do
4. M[i, 0] = 0
5. for i = 1, 2, .., n do
6. for w = 1, 2, .., W do
7. if (wi > w) then
8. M[i, w] = M[i-1, w]
9. else
10. M[i, w] = max {M[i-1, w], wi +M[i-1, w-wi]}
IRIS H.-R. JIANG
Example
Dynamic programming
34
1
Weight
5
6
2
7
Item
1
3
4
5
2
W = 11
0
0
0
0
0
0 0 0 0 0 0 0 0 0 0 0 0
1 2 3 3 3 3 3 3 3 3 3
1 2 3 3 5 6 7 8 8 8 8
1 2 3 3 5 6 7 8 9 9 11
1 1 1 1 1 1 1 1 1 1 1
1 2 3 3 5 6 7 8 9 10 11
0 1 2 3 4 5 6 7 8 9 10 11
W + 1
Æ
{ 1, 2 }
{ 1, 2, 3 }
{ 1, 2, 3, 4 }
{ 1 }
{ 1, 2, 3, 4, 5 }
n + 1
Subset-sum(n, w1,…, wn, W)
1. for w = 0, 1, …, W do
2. M[0, w] = 0
3. for i = 0, 1, …, n do
4. M[i, 0] = 0
5. for i = 1, 2, .., n do
6. for w = 1, 2, .., W do
7. if (wi > w) then
8. M[i, w] = M[i-1, w]
9. else
10. M[i, w] = max{M[i-1, w], wi +M[i-1, w-wi]}
3 11
11
M
0
0
0
0
0
0 0 0 0 0 0 0 0 0 0 0 0
1 2 3 3 3 3 3 3 3 3 3
1 2 3 3 5 6 7 8 8 8 8
1 2 3 3 5 6 7 8 9 9 11
1 1 1 1 1 1 1 1 1 1 1
1 2 3 3 5 6 7 8 9 10 11
Running time:
O(nW)
IRIS H.-R. JIANG
Pseudo-Polynomial Running Time
¨ Running time: O(nW)
¤ W is not polynomial in input size
¤ “Pseudo-polynomial”
¤ In fact, the subset sum is a computationally hard problem!
n r.f. Karp's 21 NP-complete problems:
n R. M. Karp, "Reducibility among combinatorial problems".
Complexity of Computer Computations. pp. 85--103.
Dynamic programming
35
IRIS H.-R. JIANG
The Knapsack Problem
¨ Given
¤ A set of n items and a knapsack
¤ Item i weighs wi > 0 and has value vi > 0.
¤ The knapsack has capacity of W.
¨ Goal:
¤ Fill the knapsack so as to maximize total value.
n Maximize SiÎS vi
¨ Optimization problem formulation
¤ max SiÎS vi
s.t. SiÎS wi < W, SÍ{1, …, n}
¨ Greedy ¹ optimal
¤ Largest vi first: 28+6+1 = 35
¤ Optimal: 18+22 = 40
Dynamic programming
36
ue.
Karp's 21 NP-complete problems:
R. M. Karp, "Reducibility among combinatorial problems".
Complexity of Computer Computations. pp. 85–103.
1
Value
18
22
28
1
Weight
5
6
6 2
7
Item
1
3
4
5
2
W = 11](https://image.slidesharecdn.com/algorithm6dynamicprogramming-220522073057-711c84d9/85/algorithm_6dynamic_programming-pdf-33-320.jpg)
![IRIS H.-R. JIANG
DP: Iteration
Dynamic programming
33
OPT(i, w) = 0 if i, w = 0
OPT(i-1, w) if wi > w
max {OPT(i-1, w), wi + OPT(i-1, w-wi)} otherwise
Subset-sum(n, w1,…, wn, W)
1. for w = 0, 1, …, W do
2. M[0, w] = 0
3. for i = 0, 1, …, n do
4. M[i, 0] = 0
5. for i = 1, 2, .., n do
6. for w = 1, 2, .., W do
7. if (wi > w) then
8. M[i, w] = M[i-1, w]
9. else
10. M[i, w] = max {M[i-1, w], wi +M[i-1, w-wi]}
IRIS H.-R. JIANG
Example
Dynamic programming
34
1
Weight
5
6
2
7
Item
1
3
4
5
2
W = 11
0
0
0
0
0
0 0 0 0 0 0 0 0 0 0 0 0
1 2 3 3 3 3 3 3 3 3 3
1 2 3 3 5 6 7 8 8 8 8
1 2 3 3 5 6 7 8 9 9 11
1 1 1 1 1 1 1 1 1 1 1
1 2 3 3 5 6 7 8 9 10 11
0 1 2 3 4 5 6 7 8 9 10 11
W + 1
Æ
{ 1, 2 }
{ 1, 2, 3 }
{ 1, 2, 3, 4 }
{ 1 }
{ 1, 2, 3, 4, 5 }
n + 1
Subset-sum(n, w1,…, wn, W)
1. for w = 0, 1, …, W do
2. M[0, w] = 0
3. for i = 0, 1, …, n do
4. M[i, 0] = 0
5. for i = 1, 2, .., n do
6. for w = 1, 2, .., W do
7. if (wi > w) then
8. M[i, w] = M[i-1, w]
9. else
10. M[i, w] = max{M[i-1, w], wi +M[i-1, w-wi]}
3 11
11
M
0
0
0
0
0
0 0 0 0 0 0 0 0 0 0 0 0
1 2 3 3 3 3 3 3 3 3 3
1 2 3 3 5 6 7 8 8 8 8
1 2 3 3 5 6 7 8 9 9 11
1 1 1 1 1 1 1 1 1 1 1
1 2 3 3 5 6 7 8 9 10 11
Running time:
O(nW)
IRIS H.-R. JIANG
Pseudo-Polynomial Running Time
¨ Running time: O(nW)
¤ W is not polynomial in input size
¤ “Pseudo-polynomial”
¤ In fact, the subset sum is a computationally hard problem!
n r.f. Karp's 21 NP-complete problems:
n R. M. Karp, "Reducibility among combinatorial problems".
Complexity of Computer Computations. pp. 85--103.
Dynamic programming
35
IRIS H.-R. JIANG
The Knapsack Problem
¨ Given
¤ A set of n items and a knapsack
¤ Item i weighs wi > 0 and has value vi > 0.
¤ The knapsack has capacity of W.
¨ Goal:
¤ Fill the knapsack so as to maximize total value.
n Maximize SiÎS vi
¨ Optimization problem formulation
¤ max SiÎS vi
s.t. SiÎS wi < W, SÍ{1, …, n}
¨ Greedy ¹ optimal
¤ Largest vi first: 28+6+1 = 35
¤ Optimal: 18+22 = 40
Dynamic programming
36
ue.
Karp's 21 NP-complete problems:
R. M. Karp, "Reducibility among combinatorial problems".
Complexity of Computer Computations. pp. 85–103.
1
Value
18
22
28
1
Weight
5
6
6 2
7
Item
1
3
4
5
2
W = 11](https://image.slidesharecdn.com/algorithm6dynamicprogramming-220522073057-711c84d9/85/algorithm_6dynamic_programming-pdf-34-320.jpg)
![IRIS H.-R. JIANG
DP: Iteration
Dynamic programming
33
OPT(i, w) = 0 if i, w = 0
OPT(i-1, w) if wi > w
max {OPT(i-1, w), wi + OPT(i-1, w-wi)} otherwise
Subset-sum(n, w1,…, wn, W)
1. for w = 0, 1, …, W do
2. M[0, w] = 0
3. for i = 0, 1, …, n do
4. M[i, 0] = 0
5. for i = 1, 2, .., n do
6. for w = 1, 2, .., W do
7. if (wi > w) then
8. M[i, w] = M[i-1, w]
9. else
10. M[i, w] = max {M[i-1, w], wi +M[i-1, w-wi]}
IRIS H.-R. JIANG
Example
Dynamic programming
34
1
Weight
5
6
2
7
Item
1
3
4
5
2
W = 11
0
0
0
0
0
0 0 0 0 0 0 0 0 0 0 0 0
1 2 3 3 3 3 3 3 3 3 3
1 2 3 3 5 6 7 8 8 8 8
1 2 3 3 5 6 7 8 9 9 11
1 1 1 1 1 1 1 1 1 1 1
1 2 3 3 5 6 7 8 9 10 11
0 1 2 3 4 5 6 7 8 9 10 11
W + 1
Æ
{ 1, 2 }
{ 1, 2, 3 }
{ 1, 2, 3, 4 }
{ 1 }
{ 1, 2, 3, 4, 5 }
n + 1
Subset-sum(n, w1,…, wn, W)
1. for w = 0, 1, …, W do
2. M[0, w] = 0
3. for i = 0, 1, …, n do
4. M[i, 0] = 0
5. for i = 1, 2, .., n do
6. for w = 1, 2, .., W do
7. if (wi > w) then
8. M[i, w] = M[i-1, w]
9. else
10. M[i, w] = max{M[i-1, w], wi +M[i-1, w-wi]}
3 11
11
M
0
0
0
0
0
0 0 0 0 0 0 0 0 0 0 0 0
1 2 3 3 3 3 3 3 3 3 3
1 2 3 3 5 6 7 8 8 8 8
1 2 3 3 5 6 7 8 9 9 11
1 1 1 1 1 1 1 1 1 1 1
1 2 3 3 5 6 7 8 9 10 11
Running time:
O(nW)
IRIS H.-R. JIANG
Pseudo-Polynomial Running Time
¨ Running time: O(nW)
¤ W is not polynomial in input size
¤ “Pseudo-polynomial”
¤ In fact, the subset sum is a computationally hard problem!
n r.f. Karp's 21 NP-complete problems:
n R. M. Karp, "Reducibility among combinatorial problems".
Complexity of Computer Computations. pp. 85--103.
Dynamic programming
35
IRIS H.-R. JIANG
The Knapsack Problem
¨ Given
¤ A set of n items and a knapsack
¤ Item i weighs wi > 0 and has value vi > 0.
¤ The knapsack has capacity of W.
¨ Goal:
¤ Fill the knapsack so as to maximize total value.
n Maximize SiÎS vi
¨ Optimization problem formulation
¤ max SiÎS vi
s.t. SiÎS wi < W, SÍ{1, …, n}
¨ Greedy ¹ optimal
¤ Largest vi first: 28+6+1 = 35
¤ Optimal: 18+22 = 40
Dynamic programming
36
ue.
Karp's 21 NP-complete problems:
R. M. Karp, "Reducibility among combinatorial problems".
Complexity of Computer Computations. pp. 85–103.
1
Value
18
22
28
1
Weight
5
6
6 2
7
Item
1
3
4
5
2
W = 11](https://image.slidesharecdn.com/algorithm6dynamicprogramming-220522073057-711c84d9/85/algorithm_6dynamic_programming-pdf-35-320.jpg)
![IRIS H.-R. JIANG
DP: Iteration
Dynamic programming
33
OPT(i, w) = 0 if i, w = 0
OPT(i-1, w) if wi > w
max {OPT(i-1, w), wi + OPT(i-1, w-wi)} otherwise
Subset-sum(n, w1,…, wn, W)
1. for w = 0, 1, …, W do
2. M[0, w] = 0
3. for i = 0, 1, …, n do
4. M[i, 0] = 0
5. for i = 1, 2, .., n do
6. for w = 1, 2, .., W do
7. if (wi > w) then
8. M[i, w] = M[i-1, w]
9. else
10. M[i, w] = max {M[i-1, w], wi +M[i-1, w-wi]}
IRIS H.-R. JIANG
Example
Dynamic programming
34
1
Weight
5
6
2
7
Item
1
3
4
5
2
W = 11
0
0
0
0
0
0 0 0 0 0 0 0 0 0 0 0 0
1 2 3 3 3 3 3 3 3 3 3
1 2 3 3 5 6 7 8 8 8 8
1 2 3 3 5 6 7 8 9 9 11
1 1 1 1 1 1 1 1 1 1 1
1 2 3 3 5 6 7 8 9 10 11
0 1 2 3 4 5 6 7 8 9 10 11
W + 1
Æ
{ 1, 2 }
{ 1, 2, 3 }
{ 1, 2, 3, 4 }
{ 1 }
{ 1, 2, 3, 4, 5 }
n + 1
Subset-sum(n, w1,…, wn, W)
1. for w = 0, 1, …, W do
2. M[0, w] = 0
3. for i = 0, 1, …, n do
4. M[i, 0] = 0
5. for i = 1, 2, .., n do
6. for w = 1, 2, .., W do
7. if (wi > w) then
8. M[i, w] = M[i-1, w]
9. else
10. M[i, w] = max{M[i-1, w], wi +M[i-1, w-wi]}
3 11
11
M
0
0
0
0
0
0 0 0 0 0 0 0 0 0 0 0 0
1 2 3 3 3 3 3 3 3 3 3
1 2 3 3 5 6 7 8 8 8 8
1 2 3 3 5 6 7 8 9 9 11
1 1 1 1 1 1 1 1 1 1 1
1 2 3 3 5 6 7 8 9 10 11
Running time:
O(nW)
IRIS H.-R. JIANG
Pseudo-Polynomial Running Time
¨ Running time: O(nW)
¤ W is not polynomial in input size
¤ “Pseudo-polynomial”
¤ In fact, the subset sum is a computationally hard problem!
n r.f. Karp's 21 NP-complete problems:
n R. M. Karp, "Reducibility among combinatorial problems".
Complexity of Computer Computations. pp. 85--103.
Dynamic programming
35
IRIS H.-R. JIANG
The Knapsack Problem
¨ Given
¤ A set of n items and a knapsack
¤ Item i weighs wi > 0 and has value vi > 0.
¤ The knapsack has capacity of W.
¨ Goal:
¤ Fill the knapsack so as to maximize total value.
n Maximize SiÎS vi
¨ Optimization problem formulation
¤ max SiÎS vi
s.t. SiÎS wi < W, SÍ{1, …, n}
¨ Greedy ¹ optimal
¤ Largest vi first: 28+6+1 = 35
¤ Optimal: 18+22 = 40
Dynamic programming
36
ue.
Karp's 21 NP-complete problems:
R. M. Karp, "Reducibility among combinatorial problems".
Complexity of Computer Computations. pp. 85–103.
1
Value
18
22
28
1
Weight
5
6
6 2
7
Item
1
3
4
5
2
W = 11](https://image.slidesharecdn.com/algorithm6dynamicprogramming-220522073057-711c84d9/85/algorithm_6dynamic_programming-pdf-36-320.jpg)




![IRIS H.-R. JIANG
Bellman-Ford Algorithm (1/2)
¨ Induction either on nodes or on edges works!
¨ If G has no negative cycles, then there is a shortest path from s
to t that is simple (i.e., does not repeat nodes), and hence has
at most n-1 edges.
¨ Pf:
¤ Suppose the shortest path P from s to t repeat a node v.
¤ Since every cycle has nonnegative cost, we could remove the
portion of P between consecutive visits to v resulting in a simple
path Q of no greater cost and fewer edges.
n c(Q) = c(P) – c(C) £ c(P)
Dynamic programming
41
v
s t
C c(C) ³ 0
IRIS H.-R. JIANG
Bellman-Ford Algorithm (2/2)
¨ Induction on edges
¨ OPT(i, v) = length of shortest v-t path P using at most i edges.
¤ OPT(n-1, s) = length of shortest s-t path.
¤ Case 1: P uses at most i-1 edges.
n OPT(i, v) = OPT(i-1, v)
¤ Case 2: P uses exactly i edges.
n OPT(i, v) = cvw + OPT(i-1, w)
n If (v, w) is the first edge, then P uses (v, w) and then selects
the shortest w-t path using at most i-1 edges
Dynamic programming
42
v t
at most i-1 edges
:
:
w
OPT(i, v) = 0 if i = 0, v = t
¥ if i = 0, v ¹ t
min{OPT(i-1, v), min(v, w)ÎE {cvw + OPT(i-1, w)}} otherwise
t
at most i-1 edges
v
IRIS H.-R. JIANG
Implementation: Iteration
Dynamic programming
43
Bellman-Ford(G, s, t)
// n = # of nodes in G
// M[0.. n-1, V]: table recording optimal solutions of subproblems
1. M[0, t] = 0
2. foreach vÎV-{t} do
3. M[0, v] = ¥
4. for i = 1 to n-1 do
5. for vÎV in any order do
6. M[i, v]=min{M[i-1, v], min(v, w)ÎE {cvw + M[i-1, w]}}
OPT(i, v) = 0 if i = 0, v = t
¥ if i = 0, v ¹ t
min{OPT(i-1, v), min(v, w)ÎE {cvw + OPT(i-1, w)}} otherwise
IRIS H.-R. JIANG
M
Example
Dynamic programming
44
Bellman-Ford(G, s, t)
// n = # of nodes in G
// M[0.. n-1, V]: table recording optimal solutions of subproblems
1. M[0, t] = 0
2. foreach vÎV-{t} do
3. M[0, v] = ¥
4. for i = 1 to n-1 do
5. for vÎV in any order do
6. M[i, v]=min{M[i-1, v], min(v, w)ÎE {cvw + M[i-1, w]}}
¥
¥
¥
¥
¥
0
¥
3
4
-3
2
0
0
3
3
-3
0
0
-2
3
3
-4
0
0
-2
3
2
-6
0
0
-2
3
0
-6
0
0 1 2 3 4 5
n
t
b
c
d
a
e
n
0
Space: O(n2)
Running time:
1. naïve:
O(n3)
2. detailed:
O(nm)
b
d
t
e
-1
-2
4
2
c
-3
8
a
-4
6 -3
3
¥
¥
¥
¥
¥
0
¥
3
4
-3
2
0
0
3
3
-3
0
0
-2
3
3
-4
0
0
-2
3
2
-6
0
0
-2
3
0
-6
0
0
b t
e
c
a
Q: How to find the shortest path?
A: Record “successor” for each entry
M[d, 2] =min{M[d,1],
cda+M[a,1]}](https://image.slidesharecdn.com/algorithm6dynamicprogramming-220522073057-711c84d9/85/algorithm_6dynamic_programming-pdf-41-320.jpg)
![IRIS H.-R. JIANG
Bellman-Ford Algorithm (1/2)
¨ Induction either on nodes or on edges works!
¨ If G has no negative cycles, then there is a shortest path from s
to t that is simple (i.e., does not repeat nodes), and hence has
at most n-1 edges.
¨ Pf:
¤ Suppose the shortest path P from s to t repeat a node v.
¤ Since every cycle has nonnegative cost, we could remove the
portion of P between consecutive visits to v resulting in a simple
path Q of no greater cost and fewer edges.
n c(Q) = c(P) – c(C) £ c(P)
Dynamic programming
41
v
s t
C c(C) ³ 0
IRIS H.-R. JIANG
Bellman-Ford Algorithm (2/2)
¨ Induction on edges
¨ OPT(i, v) = length of shortest v-t path P using at most i edges.
¤ OPT(n-1, s) = length of shortest s-t path.
¤ Case 1: P uses at most i-1 edges.
n OPT(i, v) = OPT(i-1, v)
¤ Case 2: P uses exactly i edges.
n OPT(i, v) = cvw + OPT(i-1, w)
n If (v, w) is the first edge, then P uses (v, w) and then selects
the shortest w-t path using at most i-1 edges
Dynamic programming
42
v t
at most i-1 edges
:
:
w
OPT(i, v) = 0 if i = 0, v = t
¥ if i = 0, v ¹ t
min{OPT(i-1, v), min(v, w)ÎE {cvw + OPT(i-1, w)}} otherwise
t
at most i-1 edges
v
IRIS H.-R. JIANG
Implementation: Iteration
Dynamic programming
43
Bellman-Ford(G, s, t)
// n = # of nodes in G
// M[0.. n-1, V]: table recording optimal solutions of subproblems
1. M[0, t] = 0
2. foreach vÎV-{t} do
3. M[0, v] = ¥
4. for i = 1 to n-1 do
5. for vÎV in any order do
6. M[i, v]=min{M[i-1, v], min(v, w)ÎE {cvw + M[i-1, w]}}
OPT(i, v) = 0 if i = 0, v = t
¥ if i = 0, v ¹ t
min{OPT(i-1, v), min(v, w)ÎE {cvw + OPT(i-1, w)}} otherwise
IRIS H.-R. JIANG
M
Example
Dynamic programming
44
Bellman-Ford(G, s, t)
// n = # of nodes in G
// M[0.. n-1, V]: table recording optimal solutions of subproblems
1. M[0, t] = 0
2. foreach vÎV-{t} do
3. M[0, v] = ¥
4. for i = 1 to n-1 do
5. for vÎV in any order do
6. M[i, v]=min{M[i-1, v], min(v, w)ÎE {cvw + M[i-1, w]}}
¥
¥
¥
¥
¥
0
¥
3
4
-3
2
0
0
3
3
-3
0
0
-2
3
3
-4
0
0
-2
3
2
-6
0
0
-2
3
0
-6
0
0 1 2 3 4 5
n
t
b
c
d
a
e
n
0
Space: O(n2)
Running time:
1. naïve:
O(n3)
2. detailed:
O(nm)
b
d
t
e
-1
-2
4
2
c
-3
8
a
-4
6 -3
3
¥
¥
¥
¥
¥
0
¥
3
4
-3
2
0
0
3
3
-3
0
0
-2
3
3
-4
0
0
-2
3
2
-6
0
0
-2
3
0
-6
0
0
b t
e
c
a
Q: How to find the shortest path?
A: Record “successor” for each entry
M[d, 2] =min{M[d,1],
cda+M[a,1]}](https://image.slidesharecdn.com/algorithm6dynamicprogramming-220522073057-711c84d9/85/algorithm_6dynamic_programming-pdf-42-320.jpg)
![IRIS H.-R. JIANG
Bellman-Ford Algorithm (1/2)
¨ Induction either on nodes or on edges works!
¨ If G has no negative cycles, then there is a shortest path from s
to t that is simple (i.e., does not repeat nodes), and hence has
at most n-1 edges.
¨ Pf:
¤ Suppose the shortest path P from s to t repeat a node v.
¤ Since every cycle has nonnegative cost, we could remove the
portion of P between consecutive visits to v resulting in a simple
path Q of no greater cost and fewer edges.
n c(Q) = c(P) – c(C) £ c(P)
Dynamic programming
41
v
s t
C c(C) ³ 0
IRIS H.-R. JIANG
Bellman-Ford Algorithm (2/2)
¨ Induction on edges
¨ OPT(i, v) = length of shortest v-t path P using at most i edges.
¤ OPT(n-1, s) = length of shortest s-t path.
¤ Case 1: P uses at most i-1 edges.
n OPT(i, v) = OPT(i-1, v)
¤ Case 2: P uses exactly i edges.
n OPT(i, v) = cvw + OPT(i-1, w)
n If (v, w) is the first edge, then P uses (v, w) and then selects
the shortest w-t path using at most i-1 edges
Dynamic programming
42
v t
at most i-1 edges
:
:
w
OPT(i, v) = 0 if i = 0, v = t
¥ if i = 0, v ¹ t
min{OPT(i-1, v), min(v, w)ÎE {cvw + OPT(i-1, w)}} otherwise
t
at most i-1 edges
v
IRIS H.-R. JIANG
Implementation: Iteration
Dynamic programming
43
Bellman-Ford(G, s, t)
// n = # of nodes in G
// M[0.. n-1, V]: table recording optimal solutions of subproblems
1. M[0, t] = 0
2. foreach vÎV-{t} do
3. M[0, v] = ¥
4. for i = 1 to n-1 do
5. for vÎV in any order do
6. M[i, v]=min{M[i-1, v], min(v, w)ÎE {cvw + M[i-1, w]}}
OPT(i, v) = 0 if i = 0, v = t
¥ if i = 0, v ¹ t
min{OPT(i-1, v), min(v, w)ÎE {cvw + OPT(i-1, w)}} otherwise
IRIS H.-R. JIANG
M
Example
Dynamic programming
44
Bellman-Ford(G, s, t)
// n = # of nodes in G
// M[0.. n-1, V]: table recording optimal solutions of subproblems
1. M[0, t] = 0
2. foreach vÎV-{t} do
3. M[0, v] = ¥
4. for i = 1 to n-1 do
5. for vÎV in any order do
6. M[i, v]=min{M[i-1, v], min(v, w)ÎE {cvw + M[i-1, w]}}
¥
¥
¥
¥
¥
0
¥
3
4
-3
2
0
0
3
3
-3
0
0
-2
3
3
-4
0
0
-2
3
2
-6
0
0
-2
3
0
-6
0
0 1 2 3 4 5
n
t
b
c
d
a
e
n
0
Space: O(n2)
Running time:
1. naïve:
O(n3)
2. detailed:
O(nm)
b
d
t
e
-1
-2
4
2
c
-3
8
a
-4
6 -3
3
¥
¥
¥
¥
¥
0
¥
3
4
-3
2
0
0
3
3
-3
0
0
-2
3
3
-4
0
0
-2
3
2
-6
0
0
-2
3
0
-6
0
0
b t
e
c
a
Q: How to find the shortest path?
A: Record “successor” for each entry
M[d, 2] =min{M[d,1],
cda+M[a,1]}](https://image.slidesharecdn.com/algorithm6dynamicprogramming-220522073057-711c84d9/85/algorithm_6dynamic_programming-pdf-43-320.jpg)
![IRIS H.-R. JIANG
Bellman-Ford Algorithm (1/2)
¨ Induction either on nodes or on edges works!
¨ If G has no negative cycles, then there is a shortest path from s
to t that is simple (i.e., does not repeat nodes), and hence has
at most n-1 edges.
¨ Pf:
¤ Suppose the shortest path P from s to t repeat a node v.
¤ Since every cycle has nonnegative cost, we could remove the
portion of P between consecutive visits to v resulting in a simple
path Q of no greater cost and fewer edges.
n c(Q) = c(P) – c(C) £ c(P)
Dynamic programming
41
v
s t
C c(C) ³ 0
IRIS H.-R. JIANG
Bellman-Ford Algorithm (2/2)
¨ Induction on edges
¨ OPT(i, v) = length of shortest v-t path P using at most i edges.
¤ OPT(n-1, s) = length of shortest s-t path.
¤ Case 1: P uses at most i-1 edges.
n OPT(i, v) = OPT(i-1, v)
¤ Case 2: P uses exactly i edges.
n OPT(i, v) = cvw + OPT(i-1, w)
n If (v, w) is the first edge, then P uses (v, w) and then selects
the shortest w-t path using at most i-1 edges
Dynamic programming
42
v t
at most i-1 edges
:
:
w
OPT(i, v) = 0 if i = 0, v = t
¥ if i = 0, v ¹ t
min{OPT(i-1, v), min(v, w)ÎE {cvw + OPT(i-1, w)}} otherwise
t
at most i-1 edges
v
IRIS H.-R. JIANG
Implementation: Iteration
Dynamic programming
43
Bellman-Ford(G, s, t)
// n = # of nodes in G
// M[0.. n-1, V]: table recording optimal solutions of subproblems
1. M[0, t] = 0
2. foreach vÎV-{t} do
3. M[0, v] = ¥
4. for i = 1 to n-1 do
5. for vÎV in any order do
6. M[i, v]=min{M[i-1, v], min(v, w)ÎE {cvw + M[i-1, w]}}
OPT(i, v) = 0 if i = 0, v = t
¥ if i = 0, v ¹ t
min{OPT(i-1, v), min(v, w)ÎE {cvw + OPT(i-1, w)}} otherwise
IRIS H.-R. JIANG
M
Example
Dynamic programming
44
Bellman-Ford(G, s, t)
// n = # of nodes in G
// M[0.. n-1, V]: table recording optimal solutions of subproblems
1. M[0, t] = 0
2. foreach vÎV-{t} do
3. M[0, v] = ¥
4. for i = 1 to n-1 do
5. for vÎV in any order do
6. M[i, v]=min{M[i-1, v], min(v, w)ÎE {cvw + M[i-1, w]}}
¥
¥
¥
¥
¥
0
¥
3
4
-3
2
0
0
3
3
-3
0
0
-2
3
3
-4
0
0
-2
3
2
-6
0
0
-2
3
0
-6
0
0 1 2 3 4 5
n
t
b
c
d
a
e
n
0
Space: O(n2)
Running time:
1. naïve:
O(n3)
2. detailed:
O(nm)
b
d
t
e
-1
-2
4
2
c
-3
8
a
-4
6 -3
3
¥
¥
¥
¥
¥
0
¥
3
4
-3
2
0
0
3
3
-3
0
0
-2
3
3
-4
0
0
-2
3
2
-6
0
0
-2
3
0
-6
0
0
b t
e
c
a
Q: How to find the shortest path?
A: Record “successor” for each entry
M[d, 2] =min{M[d,1],
cda+M[a,1]}](https://image.slidesharecdn.com/algorithm6dynamicprogramming-220522073057-711c84d9/85/algorithm_6dynamic_programming-pdf-44-320.jpg)
![IRIS H.-R. JIANG
Running Time
¨ Lines 5-6:
¤ Naïve: for each v, check v and others: O(n2)
¤ Detailed: for each v, check v and its neighbors (out-going edges):
åvÎV(degout(v)+1) = O(m)
¨ Lines 4-6:
¤ Naïve: O(n3)
¤ Detailed: O(nm)
Dynamic programming
45
0 1 2 3 4 5
n
t
b
c
d
a
e
n
¥
¥
¥
¥
¥
0
¥
3
4
-3
2
0
0
3
3
-3
0
0
-2
3
3
-4
0
0
-2
3
2
-6
0
0
-2
3
0
-6
0
0
b
d
t
e
-1
-2
4
2
c
-3
8
a
-4
6 -3
3
Bellman-Ford(G, s, t)
:
4. for i = 1 to n-1 do
5. for vÎV in any order do
6. M[i, v]=min{M[i-1, v], min(v, w)ÎE {cvw + M[i-1, w]}}
IRIS H.-R. JIANG
Space Improvement
¨ Maintain a 1D array instead:
¤ M[v] = shortest v-t path length that we have found so far.
¤ Iterator i is simply a counter
¤ No need to check edges of the form (v, w) unless M[w] changed
in previous iteration.
¤ In each iteration, for each node v,
M[v]=min{M[v], minwÎV {cvw + M[w]}}
¨ Observation: Throughout the algorithm, M[v] is the length of some
v-t path, and after i rounds of updates, the value M[v] is no larger
than the length of shortest v-t path using at most i edges.
Dynamic programming
46
Computing Science is –and will always be– concerned with the interplay
between mechanized and human symbol manipulation, which usually referred
to as “computing” and “programming” respectively.
~ E. W. Dijkstra
IRIS H.-R. JIANG
Negative Cycles?
¨ If a s-t path in a general graph G passes through node v, and v
belongs to a negative cycle C, Bellman-Ford algorithm fails to
find the shortest s-t path.
¤ Reduce cost over and over again using the negative cycle
Dynamic programming
47
v
s t
C c(C) < 0
IRIS H.-R. JIANG
Application: Currency Conversion (1/2)
¨ Q: Given n currencies and exchange rates between pairs of
currencies, is there an arbitrage opportunity?
¤ The currency graph:
n Node: currency; edge cost: exchange rate ruv: ruv*rvu <1
¤ Arbitrage: a cycle on which product of edge costs >1
n E.g., $1 Þ 1.3941 Francs Þ 0.9308 Euros Þ $1.00084
Dynamic programming
48
Courtesy of Prof. Kevin Wayne @ Princeton
G
£ F E
¥
$
0.003065
455.2
208.1
0.004816
2.1904
1.3941
0.6677
327.25
129.52
0.008309
1.0752
$
1.3941
F 0.6677 E
1.0752](https://image.slidesharecdn.com/algorithm6dynamicprogramming-220522073057-711c84d9/85/algorithm_6dynamic_programming-pdf-45-320.jpg)
![IRIS H.-R. JIANG
Running Time
¨ Lines 5-6:
¤ Naïve: for each v, check v and others: O(n2)
¤ Detailed: for each v, check v and its neighbors (out-going edges):
åvÎV(degout(v)+1) = O(m)
¨ Lines 4-6:
¤ Naïve: O(n3)
¤ Detailed: O(nm)
Dynamic programming
45
0 1 2 3 4 5
n
t
b
c
d
a
e
n
¥
¥
¥
¥
¥
0
¥
3
4
-3
2
0
0
3
3
-3
0
0
-2
3
3
-4
0
0
-2
3
2
-6
0
0
-2
3
0
-6
0
0
b
d
t
e
-1
-2
4
2
c
-3
8
a
-4
6 -3
3
Bellman-Ford(G, s, t)
:
4. for i = 1 to n-1 do
5. for vÎV in any order do
6. M[i, v]=min{M[i-1, v], min(v, w)ÎE {cvw + M[i-1, w]}}
IRIS H.-R. JIANG
Space Improvement
¨ Maintain a 1D array instead:
¤ M[v] = shortest v-t path length that we have found so far.
¤ Iterator i is simply a counter
¤ No need to check edges of the form (v, w) unless M[w] changed
in previous iteration.
¤ In each iteration, for each node v,
M[v]=min{M[v], minwÎV {cvw + M[w]}}
¨ Observation: Throughout the algorithm, M[v] is the length of some
v-t path, and after i rounds of updates, the value M[v] is no larger
than the length of shortest v-t path using at most i edges.
Dynamic programming
46
Computing Science is –and will always be– concerned with the interplay
between mechanized and human symbol manipulation, which usually referred
to as “computing” and “programming” respectively.
~ E. W. Dijkstra
IRIS H.-R. JIANG
Negative Cycles?
¨ If a s-t path in a general graph G passes through node v, and v
belongs to a negative cycle C, Bellman-Ford algorithm fails to
find the shortest s-t path.
¤ Reduce cost over and over again using the negative cycle
Dynamic programming
47
v
s t
C c(C) < 0
IRIS H.-R. JIANG
Application: Currency Conversion (1/2)
¨ Q: Given n currencies and exchange rates between pairs of
currencies, is there an arbitrage opportunity?
¤ The currency graph:
n Node: currency; edge cost: exchange rate ruv: ruv*rvu <1
¤ Arbitrage: a cycle on which product of edge costs >1
n E.g., $1 Þ 1.3941 Francs Þ 0.9308 Euros Þ $1.00084
Dynamic programming
48
Courtesy of Prof. Kevin Wayne @ Princeton
G
£ F E
¥
$
0.003065
455.2
208.1
0.004816
2.1904
1.3941
0.6677
327.25
129.52
0.008309
1.0752
$
1.3941
F 0.6677 E
1.0752](https://image.slidesharecdn.com/algorithm6dynamicprogramming-220522073057-711c84d9/85/algorithm_6dynamic_programming-pdf-46-320.jpg)
![IRIS H.-R. JIANG
Running Time
¨ Lines 5-6:
¤ Naïve: for each v, check v and others: O(n2)
¤ Detailed: for each v, check v and its neighbors (out-going edges):
åvÎV(degout(v)+1) = O(m)
¨ Lines 4-6:
¤ Naïve: O(n3)
¤ Detailed: O(nm)
Dynamic programming
45
0 1 2 3 4 5
n
t
b
c
d
a
e
n
¥
¥
¥
¥
¥
0
¥
3
4
-3
2
0
0
3
3
-3
0
0
-2
3
3
-4
0
0
-2
3
2
-6
0
0
-2
3
0
-6
0
0
b
d
t
e
-1
-2
4
2
c
-3
8
a
-4
6 -3
3
Bellman-Ford(G, s, t)
:
4. for i = 1 to n-1 do
5. for vÎV in any order do
6. M[i, v]=min{M[i-1, v], min(v, w)ÎE {cvw + M[i-1, w]}}
IRIS H.-R. JIANG
Space Improvement
¨ Maintain a 1D array instead:
¤ M[v] = shortest v-t path length that we have found so far.
¤ Iterator i is simply a counter
¤ No need to check edges of the form (v, w) unless M[w] changed
in previous iteration.
¤ In each iteration, for each node v,
M[v]=min{M[v], minwÎV {cvw + M[w]}}
¨ Observation: Throughout the algorithm, M[v] is the length of some
v-t path, and after i rounds of updates, the value M[v] is no larger
than the length of shortest v-t path using at most i edges.
Dynamic programming
46
Computing Science is –and will always be– concerned with the interplay
between mechanized and human symbol manipulation, which usually referred
to as “computing” and “programming” respectively.
~ E. W. Dijkstra
IRIS H.-R. JIANG
Negative Cycles?
¨ If a s-t path in a general graph G passes through node v, and v
belongs to a negative cycle C, Bellman-Ford algorithm fails to
find the shortest s-t path.
¤ Reduce cost over and over again using the negative cycle
Dynamic programming
47
v
s t
C c(C) < 0
IRIS H.-R. JIANG
Application: Currency Conversion (1/2)
¨ Q: Given n currencies and exchange rates between pairs of
currencies, is there an arbitrage opportunity?
¤ The currency graph:
n Node: currency; edge cost: exchange rate ruv: ruv*rvu <1
¤ Arbitrage: a cycle on which product of edge costs >1
n E.g., $1 Þ 1.3941 Francs Þ 0.9308 Euros Þ $1.00084
Dynamic programming
48
Courtesy of Prof. Kevin Wayne @ Princeton
G
£ F E
¥
$
0.003065
455.2
208.1
0.004816
2.1904
1.3941
0.6677
327.25
129.52
0.008309
1.0752
$
1.3941
F 0.6677 E
1.0752](https://image.slidesharecdn.com/algorithm6dynamicprogramming-220522073057-711c84d9/85/algorithm_6dynamic_programming-pdf-47-320.jpg)
![IRIS H.-R. JIANG
Running Time
¨ Lines 5-6:
¤ Naïve: for each v, check v and others: O(n2)
¤ Detailed: for each v, check v and its neighbors (out-going edges):
åvÎV(degout(v)+1) = O(m)
¨ Lines 4-6:
¤ Naïve: O(n3)
¤ Detailed: O(nm)
Dynamic programming
45
0 1 2 3 4 5
n
t
b
c
d
a
e
n
¥
¥
¥
¥
¥
0
¥
3
4
-3
2
0
0
3
3
-3
0
0
-2
3
3
-4
0
0
-2
3
2
-6
0
0
-2
3
0
-6
0
0
b
d
t
e
-1
-2
4
2
c
-3
8
a
-4
6 -3
3
Bellman-Ford(G, s, t)
:
4. for i = 1 to n-1 do
5. for vÎV in any order do
6. M[i, v]=min{M[i-1, v], min(v, w)ÎE {cvw + M[i-1, w]}}
IRIS H.-R. JIANG
Space Improvement
¨ Maintain a 1D array instead:
¤ M[v] = shortest v-t path length that we have found so far.
¤ Iterator i is simply a counter
¤ No need to check edges of the form (v, w) unless M[w] changed
in previous iteration.
¤ In each iteration, for each node v,
M[v]=min{M[v], minwÎV {cvw + M[w]}}
¨ Observation: Throughout the algorithm, M[v] is the length of some
v-t path, and after i rounds of updates, the value M[v] is no larger
than the length of shortest v-t path using at most i edges.
Dynamic programming
46
Computing Science is –and will always be– concerned with the interplay
between mechanized and human symbol manipulation, which usually referred
to as “computing” and “programming” respectively.
~ E. W. Dijkstra
IRIS H.-R. JIANG
Negative Cycles?
¨ If a s-t path in a general graph G passes through node v, and v
belongs to a negative cycle C, Bellman-Ford algorithm fails to
find the shortest s-t path.
¤ Reduce cost over and over again using the negative cycle
Dynamic programming
47
v
s t
C c(C) < 0
IRIS H.-R. JIANG
Application: Currency Conversion (1/2)
¨ Q: Given n currencies and exchange rates between pairs of
currencies, is there an arbitrage opportunity?
¤ The currency graph:
n Node: currency; edge cost: exchange rate ruv: ruv*rvu <1
¤ Arbitrage: a cycle on which product of edge costs >1
n E.g., $1 Þ 1.3941 Francs Þ 0.9308 Euros Þ $1.00084
Dynamic programming
48
Courtesy of Prof. Kevin Wayne @ Princeton
G
£ F E
¥
$
0.003065
455.2
208.1
0.004816
2.1904
1.3941
0.6677
327.25
129.52
0.008309
1.0752
$
1.3941
F 0.6677 E
1.0752](https://image.slidesharecdn.com/algorithm6dynamicprogramming-220522073057-711c84d9/85/algorithm_6dynamic_programming-pdf-48-320.jpg)







