Algorithms Lecture 3: Analysis of Algorithms II
4 likes2,034 views
The document discusses the analysis and design of algorithms, focusing on the maximum pairwise product, Fibonacci sequence, and greatest common divisors (GCD). It presents naive and efficient algorithms for calculating these values, emphasizing the importance of time complexity. Efficient algorithms reduce computational steps, highlighting the differences in performance between naive and advanced approaches.
1 of 65
Downloaded 157 times









![Analysis and Design of Algorithms
Assume the following array
2 4 3 5 1
i j
If a[i]*a[j] > result
result=a[i]*a[j]=8](https://image.slidesharecdn.com/algorithms-lecture3-171010195222/85/Algorithms-Lecture-3-Analysis-of-Algorithms-II-10-320.jpg)
![Analysis and Design of Algorithms
Assume the following array
2 4 3 5 1
i j
If a[i]*a[j] > result
result=8](https://image.slidesharecdn.com/algorithms-lecture3-171010195222/85/Algorithms-Lecture-3-Analysis-of-Algorithms-II-11-320.jpg)
![Analysis and Design of Algorithms
Assume the following array
2 4 3 5 1
i j
If a[i]*a[j] > result
result= a[i]*a[j] =10](https://image.slidesharecdn.com/algorithms-lecture3-171010195222/85/Algorithms-Lecture-3-Analysis-of-Algorithms-II-12-320.jpg)




















































Ad
Recommended
Algorithms Lecture 2: Analysis of Algorithms I
Algorithms Lecture 2: Analysis of Algorithms IMohamed Loey This document discusses analysis of algorithms and time complexity. It explains that analysis of algorithms determines the resources needed to execute algorithms. The time complexity of an algorithm quantifies how long it takes. There are three cases to analyze - worst case, average case, and best case. Common notations for time complexity include O(1), O(n), O(n^2), O(log n), and O(n!). The document provides examples of algorithms and determines their time complexity in different cases. It also discusses how to combine complexities of nested loops and loops in algorithms.
Algorithms Lecture 5: Sorting Algorithms II
Algorithms Lecture 5: Sorting Algorithms IIMohamed Loey The document discusses sorting algorithms, focusing primarily on counting sort, which is a non-comparison based sorting technique that counts the occurrences of each unique key within a defined range. It outlines the steps for implementing counting sort, including creating a count array, modifying it, and producing the output array based on this count. An illustrative example is provided to demonstrate the counting sort process and its implementation details.
Algorithms Lecture 6: Searching Algorithms
Algorithms Lecture 6: Searching AlgorithmsMohamed Loey The document discusses various searching algorithms, including linear search, binary search, jump search, and interpolation search. Each algorithm is detailed with its methodology, examples, and time complexities, highlighting their efficiencies in different scenarios. Overall, it serves as a guide to understanding and implementing these algorithms in programming.
Algorithms Lecture 4: Sorting Algorithms I
Algorithms Lecture 4: Sorting Algorithms IMohamed Loey The document discusses three sorting algorithms: bubble sort, selection sort, and insertion sort. Bubble sort works by repeatedly swapping adjacent elements that are in the wrong order. Selection sort finds the minimum element and swaps it into the sorted portion of the array. Insertion sort inserts elements into the sorted portion of the array, swapping as needed to put the element in the correct position. Both selection sort and insertion sort have a time complexity of O(n^2) in the worst case.
Algorithms Lecture 1: Introduction to Algorithms
Algorithms Lecture 1: Introduction to AlgorithmsMohamed Loey The document discusses the analysis and design of algorithms, focusing on time and space complexity while distinguishing between various algorithm types and their applications. It highlights the use of Python as a preferred programming language due to its ease of use, supportive community, and extensive libraries like NumPy and SciPy. The document also covers pseudocode as an informal method of describing algorithms and provides examples of sorting and searching algorithms.
Algorithms Lecture 7: Graph Algorithms
Algorithms Lecture 7: Graph AlgorithmsMohamed Loey The document provides a comprehensive analysis and design of algorithms related to graph theory, focusing on concepts such as directed and undirected graphs, acyclic and cyclic graphs, and techniques for graph traversal including breadth-first and depth-first search methods. It explains the significance of vertices and edges, the operations of searching and traversing nodes, and includes examples illustrating the application of these concepts. Additionally, it addresses cycle detection in directed graphs using depth-first traversal.
Presentation on Elementary data structures
Presentation on Elementary data structuresKuber Chandra The document discusses elementary data structures such as arrays, lists, stacks, and queues, explaining their definitions, characteristics, and operations. It covers complexity analysis of algorithms, including time and space complexity, as well as providing examples of code implementations for stack and queue operations. Additionally, it describes various applications of stacks, including the Tower of Hanoi problem, and details types of queues like circular queues and double-ended queues.
Dynamic programming
Dynamic programmingYıldırım Tam A. Plannig
The document mentions that in dynamic programming, "Programming" refers to "planning", not computer programming.
chapter 1
chapter 1yatheesha This document provides an overview of a lecture on designing and analyzing computer algorithms. It discusses key concepts like what an algorithm and program are, common algorithm design techniques like divide-and-conquer and greedy methods, and how to analyze algorithms' time and space complexity. The goals of analyzing algorithms are to understand their behavior, improve efficiency, and determine whether problems can be solved within a reasonable time frame.
Analysis of algorithm
Analysis of algorithmRajendra Dangwal The document discusses algorithms as step-by-step procedures for problem-solving, emphasizing the importance of analyzing algorithms to determine the best solution based on their execution time relative to input size. It covers the order of growth and examines best, worst, and average case efficiencies for searching elements in a list. Additionally, it introduces big O, big Omega, and big Theta notations for categorizing the performance of algorithms depending on their execution time.
Lecture 2 data structures and algorithms
Lecture 2 data structures and algorithmsAakash deep Singhal The document discusses algorithms and their complexity. It defines an algorithm as a well-defined computational procedure that takes inputs and produces outputs. Algorithms have properties like definiteness, correctness, finiteness, and effectiveness. While faster computers make any method viable, analyzing algorithms' complexity is still important because computing resources are finite. Algorithm complexity is analyzed asymptotically for large inputs, focusing on growth rates like constant, logarithmic, linear, quadratic, and exponential. Common notations like Big-O describe upper algorithm complexity bounds.
Divide and conquer
Divide and conquerDr Shashikant Athawale The document discusses divide and conquer algorithms. It describes divide and conquer as a design strategy that involves dividing a problem into smaller subproblems, solving the subproblems recursively, and combining the solutions. It provides examples of divide and conquer algorithms like merge sort, quicksort, and binary search. Merge sort works by recursively sorting halves of an array until it is fully sorted. Quicksort selects a pivot element and partitions the array into subarrays of smaller and larger elements, recursively sorting the subarrays. Binary search recursively searches half-intervals of a sorted array to find a target value.
Data Structure and Algorithms.pptx
Data Structure and Algorithms.pptxSyed Zaid Irshad The document provides an outline for a course on data structures and algorithms. It includes topics like data types and operations, time-space tradeoffs, algorithm development, asymptotic notations, common data structures, sorting and searching algorithms, and linked lists. The course will use Google Classroom and have assignments, quizzes, and a final exam.
Dinive conquer algorithm
Dinive conquer algorithmMohd Arif The document discusses the divide and conquer algorithm design technique. It begins by explaining the basic approach of divide and conquer which is to (1) divide the problem into subproblems, (2) conquer the subproblems by solving them recursively, and (3) combine the solutions to the subproblems into a solution for the original problem. It then provides merge sort as a specific example of a divide and conquer algorithm for sorting a sequence. It explains that merge sort divides the sequence in half recursively until individual elements remain, then combines the sorted halves back together to produce the fully sorted sequence.
Algorithms Lecture 8: Pattern Algorithms
Algorithms Lecture 8: Pattern AlgorithmsMohamed Loey The document discusses patterns in algorithms, particularly focusing on pattern searching techniques used in computer science. It explains naive pattern searching, provides examples of inputs and outputs, and outlines regular expressions for matching text patterns. Additionally, it covers best and worst-case scenarios for pattern searching and demonstrates the use of Python for regular expressions.
Complexity of Algorithm
Complexity of AlgorithmMuhammad Muzammal This document discusses the complexity of algorithms and the tradeoff between algorithm cost and time. It defines algorithm complexity as a function of input size that measures the time and space used by an algorithm. Different complexity classes are described such as polynomial, sub-linear, and exponential time. Examples are given to find the complexity of bubble sort and linear search algorithms. The concept of space-time tradeoffs is introduced, where using more space can reduce computation time. Genetic algorithms are proposed to efficiently solve large-scale construction time-cost tradeoff problems.
Asymptotic Notation and Complexity
Asymptotic Notation and ComplexityRajandeep Gill The document discusses the analysis of algorithms, focusing on their running time and factors affecting it, such as memory usage and programmer effort. It outlines different types of analysis, including worst case, best case, and average case, as well as asymptotic notation used to compare algorithms. Key concepts include the growth rates of functions and various notations like Big-O, Big-Omega, and Big-Theta to classify algorithm complexity.
Data structures and algorithms
Data structures and algorithmsJulie Iskander The document covers data structures and algorithms, outlining key topics such as sorting (selection sort, bubble sort, merge sort) and searching algorithms (linear search, binary search) alongside their complexities. It describes various data structures, including arrays, linked lists, stacks, queues, and trees, highlighting their characteristics and operations. Additionally, it emphasizes the importance of algorithm analysis, discussing time and space complexities and providing implementation examples in C.
Solving recurrences
Solving recurrencesMegha V The document discusses methods for solving recurrences in algorithms, focusing on recursive and non-recursive algorithms. It presents various techniques such as the iteration method, substitution method, recursion tree method, and the master theorem, illustrated with examples. The content emphasizes finding explicit formulas for recurrences and understanding their running time in relation to algorithmic efficiency.
Algorithm Complexity and Main Concepts
Algorithm Complexity and Main ConceptsAdelina Ahadova An algorithm is a finite set of instructions to accomplish a predefined task. Performance of an algorithm is measured by its time and space complexity, with common metrics being big O, big Omega, and big Theta notation. Common data structures include arrays, linked lists, stacks, queues, trees and graphs. Key concepts are asymptotic analysis of algorithms, recursion, and analyzing complexity classes like constant, linear, quadratic and logarithmic time.
Unit 1 chapter 1 Design and Analysis of Algorithms
Unit 1 chapter 1 Design and Analysis of AlgorithmsP. Subathra Kishore, KAMARAJ College of Engineering and Technology, Madurai The document introduces algorithms, outlining their definition, design, and implementation steps while highlighting important problem types and fundamental data structures. It explains the concept of algorithms through examples like finding the greatest common divisor (gcd) and generating prime numbers. The document also touches on algorithm efficiency, correctness, and various problem-solving techniques.
Design and Analysis of Algorithms
Design and Analysis of AlgorithmsSwapnil Agrawal The document discusses the analysis of algorithms. It begins by defining an algorithm and describing different types. It then covers analyzing algorithms in terms of correctness, time efficiency, space efficiency, and optimality through theoretical and empirical analysis. The document discusses analyzing time efficiency by determining the number of repetitions of basic operations as a function of input size. It provides examples of input size, basic operations, and formulas for counting operations. It also covers analyzing best, worst, and average cases and establishes asymptotic efficiency classes. The document then analyzes several examples of non-recursive and recursive algorithms.
Daa unit 1
Daa unit 1Abhimanyu Mishra The document discusses algorithms and their analysis. It covers:
1) The definition of an algorithm and its key characteristics like being unambiguous, finite, and efficient.
2) The fundamental steps of algorithmic problem solving like understanding the problem, designing a solution, and analyzing efficiency.
3) Methods for specifying algorithms using pseudocode, flowcharts, or natural language.
4) Analyzing an algorithm's time and space efficiency using asymptotic analysis and orders of growth like best-case, worst-case, and average-case scenarios.
Lecture 4 asymptotic notations
Lecture 4 asymptotic notationsjayavignesh86 This document discusses asymptotic notations and their use in analyzing the time complexity of algorithms. It introduces the Big-O, Big-Omega, and Big-Theta notations for describing the asymptotic upper bound, lower bound, and tight bound of an algorithm's running time. The document explains that asymptotic notations allow algorithms to be compared by ignoring lower-order terms and constants, and focusing on the highest-order term that dominates as the input size increases. Examples are provided to illustrate the different orders of growth and the notations used to describe them.
Asymptotic notations
Asymptotic notationsNikhil Sharma The document discusses asymptotic notations that are used to describe the time complexity of algorithms. It introduces big O notation, which describes asymptotic upper bounds, big Omega notation for lower bounds, and big Theta notation for tight bounds. Common time complexities are described such as O(1) for constant time, O(log N) for logarithmic time, and O(N^2) for quadratic time. The notations allow analyzing how efficiently algorithms use resources like time and space as the input size increases.
Binary search
Binary searchAparnaKumari31 Binary search is an algorithm that finds the position of a target value within a sorted array. It works by recursively dividing the array range in half and searching only within the appropriate half. The time complexity is O(log n) in the average and worst cases and O(1) in the best case, making it very efficient for searching sorted data. However, it requires the list to be sorted for it to work.
Graph coloring using backtracking
Graph coloring using backtrackingshashidharPapishetty This document summarizes graph coloring using backtracking. It defines graph coloring as minimizing the number of colors used to color a graph. The chromatic number is the fewest colors needed. Graph coloring is NP-complete. The document outlines a backtracking algorithm that tries assigning colors to vertices, checks if the assignment is valid (no adjacent vertices have the same color), and backtracks if not. It provides pseudocode for the algorithm and lists applications like scheduling, Sudoku, and map coloring.
how to calclute time complexity of algortihm
how to calclute time complexity of algortihmSajid Marwat This document discusses algorithm analysis and complexity. It defines key terms like asymptotic complexity, Big-O notation, and time complexity. It provides examples of analyzing simple algorithms like a sum function to determine their time complexity. Common analyses include looking at loops, nested loops, and sequences of statements. The goal is to classify algorithms according to their complexity, which is important for large inputs and machine-independent. Algorithms are classified based on worst, average, and best case analyses.
Computer Security Lecture 5: Simplified Advanced Encryption Standard
Computer Security Lecture 5: Simplified Advanced Encryption StandardMohamed Loey The document provides an overview of the Simplified Advanced Encryption Standard (S-AES), created for educational purposes to help students understand encryption and decryption processes. It details the methods for key generation, block encryption, and decryption using 16-bit keys and plaintext, along with step-by-step transformations such as nibble substitution, row shifting, and column mixing. S-AES allows students to perform encryption operations manually, enhancing their comprehension of the underlying structure of AES.
Deep Learning - Overview of my work II
Deep Learning - Overview of my work IIMohamed Loey The document covers various aspects of deep learning, including definitions of artificial narrow, general, and super intelligence, and details on machine learning techniques like supervised and unsupervised learning. It discusses the architecture of neural networks such as convolutional neural networks and their application in image recognition, speech recognition, and natural language processing, along with datasets like MNIST and CIFAR-10. Techniques to mitigate overfitting in neural networks, such as dropout and L2 regularization, are also highlighted, along with a summary of a new CNN architecture built for classifying Arabic handwritten characters.
More Related Content
What's hot (20)
chapter 1
chapter 1yatheesha This document provides an overview of a lecture on designing and analyzing computer algorithms. It discusses key concepts like what an algorithm and program are, common algorithm design techniques like divide-and-conquer and greedy methods, and how to analyze algorithms' time and space complexity. The goals of analyzing algorithms are to understand their behavior, improve efficiency, and determine whether problems can be solved within a reasonable time frame.
Analysis of algorithm
Analysis of algorithmRajendra Dangwal The document discusses algorithms as step-by-step procedures for problem-solving, emphasizing the importance of analyzing algorithms to determine the best solution based on their execution time relative to input size. It covers the order of growth and examines best, worst, and average case efficiencies for searching elements in a list. Additionally, it introduces big O, big Omega, and big Theta notations for categorizing the performance of algorithms depending on their execution time.
Lecture 2 data structures and algorithms
Lecture 2 data structures and algorithmsAakash deep Singhal The document discusses algorithms and their complexity. It defines an algorithm as a well-defined computational procedure that takes inputs and produces outputs. Algorithms have properties like definiteness, correctness, finiteness, and effectiveness. While faster computers make any method viable, analyzing algorithms' complexity is still important because computing resources are finite. Algorithm complexity is analyzed asymptotically for large inputs, focusing on growth rates like constant, logarithmic, linear, quadratic, and exponential. Common notations like Big-O describe upper algorithm complexity bounds.
Divide and conquer
Divide and conquerDr Shashikant Athawale The document discusses divide and conquer algorithms. It describes divide and conquer as a design strategy that involves dividing a problem into smaller subproblems, solving the subproblems recursively, and combining the solutions. It provides examples of divide and conquer algorithms like merge sort, quicksort, and binary search. Merge sort works by recursively sorting halves of an array until it is fully sorted. Quicksort selects a pivot element and partitions the array into subarrays of smaller and larger elements, recursively sorting the subarrays. Binary search recursively searches half-intervals of a sorted array to find a target value.
Data Structure and Algorithms.pptx
Data Structure and Algorithms.pptxSyed Zaid Irshad The document provides an outline for a course on data structures and algorithms. It includes topics like data types and operations, time-space tradeoffs, algorithm development, asymptotic notations, common data structures, sorting and searching algorithms, and linked lists. The course will use Google Classroom and have assignments, quizzes, and a final exam.
Dinive conquer algorithm
Dinive conquer algorithmMohd Arif The document discusses the divide and conquer algorithm design technique. It begins by explaining the basic approach of divide and conquer which is to (1) divide the problem into subproblems, (2) conquer the subproblems by solving them recursively, and (3) combine the solutions to the subproblems into a solution for the original problem. It then provides merge sort as a specific example of a divide and conquer algorithm for sorting a sequence. It explains that merge sort divides the sequence in half recursively until individual elements remain, then combines the sorted halves back together to produce the fully sorted sequence.
Algorithms Lecture 8: Pattern Algorithms
Algorithms Lecture 8: Pattern AlgorithmsMohamed Loey The document discusses patterns in algorithms, particularly focusing on pattern searching techniques used in computer science. It explains naive pattern searching, provides examples of inputs and outputs, and outlines regular expressions for matching text patterns. Additionally, it covers best and worst-case scenarios for pattern searching and demonstrates the use of Python for regular expressions.
Complexity of Algorithm
Complexity of AlgorithmMuhammad Muzammal This document discusses the complexity of algorithms and the tradeoff between algorithm cost and time. It defines algorithm complexity as a function of input size that measures the time and space used by an algorithm. Different complexity classes are described such as polynomial, sub-linear, and exponential time. Examples are given to find the complexity of bubble sort and linear search algorithms. The concept of space-time tradeoffs is introduced, where using more space can reduce computation time. Genetic algorithms are proposed to efficiently solve large-scale construction time-cost tradeoff problems.
Asymptotic Notation and Complexity
Asymptotic Notation and ComplexityRajandeep Gill The document discusses the analysis of algorithms, focusing on their running time and factors affecting it, such as memory usage and programmer effort. It outlines different types of analysis, including worst case, best case, and average case, as well as asymptotic notation used to compare algorithms. Key concepts include the growth rates of functions and various notations like Big-O, Big-Omega, and Big-Theta to classify algorithm complexity.
Data structures and algorithms
Data structures and algorithmsJulie Iskander The document covers data structures and algorithms, outlining key topics such as sorting (selection sort, bubble sort, merge sort) and searching algorithms (linear search, binary search) alongside their complexities. It describes various data structures, including arrays, linked lists, stacks, queues, and trees, highlighting their characteristics and operations. Additionally, it emphasizes the importance of algorithm analysis, discussing time and space complexities and providing implementation examples in C.
Solving recurrences
Solving recurrencesMegha V The document discusses methods for solving recurrences in algorithms, focusing on recursive and non-recursive algorithms. It presents various techniques such as the iteration method, substitution method, recursion tree method, and the master theorem, illustrated with examples. The content emphasizes finding explicit formulas for recurrences and understanding their running time in relation to algorithmic efficiency.
Algorithm Complexity and Main Concepts
Algorithm Complexity and Main ConceptsAdelina Ahadova An algorithm is a finite set of instructions to accomplish a predefined task. Performance of an algorithm is measured by its time and space complexity, with common metrics being big O, big Omega, and big Theta notation. Common data structures include arrays, linked lists, stacks, queues, trees and graphs. Key concepts are asymptotic analysis of algorithms, recursion, and analyzing complexity classes like constant, linear, quadratic and logarithmic time.
Unit 1 chapter 1 Design and Analysis of Algorithms
Unit 1 chapter 1 Design and Analysis of AlgorithmsP. Subathra Kishore, KAMARAJ College of Engineering and Technology, Madurai The document introduces algorithms, outlining their definition, design, and implementation steps while highlighting important problem types and fundamental data structures. It explains the concept of algorithms through examples like finding the greatest common divisor (gcd) and generating prime numbers. The document also touches on algorithm efficiency, correctness, and various problem-solving techniques.
Design and Analysis of Algorithms
Design and Analysis of AlgorithmsSwapnil Agrawal The document discusses the analysis of algorithms. It begins by defining an algorithm and describing different types. It then covers analyzing algorithms in terms of correctness, time efficiency, space efficiency, and optimality through theoretical and empirical analysis. The document discusses analyzing time efficiency by determining the number of repetitions of basic operations as a function of input size. It provides examples of input size, basic operations, and formulas for counting operations. It also covers analyzing best, worst, and average cases and establishes asymptotic efficiency classes. The document then analyzes several examples of non-recursive and recursive algorithms.
Daa unit 1
Daa unit 1Abhimanyu Mishra The document discusses algorithms and their analysis. It covers:
1) The definition of an algorithm and its key characteristics like being unambiguous, finite, and efficient.
2) The fundamental steps of algorithmic problem solving like understanding the problem, designing a solution, and analyzing efficiency.
3) Methods for specifying algorithms using pseudocode, flowcharts, or natural language.
4) Analyzing an algorithm's time and space efficiency using asymptotic analysis and orders of growth like best-case, worst-case, and average-case scenarios.
Lecture 4 asymptotic notations
Lecture 4 asymptotic notationsjayavignesh86 This document discusses asymptotic notations and their use in analyzing the time complexity of algorithms. It introduces the Big-O, Big-Omega, and Big-Theta notations for describing the asymptotic upper bound, lower bound, and tight bound of an algorithm's running time. The document explains that asymptotic notations allow algorithms to be compared by ignoring lower-order terms and constants, and focusing on the highest-order term that dominates as the input size increases. Examples are provided to illustrate the different orders of growth and the notations used to describe them.
Asymptotic notations
Asymptotic notationsNikhil Sharma The document discusses asymptotic notations that are used to describe the time complexity of algorithms. It introduces big O notation, which describes asymptotic upper bounds, big Omega notation for lower bounds, and big Theta notation for tight bounds. Common time complexities are described such as O(1) for constant time, O(log N) for logarithmic time, and O(N^2) for quadratic time. The notations allow analyzing how efficiently algorithms use resources like time and space as the input size increases.
Binary search
Binary searchAparnaKumari31 Binary search is an algorithm that finds the position of a target value within a sorted array. It works by recursively dividing the array range in half and searching only within the appropriate half. The time complexity is O(log n) in the average and worst cases and O(1) in the best case, making it very efficient for searching sorted data. However, it requires the list to be sorted for it to work.
Graph coloring using backtracking
Graph coloring using backtrackingshashidharPapishetty This document summarizes graph coloring using backtracking. It defines graph coloring as minimizing the number of colors used to color a graph. The chromatic number is the fewest colors needed. Graph coloring is NP-complete. The document outlines a backtracking algorithm that tries assigning colors to vertices, checks if the assignment is valid (no adjacent vertices have the same color), and backtracks if not. It provides pseudocode for the algorithm and lists applications like scheduling, Sudoku, and map coloring.
how to calclute time complexity of algortihm
how to calclute time complexity of algortihmSajid Marwat This document discusses algorithm analysis and complexity. It defines key terms like asymptotic complexity, Big-O notation, and time complexity. It provides examples of analyzing simple algorithms like a sum function to determine their time complexity. Common analyses include looking at loops, nested loops, and sequences of statements. The goal is to classify algorithms according to their complexity, which is important for large inputs and machine-independent. Algorithms are classified based on worst, average, and best case analyses.
Unit 1 chapter 1 Design and Analysis of Algorithms
Unit 1 chapter 1 Design and Analysis of AlgorithmsP. Subathra Kishore, KAMARAJ College of Engineering and Technology, Madurai
Viewers also liked (6)
Computer Security Lecture 5: Simplified Advanced Encryption Standard
Computer Security Lecture 5: Simplified Advanced Encryption StandardMohamed Loey The document provides an overview of the Simplified Advanced Encryption Standard (S-AES), created for educational purposes to help students understand encryption and decryption processes. It details the methods for key generation, block encryption, and decryption using 16-bit keys and plaintext, along with step-by-step transformations such as nibble substitution, row shifting, and column mixing. S-AES allows students to perform encryption operations manually, enhancing their comprehension of the underlying structure of AES.
Deep Learning - Overview of my work II
Deep Learning - Overview of my work IIMohamed Loey The document covers various aspects of deep learning, including definitions of artificial narrow, general, and super intelligence, and details on machine learning techniques like supervised and unsupervised learning. It discusses the architecture of neural networks such as convolutional neural networks and their application in image recognition, speech recognition, and natural language processing, along with datasets like MNIST and CIFAR-10. Techniques to mitigate overfitting in neural networks, such as dropout and L2 regularization, are also highlighted, along with a summary of a new CNN architecture built for classifying Arabic handwritten characters.
PMP Lecture 1: Introduction to Project Management
PMP Lecture 1: Introduction to Project ManagementMohamed Loey The document provides an introduction to project management, detailing its history, key concepts, and applications in various contexts. It defines projects as temporary endeavors aimed at producing unique results and emphasizes the roles of program management, portfolio management, and project management offices. Additionally, it introduces the Project Management Body of Knowledge (PMBOK) and the Project Management Institute (PMI), highlighting certification options and organizational details.
Computer Security Lecture 7: RSA
Computer Security Lecture 7: RSAMohamed Loey RSA is a widely used asymmetric encryption algorithm, named after its inventors Ron Rivest, Adi Shamir, and Leonard Adleman. It involves a key generation process using two prime numbers to create public and private keys for secure communication. It provides methods for encryption and decryption, along with potential security challenges such as brute force attacks and mathematical vulnerabilities.
Convolutional Neural Network Models - Deep Learning
Convolutional Neural Network Models - Deep LearningMohamed Loey The document provides an overview of Convolutional Neural Network (CNN) models developed for image classification, highlighting notable models such as AlexNet, ZFNet, VGGNet, GoogLeNet, and ResNet. It outlines the architecture, training processes, and performance metrics of these models, including their respective top-5 error rates in the ImageNet Large Scale Visual Recognition Challenge. Additionally, it covers specific training techniques and innovations employed by each model to improve accuracy and efficiency.
C++ Programming Language
C++ Programming Language Mohamed Loey The document provides an extensive overview of the C++ programming language, covering fundamental concepts such as variables, data types, expressions, and control structures like conditional statements and loops. It includes examples of basic C++ code, demonstrating key functionalities like namespaces, operations, and user inputs. Additionally, it delves into more advanced topics like arrays, strings, and various types of operators used in C++ programming.
Ad
Similar to Algorithms Lecture 3: Analysis of Algorithms II (20)
3 analysis.gtm
3 analysis.gtmNatarajan Angappan This document discusses algorithm analysis and asymptotic notation. It introduces algorithms for computing prefix averages in arrays. One algorithm runs in quadratic time O(n^2) by applying the definition directly. A more efficient linear time O(n) algorithm is also presented that maintains a running sum. Asymptotic analysis determines the worst-case running time of an algorithm as a function of the input size using big-O notation. This provides an analysis of algorithms that is independent of implementation details and hardware.
Ch24 efficient algorithms
Ch24 efficient algorithmsrajatmay1992 This document discusses analyzing the efficiency of algorithms. It begins by explaining how to measure algorithm efficiency using Big O notation, which estimates how fast an algorithm's execution time grows as the input size increases. Common growth rates like constant, logarithmic, linear, and quadratic time are described. Examples are provided to demonstrate determining the Big O of various algorithms. Specific algorithms analyzed in more depth include binary search, selection sort, insertion sort, and Towers of Hanoi. The document aims to introduce techniques for developing efficient algorithms using approaches like dynamic programming, divide-and-conquer, and backtracking.
AoA Lec Design of algorithm spresentation
AoA Lec Design of algorithm spresentationHamzaSadaat The document outlines the objectives, outcomes, and content of an advanced algorithms design and analysis course, emphasizing algorithm complexity analysis, design techniques, and problem-solving strategies. Key topics include asymptotic notation, algorithm properties, and various algorithm design approaches such as brute force, greedy, and dynamic programming. Additionally, it covers algorithm performance measurement through running time analysis and space utilization, alongside resources for further study.
Analysis of algo
Analysis of algoSandeep Bhargava The document discusses analyzing the efficiency of algorithms. It notes that algorithms can be correct but the best depends on efficiency. Efficiency depends on time and space complexity, where time complexity is the amount of time needed for complete execution and space complexity is the amount of memory required. Different algorithms have different efficiencies that can be analyzed based on how processing time and memory usage increase with larger input sizes.
Data Structures and Agorithm: DS 22 Analysis of Algorithm.pptx
Data Structures and Agorithm: DS 22 Analysis of Algorithm.pptxRashidFaridChishti The document is a comprehensive lecture on algorithms, specifically analyzing their efficiency and performance, including time and space complexity. It covers important concepts like correct algorithms, data structures, growth rates, and asymptotic notations (Big O, Big Omega, and Big Theta). The lecture emphasizes the need for mathematical analysis and experimental studies to evaluate and compare algorithms objectively.
Chapter one
Chapter onemihiretu kassaye The document provides an overview of algorithms and data structures. It discusses what an algorithm is, different algorithm design strategies, approaches to analyzing algorithms, and key computational problems like sorting, searching, and graph problems. It also covers fundamental data structures like lists, stacks, queues, and trees. Major sections include introductions to algorithms, analysis of algorithms, problem solving techniques, and linear and non-linear data structures.
Data Structures and Algorithms Lecture 2: Analysis of Algorithms, Asymptotic ...
Data Structures and Algorithms Lecture 2: Analysis of Algorithms, Asymptotic ...TechVision8 This document discusses analyzing the running time of algorithms. It introduces pseudocode as a way to describe algorithms, primitive operations that are used to count the number of basic steps an algorithm takes, and asymptotic analysis to determine an algorithm's growth rate as the input size increases. The key points covered are using big-O notation to focus on the dominant term and ignore lower-order terms and constants, and analyzing two algorithms for computing prefix averages to demonstrate asymptotic analysis.
Advanced Datastructures and algorithms CP4151unit1b.pdf
Advanced Datastructures and algorithms CP4151unit1b.pdfSheba41 Insertion sort has a running time of O(n^2) in the worst case. It works by iterating through the array (n times) and inserting each element into its sorted position (taking up to n steps). This results in a total worst case time of n(n) = O(n^2) operations.
Analysis.ppt
Analysis.pptShivaniSharma335055 This document discusses analysis of algorithms and asymptotic notation. It introduces key concepts like worst case running time, pseudo-code, experimental studies and their limitations, asymptotic notation like Big-O, and using asymptotic analysis to evaluate an algorithm's efficiency based on input size independently of hardware. Examples are provided to illustrate counting primitive operations and analyzing algorithms' asymptotic running times as O(log n), O(n), O(n^2) etc.
Lec1
Lec1Anjneya Varshney Data structures and algorithms involve organizing data to solve problems efficiently. An algorithm describes computational steps, while a program implements an algorithm. Key aspects of algorithms include efficiency as input size increases. Experimental studies measure running time but have limitations. Pseudocode describes algorithms at a high level. Analysis counts primitive operations to determine asymptotic running time, ignoring constant factors. The best, worst, and average cases analyze efficiency. Asymptotic notation like Big-O simplifies analysis by focusing on how time increases with input size.
Unit 2 algorithm
Unit 2 algorithmDabbal Singh Mahara This document provides an overview of algorithms. It begins by discussing the origins and evolution of the term "algorithm" from its Arabic roots in the 9th century to its modern meaning of a well-defined computational procedure. The document then defines algorithms and their key characteristics such as being precise, unambiguous, and terminating after a finite number of steps. Common algorithm design techniques like divide-and-conquer, greedy algorithms, and dynamic programming are introduced. Examples of merge sort and finding the maximum element in a list are used to illustrate algorithm concepts.
Annotations.pdf
Annotations.pdfGauravKumar295392 Asymptotic analysis allows the comparison of algorithms based on how their running time grows with input size rather than experimental testing. It involves analyzing an algorithm's pseudo-code to count primitive operations and expressing the running time using asymptotic notation like O(f(n)) which ignores constants. Common time complexities include constant O(1), logarithmic O(log n), linear O(n), quadratic O(n^2), and exponential O(2^n). Faster algorithms have lower asymptotic complexity.
Cis435 week01
Cis435 week01ashish bansal This document provides an introduction to algorithms and algorithm analysis. It defines what an algorithm is, provides examples, and discusses analyzing algorithms to determine their efficiency. Insertion sort and merge sort are presented as examples and their time complexities are analyzed. Asymptotic notation is introduced to describe an algorithm's order of growth and provide bounds on its running time. Key points covered include analyzing best-case and worst-case time complexities, using recurrences to model algorithms, and the properties of asymptotic notation. Homework problems are assigned from the textbook chapters.
Algorithm Design and Analysis
Algorithm Design and AnalysisSayed Chhattan Shah The document provides an extensive overview of algorithm design and analysis, highlighting the importance of algorithms in computer science. It covers fundamental concepts, characteristics of algorithms, different sorting techniques, and explores computational complexity in terms of time and space. Additionally, it discusses strategies for analyzing algorithms, including experimental approaches and asymptotic analysis.
Lec1
Lec1Nikhil Chilwant The document discusses data structures and algorithms. It defines key concepts like algorithms, programs, data structures, and asymptotic analysis. It explains how to analyze algorithms to determine their efficiency, including analyzing best, worst, and average cases. Common notations for describing asymptotic running time like Big-O, Big-Omega, and Big-Theta are introduced. The document provides examples of analyzing sorting algorithms like insertion sort and calculating running times. It also discusses techniques for proving an algorithm's correctness like assertions and loop invariants.
Algorithm for the DAA agscsnak javausmagagah
Algorithm for the DAA agscsnak javausmagagahRaviPandey598038 The document provides an in-depth overview of algorithms, analyzing their characteristics, types, and complexities, including time and space efficiency. It covers methods for analyzing algorithms, including worst, best, and average case scenarios, and introduces asymptotic notations such as big O, big Omega, and big Theta for evaluating algorithm performance. Additionally, it discusses algorithm design techniques and the concept of time-space trade-offs, emphasizing the importance of selecting appropriate algorithms based on their efficiency and complexity.
asymptotic analysis and insertion sort analysis
asymptotic analysis and insertion sort analysisAnindita Kundu This document discusses asymptotic analysis of algorithms. It introduces key concepts like algorithms, data structures, best/average/worst case running times, and asymptotic notations like Big-O, Big-Omega, and Big-Theta. These notations are used to describe the long-term growth rates of functions and provide upper/lower/tight bounds on the running time of algorithms as the input size increases. Examples show how to analyze the asymptotic running time of algorithms like insertion sort, which is O(n^2) in the worst case but O(n) in the best case.
Data Structure - Lecture 1 - Introduction.pdf
Data Structure - Lecture 1 - Introduction.pdfdonotreply20 The document outlines a course on data structures, highlighting their importance in efficiently organizing and manipulating data for complex applications. It covers various data structures, algorithm analysis, and provides examples to illustrate efficiency differences between algorithms. The course requires programming experience in C/C++, and students will learn about topics like algorithm analysis, stacks, trees, and graph algorithms.
Ad
More from Mohamed Loey (18)
Lecture 6: Deep Learning Applications
Lecture 6: Deep Learning ApplicationsMohamed Loey The document outlines various applications of deep learning in fields such as natural language processing, image and video processing, and biomedical imaging. It emphasizes tasks including text classification, machine translation, image segmentation, and anomaly classification. Additionally, it provides contact information for further inquiries.
Lecture 5: Convolutional Neural Network Models
Lecture 5: Convolutional Neural Network ModelsMohamed Loey The document outlines the evolution and architecture of various convolutional neural networks (CNNs) developed for the ImageNet Large Scale Visual Recognition Challenge (ILSVRC) from 2012 to 2015, focusing on models like AlexNet, ZFNet, VGGNet, GoogLeNet, and ResNet. It describes key features such as layer compositions, error rates, and innovations like dropout and batch normalization aimed at improving performance and reducing overfitting. Each network's structure is compared, highlighting advancements in design and training techniques, culminating in the increasing complexity and depth of models over the years.
Lecture 4: Deep Learning Frameworks
Lecture 4: Deep Learning FrameworksMohamed Loey The document provides information on several popular deep learning frameworks: TensorFlow, Caffe, Theano, Torch, CNTK, and Keras. It describes each framework's creator, license, programming languages supported, and brief purpose or use. TensorFlow is noted as the most popular framework, created by Google for machine learning research. Caffe is described as the fastest, Theano as most efficient, Torch is used by Facebook AI, CNTK for high scalability, and Keras for easy experimentation across frameworks. The document also provides examples of building and running computational graphs in TensorFlow.
Lecture 4: How it Works: Convolutional Neural Networks
Lecture 4: How it Works: Convolutional Neural NetworksMohamed Loey The document contains a large two-dimensional array representing a grid of values, composed of pixels denoted by 'x', 'o', and numerical values including -1 and 1. It appears to focus on patterns or clusters within the grid, potentially related to image processing or game mechanics. The specific context or application of this matrix is not provided.
Lecture 3: Convolutional Neural Networks
Lecture 3: Convolutional Neural NetworksMohamed Loey The document discusses convolutional neural networks (CNNs), highlighting their structure and applications in image and speech recognition while outlining the importance of deep learning in machine learning. It details the various layers of CNNs, prominent architectures such as AlexNet and VGGNet, and the datasets used for training and evaluation. Additionally, it covers strategies to mitigate overfitting in CNNs and emphasizes the significance of deep learning for complex tasks in data science.
Lecture 2: Artificial Neural Network
Lecture 2: Artificial Neural NetworkMohamed Loey The document provides an overview of artificial neural networks (ANNs), detailing their structure and functionality, inspired by biological neurons. It discusses the perceptron model and its limitations, such as its inability to solve nonlinear problems like XOR, and presents multilayer perceptrons with backpropagation as a solution. Additionally, it outlines key concepts and methods related to neural networks, including forward propagation, backpropagation, and error minimization in training, while also mentioning a practical assignment related to neural network architectures.
Lecture 1: Deep Learning for Computer Vision
Lecture 1: Deep Learning for Computer VisionMohamed Loey This document discusses how deep learning has helped advance computer vision capabilities. It notes that deep learning can help bridge the gap between pixels and meaning by allowing computers to recognize complex patterns in images. It provides an overview of related fields like image processing, machine learning, artificial intelligence, and computer graphics. It also lists some specific applications of deep learning like object detection, image classification, and generating descriptive text. Students are then assigned a task to research how deep learning has improved one particular topic and submit a two-page summary.
Design of an Intelligent System for Improving Classification of Cancer Diseases
Design of an Intelligent System for Improving Classification of Cancer DiseasesMohamed Loey The document presents an intelligent decision support system designed for the early diagnosis of cancer by classifying gene expression profiles from datasets related to breast, colon, and central nervous system (CNS) cancers. The system overcomes challenges such as dimensionality and relevancy of gene data, utilizing advanced methodologies like information gain for feature selection and gray wolf optimization for feature reduction. Results indicate the proposed system has superior classification accuracy compared to existing methodologies, demonstrating a significant improvement in the reliability and efficiency of cancer diagnosis.
Computer Security - CCNA Security - Lecture 2
Computer Security - CCNA Security - Lecture 2Mohamed Loey The document covers various aspects of network security, specifically focusing on authentication, authorization, and accounting (AAA) processes essential for effective network management. It discusses methods for implementing AAA, including local and server-based authentication, and explains protocols like TACACS+ and RADIUS used in these processes. Additionally, it highlights best practices for configuring AAA in different network environments, emphasizing the importance of securing access to network resources.
Computer Security - CCNA Security - Lecture 1
Computer Security - CCNA Security - Lecture 1Mohamed Loey The document provides an overview of modern network security threats and methods for securing network devices, including various types of attacks such as denial of service, man-in-the-middle, and phishing. It also discusses the implementation of security measures such as firewalls, intrusion prevention, and cryptographic systems. Additionally, it highlights tools like Kali Linux and Wireshark for penetration testing and network analysis.
Computer Security Lecture 4.1: DES Supplementary Material
Computer Security Lecture 4.1: DES Supplementary MaterialMohamed Loey The document discusses the DES (Data Encryption Standard) encryption algorithm, detailing its processes including initial and final permutations, key shifts, and S-boxes. It provides a systematic breakdown of the encryption rounds and permutations involved, showing how plaintext is transformed into ciphertext using specific bit manipulations. Various tables and key schedules are included to illustrate the steps and components necessary for executing the algorithm.
PMP Lecture 4: Project Integration Management
PMP Lecture 4: Project Integration ManagementMohamed Loey Project integration management encompasses the processes to identify, define, and coordinate the various project management activities. Key components include developing the project charter, project management plan, executing work, and monitoring and controlling project performance. The overall goal is to ensure a cohesive approach to managing a project effectively, culminating in successful project closure.
Computer Security Lecture 4: Block Ciphers and the Data Encryption Standard
Computer Security Lecture 4: Block Ciphers and the Data Encryption StandardMohamed Loey The document discusses classical encryption techniques, focusing on the Data Encryption Standard (DES), which is a symmetric-key algorithm for encrypting electronic data using 64-bit blocks and a 56-bit key. It details the processes involved in key creation, encryption, and describes how the algorithm transforms plaintext into ciphertext through a series of steps, including the use of permutations and substitution boxes. DES was developed in the 1970s and was standardized by the National Institute of Standards and Technology (NIST) in 1977.
Computer Security Lecture 3: Classical Encryption Techniques 2
Computer Security Lecture 3: Classical Encryption Techniques 2Mohamed Loey The document discusses classical encryption techniques, focusing on various ciphers such as polyalphabetic ciphers (Vigenère, Autokey, Vernam) and transposition techniques (Rail Fence, Row Transposition). It explains the mechanisms of encryption and decryption, highlighting the mathematical operations involved and providing examples of plaintext transformations. Additionally, it emphasizes the significance of using keys and certain rules to secure data in encryption processes.
Computer Security Lecture 2: Classical Encryption Techniques 1
Computer Security Lecture 2: Classical Encryption Techniques 1Mohamed Loey The document discusses classical encryption techniques, primarily focusing on symmetric encryption methods such as the Caesar cipher, monoalphabetic ciphers, and the Playfair cipher. It outlines the processes involved in encryption and decryption, emphasizing the use of secret keys and transformation algorithms. Examples of application, including encoding and decoding messages, are also provided for better understanding of these techniques.
Computer Security Lecture 1: Overview
Computer Security Lecture 1: OverviewMohamed Loey The document provides a comprehensive overview of cryptography and its role in computer security, detailing its historical background, the CIA triad of confidentiality, integrity, and availability, and encryption mechanisms. It differentiates between symmetric and asymmetric encryption, explaining their properties, applications, and various algorithms used. Additionally, it covers topics such as the OSI security architecture, types of security attacks, and the importance of key management in securing data.
PMP Lecture 3: Project Management Processes
PMP Lecture 3: Project Management ProcessesMohamed Loey The document outlines the categorization of project management processes into five process groups: initiating, planning, executing, monitoring and controlling, and closing. It also describes ten knowledge areas that encompass the essential concepts and activities within project management, including integration, scope, time, cost, quality, human resources, communications, risk, procurement, and stakeholder management. Overall, the text serves as a comprehensive guide to understanding the various processes and knowledge areas necessary for effective project management.
PMP Lecture 2: Project Management Framework
PMP Lecture 2: Project Management FrameworkMohamed Loey The document outlines different organizational structures used in project management, including functional, projectized, and matrix organizations, each with distinct characteristics and implications for project execution. It discusses how these structures influence resource availability, project authority, and overall project management effectiveness. Additionally, it highlights the advantages and disadvantages of each organizational type.
Recently uploaded (20)
Chalukyas of Gujrat, Solanki Dynasty NEP.pptx
Chalukyas of Gujrat, Solanki Dynasty NEP.pptxDr. Ravi Shankar Arya Mahila P. G. College, Banaras Hindu University, Varanasi, India. This presentation has been made keeping in mind the students of undergraduate and postgraduate level. In this slide try to present the brief history of Chaulukyas of Gujrat up to Kumarpala To keep the facts in a natural form and to display the material in more detail, the help of various books, websites and online medium has been taken. Whatever medium the material or facts have been taken from, an attempt has been made by the presenter to give their reference at the end.
Chaulukya or Solanki was one of the Rajputs born from Agnikul. In the Vadnagar inscription, the origin of this dynasty is told from Brahma's Chauluk or Kamandalu. They ruled in Gujarat from the latter half of the tenth century to the beginning of the thirteenth century. Their capital was in Anahilwad. It is not certain whether it had any relation with the Chalukya dynasty of the south or not. It is worth mentioning that the name of the dynasty of the south was 'Chaluky' while the dynasty of Gujarat has been called 'Chaulukya'. The rulers of this dynasty were the supporters and patrons of Jainism.
How to Manage Inventory Movement in Odoo 18 POS
How to Manage Inventory Movement in Odoo 18 POSCeline George Inventory management in the Odoo 18 Point of Sale system is tightly integrated with the inventory module, offering a solution to businesses to manage sales and stock in one united system.
How to Create an Event in Odoo 18 - Odoo 18 Slides
How to Create an Event in Odoo 18 - Odoo 18 SlidesCeline George Creating an event in Odoo 18 is a straightforward process that allows you to manage various aspects of your event efficiently.
Odoo 18 Events Module is a powerful tool for organizing and managing events of all sizes, from conferences and workshops to webinars and meetups.
How to Implement Least Package Removal Strategy in Odoo 18 Inventory
How to Implement Least Package Removal Strategy in Odoo 18 InventoryCeline George In Odoo, the least package removal strategy is a feature designed to optimize inventory management by minimizing the number of packages open to fulfill the orders. This strategy is particularly useful for the business that deals with products packages in various quantities such as boxes, cartons or palettes.
How to Manage Multi Language for Invoice in Odoo 18
How to Manage Multi Language for Invoice in Odoo 18Celine George Odoo supports multi-language functionality for invoices, allowing you to generate invoices in your customers’ preferred languages. Multi-language support for invoices is crucial for businesses operating in global markets or dealing with customers from different linguistic backgrounds.
Paper 107 | From Watchdog to Lapdog: Ishiguro’s Fiction and the Rise of “Godi...
Paper 107 | From Watchdog to Lapdog: Ishiguro’s Fiction and the Rise of “Godi...Rajdeep Bavaliya Dive into a captivating analysis where Kazuo Ishiguro’s nuanced fiction meets the stark realities of post‑2014 Indian journalism. Uncover how “Godi Media” turned from watchdog to lapdog, echoing the moral compromises of Ishiguro’s protagonists. We’ll draw parallels between restrained narrative silences and sensationalist headlines—are our media heroes or traitors? Don’t forget to follow for more deep dives!
M.A. Sem - 2 | Presentation
Presentation Season - 2
Paper - 107: The Twentieth Century Literature: From World War II to the End of the Century
Submitted Date: April 4, 2025
Paper Name: The Twentieth Century Literature: From World War II to the End of the Century
Topic: From Watchdog to Lapdog: Ishiguro’s Fiction and the Rise of “Godi Media” in Post-2014 Indian Journalism
[Please copy the link and paste it into any web browser to access the content.]
Video Link: https://youtu.be/kIEqwzhHJ54
For a more in-depth discussion of this presentation, please visit the full blog post at the following link: https://rajdeepbavaliya2.blogspot.com/2025/04/from-watchdog-to-lapdog-ishiguro-s-fiction-and-the-rise-of-godi-media-in-post-2014-indian-journalism.html
Please visit this blog to explore additional presentations from this season:
Hashtags:
#GodiMedia #Ishiguro #MediaEthics #WatchdogVsLapdog #IndianJournalism #PressFreedom #LiteraryCritique #AnArtistOfTheFloatingWorld #MediaCapture #KazuoIshiguro
Keyword Tags:
Godi Media, Ishiguro fiction, post-2014 Indian journalism, media capture, Kazuo Ishiguro analysis, watchdog to lapdog, press freedom India, media ethics, literature and media, An Artist of the Floating World
Revista digital preescolar en transformación
Revista digital preescolar en transformaciónguerragallardo26 EVOLUCIÓN DEL CONTENIDO DE LA EVALUACIÓN DE LOS RECURSOS Y DE LA FORMACIÓN DE LOS DOCENTES
Overview of Off Boarding in Odoo 18 Employees
Overview of Off Boarding in Odoo 18 EmployeesCeline George When an employee leaves the company, Odoo provides a streamlined offboarding process to ensure all necessary steps are taken.
Assisting Individuals and Families to Promote and Maintain Health – Unit 7 | ...
Assisting Individuals and Families to Promote and Maintain Health – Unit 7 | ...RAKESH SAJJAN This PowerPoint presentation is based on Unit 7 – Assisting Individuals and Families to Promote and Maintain Their Health, a core topic in Community Health Nursing – I for 5th Semester B.Sc Nursing students, as per the Indian Nursing Council (INC) guidelines.
The unit emphasizes the nurse’s role in family-centered care, early detection of health problems, health promotion, and appropriate referrals, especially in the context of home visits and community outreach. It also strengthens the student’s understanding of nursing responsibilities in real-life community settings.
📘 Key Topics Covered in the Presentation:
Introduction to family health care: needs, principles, and objectives
Assessment of health needs of individuals, families, and groups
Observation and documentation during home visits and field assessments
Identifying risk factors: environmental, behavioral, genetic, and social
Conducting growth and development monitoring in infants and children
Recording and observing:
Milestones of development
Menstrual health and reproductive cycle
Temperature, blood pressure, and vital signs
General physical appearance and personal hygiene
Social assessment: understanding family dynamics, occupation, income, living conditions
Health education and counseling for individuals and families
Guidelines for early detection and referral of communicable and non-communicable diseases
Maintenance of family health records and individual health cards
Assisting families with:
Maternal and child care
Elderly and chronic disease management
Hygiene and nutrition guidance
Utilization of community resources – referral linkages, support services, and local health programs
Role of nurse in coordinating care, advocating for vulnerable individuals, and empowering families
Promoting self-care and family participation in disease prevention and health maintenance
This presentation is highly useful for:
Nursing students preparing for internal exams, university theory papers, or community postings
Health educators conducting family teaching sessions
Students conducting fieldwork and project work during community postings
Public health nurses and outreach workers dealing with preventive, promotive, and rehabilitative care
It’s structured in a step-by-step format, featuring tables, case examples, and simplified explanations tailored for easy understanding and classroom delivery.
Capitol Doctoral Presentation -June 2025.pptx
Capitol Doctoral Presentation -June 2025.pptxCapitolTechU Slides from a Capitol Technology University presentation covering doctoral programs offered by the university. All programs are online, and regionally accredited. The presentation covers degree program details, tuition, financial aid and the application process.
Non-Communicable Diseases and National Health Programs – Unit 10 | B.Sc Nursi...
Non-Communicable Diseases and National Health Programs – Unit 10 | B.Sc Nursi...RAKESH SAJJAN This PowerPoint presentation is prepared for Unit 10 – Non-Communicable Diseases and National Health Programs, as per the 5th Semester B.Sc Nursing syllabus outlined by the Indian Nursing Council (INC) under the subject Community Health Nursing – I.
This unit focuses on equipping students with knowledge of the causes, prevention, and control of non-communicable diseases (NCDs), which are a major public health challenge in India. The presentation emphasizes the nurse’s role in early detection, screening, management, and referral services under national-level programs.
🔹 Key Topics Included:
Definition, burden, and impact of NCDs in India
Epidemiology, risk factors, signs/symptoms, prevention, and management of:
Diabetes Mellitus
Hypertension
Cardiovascular Diseases
Stroke & Obesity
Thyroid Disorders
Blindness
Deafness
Injuries and Accidents (incl. road traffic injuries and trauma guidelines)
NCD-2 Cancers:
Breast Cancer
Cervical Cancer
Oral Cancer
Risk factors, screening, diagnosis, early signs, referral & palliative care
Role of nurse in screening, referral, counseling, and continuum of care
National Programs:
National Program for Prevention and Control of Cancer, Diabetes, Cardiovascular Diseases and Stroke (NPCDCS)
National Program for Control of Blindness
National Program for Prevention and Control of Deafness
National Tobacco Control Program (NTCP)
Introduction to Universal Health Coverage and Ayushman Bharat
Use of standard treatment protocols and referral flowcharts
This presentation is ideal for:
Classroom lectures, field assignments, health education planning, and student projects
Preparing for university exams, class tests, and community field postings
Measuring, learning and applying multiplication facts.
Measuring, learning and applying multiplication facts.cgilmore6 Slides from a presentation by Professor Camilla Gilmore to the Association of Teachers of Mathematics and Mathematics Association Primary Interest group in June 2025.
This gave an overview of two studies that investigated children's multiplication fact knowledge. These studies were part of the SUM research project based at the University of Nottingham and Loughborough University. For more information see www.sumproject.org.uk
Ray Dalio How Countries go Broke the Big Cycle
Ray Dalio How Countries go Broke the Big CycleDadang Solihin A complete and practical understanding of the Big Debt Cycle. A much more practical understanding of how supply and demand really work compared to the conventional economic thinking. A complete and practical understanding of the Overall Big Cycle, which is driven by the Big Debt Cycle and the other major cycles, including the big political cycle within countries that changes political orders and the big geopolitical cycle that changes world orders.
Publishing Your Memoir with Brooke Warner
Publishing Your Memoir with Brooke WarnerBrooke Warner Brooke Warner presents on getting published - traditional, hybrid, and self-publishing.
www.memoirnation.com
2025 June Year 9 Presentation: Subject selection.pptx
2025 June Year 9 Presentation: Subject selection.pptxmansk2 2025 June Year 9 Presentation: Subject selection
How to Manage & Create a New Department in Odoo 18 Employee
How to Manage & Create a New Department in Odoo 18 EmployeeCeline George In Odoo 18's Employee module, organizing your workforce into departments enhances management and reporting efficiency. Departments are a crucial organizational unit within the Employee module.
ABCs of Bookkeeping for Nonprofits TechSoup.pdf
ABCs of Bookkeeping for Nonprofits TechSoup.pdfTechSoup Accounting can be hard enough if you haven’t studied it in school. Nonprofit accounting is actually very different and more challenging still.
Need help? Join Nonprofit CPA and QuickBooks expert Gregg Bossen in this first-time webinar and learn the ABCs of keeping books for a nonprofit organization.
Key takeaways
* What accounting is and how it works
* How to read a financial statement
* What financial statements should be given to the board each month
* What three things nonprofits are required to track
What features to use in QuickBooks to track programs and grants
LDMMIA GRAD Student Check-in Orientation Sampler
LDMMIA GRAD Student Check-in Orientation SamplerLDM & Mia eStudios Completed Tuesday June 10th.
An Orientation Sampler of 8 pages.
It helps to understand the text behind anything. This improves our performance and confidence.
Your training will be mixed media. Includes Rehab Intro and Meditation vods, all sold separately.
Editing our Vods & New Shop.
Retail under $30 per item. Store Fees will apply. Digital Should be low cost.
I am still editing the package. I wont be done until probably July? However; Orientation and Lecture 1 (Videos) will be available soon. Media will vary between PDF and Instruction Videos.
Thank you for attending our free workshops. Those can be used with any Reiki Yoga training package. Traditional Reiki does host rules and ethics. Its silent and within the JP Culture/Area/Training/Word of Mouth. It allows remote healing but there’s limits for practitioners and masters. We are not allowed to share certain secrets/tools. Some content is designed only for “Masters”. Some yoga are similar like the Kriya Yoga-Church (Vowed Lessons). We will review both Reiki and Yoga (Master symbols) later on. Sounds Simple but these things host Energy Power/Protection.
Imagine This package will be a supplement or upgrade for professional Reiki. You can create any style you need.
♥♥♥
•* ́ ̈ ̧.•
(Job) Tech for students: In short, high speed is essential. (Space, External Drives, virtual clouds)
Fast devices and desktops are important. Please upgrade your technology and office as needed and timely. - MIA J. Tech Dept (Timeless)
♥♥♥
•* ́ ̈ ̧.•
Copyright Disclaimer 2007-2025+: These lessons are not to be copied or revised without the
Author’s permission. These Lessons are designed Rev. Moore to instruct and guide students on the path to holistic health and wellness.
It’s about expanding your Nature Talents, gifts, even Favorite Hobbies.
♥♥♥
•* ́ ̈ ̧.•
First, Society is still stuck in the matrix. Many of the spiritual collective, say the matrix crashed. Its now collapsing. This means anything lower, darker realms, astral, and matrix are below 5D. 5D is thee trend. It’s our New Dimensional plane. However; this plane takes work ethic,
integration, and self discovery. ♥♥♥
•* ́ ̈ ̧.•
We don’t need to slave, mule, or work double shifts to fuse Reiki lol. It should blend naturally within our lifestyles. Same with Yoga. There’s no
need to use all the poses/asanas. For under a decade, my fav exercises are not asanas but Pilates. It’s all about Yoga-meditation when using Reiki. (Breaking old myths.)
Thank You for reading our Orientation Sampler. The Workshop is 14 pages on introduction. These are a joy and effortless to produce/make.
Chalukyas of Gujrat, Solanki Dynasty NEP.pptx
Chalukyas of Gujrat, Solanki Dynasty NEP.pptxDr. Ravi Shankar Arya Mahila P. G. College, Banaras Hindu University, Varanasi, India.
Algorithms Lecture 3: Analysis of Algorithms II
- 1. Analysis and Design of Algorithms Analysis of Algorithms II
- 2. Analysis and Design of Algorithms Maximum Pairwise Product Fibonacci Greatest Common Divisors
- 3. Analysis and Design of Algorithms Maximum Pairwise Product
- 4. Analysis and Design of Algorithms Given a sequence of non-negative integers a0,…,an−1, find the maximum pairwise product, that is, the largest integer that can be obtained by multiplying two different elements from the sequence (or, more formally, max aiaj where 0≤i≠j≤n−1). Different elements here mean ai and aj with i≠j (it can be the case that ai=aj).
- 5. Analysis and Design of Algorithms Constraints 2≤n≤2 * 105 & 0≤a0,…,an−1≤105.
- 6. Analysis and Design of Algorithms Sample 1 Input: 1 2 3 Output:6 Sample 2 Input: 7 5 14 2 8 8 10 1 2 3 Output:140
- 7. Analysis and Design of Algorithms Sample 3 Input: 4 6 2 6 1 Output:36
- 8. Analysis and Design of Algorithms Assume the following array 2 4 3 5 1
- 9. Analysis and Design of Algorithms Assume the following array 2 4 3 5 1 i j Result=0
- 10. Analysis and Design of Algorithms Assume the following array 2 4 3 5 1 i j If a[i]*a[j] > result result=a[i]*a[j]=8
- 11. Analysis and Design of Algorithms Assume the following array 2 4 3 5 1 i j If a[i]*a[j] > result result=8
- 12. Analysis and Design of Algorithms Assume the following array 2 4 3 5 1 i j If a[i]*a[j] > result result= a[i]*a[j] =10
- 13. Analysis and Design of Algorithms Naive algorithm
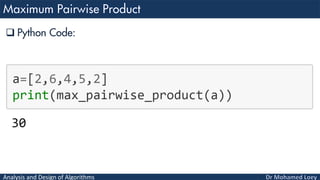
- 14. Analysis and Design of Algorithms Python Code:
- 15. Analysis and Design of Algorithms Time complexity O(n2)
- 16. Analysis and Design of Algorithms we need a faster algorithm. This is because our program performs about n2 steps on a sequence of length n. For the maximal possible value n=200,000 = 2*105, the number of steps is 40,000,000,000 = 4*1010. This is too much. Recall that modern machines can perform roughly 109 basic operations per second
- 17. Analysis and Design of Algorithms Assume the following array 2 4 3 5 1
- 18. Analysis and Design of Algorithms Find maximum number1 2 4 3 5 1 max1
- 19. Analysis and Design of Algorithms Find maximum number2 but not maximum number1 2 4 3 5 1 max2 max1
- 20. Analysis and Design of Algorithms Find maximum number2 but not maximum number1 2 4 3 5 1 max2 max1 return max1*max2
- 21. Analysis and Design of Algorithms Efficient algorithm
- 22. Analysis and Design of Algorithms Efficient algorithm
- 23. Analysis and Design of Algorithms Time complexity O(n)
- 24. Analysis and Design of Algorithms Fibonacci
- 25. Analysis and Design of Algorithms 0,1,1,2,3,5,8,13,21,34, …
- 26. Analysis and Design of Algorithms Definition: 𝐹𝑛 = 0 𝑛 = 0 1 𝑛 = 1 𝐹𝑛−2 + 𝐹𝑛−1 𝑛 > 1
- 27. Analysis and Design of Algorithms Examples: 𝐹8 = 21 𝐹20 = 6765 𝐹50 = 12586269025 𝐹100 = 354224848179261915075
- 28. Analysis and Design of Algorithms Examples: 𝐹500 = 1394232245616978801397243828 7040728395007025658769730726 4108962948325571622863290691 557658876222521294125
- 29. Analysis and Design of Algorithms Naive algorithm
- 30. Analysis and Design of Algorithms Naive algorithm Very Long Time why????
- 31. Analysis and Design of Algorithms
- 32. Analysis and Design of Algorithms
- 33. Analysis and Design of Algorithms F6 F5 F4 F3 F2 F1 F0 F0 F1 F0 F2 F1 F0 F0 F3 F2 F1 F0 F0 F1 F0 F4 F3 F2 F1 F0 F0 F1 F0 F2 F1 F0 F0
- 34. Analysis and Design of Algorithms Fib algorithm is very slow because of recursion Time complexity = O(2n)
- 35. Analysis and Design of Algorithms Efficient algorithm 0 1 1 2 3 5 Create array then insert fibonacci
- 36. Analysis and Design of Algorithms Efficient algorithm
- 37. Analysis and Design of Algorithms Efficient algorithm short Time why????
- 38. Analysis and Design of Algorithms Fib_Fast algorithm is fast because of loop + array Time complexity = O(n2)
- 39. Analysis and Design of Algorithms Efficient algorithm Try Very long Time why????
- 40. Analysis and Design of Algorithms Advanced algorithm No array Need two variable + Loop
- 41. Analysis and Design of Algorithms Advanced algorithm Compute F6 a=0, b=1 0 1 a b
- 42. Analysis and Design of Algorithms Advanced algorithm Compute F6 a=b, b=a+b 1 1 a b
- 43. Analysis and Design of Algorithms Advanced algorithm Compute F6 a=b, b=a+b 1 2 a b
- 44. Analysis and Design of Algorithms Advanced algorithm Compute F6 a=b, b=a+b 2 3 a b
- 45. Analysis and Design of Algorithms Advanced algorithm Compute F6 a=b, b=a+b 3 5 a b
- 46. Analysis and Design of Algorithms Advanced algorithm Compute F6 a=b, b=a+b 5 8 a b
- 47. Analysis and Design of Algorithms Advanced algorithm Compute F6=8 5 8 a b
- 48. Analysis and Design of Algorithms Advanced algorithm
- 49. Analysis and Design of Algorithms Advanced algorithm Very short Time why????
- 50. Analysis and Design of Algorithms Fib_Faster algorithm is faster because of loop + two variables Time complexity = O(n)
- 51. Analysis and Design of Algorithms Advanced algorithm Try Short Time why????
- 52. Analysis and Design of Algorithms Greatest Common Divisors
- 53. Analysis and Design of Algorithms In mathematics, the greatest common divisor (gcd) of two or more integers, which are not all zero, is the largest positive integer that divides each of the integers.
- 54. Analysis and Design of Algorithms Input Integers a,b >=0 Output gcd(a,b)
- 55. Analysis and Design of Algorithms What is the greatest common divisor of 54 and 24? The divisors of 54 are: 1,2,3,6,9,18,27,54 Similarly, the divisors of 24 are: 1,2,3,4,6,8,12,24 The numbers that these two lists share in common are the common divisors of 54 and 24: 1,2,3,6 The greatest of these is 6. That is, the greatest common divisor of 54 and 24. gcd(54,24)=6
- 56. Analysis and Design of Algorithms Naive algorithm
- 57. Analysis and Design of Algorithms
- 58. Analysis and Design of Algorithms gcd algorithm is slow because of loop Time complexity = O(n) n depend on a,b
- 59. Analysis and Design of Algorithms Efficient algorithm
- 60. Analysis and Design of Algorithms Efficient algorithm
- 61. Analysis and Design of Algorithms Efficient algorithm gcd_fast((3918848, 1653264)) gcd_fast((1653264, 612320)) gcd_fast((612320, 428624)) gcd_fast((428624, 183696)) gcd_fast((183696, 61232)) return 61232
- 62. Analysis and Design of Algorithms Efficient algorithm Take 5 steps to solve gcd_fast( ( 3918848, 1653264 ) ) Time complexity = O(log(n)) n depend on a,b
- 63. Analysis and Design of Algorithms Naive algorithm is too slow. The Efficient algorithm is much better. Finding the correct algorithm requires knowing something interesting about the problem.
- 64. Analysis and Design of Algorithms facebook.com/mloey [email protected] twitter.com/mloey linkedin.com/in/mloey [email protected] mloey.github.io
- 65. Analysis and Design of Algorithms www.YourCompany.com © 2020 Companyname PowerPoint Business Theme. All Rights Reserved. THANKS FOR YOUR TIME
