Algorithms Lecture 7: Graph Algorithms

Analysis and Design of Algorithms
Graph Algorithms

Graph
Directed vs Undirected Graph
Acyclic vs Cyclic Graph
Backedge
Search vs Traversal
Breadth First Traversal
Depth First Traversal
Detect Cycle in a Directed Graph

 Graph data structure consists of a
finite set of vertices or nodes. The
interconnected objects are
represented by points termed as
vertices, and the links that connect
the vertices are called edges.
A
B C
D E
F
Node or Vertices
Edge

 Vertex: Each node of the graph is
represented as a vertex.
 V={A,B,C,D,E,F}
 Edge: Edge represents a path
between two vertices or a line
between two vertices.
 E={AB,AC,BD,BE,CE,DE,DF,EF}
A
B C
D E
F
Node or Vertices
Edge

A
B C
A
B C
Directed Graph Undirected Graph

A
B C
Acyclic Graph Cyclic Graph
A
B C

Backedge is an edge that is from node to itself
(selfloop), or one to its ancestor.
A
B
A

Search: Look for a given node
Traversal: Always visit all nodes

Breadth First Traversal

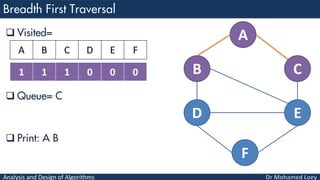
Breadth First Traversal (BFT) algorithm traverses all nodes
on graph in a breadthward motion and uses a queue to
remember to get the next vertex.

Layers A
B C
D E
F
Layer1
Layer2
Layer3
Layer4

 Visited=
 Queue=
 Print:
A
B C
D E
F
0 0 0 0 0 0
A B C D E F

 Visited=
 Queue=
 Print:
A
B C
D E
F
1 0 0 0 0 0
A B C D E F

 Visited=
 Queue= A
 Print:
A
B C
D E
F
1 0 0 0 0 0
A B C D E F

 Visited=
 Queue=
 Print: A
A
B C
D E
F
1 0 0 0 0 0
A B C D E F

 Visited=
 Queue=
 Print: A
A
B C
D E
F
1 1 1 0 0 0
A B C D E F

 Visited=
 Queue= B C
 Print: A
A
B C
D E
F
1 1 1 0 0 0
A B C D E F

 Visited=
 Queue= C
 Print: A B
A
B C
D E
F
1 1 1 0 0 0
A B C D E F

 Visited=
 Queue= C
 Print: A B
A
B C
D E
F
1 1 1 1 1 0
A B C D E F

 Visited=
 Queue= C D E
 Print: A B
A
B C
D E
F
1 1 1 1 1 0
A B C D E F

 Visited=
 Queue= D E
 Print: A B C
A
B C
D E
F
1 1 1 1 1 0
A B C D E F

 Visited=
 Queue= E
 Print: A B C
A
B C
D E
F
1 1 1 1 1 0
A B C D E F

 Visited=
 Queue= E
 Print: A B C D
A
B C
D E
F
1 1 1 1 1 0
A B C D E F

 Visited=
 Queue= E
 Print: A B C D
A
B C
D E
F
1 1 1 1 1 1
A B C D E F

 Visited=
 Queue= E F
 Print: A B C D
A
B C
D E
F
1 1 1 1 1 1
A B C D E F

 Visited=
 Queue= F
 Print: A B C D E
A
B C
D E
F
1 1 1 1 1 1
A B C D E F

 Visited=
 Queue=
 Print: A B C D E
A
B C
D E
F
1 1 1 1 1 1
A B C D E F

 Visited=
 Queue=
 Print: A B C D E F
A
B C
D E
F
1 1 1 1 1 1
A B C D E F

Breadth First on Tree

 V={0,1,2,3,4,5}
 E={01,02,13,14,24,34,35,45}
0
1 2
3 4
5

 Another Example:

Depth First Traversal

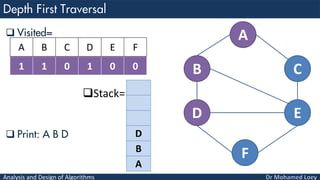
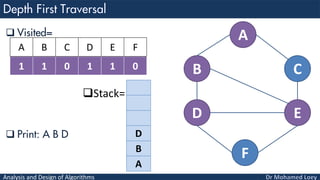
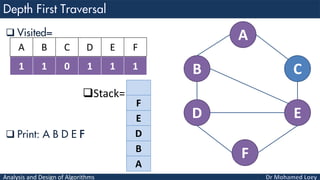
Depth First Traversal (DFT) algorithm traverses a graph in
a depthward motion and uses a stack to remember to get
the next vertex to start a search.

depthward motion A
B C
D E
F

 Visited=
Stack=
 Print:
A
B C
D E
F
0 0 0 0 0 0
A B C D E F

 Visited=
Stack=
 Print:
A
B C
D E
F
1 0 0 0 0 0
A B C D E F

 Visited=
Stack=
 Print:
A
B C
D E
F
1 0 0 0 0 0
A B C D E F
A

 Visited=
Stack=
 Print: A
A
B C
D E
F
1 0 0 0 0 0
A B C D E F
A

 Visited=
Stack=
 Print: A
A
B C
D E
F
1 1 0 0 0 0
A B C D E F
A

 Visited=
Stack=
 Print: A
A
B C
D E
F
1 1 0 0 0 0
A B C D E F
B
A

 Visited=
Stack=
 Print: A B
A
B C
D E
F
1 1 0 0 0 0
A B C D E F
B
A

 Visited=
Stack=
 Print: A B
A
B C
D E
F
1 1 0 1 0 0
A B C D E F
B
A

 Visited=
Stack=
 Print: A B
A
B C
D E
F
1 1 0 1 0 0
A B C D E F
D
B
A

 Visited=
Stack=
 Print: A B D
A
B C
D E
F
1 1 0 1 0 0
A B C D E F
D
B
A

 Visited=
Stack=
 Print: A B D
A
B C
D E
F
1 1 0 1 1 0
A B C D E F
D
B
A

 Visited=
Stack=
 Print: A B D
A
B C
D E
F
1 1 0 1 1 0
A B C D E F
E
D
B
A

 Visited=
Stack=
 Print: A B D E
A
B C
D E
F
1 1 0 1 1 0
A B C D E F
E
D
B
A

 Visited=
Stack=
 Print: A B D E
A
B C
D E
F
1 1 0 1 1 1
A B C D E F
E
D
B
A

 Visited=
Stack=
 Print: A B D E
A
B C
D E
F
1 1 0 1 1 1
A B C D E F
F
E
D
B
A

 Visited=
Stack=
 Print: A B D E F
A
B C
D E
F
1 1 0 1 1 1
A B C D E F
F
E
D
B
A

 Visited=
Stack=
A
B C
D E
F
1 1 0 1 1 1
A B C D E F
E
D
B
A

 Visited=
Stack=
A
B C
D E
F
1 1 1 1 1 1
A B C D E F
E
D
B
A

 Visited=
Stack=
 Print: A B D E F C
A
B C
D E
F
1 1 1 1 1 1
A B C D E F
C
E
D
B
A

 Visited=
Stack=
A
B C
D E
F
1 1 1 1 1 1
A B C D E F
E
D
B
A

 Visited=
Stack=
A
B C
D E
F
1 1 1 1 1 1
A B C D E F
D
B
A

 Visited=
Stack=
A
B C
D E
F
1 1 1 1 1 1
A B C D E F
B
A

 Visited=
Stack=
A
B C
D E
F
1 1 1 1 1 1
A B C D E F
A

 Visited=
Stack=
A
B C
D E
F
1 1 1 1 1 1
A B C D E F

Depth First on tree

Given a directed graph, check whether the graph
contains a cycle or not. Your function should return
true if the given graph contains at least one cycle,
else return false.

Depth First Traversal can be used to detect cycle in a
Graph. There is a cycle in a graph only if there is a
back edge present in the graph.

 Visited=
Stack=
A
C
B
D
0 0 0 0
A B C D

 Visited=
Stack=
A
C
B
D
1 0 0 0
A B C D

 Visited=
Stack=
A
C
B
D
1 0 0 0
A B C D
A

 Visited=
Stack=
A
C
B
D
1 1 0 0
A B C D
A

 Visited=
Stack=
A
C
B
D
1 1 0 0
A B C D
B
A

 Visited=
Stack=
A
C
B
D
1 1 1 0
A B C D
B
A

 Visited=
Stack=
A
C
B
D
1 1 1 0
A B C D
C
B
A

Graph contains cycle
A
C
B
D

facebook.com/mloey
mohamedloey@gmail.com
twitter.com/mloey
linkedin.com/in/mloey
mloey@fci.bu.edu.eg
mloey.github.io

Algorithms Lecture 7: Graph Algorithms

Recommended

More Related Content

What's hot (20)

Similar to Algorithms Lecture 7: Graph Algorithms (20)

More from Mohamed Loey (20)

Recently uploaded (20)

Algorithms Lecture 7: Graph Algorithms