An improved spfa algorithm for single source shortest path problem using forward star data structure
0 likes67 views
This document presents an enhanced Single-Source Shortest Path Faster Algorithm (SPFA) that utilizes a forward star data structure and the minpop principle to optimize queue operations, improving time efficiency for single-source shortest path problems in weighted graphs. The improved algorithm achieves an average time complexity of O(|e|), making it more effective compared to traditional SPFA algorithms, particularly for graphs with a large number of edges. Experimental results demonstrate its superiority in computational performance over existing methods, validating both its correctness and efficiency.
![International Journal of Managing Information Technology (IJMIT) Vol.6, No.1, February 2014
DOI : 10.5121/ijmit.2014.6102 15
AN IMPROVED SPFA ALGORITHM FOR SINGLE-
SOURCE SHORTEST PATH PROBLEM USING
FORWARD STAR DATA STRUCTURE
Xin Zhou
Department of Economic Engineering, Kyushu University,
Fukuoka 812-8581, Japan
ABSTRACT
We present an improved SPFA algorithm for the single source shortest path problem. For a random graph,
the empirical average time complexity is O(|E|), where |E| is the number of edges of the input network.
SPFA maintains a queue of candidate vertices and add a vertex to the queue only if that vertex is relaxed.
In the improved SPFA, MinPoP principle is employed to improve the quality of the queue. We theoretically
analyse the advantage of this new algorithm and experimentally demonstrate that the algorithm is efficient.
KEYWORDS
SPFA; single source; shortest path; queue; MinPoP principle
1. INTRODUCTION
The shortest path problem, which focuses on finding a shortest path from a source node to other
nodes, is a fundamental network optimization problem that has been applied in many domains
including transportation, routing, communications and management. It is also one of the most
fundamental operations on graphs. Recently, several types of shortest path problems have been
investigated. For instance, Ada Wai-Chee et al.[1] proposed an efficient index, namely, an
independent-set based labeling scheme for P2P distance querying; Takuya Akiba et al.[2]
presented a new method for shortest path distance queries, their method pre-computes distance
labels for vertices by performing a breadth-first search from every vertex; Andy Diwen Zhu et
al.[3] brought out Arterial Hierarchy(AH), an index structure that narrows the gap between theory
and practice in answering shortest path and distance queries on road network; an innovative
interactive method was proposed to address the Resource Constrained Shortest Path
Problem(RCSPP)[4];a set of novel techniques centered around Hub-accelerator framework were
introduced[5], which are used to compute the k-degree shortest path(finding the shortest path
between two vertices if their distance is within k).
The single-source shortest path problems have been studied intensively. DRAGAN VASILJEVIC
et al.[6] gave a novel linear algorithms for the single-source shortest path problem, the worse case
time complexity is
O(m + Clog C), where m is the number of edges and C is the ratio of the largest and the smallest
edge weight; Christine Rizkallah[7] put forward a formal proof that a well-known axiomatic
characterization of the single-source shortest path problem is correct.
In this paper, we propose a new algorithm for single-source shortest path distance queries. It is an
improvement of SPFA. It uses Forward Star data structure to store the edges, and employs](https://image.slidesharecdn.com/animprovedspfaalgorithmforsingle-sourceshortestpathproblemusingforwardstardatastructure-201015104006/85/An-improved-spfa-algorithm-for-single-source-shortest-path-problem-using-forward-star-data-structure-1-320.jpg)
![International Journal of Managing Information Technology (IJMIT) Vol.6, No.1, February 2014
16
MinPoP principle to optimize the doubly-linked queue. MinPoP, that is, finding the vertex with
the minimum distance to the source node and pop the vertex to the front of the queue.
The paper is organized as follows. Section 2 reviews SPFA algorithm and its SLF optimization
algorithm. Section 3 describes the improved SPFA algorithm. Section 4 is the experimental
analysis. Section 5 concludes this paper.
2. DESCRIPTION
Given a weighted directed graph G = (V, E) and a source vertex s, the SPFA algorithm finds the
shortest path from s to each vertex v in the graph. The length of the shortest path from s to v is
stored in d(v) for each vertex v.
Below is the description of SPFA algorithm[8]. Here Q is a first-in, first-out queue of candidate
vertices, and w(u, v) is the edge weight of (u, v).
Shortest-Path-Faster-Algorithm(G, s)
1 for each vertex v ≠s in V(G)
2 d(v) ← ∞
3 d(s) ← 0
4 push s into Q
5 while Q is not empty
6 u ← pop Q
7 for each edge (u, v) in E(G)
8 if d(u) + w(u, v) < d(v) then
9 d(v) ← d(u) + w(u, v)
10 if v is not in Q then
11 push v into Q
Small Label First (SLF) optimization. Instead of always pushing vertex v to the end of the queue,
we compare d(v) to d(front(Q)), and insert v to the front of the queue if d(v) is smaller. Here Q is
a doubly-linked queue of candidate vertices. The description of this technique is (after pushing v
to the end of the queue in line 11):
procedure Small-Label-First(G, Q)
if d(back(Q)) < d(front(Q)) then
u ← pop back of Q
push u into front of Q
Another optimization technique is Forward Star data structure which uses struct array to store
edges, edges starting from the same source node are linked in the array. The struct array is
constructed in the process of adding edges when reading in network data. The description of this
principle is:
procedure Initialization
…
foreach number i in array EH
i ← -1
…
…
procedure Addedge(a, b, w, tot, ET, EH)
the tot-th edge of array ET ← an edge with source node a, end node
b, weight w, pointer to next edge - the a-th number of array EH
the a-th number of array EH ← tot
tot ← tot+1
In the process of adding edge, tot is the current total number of edges, ET is a struct array, every
element of the array is an edge struct which includes the edge’s source node, the edge’s end node,](https://image.slidesharecdn.com/animprovedspfaalgorithmforsingle-sourceshortestpathproblemusingforwardstardatastructure-201015104006/85/An-improved-spfa-algorithm-for-single-source-shortest-path-problem-using-forward-star-data-structure-2-320.jpg)
![International Journal of Managing Information Technology (IJMIT) Vol.6, No.1, February 2014
21
In this paper, we propose an improved SPFA algorithm which has optimization innovation on
traditional SPFA algorithm. When the graph is large, the times of data movement will be less, and
the performance of algorithm will be better.
6. CONCLUSIONS
In this paper, we introduced an effective MinPoP-based SPFA algorithm for shortest path
distance computation in large graphs, both directed and undirected. There are two major ideas in
our approach. Firstly, we combine Forward Star data structure with optimization techniques. This
method is very efficient for SPFA. Secondly, for every loop of scanning the edges which start
from the same source node, we label the node with the minimum distance d, and move the node
into the front of Q after the loop. Experiments demonstrate our improved SPFA algorithm is a
correct and efficient algorithm.
ACKNOWLEDGEMENTS
This research is supported by China Scholarship Council’s State Scholarship Fund.
REFERENCES
[1] Ada Wai-Chee Fu, Huanhuan Wu, James Cheng, Shumo Chu, Raymond Chi-Wing Wong: IS-
LABEL: an Independent-Set based Labeling Scheme for Point-to-Point Distance Querying on Large
Graphs CoRR abs/1211.2367 (2012)
[2] Takuya Akiba, Yoichi Iwata, Yuichi Yoshida: Fast Exact Shortest-Path Distance Queries on Large
Networks by Pruned Landmark Labeling CoRR abs/1304.4661 (2013)
[3] Andy Diwen Zhu, Hui Ma, Xiaokui Xiao, Siqiang Luo, Youze Tang, Shuigeng Zhou: Shortest Path
and Distance Queries on Road Networks: Towards Bridging Theory and Practice CoRR
abs/1304.2576 (2013)
[4] Luigi Di Puglia Pugliese, Francesca Guerriero: A Reference Point Approach for the Resource
Constrained Shortest Path Problems. Transportation Science (TRANSCI) 47(2):247-265 (2013)
[5] Ruoming Jin, Ning Ruan, Bo You, Haixun Wang: Hub-Accelerator: Fast and Exact Shortest Path
Computation in Large Social Networks CoRR.abs/1305.0507 (2013)
[6] Dragan Vasiljevic, Milos Danilovic: A Novel Linear Algorithm for Shortest Paths in Networks.
APJOR 30(2) (2013)
[7] Christine Rizkallah: An Axiomatic Characterization of the Single-Source Shortest Path Problem.
Archive of Formal Proofs (AFP) 2013 (2013)
[8] Fanding Duan: A Faster Algorithm for Shortest Path-SPFA. Journal of Southwest Jiao Tong
University. 29(2):207-212 (1994)](https://image.slidesharecdn.com/animprovedspfaalgorithmforsingle-sourceshortestpathproblemusingforwardstardatastructure-201015104006/85/An-improved-spfa-algorithm-for-single-source-shortest-path-problem-using-forward-star-data-structure-7-320.jpg)
An improved spfa algorithm for single source shortest path problem using forward star data structure
- 1. International Journal of Managing Information Technology (IJMIT) Vol.6, No.1, February 2014 DOI : 10.5121/ijmit.2014.6102 15 AN IMPROVED SPFA ALGORITHM FOR SINGLE- SOURCE SHORTEST PATH PROBLEM USING FORWARD STAR DATA STRUCTURE Xin Zhou Department of Economic Engineering, Kyushu University, Fukuoka 812-8581, Japan ABSTRACT We present an improved SPFA algorithm for the single source shortest path problem. For a random graph, the empirical average time complexity is O(|E|), where |E| is the number of edges of the input network. SPFA maintains a queue of candidate vertices and add a vertex to the queue only if that vertex is relaxed. In the improved SPFA, MinPoP principle is employed to improve the quality of the queue. We theoretically analyse the advantage of this new algorithm and experimentally demonstrate that the algorithm is efficient. KEYWORDS SPFA; single source; shortest path; queue; MinPoP principle 1. INTRODUCTION The shortest path problem, which focuses on finding a shortest path from a source node to other nodes, is a fundamental network optimization problem that has been applied in many domains including transportation, routing, communications and management. It is also one of the most fundamental operations on graphs. Recently, several types of shortest path problems have been investigated. For instance, Ada Wai-Chee et al.[1] proposed an efficient index, namely, an independent-set based labeling scheme for P2P distance querying; Takuya Akiba et al.[2] presented a new method for shortest path distance queries, their method pre-computes distance labels for vertices by performing a breadth-first search from every vertex; Andy Diwen Zhu et al.[3] brought out Arterial Hierarchy(AH), an index structure that narrows the gap between theory and practice in answering shortest path and distance queries on road network; an innovative interactive method was proposed to address the Resource Constrained Shortest Path Problem(RCSPP)[4];a set of novel techniques centered around Hub-accelerator framework were introduced[5], which are used to compute the k-degree shortest path(finding the shortest path between two vertices if their distance is within k). The single-source shortest path problems have been studied intensively. DRAGAN VASILJEVIC et al.[6] gave a novel linear algorithms for the single-source shortest path problem, the worse case time complexity is O(m + Clog C), where m is the number of edges and C is the ratio of the largest and the smallest edge weight; Christine Rizkallah[7] put forward a formal proof that a well-known axiomatic characterization of the single-source shortest path problem is correct. In this paper, we propose a new algorithm for single-source shortest path distance queries. It is an improvement of SPFA. It uses Forward Star data structure to store the edges, and employs
- 2. International Journal of Managing Information Technology (IJMIT) Vol.6, No.1, February 2014 16 MinPoP principle to optimize the doubly-linked queue. MinPoP, that is, finding the vertex with the minimum distance to the source node and pop the vertex to the front of the queue. The paper is organized as follows. Section 2 reviews SPFA algorithm and its SLF optimization algorithm. Section 3 describes the improved SPFA algorithm. Section 4 is the experimental analysis. Section 5 concludes this paper. 2. DESCRIPTION Given a weighted directed graph G = (V, E) and a source vertex s, the SPFA algorithm finds the shortest path from s to each vertex v in the graph. The length of the shortest path from s to v is stored in d(v) for each vertex v. Below is the description of SPFA algorithm[8]. Here Q is a first-in, first-out queue of candidate vertices, and w(u, v) is the edge weight of (u, v). Shortest-Path-Faster-Algorithm(G, s) 1 for each vertex v ≠s in V(G) 2 d(v) ← ∞ 3 d(s) ← 0 4 push s into Q 5 while Q is not empty 6 u ← pop Q 7 for each edge (u, v) in E(G) 8 if d(u) + w(u, v) < d(v) then 9 d(v) ← d(u) + w(u, v) 10 if v is not in Q then 11 push v into Q Small Label First (SLF) optimization. Instead of always pushing vertex v to the end of the queue, we compare d(v) to d(front(Q)), and insert v to the front of the queue if d(v) is smaller. Here Q is a doubly-linked queue of candidate vertices. The description of this technique is (after pushing v to the end of the queue in line 11): procedure Small-Label-First(G, Q) if d(back(Q)) < d(front(Q)) then u ← pop back of Q push u into front of Q Another optimization technique is Forward Star data structure which uses struct array to store edges, edges starting from the same source node are linked in the array. The struct array is constructed in the process of adding edges when reading in network data. The description of this principle is: procedure Initialization … foreach number i in array EH i ← -1 … … procedure Addedge(a, b, w, tot, ET, EH) the tot-th edge of array ET ← an edge with source node a, end node b, weight w, pointer to next edge - the a-th number of array EH the a-th number of array EH ← tot tot ← tot+1 In the process of adding edge, tot is the current total number of edges, ET is a struct array, every element of the array is an edge struct which includes the edge’s source node, the edge’s end node,
- 3. International Journal of Managing Information Technology (IJMIT) Vol.6, No.1, February 2014 17 weight, and the pointer to next edge, the a-th number of EH is used to represent the pointer. EH is an integer array, in the initialization step, each number in EH is initialized to -1. -1 means the end of storage of edges which start from one specified source node. Compared to another vertex storage structure- adjacent table, forward star is more efficient for SPFA. 3. AN IMPROVED SPFA ALGORITHM We propose a MinPoP principle. From all the d (d is the distance from the single source node to the current node), we label the node with the minimum d and move it into front of Q. Here Q is a doubly-linked queue of candidate vertices. The description of the improved SPFA algorithm is: Improved-SPFA-Algorithm(G, s) 1 for each vertex v ≠s in V(G) 2 d(v) ← ∞ 3 d(s) ← 0 4 min ← ∞ 5 push s into front of Q 6 while Q is not empty 7 node p ← null 8 u ← pop Q 9 for each edge (u, v) in E(G) 10 if d(u) + w(u, v) < d(v) then 11 d(v) ← d(u) + w(u, v) 12 if v is not in Q then 13 push v into back of Q 14 if( d(v) < min ) then 15 min ← d(v) 16 label v as p 17 move p into front of Q The average time complexity of this algorithm is O(|E|), where |E| is the number of edges of the input network. When Forward Star data structure is used to store edges, for a specified source node s, all of its adjacent edges are added into the edge struct array ET one by one from the original network data, so if the weights of edges starting from s are in an ascending order, the improved algorithm is a little more efficient than SPFA and its SLF optimization algorithm. Because the weights of edges from s in ET are in a descending order, so the d(v) is in a decreasing trend, SLF needs to update the front of Q many times, however, MinPoP only updates the front of Q once. MinPoP and SLF have the similar strategy of selecting a priority node into the front of Q, SLF continually push new node v if d(v) < d(front(Q)), MinPoP labels the node with the minimum d, if d< min, move it into front of Q. 4. EXPERIMENTAL ANALYSIS We evaluate the performance of our method and compare with existing methods. All methods tested were programmed in C++ and compiled with the same compiler. All experiments were run on a computer with an Intel 2.16 GHz CPU, 888MB RAM, running Windows XP OS.
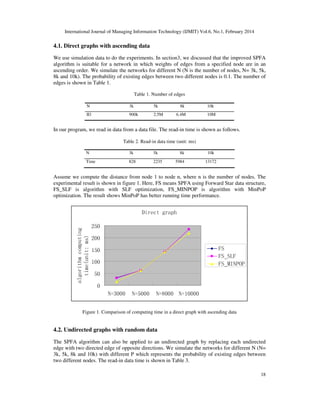
- 4. International Journal of Managing Information Technology (IJMIT) Vol.6, No.1, February 2014 18 4.1. Direct graphs with ascending data We use simulation data to do the experiments. In section3, we discussed that the improved SPFA algorithm is suitable for a network in which weights of edges from a specified node are in an ascending order. We simulate the networks for different N (N is the number of nodes, N= 3k, 5k, 8k and 10k). The probability of existing edges between two different nodes is 0.1. The number of edges is shown in Table 1. Table 1. Number of edges N 3k 5k 8k 10k |E| 900k 2.5M 6.4M 10M In our program, we read in data from a data file. The read-in time is shown as follows. Table 2. Read-in data time (unit: ms) N 3k 5k 8k 10k Time 828 2235 5984 13172 Assume we compute the distance from node 1 to node n, where n is the number of nodes. The experimental result is shown in figure 1. Here, FS means SPFA using Forward Star data structure, FS_SLF is algorithm with SLF optimization, FS_MINPOP is algorithm with MinPoP optimization. The result shows MinPoP has better running time performance. Direct graph 0 50 100 150 200 250 N=3000 N=5000 N=8000 N=10000 algorithm computing time(unit: ms) FS FS_SLF FS_MINPOP Figure 1. Comparison of computing time in a direct graph with ascending data 4.2. Undirected graphs with random data The SPFA algorithm can also be applied to an undirected graph by replacing each undirected edge with two directed edge of opposite directions. We simulate the networks for different N (N= 3k, 5k, 8k and 10k) with different P which represents the probability of existing edges between two different nodes. The read-in data time is shown in Table 3.
- 5. International Journal of Managing Information Technology (IJMIT) Vol.6, No.1, February 2014 19 Table 3. Read-in data time (unit: ms) P 0.1 0.2 0.3 N=3k 469 1015 1360 N=5k 1375 2578 4156 N=8k 3657 7703 10547 N=10k 9640 14234 15500 Assume we compute the distance from node 1 to node n, where n is the number of nodes. The experimental results are shown in figure 2-5. Undirect graph(N=3k) 0 50 100 150 200 250 0.1 0.2 0.3 edge existing probability algorithm computing time(unit:ms) FS FS_SLF FS_MINPOP Figure 2. Comparison of computing time in an undirected graph with N=3k Undiret graph(N=5k) 0 100 200 300 400 500 600 700 800 0.1 0.2 0.3 edge existing probability a lgori thm comp utin g tim e(un it:m s) FS FS_SLF FS_MINPOP Figure 3. Comparison of computing time in an undirected graph with N=5k
- 6. International Journal of Managing Information Technology (IJMIT) Vol.6, No.1, February 2014 20 Undirect graph(N=8k) 0 500 1000 1500 2000 2500 0.1 0.2 0.3 edge existing probability algorithm computing time(unit:ms) FS FS_SLF FS_MINPOP Figure 4. Comparison of computing time in an undirected graph with N=8k Undirect graph(N=10k) 0 500 1000 1500 2000 2500 3000 3500 4000 0.1 0.2 0.3 edge existing probability algorithm computing time(unit:ms) FS FS_SLF FS_MINPOP Figure 5. Comparison of computing time in an undirected graph with N=10k The results show that our improved SPFA algorithm can be applied to undirected graphs with comparative good running time performance. 5. COMPARISION The Shortest Path Faster Algorithm (SPFA) is an improvement of the Bellman–Ford algorithm which computes single-source shortest paths in a weighted graph. The algorithm is suitable for graphs that contain negative-weight edges, and it can work well on random sparse graphs. However, the worst-case complexity of SPFA is the same as that of Bellman–Ford, so for graphs with nonnegative edge weights, Dijkstra algorithm is preferred.
- 7. International Journal of Managing Information Technology (IJMIT) Vol.6, No.1, February 2014 21 In this paper, we propose an improved SPFA algorithm which has optimization innovation on traditional SPFA algorithm. When the graph is large, the times of data movement will be less, and the performance of algorithm will be better. 6. CONCLUSIONS In this paper, we introduced an effective MinPoP-based SPFA algorithm for shortest path distance computation in large graphs, both directed and undirected. There are two major ideas in our approach. Firstly, we combine Forward Star data structure with optimization techniques. This method is very efficient for SPFA. Secondly, for every loop of scanning the edges which start from the same source node, we label the node with the minimum distance d, and move the node into the front of Q after the loop. Experiments demonstrate our improved SPFA algorithm is a correct and efficient algorithm. ACKNOWLEDGEMENTS This research is supported by China Scholarship Council’s State Scholarship Fund. REFERENCES [1] Ada Wai-Chee Fu, Huanhuan Wu, James Cheng, Shumo Chu, Raymond Chi-Wing Wong: IS- LABEL: an Independent-Set based Labeling Scheme for Point-to-Point Distance Querying on Large Graphs CoRR abs/1211.2367 (2012) [2] Takuya Akiba, Yoichi Iwata, Yuichi Yoshida: Fast Exact Shortest-Path Distance Queries on Large Networks by Pruned Landmark Labeling CoRR abs/1304.4661 (2013) [3] Andy Diwen Zhu, Hui Ma, Xiaokui Xiao, Siqiang Luo, Youze Tang, Shuigeng Zhou: Shortest Path and Distance Queries on Road Networks: Towards Bridging Theory and Practice CoRR abs/1304.2576 (2013) [4] Luigi Di Puglia Pugliese, Francesca Guerriero: A Reference Point Approach for the Resource Constrained Shortest Path Problems. Transportation Science (TRANSCI) 47(2):247-265 (2013) [5] Ruoming Jin, Ning Ruan, Bo You, Haixun Wang: Hub-Accelerator: Fast and Exact Shortest Path Computation in Large Social Networks CoRR.abs/1305.0507 (2013) [6] Dragan Vasiljevic, Milos Danilovic: A Novel Linear Algorithm for Shortest Paths in Networks. APJOR 30(2) (2013) [7] Christine Rizkallah: An Axiomatic Characterization of the Single-Source Shortest Path Problem. Archive of Formal Proofs (AFP) 2013 (2013) [8] Fanding Duan: A Faster Algorithm for Shortest Path-SPFA. Journal of Southwest Jiao Tong University. 29(2):207-212 (1994)