Computer Graphics in Java and Scala - Part 1b

Computer Graphics
in Java and Scala
Part 1b
first see the Scala program translated into Java
then see the Scala program modified to produce a more intricate drawing
@philip_schwarz
slides by https://www.slideshare.net/pjschwarz

In this slide deck, which is an addendum to Part 1, we are going to do the following:
• Translate the Scala program from Part 1 into Java
• Modify the Scala program so that rather than drawing 50 concentric triangles, it draws a
chessboard-like grid in which each cell consists of 10 concentric squares.
• Eliminate an unsatisfactory feature of the above drawing by changing the angle by which
squares are twisted, plus improve the drawing by increasing the number of squares drawn.

case class Point(x: Float, y: Float)
object Triangle:
def apply(centre:Point,side:Float,height:Float): Triangle =
val Point(x,y) = centre
val halfSide = 0.5F * side
val bottomLeft = Point(x - halfSide, y - 0.5F * height)
val bottomRight = Point(x + halfSide, y - 0.5F * height)
val top = Point(x, y + 0.5F * height )
Triangle(bottomLeft,bottomRight,top)
case class Triangle(a: Point, b: Point, c: Point) public record Triangle(Point a, Point b, Point c) {
static Triangle instance(Point centre,Float side,Float height) {
float x = centre.x(), y = centre.y();
var halfSide = 0.5F * side;
var bottomLeft = new Point(x - halfSide, y - 0.5F * height);
var bottomRight = new Point(x + halfSide, y - 0.5F * height);
var top = new Point(x, y + 0.5F * height);
return new Triangle(bottomLeft,bottomRight,top);
}
}
public record Point(Float x, Float y) { }
Let’s start translating the
Scala program into Java.
@philip_schwarz

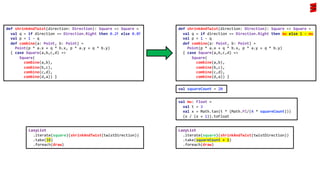
LazyList
.iterate(triangle)(shrinkAndTwist)
.take(50)
.foreach(draw)
Stream
.iterate(triangle, this::shrinkAndTwist)
.limit(50)
.forEach(t -> draw(g, t, panelHeight));

class TrianglesPanel extends JPanel:
setBackground(Color.white)
override def paintComponent(g: Graphics): Unit =
super.paintComponent(g)
val panelSize: Dimension = getSize()
val panelWidth = panelSize.width - 1
val panelHeight = panelSize.height - 1
val panelCentre = Point(panelWidth / 2, panelHeight / 2)
val triangleSide = 0.95F * Math.min(panelWidth, panelHeight)
val triangleHeight = (0.5F * triangleSide) * Math.sqrt(3).toFloat
…<shrinkAndTwist, draw and drawLine functions>…
val triangle = Triangle(panelCentre,
triangleSide,
triangleHeight)
LazyList
.take(50)
.foreach(draw)
public class TrianglesPanel extends JPanel {
public TrianglesPanel() {
setBackground(Color.white);
}
public void paintComponent(Graphics g){
super.paintComponent(g);
Dimension panelSize = getSize();
int panelWidth = panelSize.width - 1;
int panelHeight = panelSize.height - 1;
var panelCentre = new Point(panelWidth / 2F, panelHeight / 2F);
var triangleSide = 0.95F * Math.min(panelWidth, panelHeight);
var triangleHeight = (0.5F * triangleSide) * (float)Math.sqrt(3);
var triangle = Triangle.instance(panelCentre,
triangleSide,
triangleHeight);
Stream
.iterate(triangle, this::shrinkAndTwist)
.limit(50)
.forEach(t -> draw(g, t, panelHeight));
}
}

val shrinkAndTwist: Triangle => Triangle =
val q = 0.05F
val p = 1 - q
def combine(a: Point, b: Point) =
Point(p * a.x + q * b.x, p * a.y + q * b.y)
{ case Triangle(a,b,c) =>
Triangle(combine(a,b), combine(b,c), combine(c,a)) }
Triangle shrinkAndTwist(Triangle t) {
return new Triangle(
combine(t.a(), t.b()),
combine(t.b(), t.c()),
combine(t.c(), t.a())
);
}
Point combine(Point a, Point b) {
var q = 0.05F;
var p = 1 - q;
return new Point(p * a.x() + q * b.x(), p * a.y() + q * b.y());
}
val draw: Triangle => Unit =
case Triangle(a, b, c) =>
drawLine(a, b)
drawLine(b, c)
drawLine(c, a)
def drawLine(a: Point, b: Point): Unit =
val (ax,ay) = a.deviceCoords(panelHeight)
val (bx,by) = b.deviceCoords(panelHeight)
g.drawLine(ax, ay, bx, by)
void draw(Graphics g, Triangle t, int panelHeight) {
drawLine(g, t.a(), t.b(), panelHeight);
drawLine(g, t.b(), t.c(), panelHeight);
drawLine(g, t.c(), t.a(), panelHeight);
}
void drawLine(Graphics g, Point a, Point b, int panelHeight) {
var aCoords = deviceCoords(a, panelHeight);
var bCoords = deviceCoords(b, panelHeight);
int ax = aCoords.x, ay = aCoords.y, bx = bCoords.x, by = bCoords.y;
g.drawLine(ax, ay, bx, by);
}
java.awt.Point deviceCoords(Point p, int panelHeight) {
return new java.awt.Point(Math.round(p.x()), panelHeight - Math.round(p.y()));
}
extension (p: Point)
def deviceCoords(panelHeight: Int): (Int, Int) =
(Math.round(p.x), panelHeight - Math.round(p.y))

class Triangles:
JFrame.setDefaultLookAndFeelDecorated(true)
val frame =
new JFrame("Triangles: 50 triangles inside each other")
frame.setDefaultCloseOperation(WindowConstants.EXIT_ON_CLOSE)
frame.setSize(600, 400)
frame.add(TrianglesPanel())
frame.setVisible(true)
@main def main: Unit =
// Create a frame/panel on the event dispatching thread
SwingUtilities.invokeLater(
new Runnable():
def run: Unit = Triangles()
)
public class Triangles {
public static void main(String[] args) {
// Create a frame/panel on the event dispatching thread
() -> new Triangles().drawTriangles()
);
}
void drawTriangles() {
JFrame.setDefaultLookAndFeelDecorated(true);
var frame = new JFrame("Triangles: 50 triangles inside each other");
frame.setDefaultCloseOperation(WindowConstants.EXIT_ON_CLOSE);
frame.setSize(600, 400);
frame.add(new TrianglesPanel());
frame.setVisible(true);
}
}

On the next slide we check that the
Java program works as intended.

Computer Graphics in Java and Scala - Part 1b

Now we turn to an exercise that sees us modify the Scala program so that
rather than drawing 50 concentric triangles, it draws a chessboard-like
grid in which each cell consists of 10 concentric squares.

Exercises
…
1.2 Replace the triangles of program Triangles.java with squares and draw a great many of them, arranged in a
chessboard, as show in Fig 1.11.
As usual, this chessboard, consists of 𝑛 × 𝑛 normal squares (with horizontal and vertical edges), where 𝑛 = 8.
Each of these actually consists of 𝑘 squares of different sizes, with 𝑘 = 10.
Finally, the value 𝑞 = 0.2 (and 𝑝 = 1 − 𝑞 = 0.8) was used to divide each edge into two parts with ratio 𝑝 ∶ 𝑞 (see also
program Triangles.java of section 1.2), but the interesting pattern of Fig 1.11 was obtained by reversing the roles of
𝑝 and 𝑞 in half of the 𝑛 × 𝑛 ‘normal’ squares, which is similar to the black and white squares of a normal chessboard.
Your program should accept the values 𝑛, 𝑘 and 𝑞 as program arguments.
Figure 1.11 A chessboard of squares

On the next slide we start modifying the Scala program so that
it meets the new requirements (though we are not going to
bother getting the program to accept 𝑛, 𝑘 and 𝑞 as parameters).
@philip_schwarz

object Triangle:
def apply(centre: Point, side: Float, height: Float): Triangle =
val bottomLeft = Point(x - halfSide, y - 0.5F * height)
val bottomRight = Point(x + halfSide, y - 0.5F * height)
val top = Point(x, y + 0.5F * height )
Triangle(bottomLeft,bottomRight,top)
case class Triangle(a: Point, b: Point, c: Point) case class Square(a: Point, b: Point, c: Point, d: Point)
object Square:
def apply(centre: Point, side: Float): Square =
val bottomLeft = Point(x - halfSide, y - halfSide)
val bottomRight = Point(x + halfSide, y - halfSide)
val topRight = Point(x + halfSide, y + halfSide)
val topLeft = Point(x - halfSide, y + halfSide)
Square(bottomLeft,bottomRight,topRight,topLeft)

LazyList
.take(50)
.foreach(draw)
for
(row, startDirection) <- (0 until gridSize)
zip alternatingDirections(Direction.Right)
(col, twistDirection) <- (0 until gridSize)
zip alternatingDirections(startDirection)
square = Square(squareCentre(row,col),squareSide)
yield LazyList
.iterate(square)(shrinkAndTwist(twistDirection))
.take(10)
.foreach(draw)
def squareCentre(row: Int, col: Int): Point =
Point(panelCentre.x-(gridSize/2*squareSide)+(col*squareSide)+squareSide/2,
panelCentre.y-(gridSize/2*squareSide)+(row*squareSide)+squareSide/2)
enum Direction:
case Left, Right
def reversed: Direction = if this == Right then Left else Right
def alternatingDirections(startDirection: Direction): LazyList[Direction] =
LazyList.iterate(startDirection)(_.reversed)
We are going to use a for comprehension to work through each of the 64 cells in the 8 × 8 grid,
ensuring that each time we move from one cell to the next, we invert the direction (right = clockwise
and left = counterclockwise) in which we twist the concentric squares drawn within a cell.

object TrianglesPanel extends JPanel:
val triangleSide = 0.95F * Math.min(panelWidth, panelHeight)
val triangleHeight = (0.5F * triangleSide) * Math.sqrt(3).toFloat
val triangle = Triangle(panelCentre,
triangleSide,
triangleHeight)
LazyList
.take(50)
.foreach(draw)
object SquaresPanel extends JPanel:
val gridSize = 8
val squareSide: Float = 0.95F * Math.min(panelWidth, panelHeight) / gridSize
def squareCentre(row: Int, col: Int): Point =
Point(panelCentre.x-(gridSize/2*squareSide)+(col*squareSide)+squareSide/2,
panelCentre.y-(gridSize/2*squareSide)+(row*squareSide)+squareSide/2)
for
(row, startDirection) <- (0 until gridSize)
zip alternatingDirections(Direction.Right)
(col, twistDirection) <- (0 until gridSize)
zip alternatingDirections(startDirection)
square = Square(squareCentre(row,col),squareSide)
yield LazyList
.take(10)
.foreach(draw)

val shrinkAndTwist: Triangle => Triangle =
val q = 0.05F
val p = 1 - q
{ case Triangle(a,b,c) =>
Triangle(
combine(a,b),
combine(b,c),
combine(c,a)) }
val draw: Triangle => Unit =
case Triangle(a, b, c) =>
drawLine(a, b)
drawLine(b, c)
drawLine(c, a)
def shrinkAndTwist(direction: Direction): Square => Square =
val q = if direction == Direction.Right then 0.2F else 0.8F
val p = 1 - q
{ case Square(a,b,c,d) =>
Square(
combine(a,b),
combine(b,c),
combine(c,d),
combine(d,a)) }
val draw: Square => Unit =
case Square(a, b, c, d) =>
drawLine(a, b)
drawLine(b, c)
drawLine(c, d)
drawLine(d, a)

def drawTriangles: Unit =
val frame =
new JFrame("Triangles: 50 triangles inside each other")
frame.setDefaultCloseOperation(
WindowConstants.EXIT_ON_CLOSE)
frame.add(TrianglesPanel)
@main def trianglesMain: Unit =
// Create the frame/panel on the event dispatching thread
new Runnable():
def run: Unit = drawTriangles
)
def drawSquares: Unit =
val frame =
new JFrame("A chessboard of squares")
frame.setDefaultCloseOperation(
WindowConstants.EXIT_ON_CLOSE)
frame.add(SquaresPanel)
@main def squaresMain: Unit =
// Create the frame/panel on the event dispatching thread
new Runnable():
def run: Unit = drawSquares
)

On the next slide we have a go at
running the modified Scala program.

That’s nice, but it turns out that there is an unsatisfactory feature
in that drawing: we can improve the drawing by removing that
feature and increasing the number of squares drawn.
@philip_schwarz

This idea is further illustrated by drawing the pattern shown in figure 3.3a.
At first sight it looks complicated, but on closer inspection it is seen to be simply a square, outside a square,
outside a square etc.
The squares are getting successively smaller and they are rotating through a constant angle. In order to draw
the diagram, a technique is needed which, when given a general square, draws a smaller internal square
rotated through this fixed angle.
Suppose the general square has corners {(xi , yi) | i = 1, 2, 3, 4} and the i th side of the square is the line joining
(xi , yi) to (xi+1 , yi+1) - assuming additions of subscripts are modulo 4 - that is, 4 + 1 ≡ 1.
A general point on this side of the square, (x’i , y’i), is given by
((1 - 𝜇) × xi + 𝜇 × xi+1, (1 - 𝜇) × yi + 𝜇 × yi+1) where 0 ≤ 𝜇 ≤ 1

In fact 𝜇 : 1 - 𝜇 is the ratio in which the side is cut by this point. If 𝜇 is fixed and the four points {(xi , yi) | i = 1, 2,
3, 4} are calculated in the above manner, then the sides of the new square make an angle
𝛼 = tan-1[𝜇/(1 -𝜇)]
with the corresponding side of the outer square. So by keeping 𝜇 fixed for each new square, the angle between
consecutive squares remains constant at 𝛼. In figure 3.3a … there are 21 squares and 𝜇 = 0.1.
There is an unsatisfactory feature of the pattern in figure 3.3a: the inside of the pattern is 'untidy', the sides of
the innermost square being neither parallel to nor at 𝜋/4 radians to the corresponding side of the outermost
square.
This is corrected simply by changing the value of 𝜇 so as to produce the required relationship between the
innermost and outermost squares.
As was previously noted, with the calculation of each new inner square, the corresponding sides are rotated
through an angle of tan−1[𝜇/(1 −𝜇)] radians.
After 𝑛 + 1 squares are drawn, the inner square is rotated by 𝑛 × tan−1[𝜇/(1 −𝜇)] radians relative to the outer
square. For a satisfactory diagram this angle must be an integer multiple of 𝜋/4.
That is, 𝑛 × tan−1[𝜇/(1 −𝜇)] = t(𝜋/4) for some integer t, and hence
𝜇 =
tan[t(𝜋/4n)]
tan[t(𝜋/4n)]+1
To produce figure 3.3b, 𝑛 = 20 and t = 3 are chosen.

val mu: Float =
val t = 3
val x = Math.tan(t * (Math.PI/(4 * squareCount)))
(x / (x + 1)).toFloat
val q = if direction == Direction.Right then 0.2F else 0.8F
val p = 1 - q
Square(
combine(a,b),
combine(b,c),
combine(c,d),
combine(d,a)) }
val q = if direction == Direction.Right then mu else 1 - mu
val p = 1 - q
Square(
combine(a,b),
combine(b,c),
combine(c,d),
combine(d,a)) }
val squareCount = 20
LazyList
.take(10)
.foreach(draw)
LazyList
.take(squareCount + 1)
.foreach(draw)

Let’ run the improved
Scala program.

Before and after the improvements

That’s all. I hope
you enjoyed that.
@philip_schwarz

Computer Graphics in Java and Scala - Part 1b

More Related Content

What's hot (20)

Similar to Computer Graphics in Java and Scala - Part 1b (20)

More from Philip Schwarz (20)

Recently uploaded (20)

Computer Graphics in Java and Scala - Part 1b