Data Structures & Algorithms - Lecture 3

Data Structures and
Algorithms
By Mohamed Gamal
© Mohamed Gamal 2024
C++

The topics of today’s lecture:
Agenda

The List ADT
– A list is a sequence of elements, A0, A1, A2, … , An−1, with size n.
– An empty list has size 0.
– In a non-empty list, Ai follows A𝑖−1 𝑖 < 𝑛 and A𝑖−1 precedes A𝑖 (𝑖 > 0).
– The first element is A0, and the last is An−1.
– Elements are typically integers but can be of any type.
0 1 2 3 4 5 6
List

Operation Description
printList() Prints the list.
makeEmpty() Empties the list.
find(x) Returns the position of the first occurrence of x.
insert(x, i) Inserts x at position i.
remove(x) Removes the first occurrence of x.
findKth(i) Returns the element at position i.
next(i) Returns the position of the successor of the element at position i.
previous(i) Returns the position of the predecessor of the element at position i.

Implementation: Lists can be implemented using arrays, which can dynamically grow using a vector-like
approach to overcome fixed capacity limits.
Operations:
• printList: executes in linear time.
• findKth: executes in constant time.
• Insertion and Deletion: expensive if done at the front or middle, requiring O(n) time due to
shifting elements. In the worst case, inserting or deleting at the front requires shifting the entire
array – O(n).
• High End Operations: If operations occur at the end of the list, insertion and deletion are O(1).
Suitability:
• Suitable for lists with frequent high-end insertions and random access.
• Not suitable for lists with frequent insertions and deletions at the front or middle.
Alternative: Linked lists are a better option for frequent insertions and deletions throughout the list.
Simple Array Implementation of Lists

const int n = 7;
int arr[n] = { 1, 2, 3, 4, 5, 7, 7 };
1 2 3 4 5 6 7
0 1 2 3 4 5 6
List
const int n = 7;
int *arr = new int[n]; // allocate memory
for (int i = 0; i < n; i++)
arr[i] = i + 1;
delete[] arr; // free memory

#include <iostream>
using namespace std;
class ArrayList
{
private:
int *arr;
int capacity;
int size;
// Helper function to resize the array when needed
void resize()
{
capacity *= 2;
int *newArr = new int[capacity];
for (int i = 0; i < size; i++) {
newArr[i] = arr[i];
}
delete[] arr;
arr = newArr;
delete[] newArr;
}
public:
// Constructor
ArrayList(int cap = 10)
{
capacity = cap;
size = 0;
arr = new int[capacity];
}
// Destructor
~ArrayList() {
delete[] arr; // free memory
}
// Print the list
void printList() {
for (int i = 0; i < size; i++)
cout << arr[i] << " ";
cout << endl;
}
// Find the element at the kth position
int findKth(int k) {
if (k < 0 || k >= size) {
throw out_of_range("Index out of range");
}
return arr[k];
}
// Insert an element at the specified position
void insert(int element, int position) {
if (position < 0 || position > size) {
throw out_of_range("Index out of range");
}
if (size == capacity) { // If the array is full, resize it
resize();
}
// Shift elements to the right
for (int i = size; i > position; i--) {
arr[i] = arr[i - 1];
}
arr[position] = element;
size++;
}
// Check if the list is empty
bool isEmpty() {
return size == 0;
}
// Remove the first occurrence of the specified element
void remove(int element) {
int position = -1;
if (arr[i] == element) {
position = i;
break;
}
}
if (position == -1) {
cout << "Element not found" << endl;
return;
}
for (int i = position; i < size - 1; i++) {
arr[i] = arr[i + 1];
}
size--;
}
};
int main()
{
ArrayList list; // { 34, 12, 52, 16, 12, 7 }
list.insert(34, 0);
list.insert(12, 1);
list.insert(52, 2);
list.insert(16, 3);
list.insert(12, 4);
list.insert(7, 5);
cout << "List after insertion: ";
list.printList();
cout << "Element at position 2: " << list.findKth(2) << endl;
list.remove(52);
cout << "List after removing 52: ";
list.printList();
return 0;
}
Array List
C++
implementation

Linked Lists
– Linked Lists are used to create arrays of unknown (dynamic) size in memory.
– Linked lists can be maintained in sorted order by inserting or deleting an element at the proper
position in the list.
– To avoid the linear cost of insertion and deletion in arrays, linked lists are used.
– A linked list consists of nodes, each containing an element and a link (next pointer) to the next
node.
– The last node's next pointer is nullptr.
Head
Tail
NULL

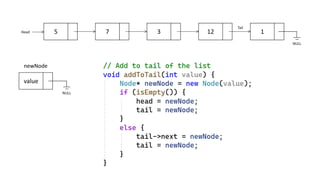
List initialize head and tail to Null (Constructor).
~List destroy all nodes of the list (destructor).
isEmpty determine whether or not the list is empty.
addToHead insert a new node at the front of the list.
addToTail insert a new node at the end of the list.
addNode insert a new node at a particular position.
findNode find a node with a given value.
DeleteNode delete a node with a given value.

deleteFromHead delete the first node from the list.
deleteFromTail delete the last node from the list.
printList print all the nodes in the list.
countList print the number of nodes in the list.

A Linked List:
Deletion from a linked list:
Insertion into a linked list:
Head
Tail
Head
Tail
Head
Tail

5 7 3 12 1
NULL
Tail
Head
value
NULL
newNode

5 7 3 12 1
NULL
Tail
Head
value
NULL
newNode
Position 1 Position 2 Position 3 Position 4 Position 5
Current

5 7 3 12 1
NULL
Tail
Head
Current
data next data next data next data next data next

5 7 3 12 1
NULL
Tail
Head
Temp

5 7 3 12 1
NULL
Tail
Head
Current
Tail
NULL

5 7 3 12 1
NULL
Tail
Head
Current
Tail
Previous
NULL
Current
Previous

#include <iostream>
// Node class for individual elements of the linked list
class Node {
public:
int data;
Node* next;
// Constructor (Ctor)
Node(int value) {
data = value;
next = nullptr;
}
};
// Linked list class
class LinkedList {
private:
Node* head;
Node* tail;
public:
// Constructor
LinkedList() {
head = nullptr;
tail = nullptr;
}
// Destructor
~LinkedList() {
Node* current = head;
while (current) {
Node* next = current->next;
delete current;
current = next;
}
head = nullptr;
tail = nullptr;
}
bool isEmpty() {
return head == nullptr;
}
// Add to the head of the list
void addToHead(int value) {
Node* newNode = new Node(value);
if (isEmpty()) {
head = newNode;
tail = newNode;
}
else {
newNode->next = head;
head = newNode;
}
}
// Add to tail of the list
void addToTail(int value) {
if (isEmpty()) {
head = newNode;
tail = newNode;
}
else {
tail->next = newNode;
tail = newNode;
}
}
// Add node at a specific position (1-based index)
void addNode(int value, int position) {
if (position <= 0) {
cerr << "Position must be positive." << endl;
return;
}
if (position == 1) {
addToHead(value);
}
else { // position 3
int currentPosition = 1;
while (currentPosition < position - 1 && current) {
current = current->next;
currentPosition++;
}
if (current) {
newNode->next = current->next;
current->next = newNode;
if (current == tail) {
tail = newNode;
}
}
else {
cerr << "Position exceeds the number of elements." << endl;
}
}
}
// Find node with a given value
Node* findNode(int value) {
while (current && current->data != value) {
}
return current;
}
// Delete node from head
void deleteFromHead() {
if (!isEmpty()) {
Node* temp = head;
head = head->next;
delete temp;
// If list is empty after deletion
if (!head) {
tail = nullptr;
}
}
else {
cerr << "List is empty." << endl;
}
}
// Delete node from tail
void deleteFromTail() {
if (!isEmpty()) {
// If only one node in the list
if (head == tail) {
delete head;
head = nullptr;
tail = nullptr;
}
else {
while (current->next != tail) {
}
delete tail;
tail = current;
tail->next = nullptr;
}
}
else {
}
}
// Delete node with a given value
void deleteNode(int value) {
Node* previous = nullptr;
previous = current;
}
if (current) {
if (current == head) {
deleteFromHead();
}
else if (current == tail) {
deleteFromTail();
}
else {
previous->next = current->next;
delete current;
}
}
else {
cerr << "Node with value " << value << " not found." << endl;
}
}
// Print all nodes in the list
void printList() {
while (current) {
cout << current->data << " ";
}
cout << endl;
}
// Count number of nodes in the list
int countList() {
int count = 0;
while (current) {
count++;
}
return count;
}
};
int main()
{
LinkedList myList;
myList.addToTail(10);
myList.addToHead(5);
cout << "List: ";
myList.printList();
cout << "Number of nodes: " << myList.countList() << endl;
myList.addNode(15, 3);
myList.deleteNode(20);
cout << "List after adding 15 at position 3 and deleting 20: ";
myList.printList();
cout << "Number of nodes after operations: " << myList.countList() << endl;
Node* foundNode = myList.findNode(10);
if (foundNode)
cout << "Node with value " << foundNode->data << " found." << endl;
else
cout << "Node with value 15 not found." << endl;
return 0;
}
Singly Linked List
C++
implementation

Variations of Linked Lists
1) Singly Linked List
– it’s difficult to go back and move through the list.
2) Doubly Linked List
– The list can be traversed in both directions, making sorting easier.
– Since the entire list can be accessed using either a forward link or a backward link, if one link fails, the list
can be rebuilt using the other link. This is particularly useful in case of equipment failure.
3) Circular Linked List
NULL A0 A1 A2 A3
NULL
Head
A0
Head A1 A2 A3
NULL
Tail
A0
Head A1 A2 A3
Tail

#include <iostream>
// Node class for individual elements of the doubly linked list
class Node
{
public:
int data;
Node* prev;
Node* next;
Node(int value) {
data = value;
prev = nullptr;
next = nullptr;
}
};
// Doubly linked list class
class DoublyLinkedList
{
private:
Node* head;
Node* tail;
public:
// Constructor
DoublyLinkedList() {
head = nullptr;
tail = nullptr;
}
// Destructor
~DoublyLinkedList() {
while (current) {
Node* next = current->next;
delete current;
current = next;
}
head = nullptr;
tail = nullptr;
}
bool isEmpty() {
}
// Add to head of the list
if (isEmpty()) {
head = newNode;
tail = newNode;
}
else {
head->prev = newNode;
head = newNode;
}
}
if (isEmpty()) {
head = newNode;
tail = newNode;
}
else {
newNode->prev = tail;
tail->next = newNode;
tail = newNode;
}
}
return;
}
if (position == 1) {
addToHead(value);
}
else {
while (currentPosition < position - 1 && current) {
currentPosition++;
}
if (current) {
newNode->prev = current;
if (current->next) {
current->next->prev = newNode;
}
if (current == tail) {
tail = newNode;
}
}
else {
cerr << "Position exceeds the number of elements." << endl;
}
}
}
// Find node with given value
}
return current;
}
// Delete node with given value
}
if (current) {
deleteFromHead();
}
else if (current == tail) {
deleteFromTail();
}
else {
current->prev->next = current->next;
if (current->next) {
current->next->prev = current->prev;
}
delete current;
}
}
else {
}
}
if (!isEmpty()) {
Node* temp = head;
head = head->next;
if (head) {
head->prev = nullptr;
}
else {
tail = nullptr;
}
delete temp;
}
else {
}
}
// Delete node from tail
void deleteFromTail() {
if (!isEmpty()) {
if (head == tail) {
delete head;
head = nullptr;
tail = nullptr;
}
else {
Node* temp = tail;
tail = tail->prev;
tail->next = nullptr;
delete temp;
}
}
else {
}
}
// Print all nodes in the list from head to tail
void printList() {
while (current) {
}
cout << endl;
}
// Print all nodes in the list from tail to head
void printListReverse() {
Node* current = tail;
while (current) {
current = current->prev;
}
cout << endl;
}
int countList() {
int count = 0;
while (current) {
count++;
}
return count;
}
};
int main()
{
DoublyLinkedList myList;
cout << "List (head to tail): ";
myList.printList();
cout << "List (tail to head): ";
myList.printListReverse();
myList.printList();
return 0;
}
Doubly Linked List
C++
implementation

#include <iostream>
// Node class for individual elements of the circular linked list
class Node
{
public:
int data;
Node* next;
Node(int value) {
data = value;
next = nullptr;
}
};
// Circular linked list class
class CircularLinkedList
{
private:
Node* head;
public:
// Constructor
CircularLinkedList() {
head = nullptr;
}
// Destructor
~CircularLinkedList() {
if (!isEmpty()) {
Node* current = head->next;
while (current != head) {
Node* temp = current;
delete temp;
}
delete head;
}
head = nullptr;
}
bool isEmpty() {
}
// Add to head of the list
if (isEmpty()) {
head = newNode;
head->next = head;
}
else {
Node* temp = head;
while (temp->next != head) {
temp = temp->next;
}
temp->next = newNode;
head = newNode;
}
}
if (isEmpty()) {
head = newNode;
head->next = head;
}
else {
Node* temp = head;
while (temp->next != head) {
temp = temp->next;
}
temp->next = newNode;
}
}
return;
}
if (position == 1 || isEmpty()) {
addToHead(value);
}
else {
while (currentPosition < position - 1 && current->next != head) {
currentPosition++;
}
}
}
// Find node with given value
if (isEmpty()) {
return nullptr;
}
do {
if (current->data == value) {
return current;
}
} while (current != head);
return nullptr;
}
// Delete node with given value
if (isEmpty()) {
return;
}
Node* previous = nullptr;
// Traverse until the node with the value is found or back to head
do {
if (current->data == value) {
break;
}
previous = current;
// If found, delete the node
// If head is the only node
if (current->next == head) {
delete head;
head = nullptr;
}
else {
// Move head to the next node and update the last node's next pointer
Node* last = head;
while (last->next != head) {
last = last->next;
}
last->next = head->next;
delete head;
head = last->next;
}
}
else if (current) {
// Delete the node and update the previous node's next pointer
previous->next = current->next;
delete current;
}
else {
}
}
if (!isEmpty()) {
Node* temp = head;
if (head->next == head) {
head = nullptr;
}
else {
Node* last = head;
while (last->next != head) {
last = last->next;
}
last->next = head->next;
head = head->next;
}
delete temp;
}
else {
}
}
// Print all nodes in the list
void printList() {
if (isEmpty()) {
cout << "List is empty." << endl;
return;
}
do {
cout << endl;
}
int countList() {
if (isEmpty()) {
return 0;
}
int count = 0;
do {
count++;
return count;
}
};
int main()
{
CircularLinkedList myList;
cout << "List: ";
myList.printList();
myList.printList();
return 0;
}
Circular Linked List
C++
implementation

Linked lists are more complex to code and manage than arrays, but they have some
distinct advantages.
• Dynamic: a linked list can easily grow and shrink in size.
• We don’t need to know how many nodes will be in the list. They are created in memory as needed.
• In contrast, the size of a C++ array is fixed at compilation time.
• Easy and fast insertions and deletions
• To insert or delete an element in an array, we need to copy to temporary variables to make room
for new elements or close the gap caused by deleted elements.
• With a linked list, no need to move other nodes. Only need to reset some pointers.
Array versus Linked Lists

Stack (LIFO)
– A stack is a linear data structure that can be accessed only at one of its ends for storing
and retrieving data.
– The stack is called a LIFO (last in, first out) structure.
– The last item in is the first one out of a stack.
2
4
1
3
6
Top
Push
Pop

clear Clear the stack.
isEmpty Check to see if the stack is empty.
push Put the element el on the top of the stack.
pop Takes the topmost element from the stack.
top Returns the topmost element in the stack without removing it.
size Returns the number of elements currently in the stack.
Stack
(LIFO)

Stack Applications
– The stack is a very frequently used ADT, in fact, most computer architectures implement a stack at the
very core of their instruction sets — both push and pop are assembly code instructions.
– Stack operations are very useful that there is a stack built into every program running on your PC — the
stack is a memory block that gets used to store the state of memory when a function is called, and to
restore it when a function returns (aka Call Stack).
– Converting and evaluating mathematical expressions (prefix, infix, postfix, …, etc.).
– Parsing syntax and checking for balanced symbols in compilers.
– Implementing undo/redo functionalities.
– Implementing back/forward navigation in web browsers.
– Expression Matching: Checking for balanced symbols in expressions (e.g., parentheses, brackets, …, etc.).

2 + 3 * 4 – 6 = 8
{ [ ( ) ] }

Stack Drawbacks
– No random access. You get the top, or nothing.
– No walking through the stack at all — you can only reach an element by popping all the
elements higher up off first
– No searching through a stack.

#include <iostream>
class Stack
{
private:
static const int MAX_SIZE = 100;
int arr[MAX_SIZE];
int topIndex;
public:
// Constructor
Stack() : topIndex(-1) {}
// Removes all elements from the stack
void clear() {
topIndex = -1;
}
// Checks if the stack is empty
bool isEmpty() const {
return topIndex == -1;
}
// Adds an element to the top of the stack
void push(int value) {
if (topIndex >= MAX_SIZE - 1)
throw overflow_error("Stack overflow");
arr[++topIndex] = value;
}
// Removes and returns the top element of the stack
int pop() {
if (isEmpty())
throw underflow_error("Stack underflow");
return arr[topIndex--];
}
// Returns the top element of the stack without removing it
int top() const {
if (isEmpty())
throw underflow_error("Stack is empty");
return arr[topIndex];
}
// Returns the number of elements in the stack
int size() const {
return topIndex + 1;
}
// Prints all elements of the stack
void printStack() const {
for (int i = topIndex; i >= 0; i--)
cout << arr[i] << endl;
cout << endl;
}
};
int main()
{
Stack stack;
stack.push(10);
stack.push(20);
stack.push(30);
cout << "Stack elements:" << endl;
stack.printStack(); // Should print 30, 20, 10
cout << "Top element: " << stack.top() << endl; // Should print 30
cout << "Stack size: " << stack.size() << endl; // Should print 3
cout << "Popped element: " << stack.pop() << endl; // Should print 30
cout << "Top element after pop: " << stack.top() << endl; // Should print 20
cout << "Stack size after pop: " << stack.size() << endl; // Should print 2
stack.clear();
cout << "Stack size after clear: " << stack.size() << endl; // Should print 0
cout << "Is stack empty: " << (stack.isEmpty() ? "Yes" : "No") << endl; // Should print Yes
return 0;
}
Stack (LIFO)
C++
implementation

Queues (FIFO)
– Just like the Stack ADT, a Queue is a linear data structure that is accessed in First-In, First-Out (FIFO)
order.
– Stack is a FIFO(First in First Out) data structure, which means that element inserted first will be
removed first, the second item put in is then removed, and so on.
– The process to add an element into queue is called Enqueue and the process of removal of an
element from queue is called Dequeue.
– A queue does not allow random access of any specific item.
– A linked list-based queue dynamically adjusts its size but comes with additional memory overhead for
storing pointers/references.

Queue Applications
– Queue, as the name suggests is used in everyday life whenever we need to manage any group of
objects in an order in which the first one coming in, also gets out first while the others wait for
their turn, like in the following scenarios:
• Ticket counter, lines at a bank or a fast-food restaurants.
• Serving requests on a single shared resource, like a printer, CPU task scheduling etc.
• Call Center phone systems uses Queues to hold people calling them in an order, until a service representative is
free.
– Used in many programming situations such as simulations, event or appointment scheduling (e.g.,
Gant chart), and I/O buffering.
– A whole branch of mathematics known as queuing theory deals with computing, probabilistically,
how long users expect to wait on a line, how long the line gets, and other such questions.

clear Clear the queue.
isEmpty Check to see if the queue is empty.
enqueue Put the element on the front of the queue.
dequeue Takes the front (first) element from the queue.
getFront Returns the topmost element in the queue without removing it.
size Returns the number of elements currently in the queue.
1 2 3 4 5 6 7
Front Rear
0 1 2 3 4 5 6

1 2 3 4 5 6
Front Rear
0 1 2 3 4 5 6

#include <iostream>
#include <stdexcept>
class LinearQueue
{
private:
static const int MAX_SIZE = 100; // Maximum size of the queue
int arr[MAX_SIZE]; // Array to store queue elements
int front; // Index of the front element
int rear; // Index of the rear element
int count; // Number of elements in the queue
public:
// Constructor
LinearQueue() : front(0), rear(-1), count(0) {}
// Clear the queue
void clear() {
front = 0;
rear = -1;
count = 0;
}
// Check to see if the queue is empty
return count == 0;
}
// Put the element on the front of the queue
void enqueue(int value) {
if (count == MAX_SIZE) {
throw overflow_error("Queue overflow");
}
rear = (rear + 1) % MAX_SIZE;
arr[rear] = value;
count++;
}
// Takes the front (first) element from the queue
int dequeue() {
if (isEmpty()) {
throw underflow_error("Queue underflow");
}
int value = arr[front];
front = (front + 1) % MAX_SIZE;
count--;
return value;
}
// Returns the topmost element in the queue without removing it
int getFront() const {
if (isEmpty()) {
throw underflow_error("Queue is empty");
}
return arr[front];
}
// Returns the number of elements currently in the queue
int size() const {
return count;
}
};
int main()
{
LinearQueue queue;
queue.enqueue(10);
queue.enqueue(20);
queue.enqueue(30);
cout << "Front element: " << queue.getFront() << endl; // Should print 10
cout << "Queue size: " << queue.size() << endl; // Should print 3
cout << "Dequeued element: " << queue.dequeue() << endl; // Should print 10
cout << "Front element after dequeue: " << queue.getFront() << endl; // Should print 20
cout << "Queue size after dequeue: " << queue.size() << endl; // Should print 2
queue.clear();
cout << "Queue size after clear: " << queue.size() << endl; // Should print 0
cout << "Is queue empty: " << (queue.isEmpty() ? "Yes" : "No") << endl; // Should print Yes
return 0;
}
Linear Queue
C++
implementation

Queues Variations
1) Linear Queue
– In a Linear queue, once the queue is completely full, it's not possible to insert more elements. Even if we dequeue the queue
to remove some of the elements, until the queue is reset, no new elements can be inserted.
2) Circular Queue
– In case of a circular queue, head pointer will always point to the front of the queue, and tail pointer
will always point to the end of the queue.
1 2 3 4 5 6 7
Front Rear

#include <iostream>
#include <stdexcept>
class CircularQueue
{
private:
static const int MAX_SIZE = 100; // Maximum size of the queue
int arr[MAX_SIZE]; // Array to store queue elements
int front; // Index of the front element
int rear; // Index of the rear element
int count; // Number of elements in the queue
public:
// Constructor
CircularQueue() : front(0), rear(0), count(0) {}
// Clear the queue
void clear() {
front = 0;
rear = 0;
count = 0;
}
// Check to see if the queue is empty
return count == 0;
}
// Put the element at the rear of the queue
void enqueue(int value) {
if (count == MAX_SIZE) {
throw overflow_error("Queue overflow");
}
arr[rear] = value;
rear = (rear + 1) % MAX_SIZE;
count++;
}
// Takes the front (first) element from the queue
int dequeue() {
if (isEmpty()) {
throw underflow_error("Queue underflow");
}
int value = arr[front];
front = (front + 1) % MAX_SIZE;
count--;
return value;
}
// Returns the front element in the queue without removing it
int getFront() const {
if (isEmpty()) {
throw underflow_error("Queue is empty");
}
return arr[front];
}
// Returns the number of elements currently in the queue
int size() const {
return count;
}
};
int main()
{
CircularQueue queue;
queue.enqueue(10);
queue.enqueue(20);
queue.enqueue(30);
cout << "Front element: " << queue.getFront() << endl; // Should print 10
cout << "Queue size: " << queue.size() << endl; // Should print 3
cout << "Dequeued element: " << queue.dequeue() << endl; // Should print 10
cout << "Front element after dequeue: " << queue.getFront() << endl; // Should print 20
cout << "Queue size after dequeue: " << queue.size() << endl; // Should print 2
queue.clear();
cout << "Queue size after clear: " << queue.size() << endl; // Should print 0
cout << "Is queue empty: " << (queue.isEmpty() ? "Yes" : "No") << endl; // Should print Yes
return 0;
}
Circular Queue
C++
implementation

Queue Drawbacks
– Fixed Size Limitation (Array-based Implementation)
• If a queue is implemented using a fixed-size array, there is a limitation on the number of elements it can
hold. This can lead to either unused space (if the array is too large) or overflow (if the array is too small).
– Memory Overhead (Linked List-based Implementation)
• A linked list-based queue dynamically adjusts its size but comes with additional memory overhead for
storing pointers/references. Each node requires extra space to store the pointer to the next node.
– Complexity in Circular Queue Implementation
• Implementing a circular queue can be more complex than a linear queue, as it requires handling wrap-
around logic for both the front and rear pointers.

Queue Drawbacks (Cont.)
– In a Linear queue, once the queue is completely full, it's not possible to insert more
elements. Even if we dequeue the queue to remove some of the elements, until the
queue is reset, no new elements can be inserted. Why?
• When we dequeue any element to remove it from the queue, we are actually moving the front of the
queue forward, thereby reducing the overall size of the queue. And we cannot insert new elements,
because the rear pointer is still at the end of the queue.
21 33 4 12 67 78 93
Front Rear
4 12 67 78 93
Front Rear
Queue
is full
Queue is full
(Even after removing )
2 elements

Basic Terminology – Map
– A map associates unique keys with values (i.e., <key, value> pairs).
Key Value
“Ahmed” $5000
“Mohamed” $4700
“Mona” $6100
“Gamal” $7000

#include <iostream>
#include <string>
template <typename K, typename V>
class Map {
private:
K* keys;
V* values;
int size;
int capacity;
void expand() {
capacity *= 2;
K* newKeys = new K[capacity];
V* newValues = new V[capacity];
newKeys[i] = keys[i];
newValues[i] = values[i];
}
delete[] keys;
delete[] values;
keys = newKeys;
values = newValues;
}
public:
Map() : size(0), capacity(10) {
keys = new K[capacity];
values = new V[capacity];
}
~Map() {
delete[] keys;
delete[] values;
}
void add(const K& key, const V& value) {
if (size == capacity)
expand();
keys[size] = key;
values[size] = value;
size++;
}
return size == 0;
}
V& operator[](const K& key) {
if (keys[i] == key)
return values[i];
// If key is not found, add it with a default value
expand();
keys[size] = key;
values[size] = V(); // Default value for type V
size++;
return values[size - 1];
}
void deleteKey(const K& key) {
if (keys[i] == key) {
for (int j = i; j < size - 1; j++) {
keys[j] = keys[j + 1];
values[j] = values[j + 1];
}
size--;
return;
}
}
}
void print() const {
cout << "<" << keys[i] << "," << values[i] << ">" << endl;
}
};
int main(void) {
Map<string, int> salaries;
salaries["Ahmed"] = 5000;
salaries["Mohamed"] = 4700;
salaries["Mona"] = 6100;
salaries["Gamal"] = 7000;
salaries.print();
return 0;
}
Map
C++
implementation
Method #1

#include <iostream>
#include <map>
#include <string>
int main() {
// map<key_type, value_type> map_name;
map<string, int> salaries = {
{"Ahmed", 5000},
{"Mohamed", 4700},
{"Mona", 6100},
{"Gamal", 7000}
};
// Add new element
salaries["Ali"] = 5500;
// Iterator to the first element
map<string, int>::iterator it = salaries.begin();
// Iterate over the map
while (it != salaries.end()) {
cout << "Key: " << it->first << ",t Value: " << it->second << endl;
it++;
}
return 0;
}
Map
C++
implementation
Method 2

Basic Terminology – Hashing
– A hash table uses a hash function to map general keys to corresponding indices in a table.
<key, value>
Key Value
“Ahmed” $5000
“Mohamed” $4700
“Mona” $6100
“Gamal” $7000
Hash
Function
𝝀
Hash
Value
Item
0
1
2 (Gamal, 5000)
3
4
5 (Mona, 5000)
6
7
8
9 (Ahmed, 5000)
hash value = sum ASCII codes % size
Size
=
10

Simple hash function
– You can use any other hashing function of your choice.
– In the previous slide we used a simple hash function as follows
Hash Value = Sum ASCII Codes % Size
– You can use any hash function of your choice, though.
Ahmed
A h m e d
65 104 109 101 100
Sum = 65 + 104 + 109 + 101 + 100 = 479
Hash Value = 479 % 10 = 9

#include <iostream>
#include <string>
int hashFunction(string name) {
int ascii_sum = 0;
for (int i = 0; i < name.size(); i++)
ascii_sum += int(name[i]);
return (ascii_sum % 10);
}
int main(void) {
string name = "Ahmed";
cout << "Hash value for " << name << " is " << hashFunction(name) << endl;
return 0;
}
Hash Function

class Hashing {
private:
Map<string, int> hashTable[10];
int ascii_sum = 0;
}
public:
void add(const string& key, const int& value) {
int hashValue = hashFunction(key);
hashTable[hashValue][key] = value;
}
int get(const string& key) {
return hashTable[hashValue][key];
}
void remove(const string& key) {
hashTable[hashValue].deleteKey(key);
}
void print() {
for (int i = 0; i < 10; i++) {
if (hashTable[i].isEmpty())
continue;
cout << "Hash value " << i << ": ";
hashTable[i].print();
}
}
};
Hashing Class
C++
implementation

#include <iostream>
#include <string>
template <typename K, typename V>
class Map {
private:
K* keys;
V* values;
int size;
int capacity;
void expand() {
capacity *= 2;
K* newKeys = new K[capacity];
V* newValues = new V[capacity];
newKeys[i] = keys[i];
newValues[i] = values[i];
}
delete[] keys;
delete[] values;
keys = newKeys;
values = newValues;
}
public:
Map() : size(0), capacity(10) {
keys = new K[capacity];
values = new V[capacity];
}
~Map() {
delete[] keys;
delete[] values;
}
void add(const K& key, const V& value) {
expand();
keys[size] = key;
values[size] = value;
size++;
}
return size == 0;
}
V& operator[](const K& key) {
if (keys[i] == key)
return values[i];
// If key is not found, add it with a default value
expand();
keys[size] = key;
values[size] = V(); // Default value for type V
size++;
return values[size - 1];
}
void deleteKey(const K& key) {
if (keys[i] == key) {
for (int j = i; j < size - 1; j++) {
keys[j] = keys[j + 1];
values[j] = values[j + 1];
}
size--;
return;
}
}
}
void print() const {
cout << "<" << keys[i] << "," << values[i] << ">" << endl;
}
};
class Hashing {
private:
Map<string, int> hashTable[10];
int ascii_sum = 0;
}
public:
void add(const string& key, const int& value) {
hashTable[hashValue][key] = value;
}
void remove(const string& key) {
hashTable[hashValue].deleteKey(key);
}
int get(const string& key) {
return hashTable[hashValue][key];
}
void print() {
for (int i = 0; i < 10; i++) {
if (hashTable[i].isEmpty())
continue;
cout << "Hash value " << i << ": ";
hashTable[i].print();
}
}
};
int main() {
Hashing hashing;
hashing.add("Ahmed", 5000);
hashing.add("Mohamed", 4700);
hashing.add("Mona", 6100);
hashing.add("Gamal", 7000);
hashing.print();
cout << "Ahmed's salary is " << hashing.get("Ahmed") << endl;
return 0;
}
All put together
C++
implementation

Collision Handling
– For two distinct keys k1 and k2, we may have the same hash value (i.e., h(k1) = h(k2)).
– We call this a collision.
– Collisions complicate our procedure of performing insertions, search and deletion
operations.
– There are multiple collision handling schemes, including separate chaining and linear
probing.
Separate chaining
Linear probing

Operation List
Hash Table
Expected Worst Case
Get item O(n) O(1) O(n)
Set item O(n) O(1) O(n)
Delete item O(n) O(1) O(n)
Length O(1) O(1) O(1)
Iterating O(n) O(n) O(n)
Hash Tables – Complexity

Trees – Basic Terminology
– A tree is an acyclic graph
– For our purposes, a tree is a collection of nodes (that can hold keys, data, …, etc.) that are connected by edges
– Trees are also oriented; each node has a parent and children.
– A node with no parents is the root of the tree, all child nodes are oriented downward.
– Nodes not immediately connected can have an ancestor, descendant or cousin relationship.
– A node with no children is called a leaf.
– A tree such that all nodes have at most two children is called a binary tree.
– A binary tree is also oriented horizontally: each node may have a left and/or a right
child.
– A binary tree is complete (also called full or perfect) if all nodes are present at
all levels, 0 up to its depth ‘d’.
– A path in a tree is a sequence nodes connected by edges.

Trees – Basic Terminology (Cont.)
– The length of a path in a tree is the number of edges in the path (which equals the number of nodes in the
path minus one).
– A path is simple if it does not traverse nodes more than once (this is the default type of path)
– The depth of a node ‘u’ is the length of the (unique) path from the root to ‘u’.
– The depth of the root is 0.
– The depth of a tree is the maximal depth of any node in the tree (sometimes the term height is used).
– All nodes of the same depth are considered to be at the same level.
– The height of a node u is the number of edges on the longest path from the
node ‘u’ to a leaf.

Depth of the whole tree is 3.
Tree height = 4
No. nodes = 16.
No. edges = No. nodes – 1 = 16 – 1 = 15
Lvl 0
Lvl 1
Lvl 2
Lvl 3
Root
Leaf Leaf
Leaf
Leaf
Leaf
Leaf
Leaf
Leaf
Leaf
Leaf
Node Height Depth
A 3 0
B 0 1
C 0 1
D 1 1
… … …

search Search for a particular element/key.
add
Adding an element
▪ Add at most shallow available spot.
▪ Add at a random leaf.
▪ Add internally, shift nodes down by some criteria.
remove
Removing an element
▪ Removing a leaf.
▪ Removing elements with one child.
▪ Removing elements with two children.
countNodes Compute the total number of nodes in the tree.
countLeaves Compute the total number of leaves in a tree.
findDepth Given a specific node, compute its depth.

Binary (search) Trees Properties
– In a binary tree, all nodes are connected by exactly one unique path.
– The maximum number of nodes at any level ‘k’ is 2𝑘
.
– The maximum number of nodes ‘n’ for any binary tree of
depth ‘d’ is
– The Binary Tree can be considered as a special form
of Linked List.
– A binary tree is considered balanced if, for every node in the tree, the height
difference between the left and right subtrees is at most one.
Binary Tree
Lvl 0
Lvl 1
Lvl 2
Lvl 3
Lvl 4
Lvl 5

Binary (search) Tree
– Each node has an associated key.
– For every node u with key uk in T
– Every node in the left-sub-tree of u has keys less than uk
– Every node in the right-sub-tree of u has keys greater than or equal to uk
– Duplicate keys can be handled, but you must be consistent and not guaranteed to be contiguous.
– Inductive property: all sub-trees are also binary search trees.
– In Sorted Binary Trees, elements on the right side of the root element are always greater than the
ones on the left.

Balanced vs. Unbalanced Binary Tree
1
2 3
4 5
df = 1
df = 0 df = 0
df = 0 df = 0
1
2 3
4 5
5
df = 2
df = 1 df = 0
df = 0 df = 1
df = 0
df = height of left child − height of right child
Balanced Unbalanced

Binary Tree – Representing Algebraic Expressions
a – b a – b/c a – b * c

Tree Traversal
– Level order traversal
– Pre-order traversal:
• Visits nodes in the following order: root; left-sub-tree; right-sub-tree.
– In-order traversal
• Visits nodes in the following order: left-sub-tree; root; right-sub-tree.
– Post-order traversal
• Visits nodes in the following order: left-sub-tree; right-sub-tree; root.

F
B G
A D
C E
I
H
Tree Traversal:
• Level Order (Breadth first)
• Depth-first
» Pre-order
» In-order (sorted)
» Post-order

F
B G
A D
C E
I
H
• Level Order: F,

F
B G
A D
C E
I
H
• Level Order: F, B

F
B G
A D
C E
I
H
• Level Order: F, B, G

F
B G
A D
C E
I
H
• Level Order: F, B, G, A

F
B G
A D
C E
I
H
• Level Order: F, B, G, A, D

F
B G
A D
C E
I
H
• Level Order: F, B, G, A, D, I

F
B G
A D
C E
I
H
• Level Order: F, B, G, A, D, I, C

F
B G
A D
C E
I
H
• Level Order: F, B, G, A, D, I, C, E

F
B G
A D
C E
I
H
• Level Order: F, B, G, A, D, I, C, E, H
DONE!

F
B G
A D
C E
I
H
• Pre-order: F

F
B G
A D
C E
I
H
• Pre-order: F, B

F
B G
A D
C E
I
H
• Pre-order: F, B, A

F
B G
A D
C E
I
H
• Pre-order: F, B, A, D

F
B G
A D
C E
I
H
• Pre-order: F, B, A, D, C

F
B G
A D
C E
I
H
• Pre-order: F, B, A, D, C, E

F
B G
A D
C E
I
H
• Pre-order: F, B, A, D, C, E, G

F
B G
A D
C E
I
H
• Pre-order: F, B, A, D, C, E, G, I

F
B G
A D
C E
I
H
• Pre-order: F, B, A, D, C, E, G, I, H
DONE!

F
B G
A D
C E
I
H
• In-order (sorted): A

F
B G
A D
C E
I
H
• In-order (sorted): A, B

F
B G
A D
C E
I
H
• In-order (sorted): A, B, C

F
B G
A D
C E
I
H
• In-order (sorted): A, B, C, D

F
B G
A D
C E
I
H
• In-order (sorted): A, B, C, D, E

F
B G
A D
C E
I
H
• In-order (sorted): A, B, C, D, E, F

F
B G
A D
C E
I
H
• In-order (sorted): A, B, C, D, E, F, G

F
B G
A D
C E
I
H
• In-order (sorted): A, B, C, D, E, F, G, H

F
B G
A D
C E
I
H
• In-order (sorted): A, B, C, D, E, F, G, H, I
DONE!

F
B G
A D
C E
I
H
• Post-order: A

F
B G
A D
C E
I
H
• Post-order: A, C

F
B G
A D
C E
I
H
• Post-order: A, C, E

F
B G
A D
C E
I
H
• Post-order: A, C, E, D

F
B G
A D
C E
I
H
• Post-order: A, C, E, D, B

F
B G
A D
C E
I
H
• Post-order: A, C, E, D, B, H

F
B G
A D
C E
I
H
• Post-order: A, C, E, D, B, H, I

F
B G
A D
C E
I
H
• Post-order: A, C, E, D, B, H, I, G

F
B G
A D
C E
I
H
• Post-order: A, C, E, D, B, H, I, G, F
DONE!

#include <iostream>
struct node
{
int data;
struct node* left;
struct node* right;
};
// New node creation
struct node* newNode(int data)
{
struct node* node = (struct node*) malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
// Pre-order Traversal
void traversePreOrder(struct node* temp)
{
if (temp != NULL) {
cout << " " << temp->data;
traversePreOrder(temp->left);
traversePreOrder(temp->right);
}
}
// In-order Traversal
void traverseInOrder(struct node* temp)
{
if (temp != NULL) {
traverseInOrder(temp->left);
traverseInOrder(temp->right);
}
}
// Post-order Traversal
void traversePostOrder(struct node* temp)
{
if (temp != NULL) {
traversePostOrder(temp->left);
traversePostOrder(temp->right);
}
}
int main()
{
struct node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
cout << "Pre-order traversal: ";
traversePreOrder(root);
cout << "nIn-order traversal: ";
traverseInOrder(root);
cout << "nPost-order traversal: ";
traversePostOrder(root);
}
Binary Tree
C++
implementation

Trees Applications
– File Systems where directories and files are organized in a hierarchical structure.
– Expression Parsing and Evaluation.
– Searching (Binary Search Trees (BST), AVL Trees, Red-Black Trees, …, etc.).
– Network Routing (Spanning Trees).
– Databases (B-trees, B+ trees, …, etc.) for database indexing.
– Artificial Intelligence (Decision Trees, Minimax Trees, …, etc.).

Dictionary of Algorithms and
Data Structures

Data Structures & Algorithms - Lecture 3

Recommended

More Related Content

Similar to Data Structures & Algorithms - Lecture 3 (20)

More from Faculty of Computers and Informatics, Suez Canal University, Ismailia, Egypt (20)

Recently uploaded (20)

Data Structures & Algorithms - Lecture 3