Design and Analysis of Algorithms Lecture Notes
- 1. DESIGN AND ANALYSIS OF ALGORITHMS Dr. C. Sreedhar Some of the contents of this presentation are copied from author Horowitz and from Internet
- 2. Algorithm • Algorithm was coined by Abu Ja'far Mohammed ibn Musa al Khowarizmi (825 AD). • An algorithm is composed of a finite set of steps, each of which may require one or more operations. • Where each operation must be definite, effective, terminate after finite number of operations. • An algorithm produces one or more outputs and may have zero or more inputs which are externally supplied.
- 4. Algorithm: Characteristics Algorithm Finiteness Definiteness Effectiveness Input Output clear and unambiguous well-defined termination condition basic, simple, and feasible operation zero or more inputs produces at least one output
- 5. Design and Analysis of Algorithms •Design: design algorithms which minimize the cost •Analysis: predict the cost of an algorithm in terms of resources and performance • Algorithm: An algorithm is a finite set of instructions that, if followed accomplishes a particular task
- 6. Study of Algorithms • How to devise an algorithm ? • How to express algorithm ? • How to validate algorithm ? • How to analyze algorithm ? • How to test a program ?
- 7. Space Complexity • A fixed part that is independent of the characteristics of the inputs and outputs. • Instruction space, space for simple variables and fixed-size component variables, space for constants. • A variable part that consists of the space needed by component variables whose size is dependent on the particular problem. • space needed by reference variables, recursion stack space
- 8. Space Complexity S(P) = C+Sp Where S(P): Space requirement C: fixed part Sp : instance characteristics ie., variable part
- 9. Space complexity: Example 1 • variables: a , b, c. • Single int variable uses 4 bytes so the total memory for this program is 12 bytes (3∗4 = 12 bytes). • The space complexity is of constant time, it can be expressed in big-O notation as O(1). Alorithm Sum { integer a,b,c Read a and b Compute c = a + b Display c }
- 10. Space complexity: Example 1 • variables: x , y, z, a , b. • Single variable uses 4 bytes so the total memory for this program is 20 bytes (5∗4=20 bytes). • The space complexity is of constant time, it can be expressed in big-O notation as O(1). Procedure Sum(a,b) return (a+b) End Sum Algorithm Add { integer x,y,z Display z= sum(x,y) }
- 11. Space complexity: Example 2 • Variables A[ ] is integer type with size n so its space complexity is 4∗n bytes. • Variables : n , i, arr_sum will take 4 bytes each, total 12 bytes ( 4∗3=12 bytes). • Total memory this program takes (4∗n+12) bytes. • The space complexity is increasing linearly with the size n, it can be expressed in big-O notation as O(n). Procedure sum(A,n) integer arr_sum arr_sum 0 for i 0 to n do arr_sum = arr_sum + A[i] repeat End sum
- 12. Time Complexity • tp : Run time of an algorithm • n : denotes the instance characteristics • ca, cs, cm, cd : time needed for an addition, subtraction, multiplication and division • ADD, SUB, MUL, DIV.. : functions
- 13. Algorithm: Sum of elements of array
- 15. Algorithm: Sum of two matrices
- 17. Asymptotic Notation • Mathematical notation used to describe the rate at which a function grows or decreases. • Used in analysis of algorithms to describe the time complexity and space complexity of an algorithm. • Helps to analyze the performance of an algorithm without having to run it on different inputs • Using asymptotic analysis, we can conclude the best case, average case, and worst case scenario of an algorithm
- 19. Asymptotic Notation • Big-O notation: – provides upper bound of a function. – represents worst-case scenario • Omega notation: – provides lower bound of a function. – represents best-case scenario • Theta notation: – Provides both an upper and lower bound – represents the average-case scenario
- 20. Big O notation f(n) = O(g(n)), iff positive constants c and n0, such that 0 f(n) cg(n), n n0
- 21. Big O notation: Example Consider f(n) = 3n+2 Can this function be represented as O(g(n)) ? f(n) = O(g(n)), iff positive constants c and n0, such that 0 f(n) cg(n), n n0 f(n) c*g(n) 3n+2 c*g(n) 3n+2 4*n for all n>=2 f(n) = O(g(n)) ie., 3n+2 = O(n), c=4 and n0 =2
- 22. Big O notation: Example 2 • f(n) = 3n2 + 2n + 4. • To find upper bound of f(n), we have to find c and n0 such that 0 ≤ f (n) ≤ c × g (n) for all n ≥ n0 • C=9 and n0 = 1 • 0 ≤ 3n2 +2n + 4 ≤ 9n2 • f(n) = O (g(n)) = O (n2) for c = 9, n0 = 1
- 23. Big O notation: Example 3 • Consider f(n) = 6 x 2n + n2 = O(2n), Find c and no • Solution • C=7 • no = 4
- 24. Big O notation (O) • Big O notation is helpful in finding the worst-case time complexity of a particular program. • Examples of Big O time complexity: • Linear search: O(N), where N is the number of elements in the given array • Binary search: O(Log N), where N is the number of elements in the given array • Bubble sort: O(n2), where N is the number of elements in the given array
- 25. Omega notation • Provides a lower bound on the growth rate of an algorithm’s running time or space usage. • It represents the best-case scenario, – i.e., the minimum amount of time or space an algorithm may need to solve a problem. • For example, if an algorithm’s running time is ?(n), then it means that the running time of the algorithm increases linearly with the input size n or more.
- 26. Omega notation f (n) = Ω(g(n)), iff positive constants c and n0, such that 0 ≤ c g(n) ≤ f (n), n n0
- 27. Omega notation: Example f (n) =3n+2 Can this function be represented as Ω (g(n)) ? f (n) = Ω(g(n)), iff positive constants c and n0, such that 0 ≤ c g(n) ≤ f (n), n n0 c*g(n) f(n); c= 3 and n0 = 1 3n 3n+2 f(n) = Ω (g(n)) = Ω (n) for c = 3, n0 = 1
- 28. Omega notation: Example f (n) =8n2+2n-3 Can this function be represented as Ω (g(n)) ? f (n) = Ω(g(n)), iff positive constants c and n0, such that 0 ≤ c g(n) ≤ f (n), n n0 c*g(n) f(n); c= 7 and n0 = 1 7*n2 8n2+2n-3 f(n) = Ω (g(n)) = Ω (n2) for c = 7, n0 = 1
- 29. Omega notation: Example f (n) = 2n3 + 4n + 5 Can this function be represented as Ω (g(n)) ? f (n) = Ω(g(n)), iff positive constants c and n0, such that 0 ≤ c g(n) ≤ f (n), n n0 Consider c= 2 and n0 = 1 0 ≤ 2n3 ≤ 2n3 + 4n + 5 f(n) = Ω (g(n)) = Ω (n3) for c = 2, n0 = 1
- 30. Theta notation • Provides both an upper and lower bound on the growth rate of an algorithm’s running time or space usage. • It represents the average-case scenario,
- 31. Theta notation f (n) = Θ(g(n)), iff positive constants c1, c2 and n0 ,such that 0 ≤ c1 *g(n) ≤ f(n) ≤ c2*g(n) n ≥ n0
- 32. Theta notation: Example f (n) = 4n+3 Can this function be represented as Θ (g(n)) ? f (n) = Θ(g(n)), iff positive constants c1, c2 and n0 ,such that 0 ≤ c1 *g(n) ≤ f(n) ≤ c2*g(n) n ≥ n0 Consider c1=4, c2=5 and n0 = 3 0 ≤ 4*3 ≤ 4(3)+3 ≤ 5*3 f(n) = Θ (g(n)) = Θ (n) for c1 = 4, c2 = 5, n0 = 1
- 33. Theta notation: Example • Consider f(n) = 3n+2. Represent f(n) in terms of Θ(n) and Find c1,c2 and n0 • Solution • C1= 3 • C2=4 • n0 = 2
- 34. Divide and Conquer Source: Internet
- 35. D & C: General method • Control abstraction for Divide and Conquer
- 37. Binary Search • Let ai, 1 ≤ i ≤ n be a list of elements which are sorted in nondecreasing order. • Determine whether a given element x is present in the list. • In case x is present, we are to determine a value j such that aj = x. • If x is not in the list then j is to be set to zero. • Can be solved using Iterative method or Recursive method
- 38. Binary Search Algorithm (Iterative)
- 39. Binary Search: Time complexity • Size of array = n • Iteration 1 - Length of array = n/2 • Iteration 2 - Length of array = (n/2)/2=n/22 • ……… • Iteration k - Length of array = n/2k • After k iterations, the size of the array becomes 1. • Length of array =n/ 2k =1 n = 2k • Applying log function on both sides: => log2(n)=log2(2k) => log2(n)=k∗log22=k => k=log2 (n)
- 40. Binary Search
- 41. Binary Search Algorithm (Recursive)
- 42. 1 BinSrch(a,1,7,10) BinSrch(a,5,7,10) 2 BinSrch(a,1,3,10) 2 BinSrch(a,7,7,10) BinSrch(a,5,5,10) 3 3 BinSrch(a,1,1,10) 3 BinSrch(a,3,3,10) 3 Binary Search: Recursive tree calls
- 43. 1 2 2 3 3 3 3 4 4 4 4 4 4 4
- 44. Finding Max and Min: D & C Straight Forward Approach
- 45. Finding Max and Min: Recursive
- 46. Finding Max and Min: Recursive calls of MaxMin Tree diagram
- 50. Merge Sort • Problem: elements in an array are to be sorted in non-decreasing order. • Given: A sequence of n elements • Output: Produce a single sorted sequence of n elements • Divide array into two halves, recursively sort left and right halves, then merge two.
- 51. Original 24 13 26 1 12 27 38 15 Divide in 2 24 13 26 1 12 27 38 15 Divide in 4 24 13 26 1 12 27 38 15 Divide in 8 24 13 26 1 12 27 38 15 Merge 2 13 24 1 26 12 27 15 38 Merge 4 1 13 24 26 12 15 27 38 Merge 8 1 12 13 15 24 26 27 38 Merge Sort
- 53. Algorithm Merge(lb,mid,ub) { b: Auxiliary Array i=lb; j=mid+1; k=lb; while(i<=mid AND j<=ub) { if(a[i]<a[j]) b[k++]=a[i++]; else b[k++]=a[j++]; } while(i<=mid) b[k++]=a[i++]; while(j<=ub) b[k++]=a[j++]; for(i=lb;i<=ub;i++) a[i]=b[i]; }
- 54. low high mid = 1 low high high high low low
- 55. low high mid = 1 low high high high low low
- 57. Time complexity of merge sort Best Case : O(n∗logn) Average Case: O(n∗logn) Worst Case : O(n∗logn)
- 58. Quick Sort • Problem: Sort the given elements using D & C • Divide: If set of elements contain two or more elements, choose the pivot element and divide accordingly. – Elements less than pivot – Element equals to pivot – Elements greater than pivot • Recursively sort • Conquer: Put elements back into order
- 59. Quick Sort • Pick one element in the array, which will be the pivot element • Make one pass through the array, called Partition step, rearrange such that – Entries smaller than pivot are to the left of the pivot – Entries larger than pivot are to the right • Recursively apply quick sort to the part of array that is to the left of the pivot and to the part on its right
- 60. Quick Sort Algorithm QuickSort (a,low,high) { } if (low < high) { } mid = partition(a, low, high); QuickSort(a, low, mid - 1); QuickSort(a, mid + 1, high);
- 61. Quick Sort Algorithm partition(a,low,high) { } pivot = a[high]; l = low; r = high - 1; while (l < r) { while (a[l] <= pivot && l < r) l++; while (a[r] >= pivot && l < r) r--; swap(a, l, r); } if(a[l] > a[high]) swap(a,l,high); else l = high; return l; Algorithm swap(a,i,j) { temp = a[i]; a[i] = a[j]; a[j] = temp; }
- 62. Quick Sort
- 63. Quick Sort: Best case
- 64. Quick Sort: Worst case
- 65. Finding Max and Min: D & C Straight Forward Approach Problem: Find the maximum and minimum items in a set of n elements Given: A list of elements stored in array Output: Maximum and minimum element in the array
- 66. Finding Max and Min: Recursive
- 67. Finding Max and Min: Recursive calls of MaxMin Tree diagram
- 71. Strassens Matrix Multiplication C11 = 1*5+2*7 = 19 C12 = 1*6+2*8 = 22 C21 = 3*5+4*7 = 43 C22 = 3*6+4*8 = 50 (1 + 4) * (5 + 8) = 65 (3 + 4) * 5 = 35 1 * (6 – 8) = -2 4 * (7 - 5) = 8 (1 + 2) * 8 = 24 (3 – 1) * (5 + 6) = 22 (2 – 4) * (7 + 8) = -30 (2 – 4) * (7 + 8) P + S – T + V = 19 R + T = 22 Q + S = 43 P + R – Q + U = 50
- 72. Greedy Method • The fundamental idea behind the greedy approach : – Build up the solution piece by piece – Make optimal choice locally on each piece – It may lead to global optimum solution. • Find a feasible solution that either maximizes of minimizes a given objective function. • Greedy method works in stages, considering one input at a time. • At each stage, a decision is made regarding whether a particular input is an optimal solution.
- 73. Greedy method: Control abstraction
- 74. Knapsack Problem
- 75. Greedy algorithm for knapsack Algorithm GreedyKnapsack(m,n) // p[i:n] and [1:n] contain the profits and weights respectively // if the n-objects ordered such that p[i]/w[i]>=p[i+1]/w[i+1], m size of knapsack and x[1:n] the solution vector { for i:=1 to n do x[i]:=0.0 U:=m; for i:=1 to n do { if(w[i]>U) then break; x[i]:=1.0; U:=U-w[i]; } if(i<=n) then x[i]:=U/w[i]; }
- 76. Algorithm GreedyKnapsack(m,n) { for i:=1 to n do x[i]:=0.0 U:=m; for i:=1 to n do { if(w[i]>U) then break; x[i]:=1.0; U:=U-w[i]; } if(i<=n) then x[i]:=U/w[i]; } X[1]=x[2]=x[3]=x[4]=x[5]=x[6]=0 n=6, p=(18, 5, 9, 10, 12, 7), w=(7, 2, 3, 5, 3, 2), M=13 U=13 i=1 3>13 false X[1]=1 U=13-3=10 i=2 2>10 false X[2]=1 U=10-2=8 i=3 3>8 false X[3]=1 U=8-3=5 i=4 7>5 True break X[4]= 5 ÷ 7 Profit = Profit (X1+X2+X3+(5/7)*X4) = 12+7+9+12.85 = 40.85
- 77. Job Sequencing with Deadlines • There is set of n-jobs. For any job i, is a integer deadling di≥0 and profit Pi>0, the profit Pi is earned iff the job completed by its deadline. • To complete a job one had to process the job on a machine for one unit of time. Only one machine is available for processing jobs. • A feasible solution for this problem is a subset J of jobs such that each job in this subset can be completed by its deadline.
- 78. • Obtain the optimal sequence for the following jobs. • n =4 j1 j2 j3 j4 • (P1, P2, P3, P4)= (100, 10, 15, 27) • (d1, d2, d3, d4)= (2, 1, 2, 1) Job Sequencing with Deadlines: Example
- 79. JSD: Algorithm • The value of a feasible solution J is the sum of the profits of the jobs in J, i.e., ∑i∈jPi • An optimal solution is a feasible solution with maximum value. //d dead line, jsubset of jobs ,n total number of jobs // d[i]≥1, 1 ≤ i ≤ n are the dead lines, // the jobs are ordered such that p[1]≥p[2]≥--- ≥p[n] • //j[i] is the ith job in the optimal solution 1 ≤ i ≤ k, k subset range
- 80. algorithm js(d, j, n) { d[0]=j[0]=0;j[1]=1;k=1; for i=2 to n do { r=k; while((d[j[r]]>d[i]) and [d[j[r]]≠r)) do r=r-1; if((d[j[r]]≤d[i]) and (d[i]> r)) then { for q:=k to (r+1) step-1 do j[q+1]= j[q]; j[r+1]=i; k=k+1; } } Job Sequencing with Deadlines: Algorithm
- 81. Let n =5; P = { 20, 15, 10, 5, 1 } and D = { 2, 2, 1, 3, 3 } d[0] = 0; j[0]= 0; j[1] = 1; k = 1 i=2 r=k=1 while(2>2 False if(2<=2 and (2>1) True { for(q=k;q>=r+1;q--) False j[2] = 2 k = 2 i=3 r=k=2 while( False if(2<=1 and (1>2) False i=4 r=k=2 while( False if(2<=3 and (3>2) True for(q=k;q>=r+1;q--) False j[3] = 4 k=3 i=5 r=k=3 while( False i=6 to 5 False Sequence of Jobs : (J1, J2, J4) Profit : p1+p2+p4 = 40 if(1<=3 and (3>3) False
- 83. Tree Vertex Splitting • Directed and weighted tree • Consider a network of power line transmission • The transmission of power from one node to the other results in some loss, such as drop in voltage • Each edge is labeled with the loss that occurs (edge weight) • N/w may not be able to tolerate losses beyond a certain level • You can place boosters in the nodes to account for the losses
- 84. Tree Vertex Splitting • Delay of tree T , d(T ) is maximum of all path delays • Splitting vertices to create forest • ∗ Let T /X be the forest that results when each vertex u ∈ X is split into two nodes ui and uo such that all the edges 〈u, j〉 ∈ E [〈j, u〉 ∈ E] are replaced by edges of the form 〈uo, j〉 ∈ E [〈j, ui〉 ∈ E] • Outbound edges from u now leave from uo • Inbound edges to u now enter at ui • ∗ Split node is the booster station
- 85. Tree Vertex Splitting • Tree vertex splitting problem is to identify a set X ⊆ V of minimum cardinality (minimum number of booster stations) for which d(T /X) ≤ δ for some specified tolerance limit δ – TVSP has a solution only if the maximum edge weight is ≤ δ • Given a weighted tree T = (V, E, w) and a tolerance limit δ, any X ⊆ V is a feasible solution if d(T /X) ≤ δ
- 86. Tree Vertex Splitting We want to minimize the number of booster stations (X) • For each node u ∈ V, compute maximum delay d(u) from u to any other node in its subtree • If v has a parent u such that d(v) + w(u, v) > δ, split v and set d(v) to zero • Computation proceeds from leaves to root • Delay for each leaf node is zero. • Let u be any node and C(u) be the set of all children of u. Then d(u) is given by: • If d(v) > δ, split v, set d(v) = 0
- 88. Tree Vertex Splitting Problem δ=5
- 89. Tree Vertex Splitting: Solution
- 93. MCST: Prim’s Algorithm • Step 1: • A vertex is chosen arbitrarily to serve as the initial vertex for the Minimum Spanning Tree. In general vertex a has been selected as the starting vertex.
- 94. MCST: Prim’s Algorithm • Find the smallest or lightest edge from a
- 95. MCST: Prim’s Algorithm • Find the smallest or lightest edge from b to neighboring vertices and a to c
- 96. MCST: Prim’s Algorithm • Find the smallest or lightest edge from b, d, and c
- 100. Solve MCST using Prim’s Algorithm
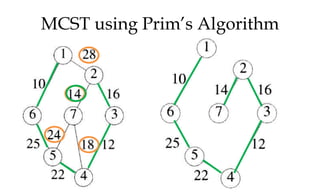
- 101. MCST using Prim’s Algorithm
- 102. MCST: Kruskal’s algorithm //E is the set of edges in G. ‘G’ has ‘n’ vertices //Cost {u,v} is the cost of edge (u,v) t is the set //of edges in the minimum cost spanning tree //The final cost is returned
- 103. MCST: Kruskals algorithm Algorithm Kruskal (E, cost, n,t) { construct a heap out of the edge costs using heapify; for i:= 1 to n do parent (i):= -1 i: = 0; min cost: = 0.0; While (i<n-1) and (heap not empty)) do { Delete a minimum cost edge (u,v) from the heaps; and reheapify using adjust; j:= find (u); k:=find (v); if (jk) then { i: = 1+1; t [i,1] = u; t [i,2] =v; mincost: =mincost+cost(u,v); Union (j,k); } } if (in-1) then write (“No spanning tree”); else return mincost; }
- 104. Optimal Storage on Tapes • There are n programs that are to be stored on a computer tape of length l. • Each program i is of length li 1 ≤ i ≤ n. • All the programs can be stored on the tape if and only if the sum of the lengths of the programs is at most L. • whenever a program is to be retrieved from this tape, the tape is initially positioned at the front
- 105. Optimal Storage on Tapes • tj : time needed to retrieve a program ij is proportional to • MRT: Mean Retrieval Time = • Find the permutation of n programs so that when the programs are stored in this order MRT is minimized
- 106. OST Example 1 • Let n = 3, (l1, l2, l3) = (5, 10, 3). Find optimal ordering? • Solution: • There are n! = 6 possible orderings.
- 107. OST Example 2 • Consider three programs (P1, P2, P3) with a length of (L1, L2, L3) = (5, 10, 2). Find optimal ordering?
- 108. Let n = 3, (l1, l2, l3) = (8, 12, 2)
- 109. Optimal Storage on Tapes l1 ≤l2 ≤l3 ≤…ln
- 110. OST Example 3 • Find an optimal placement for 13 programs on three tapes T0, T1 and T2, where the programs are of length 12, 5, 8, 32, 7, 5, 18,26, 4, 3, 11, 10, 6. • Solution: • According to algorithm, l1 ≤l2 ≤l3 ≤…ln • Programs: 3, 4, 5, 5, 6, 7, 8, 10,11, 12, 18, 26, 32 • Order : 1 2 3 4 5 6 7 8 9 10 11 12 13
- 111. n = no. of programs = 13 m = number of tapes = 3(T0,T1,T2) j = 0 i = 1 Write(“ap.”,1,tape,0) j = 1 mod 3 = 1 j = 1 i = 2 Write(“ap.”,2,tape,1) j = 2 mod 3 = 2 1 T0 2 T1 j = 2 i = 3 Write(“ap.”,3,tape,2) j = 3 mod 3 = 0 3 T2 j = 0 i = 4 Write(“ap.”,4,tape,0) j = 1 mod 3 = 1 4 T0 5 T1 6 T2 7 T0 8 T1 9 T2 10 T0 11 T1 12 T2 13 T0 1 4 7 10 13 Tape T0 Length 3 5 8 12 32 Tape T1 2 5 8 11 4 6 10 18 Tape T2 2 5 8 11 5 7 11 26
- 112. OST Example 4 • Find an optimal placement for 13 programs on three tapes T0, T1 and T2, where the programs are of length 12, 34, 56, 73, 24, 11, 34, 56, 78, 91, 34, 91, 45. • Solution:
- 113. Optimal Merge Patterns • Given n number of sorted files, the task is to find the minimum computations done to reach the optimal merge pattern. • Given n sorted files, there are many ways in which to pairwise merge them into a single sorted file. • The problem of OMP is that of determining an optimal way to pairwise merge n sorted files. • The two way merge pattern can be represented by binary merge trees.
- 115. In ascending order of lengths: 5, 10, 20, 30, 30
- 116. OMP: 4,5,7,8,10,12,20 4 5 9 7 8 15 10 19 12 27 20 39 66 L0 L1 L2 L3 L4 4*4+5*4+7*3+8*3+10*3+12*2+20*2 = 175
- 117. Single Source Shortest Path • In SSSP, given a directed graph G = (V,E), a weighting function cost for the edges of G and source vertex v. • The problem is to determine the shortest paths from v to all the remaining vertices of G. • It is assumed that all the weights are positive.
- 118. Single Source Shortest Path • Single source shortest path problem can be solved by either Dijikstra’s algorithm or Bellman Ford algorithm. • Dijkstra Algorithm is a graph algorithm for finding the shortest path from a source node to all other nodes in a graph. • Dijkstra algorithm is faster as compared to Bellman-Ford.
- 120. 2 1 3 4 5 i = 1 to 5 S[1] = false; dist[1]=cost[1,1] dist[1]=0 S[2] = false; dist[2]=cost[1,2] dist[2]=10 S[3] = false; dist[3]=cost[1,3] dist[3]=∞ S[4] = false; dist[4]=cost[1,4] dist[4]=5 S[5] = false; dist[5]=cost[1,5] dist[5]= ∞ S[1] = true; dist[1] = 0 dist[ 1] 0 0 0 0 dist[ 2] 10 8 8 8 dist[ 3] ∞ 14 13 9 dist[ 4] 5 5 5 5 dist[ 5] ∞ 7 7 7 S {1} {1,4} {1,4,5} {1,4,5,2} {1,4,5,2,3} dist[ 1] 0 dist[ 2] 8 dist[ 3] 9 dist[ 4] 5 dist[ 5] 7
- 121. Iteration S Vertex Selected 1 2 3 4 5 Initial - - 0 10 ∞ 5 ∞ 1 {1} 4 0 8 14 5 7 5 7 2 {1,4} 5 0 8 13 5 7 3 {1,4,5} 2 0 8 9 5 7 7 4 {1,4,5,2} 3 0 8 9 5 7 5 {1,4,5,2,3}
- 122. Single Source Shortest Path: Example











![Space complexity: Example 2
• Variables A[ ] is integer type with
size n so its space complexity is
4∗n bytes.
• Variables : n , i, arr_sum will take
4 bytes each, total 12 bytes
( 4∗3=12 bytes).
• Total memory this program
takes (4∗n+12) bytes.
• The space complexity is
increasing linearly with the size
n, it can be expressed in big-O
notation as O(n).
Procedure sum(A,n)
integer arr_sum
arr_sum 0
for i 0 to n do
arr_sum = arr_sum + A[i]
repeat
End sum](https://image.slidesharecdn.com/daapost-240405134921-2dcf40bc/85/Design-and-Analysis-of-Algorithms-Lecture-Notes-11-320.jpg)









































![Algorithm Merge(lb,mid,ub)
{
b: Auxiliary Array
i=lb;
j=mid+1;
k=lb;
while(i<=mid AND j<=ub)
{
if(a[i]<a[j]) b[k++]=a[i++];
else b[k++]=a[j++];
}
while(i<=mid) b[k++]=a[i++];
while(j<=ub) b[k++]=a[j++];
for(i=lb;i<=ub;i++) a[i]=b[i];
}](https://image.slidesharecdn.com/daapost-240405134921-2dcf40bc/85/Design-and-Analysis-of-Algorithms-Lecture-Notes-53-320.jpg)







![Quick Sort
Algorithm partition(a,low,high)
{
}
pivot = a[high]; l = low; r = high - 1;
while (l < r)
{
while (a[l] <= pivot && l < r) l++;
while (a[r] >= pivot && l < r) r--;
swap(a, l, r);
}
if(a[l] > a[high]) swap(a,l,high);
else l = high;
return l;
Algorithm swap(a,i,j)
{
temp = a[i];
a[i] = a[j];
a[j] = temp;
}](https://image.slidesharecdn.com/daapost-240405134921-2dcf40bc/85/Design-and-Analysis-of-Algorithms-Lecture-Notes-61-320.jpg)













![Greedy algorithm for knapsack
Algorithm GreedyKnapsack(m,n)
// p[i:n] and [1:n] contain the profits and weights respectively
// if the n-objects ordered such that p[i]/w[i]>=p[i+1]/w[i+1],
m size of knapsack and x[1:n] the solution vector
{
for i:=1 to n do x[i]:=0.0
U:=m;
for i:=1 to n do
{
if(w[i]>U) then break;
x[i]:=1.0;
U:=U-w[i];
}
if(i<=n) then x[i]:=U/w[i];
}](https://image.slidesharecdn.com/daapost-240405134921-2dcf40bc/85/Design-and-Analysis-of-Algorithms-Lecture-Notes-75-320.jpg)
![Algorithm GreedyKnapsack(m,n)
{
for i:=1 to n do x[i]:=0.0
U:=m;
for i:=1 to n do
{
if(w[i]>U) then break;
x[i]:=1.0;
U:=U-w[i];
}
if(i<=n) then x[i]:=U/w[i];
}
X[1]=x[2]=x[3]=x[4]=x[5]=x[6]=0
n=6, p=(18, 5, 9, 10, 12, 7), w=(7, 2, 3, 5, 3, 2), M=13
U=13
i=1
3>13 false
X[1]=1
U=13-3=10
i=2
2>10 false
X[2]=1
U=10-2=8
i=3
3>8 false
X[3]=1
U=8-3=5
i=4
7>5 True
break
X[4]= 5 ÷ 7
Profit = Profit (X1+X2+X3+(5/7)*X4) = 12+7+9+12.85 = 40.85](https://image.slidesharecdn.com/daapost-240405134921-2dcf40bc/85/Design-and-Analysis-of-Algorithms-Lecture-Notes-76-320.jpg)


![JSD: Algorithm
• The value of a feasible solution J is the sum of the profits of
the jobs in J, i.e., ∑i∈jPi
• An optimal solution is a feasible solution with maximum
value.
//d dead line, jsubset of jobs ,n total
number of jobs
// d[i]≥1, 1 ≤ i ≤ n are the dead lines,
// the jobs are ordered such that p[1]≥p[2]≥---
≥p[n]
• //j[i] is the ith job in the optimal solution
1 ≤ i ≤ k, k subset range](https://image.slidesharecdn.com/daapost-240405134921-2dcf40bc/85/Design-and-Analysis-of-Algorithms-Lecture-Notes-79-320.jpg)
![algorithm js(d, j, n)
{
d[0]=j[0]=0;j[1]=1;k=1;
for i=2 to n do {
r=k;
while((d[j[r]]>d[i]) and [d[j[r]]≠r)) do
r=r-1;
if((d[j[r]]≤d[i]) and (d[i]> r)) then
{
for q:=k to (r+1) step-1 do j[q+1]= j[q];
j[r+1]=i;
k=k+1;
}
}
Job Sequencing with
Deadlines: Algorithm](https://image.slidesharecdn.com/daapost-240405134921-2dcf40bc/85/Design-and-Analysis-of-Algorithms-Lecture-Notes-80-320.jpg)
![Let n =5; P = { 20, 15, 10, 5, 1 } and D = { 2, 2, 1, 3, 3 }
d[0] = 0; j[0]= 0;
j[1] = 1; k = 1
i=2
r=k=1
while(2>2 False
if(2<=2 and (2>1) True
{
for(q=k;q>=r+1;q--) False
j[2] = 2
k = 2
i=3
r=k=2
while( False
if(2<=1 and (1>2) False
i=4
r=k=2
while( False
if(2<=3 and (3>2) True
for(q=k;q>=r+1;q--) False
j[3] = 4
k=3
i=5
r=k=3
while( False
i=6 to 5 False
Sequence of Jobs : (J1, J2, J4)
Profit : p1+p2+p4 = 40
if(1<=3 and (3>3) False](https://image.slidesharecdn.com/daapost-240405134921-2dcf40bc/85/Design-and-Analysis-of-Algorithms-Lecture-Notes-81-320.jpg)


![Tree Vertex Splitting
• Delay of tree T , d(T ) is maximum of all path delays
• Splitting vertices to create forest
• ∗ Let T /X be the forest that results when each vertex
u ∈ X is split into two nodes ui and uo such that all
the edges 〈u, j〉 ∈ E [〈j, u〉 ∈ E] are replaced by
edges of the form 〈uo, j〉 ∈ E [〈j, ui〉 ∈ E]
• Outbound edges from u now leave from uo
• Inbound edges to u now enter at ui
• ∗ Split node is the booster station](https://image.slidesharecdn.com/daapost-240405134921-2dcf40bc/85/Design-and-Analysis-of-Algorithms-Lecture-Notes-84-320.jpg)

















![MCST: Kruskals algorithm
Algorithm Kruskal (E, cost, n,t)
{
construct a heap out of the edge costs using heapify;
for i:= 1 to n do parent (i):= -1
i: = 0; min cost: = 0.0;
While (i<n-1) and (heap not empty)) do
{
Delete a minimum cost edge (u,v) from the heaps; and reheapify using adjust;
j:= find (u); k:=find (v);
if (jk) then
{ i: = 1+1; t [i,1] = u; t [i,2] =v; mincost: =mincost+cost(u,v); Union (j,k); }
}
if (in-1) then write (“No spanning tree”); else return mincost;
}](https://image.slidesharecdn.com/daapost-240405134921-2dcf40bc/85/Design-and-Analysis-of-Algorithms-Lecture-Notes-103-320.jpg)
















![2
1
3
4 5
i = 1 to 5
S[1] = false; dist[1]=cost[1,1] dist[1]=0
S[2] = false; dist[2]=cost[1,2] dist[2]=10
S[3] = false; dist[3]=cost[1,3] dist[3]=∞
S[4] = false; dist[4]=cost[1,4] dist[4]=5
S[5] = false; dist[5]=cost[1,5] dist[5]= ∞
S[1] = true; dist[1] = 0
dist[ 1] 0 0 0 0
dist[ 2] 10 8 8 8
dist[ 3] ∞ 14 13 9
dist[ 4] 5 5 5 5
dist[ 5] ∞ 7 7 7
S
{1}
{1,4}
{1,4,5}
{1,4,5,2}
{1,4,5,2,3}
dist[ 1] 0
dist[ 2] 8
dist[ 3] 9
dist[ 4] 5
dist[ 5] 7](https://image.slidesharecdn.com/daapost-240405134921-2dcf40bc/85/Design-and-Analysis-of-Algorithms-Lecture-Notes-120-320.jpg)

