DSA (Data Structure and Algorithm) Questions

1. Given the following sequence of letters and asterisks: EAS*Y*QUE***ST***IO*N***
(a) Consider the stack data structure, supporting two operations push and pop, as discussed in
class. Suppose that for the above sequence, each letter (such as E) corresponds to a push of that
letter onto the stack and each asterisk (*) corresponds to a pop operation on the stack. Show the
sequence of values returned by the pop operations.
(b) Consider the queue data structure, supporting two operations insert and remove, as discussed
in class. Suppose that for the above sequence, each letter (such as E) corresponds to an insert of
that letter into the queue and each asterisk (*) corresponds to a remove operation on the queue.
Show the sequence of values returned by the remove operations.
Answer:
a).answer for stack Output: SYEUQTSAONIE.
b).answer for Queue Output: EASYQUESTION
2.Suppose you were asked to write a method that will take two sorted stacks A and B (min on top)
and create one stack that is sorted (min on top). You are allowed to use only the stack operations
such as pop, push, size and top. No other data structure such as arrays are not allowed. You are
allowed to use stacks. Note that elements on the stack can be compared using compareTo.
Public Stack mergeSortedStacks(Stack A, Stack B)
{
…...
}
Answer:
3. Evaluate the postfix expression: 10 5 + 60 6 / * 8 -

Answer :142
4.Write a recursive delete method for singly-linked lists with integer data that deletes the
first occurrence of a given integer from the list and returns the resulting list.
class ListNode
{
private int value; //data value
Public ListNode next; //next element of list, or null if last
public ListNode(int v)
{
value = v;
}
public int value()
{
return value;
}
}
Answer :
static ListNode delete(int i, ListNode s)
{
if (s == null)
return s;
if (s.value() == i)
return s.next;
s.next = delete(i, s.next);
return s;
}
5.If the sequence of operations - push (1), push (2), pop, push (1), push (2), pop, pop, pop, push
(2), pop are performed on a stack, then what will be the sequence of popped out values?
Answer:
Qusetion 6 :-Suppose you want to get from s to t on weighted graph G with
nonnegative edge weights, but you would like to stop by u if it isn’t too
inconvenient. (Here too inconvenient means that it increases the length of

your travel by more than 10%.) Describe an efficient algorithm that would
determine an optimal s to t path given your preference for stopping at u along
the way if not too inconvenient. It should either return the shortest path from s
to t, or the shortest path from s to t containing u.
Solution: Run Dijkstra’s algorithm twice, once from s and once from u. The
shortest path from s to t containing u is composed of the shortest path from s
to u and the shortest path from u to t. Compare the length of this path with the
length of the path from s to t, and choose the one to return based on their
lengths.
Question 7 :- Construct a Binary Tree From Inorder and Preorder Traversal
Inorder Traversal: {4,2,17,5,8,3,6}
Preorder Traversal :{1,2,4,3,5,7,8,6}
Answer:
Question 8 :- Write a recursive solution to Check whether a binary tree is a
complete tree or not.
Hint:(A complete binary tree is a binary tree whose all levels except the last
level are completely filled and all the leaves in the last level are all to the left
side.)

Solution:

https://www.geeksforgeeks.org/check-whether-binary-tree-complete-not-set-
2-recursive-solution/
Question 9:-List the nodes of the tree below in preorder, postorder, and breadth-first
order
Answer :-
Preorder: L,K,A,J,B,C,I,H,E,D,F,G
Postorder: A,B,C,J,K,I,D,E,F,G,H,L.
Breadth-first: L,K,I,H,A,J,E,F,G,B,C,D
Question 10 :-In the binary search tree below, carry out the following operations in
sequence: Add 5, add 17, delete 23, delete 9.
Answer: There is more than one way to do the deletes, so the final answer is not
unique, but here is one:

Question 11:-T is a min heap of height 3. What is the largest number of nodes that
Tcan have? What is the smallest number?
Answer:The first three levels (including the root) must be fully filled out, giving a
total of 7 nodes. The 4th level has between 1 node and 8 nodes. So the total number
of nodes in the heap is between 8 and 15.
Question 12 : For each of the directed graphs shown below:
If it is acyclic, give a topological sort.
If it is not acyclic, find a cycle.

Answer: Graph 1: Acyclic. Topological sort: A, B, D, C.
Graph 2: Cyclic. Cycle: F,H,G,F
Graph 3: Acyclic. There are several different topological sorts. I,J,K,L,M is one.
Question 13 :-Describe an efficient method to merge two balanced binary
search trees with n elements each into a balanced BST. Give its running time.
Answer:-We can start by doing an in-order walk of both trees concurrently. At
each step, we compare the two tree elements and add the smaller one into a
list, L, before calling that element’s successor. When we finish walking both
trees, L will contain a sorted list of elements from both trees. This takes O(n +
n) = O(n) total time. Now, from the sorted list, we want to create a balanced
binary tree, which is the same problem as described in problem set 2. We can
do this by setting the root as the middle element of the list, and letting the first
half of the list be its left subtree and the second half be its right subtree
(recursively creating the balanced subtrees as well). This also takes O(n + n)
= O(n) time. The total time for this algorithm is therefore O(n).
Question 14 :-Ben Bitdiddle recently learned about heaps and binary search
trees in his algorithms class. He was so excited about getting to know about
them, he thought of an interesting way to combine them to create a new
hybrid binary tree called a treap. The treap T has a tuple value stored at each
node (x, y) where he calls x the key, and y the priority of the node. The keys
follow the BST property (maintain the BST invariant) while the priorities
maintain the min-heap property. An example treap is shown below:

Answer:-Insert the new node according to the standard BST INSERT procedure. This
preserves the BST property, but may result in a violation of the heap property. Now,
we need to fix the heap property by moving the new node up in the treap until it
reaches the correct place. Do this by repeatedly rotating on the node’s parent, moving
the node up one level while preserving the BST invariant. The BST insertion requires
O(h) time. Each rotation takes O(1), and O(h) rotations are required, so the total
insertion time is O(h).
Question 15 :-Demonstrate what happens when we insert the keys
5,28,19,15,20,33,12,17,10into a hash table with collisions resolved by chaining. Let the table
have 9 slots, and let the hash function be h(k)=kmod9.

Solution:
Let us number our slots 0,1,…,8.
Then our resulting hash table will look like following:

Question – 16 ts) Say the following tree was obtained by inserting the element
42 into an AVL tree. The tree no longer satisfies the AVL invariant, but the
invariant can be reestablished by performing two rotate operations. Show the
resulting tree after this is done

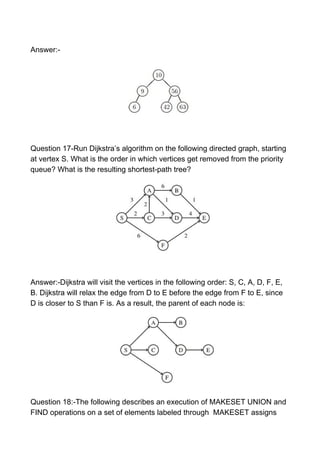
Answer:-
Question 17-Run Dijkstra’s algorithm on the following directed graph, starting
at vertex S. What is the order in which vertices get removed from the priority
queue? What is the resulting shortest-path tree?
Answer:-Dijkstra will visit the vertices in the following order: S, C, A, D, F, E,
B. Dijkstra will relax the edge from D to E before the edge from F to E, since
D is closer to S than F is. As a result, the parent of each node is:
Question 18:-The following describes an execution of MAKESET UNION and
FIND operations on a set of elements labeled through MAKESET assigns

rank to an element and UNION breaks ties by putting the tree whose root has
the larger label as the parent of the other.
for j= 1 to 10
MAKESET(j)
end for
UNION(1,2) ; UNION(1,3); UNION(4,5); UNION(4,6); UNION(1,6); UNION(7,8);
UNION(9,10); UNION(7,10); UNION(3,8); FIND(4); FIND(3);
Give the tree from executing the above steps using union-by-rank with no
path-compression Be sure to label the nodes in the final tree including their final ranks.
Give the tree from executing the above steps using union-by-rank with path-compression
Be sure to label the nodes in the final tree including their final ranks.
Answer:
Question:19 ) Draw the Huffman tree corresponding to the encoding table below.
char freq encoding
B 2 01111
F 1 01110
H 3 0110
I ? 00
L 5 010
M 15 10
S 15 11
which one or more of the following are possible values for the frequency of the character I.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Answer:

6 ≤ freq(I) ≤ 15.
Since I is not touched until after merging L with {B, F, H}, freq(I) ≥ freq(L) = 5 and freq(I) ≥
freq({B, F, H}) = 2 + 1 + 3 = 6. • Since I is merged with {B, F, H, L} instead of M or S, freq(I)
≤ freq(M) = 15 and freq(I) ≤ freq(S) = 15
Question 20:-What is the max-heap resulting from performing on the node storing 6?
Answer: will swap 6 with its larger child until 6 reaches a position where it satisfies the
max-heap property. The correct heap is:

Question 21:-What binary search tree is obtained after the root of this tree is deleted?
Answer:- The correct algorithm replaces 7 with the successor (next-largest) node of 7,
which is 10. The right subtree of 10 is moved to the location 10 was originally in.
Alternatively, you can replace 7 with its predecessor 6. (If 6 had a left subtree, it would be
moved to where 6 was originally.)

A common mistake on this problem was to use something resembling , recursively moving
the larger child up to replace the deleted parent. This does not result in a valid BST.
Question 22:
1) The number of distinct minimum spanning trees for the weighted graph below is

Answer:Highlighted (ingreen) are the edges picked to make a MST. In the right side of
MST, we could either pick edge ‘a’ or ‘b’. In the left side, we could either pick ‘c’ or ‘d’ or ‘e’
in MST.
There are 2 options for one edge to be picked and 3 options for another edge to be picked.
Therefore, total 2*3 possible MSTs.

Question 23:-What is the number of binary search trees with 20 nodes with elements 1, 2,
3,…..20 such that the root of tree is 12 and the root of left subtree is 7?

Answer:Number of nodes in left subtree = 11 {1, 2, 3, 4….11}
Number of nodes in the right subtree = 8 {13, 14, ….20}
Since for the left subtree root is 7
Number of elements in the left part of left subtree = 6 {1, 2, 3..6}
Number of elements in the right part of left subtree = 4 {8, 9, 10, 11}
We know number of Binary Search trees with n nodes = (C(2n,n)/n+1)
Number of BST with 6 nodes = (C(12,6)/7) = 132
Number of BST with 4 nodes = (C(8,4)/5) = 14
Number of BST with 8 nodes = (C(16,8)/9) =1430
Total number of BST = 2642640

Question 24:-Which among the following is max-heap ?Explain the reason why it is and
Why it is not ?

Answer:A binary tree is max-heap if it is a complete binary tree (A complete binary tree is a
binary tree in which every level, except possibly the last, is completely filled, and all nodes
are as far left as possible) and it follows the max-heap property (value of each parent is
greater than or equal to the values of its children).
A) is not a max-heap because it is not a complete binary tree
B) is a max-heap because it is a complete binary tree and follows max-heap property.
C) is not a max-heap because 8 is a child of 5 in this tree, so violates the max-heap
property.
D) is not a max-heap because 8 is a child of 5 in this tree, so violates the max-heap
property. There are many other nodes in this tree which violate max-heap property in this
tree.
Question 25:-Consider a hash table with 9 slots. The hash function is h(k) = k mod 9. The
collisions are resolved by chaining. The following 9 keys are inserted in the order: 5, 28, 19,
15, 20, 33, 12, 17, 10. What is the maximum, minimum, and average chain lengths in the
hash table.

Answer:-Following are values of hash function for all keys
5---->5
28----->1
19------>1{chained with 28}
15------->6
20------>2
33------>6{chained with 15}
12------>3
17--------->8

10--------->1{chained with 28 and 19}
The maximum chain length is 3. The keys 28, 19 and 10 go to the same slot 1, and form a
chain of length 3.
The minimum chain length 0, there are empty slots (0, 4 and 7).
Average chain length is (0 + 3 + 1 + 1 + 0 + 1 + 2 + 0 + 1)/9 = 1

Question 26:-

Use Kruskal’s algorithm to find a minimum spanning tree (MST) for the network shown
above. You should list the edges in the order in which you consider them. In each case,
state whether you are adding the edge to your MST. Draw the resultant MST
Answer:-
Solution
Edges (in order of consideration Add?
AB Yes
DE Yes
BC Yes
AC No
BD Yes
BE No

CE No
CF Yes
FE No
DF No
BF No
Resultant MST:
Note: As there are edges with equal weights, there may be multiple correct answers
possible
Question 27:-
a) Insert 84 in the given below AVL tree. Re-draw the tree.
b) Delete 66 from the resultant tree in (a). Re-draw the tree.
Solution:-
or (for deletion using predecessor)

Question 28 Perform topological sort for below DAG. Provide at least two orderings by showing
the discovery and finishing times of visit for each node.
Solution
Ordering 1: G A B D C E F
A B C D E F G
D(t) 1 2 3 9 4 5 13
F(t) 12 11 8 10 7 6 14
Ordering 2: A B C G D E F
A B C D E F G
D(t) 9 10 11 2 3 4 1
F(t) 14 13 12 7 6 5 8
(Optional) Other possible ordering: GABCDEF)
Question 29:-

a) Even though the graph has negative weight edges, step through Dijkstra’s algorithm to
calculate supposedly shortest paths from A to every other vertex. Show your steps. Cross
out old values and write in new ones, from left to right within each cell, as the algorithm
proceeds. Also list the vertices in the order in which you marked them as known.
Solution:
Correct Order ( 2 Marks, binary ) = A, B, D, F, C, G, E
Distances { 3 mark for all correct,
2 marks if done extra reps,
0 marks otherwise
[ some exceptions on checker discretion ]
}
A 0
B 2
C 7
D 4
E 12 , 9
F 6
G 8 , 2
b) Dijkstra’s algorithm found the wrong path to some of the vertices. For just the vertices
where the wrong path was computed, indicate both the path that was computed and the
correct path. [3 marks]
A->D
A->F
Any one correct 1.5 marks

Both Correct 3 marks
Mentioned any wrong one with D and F 2.5 marks
c) What single edge could be removed from the graph such that Dijkstra’s algorithm would
happen to compute correct answers for all vertices in the remaining graph.
Solution:
c) The edge E to G
Question 30:-Delhi Traffic Police has made all roads one way. The CM claims that there is still a
legal way to drive from one point of the city to another. The opposition is not convinced and argues
the CM’s claim to be false. Formulate this problem as a graph problem and give a linear time
algorithm to check the validity of the claim. Explain the time complexity of your algorithm.
Answer:-This problem could be represented as a directed graph with the vertices as the points in
the city and edge from point A to B representing the oneway road in direction from A to B. The task
is to check if for all pairs of vertices there exists a path or not. This is clearly a problem on SCC. If
the entire road network(the graph) is one SCC then the CM’s claim is true, else false.
Algorithm1.
Compute finishing time for every vertex by calling DFS on graph. Store these vertices in
decreasing order of their finishing time in a List L.
2. Reverse the direction of every edge to get a graph G’
3. Run DFS on G’, selecting vertices as stored in order in List L. Maintain a counter(initialized to 0)
and for a depth first tree obtained from every white vertex, increment the counter by 1.
4. If after step 3, counter =1 => CM’s claim is true, else false
Time Complexity: O(V+E) as DFS has time complexity of O(V+E) step 1 and step 3 take O(V+E) ,
step 2 is O(E), step 4 is O(1). Note that this is linear time in terms of size of graph(including the
edges and vertices)
Question 31:-Assume this tree is a binary search tree even though you cannot see what the keys
and values are at the nodes (the letters we write below are just “names” for the nodes for the
purpose of answering the questions).

(a) What node is the successor of node A?
(b) What node is the successor of node B?
(c) What node is the successor of node C?
(d) What is the height of the tree?
(e) What is the maximum number of nodes that could be added to the tree without increasing its
height?
(f) Is the tree an AVL tree?
(g) If we remove only node H, is the result an AVL tree?
(h) If we remove only node J, is the result an AVL tree?
(i) If we remove only node K, is the result an AVL tree?
Answer:-(a) J
(b) E
(c) K
(d) 4
(e) 18
(f) yes
(g) yes
(h) no
(i) no
Question 32:- Suppose there is a binary min-heap with exactly 4 nodes, containing items with
priorities 3, 9, 11, and 15.
(a) Show every possible binary min-heap that could match this description. For each, draw the
appropriate tree and the array representation. (You can show just the priorities, not the
corresponding items.)
(b) For one of your answers to part (a), show what happens with 4 deleteMin operations. Clearly
indicate which heap you are starting with and show the heap after each deleteMin. You can just
draw the tree (not the array) after each step.
Solution:

Explanation: All 4-node heaps must have the shape of the 3 heaps in part (a). The minimum node,
3, must be at the root. The maximum node, 15, must be at a leaf. The only heap meeting these
rules and not listed above does not satisfy the heap property because 11 is above 9:
Question 33:-

DSA (Data Structure and Algorithm) Questions

Recommended

More Related Content

What's hot (20)

Similar to DSA (Data Structure and Algorithm) Questions (20)

More from RESHAN FARAZ (12)

Recently uploaded (20)

DSA (Data Structure and Algorithm) Questions