Efficient algorithm for rsa text encryption using cuda c

Dhinaharan Nagamalai et al. (Eds) : ACITY, WiMoN, CSIA, AIAA, DPPR, NECO, InWeS - 2014
pp. 233–241, 2014. © CS & IT-CSCP 2014 DOI : 10.5121/csit.2014.4524
EFFICIENT ALGORITHM FOR RSA TEXT
ENCRYPTION USING CUDA-C
Sonam Mahajan1
and Maninder Singh2
1,2
Department of Computer Science Engineering, Thapar University, Patiala,
India
sonam_mahajan1990@yahoo.in
msingh@thapar.edu
ABSTRACT
Modern-day computer security relies heavily on cryptography as a means to protect the data
that we have become increasingly reliant on. The main research in computer security domain
is how to enhance the speed of RSA algorithm. The computing capability of Graphic Processing
Unit as a co-processor of the CPU can leverage massive-parallelism. This paper presents a
novel algorithm for calculating modulo value that can process large power of numbers
which otherwise are not supported by built-in data types. First the traditional algorithm is
studied. Secondly, the parallelized RSA algorithm is designed using CUDA framework. Thirdly,
the designed algorithm is realized for small prime numbers and large prime number . As a
result the main fundamental problem of RSA algorithm such as speed and use of poor or
small prime numbers that has led to significant security holes, despite the RSA algorithm's
mathematical soundness can be alleviated by this algorithm.
KEYWORDS
CPU, GPU, CUDA, RSA, Cryptographic Algorithm.
1. INTRODUCTION
RSA (named for its inventors, Ron Rivest, Adi Shamir, and Leonard Adleman [1] ) is a public
key encryption scheme. This algorithm relies on the difficulty of factoring large numbers which
has seriously affected its performance and so restricts its use in wider applications. Therefore, the
rapid realization and parallelism of RSA encryption algorithm has been a prevalent research
focus. With the advent of CUDA technology, it is now possible to perform general-purpose
computation on GPU [2]. The primary goal of our work is to speed up the most computationally
intensive part of their process by implementing the GCD comparisons of RSA keys using
NVIDIA's CUDA platform.
The reminder of this paper is organized as follows. In section 2, we study the traditional RSA
algorithm. In section 3, we explained our system hardware. In section 4, we explained the design
and implementation of parallelized algorithm. Section 5 gives the result of our parallelized
algorithm and section 6 concludes the paper.

234 Computer Science & Information Technology (CS & IT)
2. TRADITIONAL RSA ALGORITHM[1]
RSA is an algorithm for public-key cryptography [1] and is considered as one of the great
advances in the field of public key cryptography. It is suitable for both signing and encryption.
Electronic commerce protocols mostly rely on RSA for security. Sufficiently long keys and up-to-
date implementation of RSA is considered more secure to use.
RSA is an asymmetric key encryption scheme which makes use of two different keys for
encryption and decryption. The public key that is known to everyone is used for encryption. The
messages encrypted using the public key can only be decrypted by using private key. The key
generation process of RSA algorithm is as follows:
The public key is comprised of a modulus n of specified length (the product of primes p and q),
and an exponent e. The length of n is given in terms of bits, thus the term “8-bit RSA key" refers
to the number of bits which make up this value. The associated private key uses the same n, and
another value d such that d*e = 1 mod φ (n) where φ (n) = (p - 1)*(q - 1) [3]. For a plaintext M
and cipher text C, the encryption and decryption is done as follows:
C= Me
mod n, M = Cd
mod n.
For example, the public key (e, n) is (131,17947), the private key (d, n) is (137,17947), and let
suppose the plaintext M to be sent is: parallel encryption.
• Firstly, the sender will partition the plaintext into packets as: pa ra ll el en cr yp ti on. We
suppose a is 00, b is 01, c is 02, ..... z is 25.
• Then further digitalize the plaintext packets as: 1500 1700 1111 0411 0413 0217 2415
1908 1413.
• After that using the encryption and decryption transformation given above calculate the
cipher text and the plaintext in digitalized form.
• Convert the plaintext into alphabets, which is the original: parallel encryption.
3. ARCHITECTURE OVERVIEW[4]
NVIDIA's Compute Unified Device Architecture (CUDA) platform provides a set of tools to
write programs that make use of NVIDIA's GPUs [3]. These massively-parallel hardware devices
process large amounts of data simultaneously and allow significant speedups in programs with
sections of parallelizable code making use of the Simultaneous Program, Multiple Data (SPMD)
model.

Computer Science & Information Technology (CS & IT) 235
Figure 1. CUDA System Model
The platform allows various arrangements of threads to perform work, according to the
developer's problem decomposition. In general, individual threads are grouped into up-to 3-
dimensional blocks to allow sharing of common memory between threads. These blocks can then
further be organized into a 2-dimensional grid. The GPU breaks the total number of threads into
groups called warps, which, on current GPU hardware, consist of 32 threads that will be executed
simultaneously on a single streaming multiprocessor (SM). The GPU consists of several SMs
which are each capable of executing a warp. Blocks are scheduled to SMs until all allocated
threads have been executed. There is also a memory hierarchy on the GPU. Three of the various
types of memory are relevant to this work: global memory is the slowest and largest; shared
memory is much faster, but also significantly smaller; and a limited number of registers that each
SM has access to. Each thread in a block can access the same section of shared memory.
4. PARALLELIZATION
The algorithm used to parallelize the RSA modulo function works as follows:
• CPU accepts the values of the message and the key parameters.
• CPU allocates memory on the CUDA enabled device and copies the values on the device
• CPU invokes the CUDA kernel on the GPU
• GPU encrypts each message character with RSA algorithm with the number of threads
equal to the message length.
• The control is transferred back to CPU
• CPU copies and displays the results from the GPU.
As per the flow given above the kernel is so built to calculate the cipher text C = Me
mod n. The
kernel so designed works efficiently and uses the novel algorithm for calculating modulo value.
The algorithm for calculating modulo value is implemented such that it can hold for very large

power of numbers which are not supported by built in data types. The modulus value is calculated
using the following principle:
• C = Me
mod n
• C = (Me-x
mod n * Mx
mod n) mod n
Hence iterating over a suitable value of x gives the desired result.
4.1. Kernel code
As introduced in section 2, RSA algorithm divides the plaintext or cipher text into packets of
same length and then apply encryption or decryption transformation on each packet. A question is
how does a thread know which elements are assigned to it and are supposed to process them?
CUDA user can get the thread and block index of the thread call it in the function running on
device. In this level, the CUDA Multi-threaded programming model will dramatically enhanced
the speed of RSA algorithm. The experimental results will be showed in section 5.
The kernel code used in our experiment is shown below. First CUDA user assign the thread and
block index, so as to let each thread know which elements they are supposed to process. It is
shown in Figure 2. Then it call for another device function to calculate the most intense part of
the RSA algorithm. Note in the below figure2 and figure3, it works for 3 elements.
Figure 2. Kernel code

Figure 3. Kernel’s Device code
5. VERIFICATION
In this section we setup the test environment and design three tests. At first test, we develop a
program running in traditional mode for small prime numbers (only use CPU for computing).
And at the second test, we use CUDA framework to run the RSA algorithm for small prime
numbers in multiple-thread mode. Comparison is done between the two test cases and speed up is
calculated. In the third test we run the GPU RSA for large prime numbers that is not supported
by the built-in data types of CPU RSA. The test result will be showed in this section
5.1. Test environment
The code has been tested for :
• Values of message between 0 and 800 which can accommodate the complete ASCII
table
• 8 bit Key Values
The computer we used for testing has an Intel(R) Core(TM) i3-2370M 2.4GHZ CPU, 4 GB
RAM, Windows 7OS and a Nvidia GeForce GT 630M with 512MB memory, and a 2GHZ DDR2
memory. At the first stage, we use Visual Studio 2010 for developing and testing the traditional
RSA algorithm using C language for small prime numbers. Series of input data used for testing
and the result will be showed later.

At the second stage, we also use Visual Studio 2010 for developing and testing parallelized RSA
developed using CUDA v5.5 for small prime numbers. After that the results of stage one and
stage second are compared and hence calculating the respective speedup.
In the third test we run the GPU RSA for large prime numbers that is not supported by the built-in
data types of CPU RSA. The test result will be showed in this section. At present the calculation
of Cipher text using an 8-bit key has been implemented parallel on an array of integers.
5.2 Results
In this part, we show the experiment results for GPU RSA and CPU RSA for small value of n.
Table 1. Comparison of CPU RSA and GPU RSA for small prime numbers i.e (n=131*137)
Table 1 shows the relationship between the amount of data inputting to the RSA algorithm and
the execution times (in seconds) in traditional mode and multiple thread mode. The first column
shows the number of the data input to the algorithm, and the second column shows the number of
blocks used to process the data input. In the above table 64 threads per block are used to execute
RSA. The execution time is calculated in seconds. In the last column speed up is calculated.
Above results are calculated by making average of the results so taken 20 times to have final
more accurate and precise results.
The enhancement of the execution performance using CUDA framework can be visually
demonstrated by Fig 4.
Figure 4. Graph showing effect of data input on CPU RSA and GPU RSA along with the Speedup

5.2.1 GPU RSA for large prime numbers
In this part, we show the experiment results for GPU RSA and CPU RSA for small value of n.
Table 2. GPU RSA for large prime numbers and large value of n (n = 1005 * 509)
From Table 2, we can see the relationship between the execution time in seconds and the input
data amount (data in bytes) is linear for certain amount of input. When we use 256 data size to
execute the RSA algorithm, the execution time is very short as compared to traditional mode
which is clearly proved in the above section where the comparison is made for CPU RSA and
GPU RSA for small prime numbers and hence for small value of n. So we can say when the data
size increases, the running time will be significantly reduced depending upon the number of
threads used. Furthermore, we also find that when the data size increases from 1024 to 8192, the
execution time of 7168 threads almost no increase, which just proves our point of view, the more
the data size is, the higher the parallelism of the algorithm, and the shorter the time spent.
Execution time varies according the number of threads and number of blocks used for data input.
In the above table threads per block are constant i.e we use 32 threads per block and number of
blocks used are adjusted according to the data input.
The enhancement of the execution performance of data input in bytes using the large value of
prime numbers (n=1009 * 509) and hence large value of n on CUDA framework can be visually
demonstrated by Figure 5.
Figure 5. GPU RSA for large value of n (n=1009*509)
5.2.2. Execution time comparison of GPU RSA for large value of n (1009*509) with CPU
RSA for small value of n(137*131)
In the third and final stage of test results analysis, we analyse our results between sequential RSA
that is using small value of n (17947) and parallelized RSA that is making use of large prime

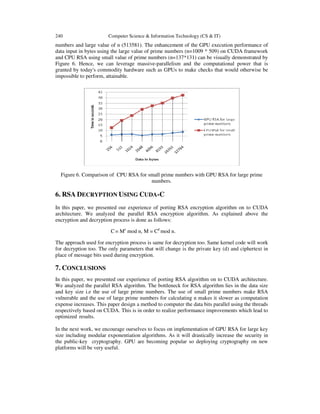
numbers and large value of n (513581). The enhancement of the GPU execution performance of
data input in bytes using the large value of prime numbers (n=1009 * 509) on CUDA framework
and CPU RSA using small value of prime numbers (n=137*131) can be visually demonstrated by
Figure 6. Hence, we can leverage massive-parallelism and the computational power that is
granted by today's commodity hardware such as GPUs to make checks that would otherwise be
impossible to perform, attainable.
Figure 6. Comparison of CPU RSA for small prime numbers with GPU RSA for large prime
numbers.
6. RSA DECRYPTION USING CUDA-C
In this paper, we presented our experience of porting RSA encryption algorithm on to CUDA
architecture. We analyzed the parallel RSA encryption algorithm. As explained above the
encryption and decryption process is done as follows:
C= Me
mod n, M = Cd
mod n.
The approach used for encryption process is same for decryption too. Same kernel code will work
for decryption too. The only parameters that will change is the private key (d) and ciphertext in
place of message bits used during encryption.
7. CONCLUSIONS
In this paper, we presented our experience of porting RSA algorithm on to CUDA architecture.
We analyzed the parallel RSA algorithm. The bottleneck for RSA algorithm lies in the data size
and key size i.e the use of large prime numbers. The use of small prime numbers make RSA
vulnerable and the use of large prime numbers for calculating n makes it slower as computation
expense increases. This paper design a method to computer the data bits parallel using the threads
respectively based on CUDA. This is in order to realize performance improvements which lead to
optimized results.
In the next work, we encourage ourselves to focus on implementation of GPU RSA for large key
size including modular exponentiation algorithms. As it will drastically increase the security in
the public-key cryptography. GPU are becoming popular so deploying cryptography on new
platforms will be very useful.

REFERENCES
[1] R. L. Rivest, A. Shamir, and L. Adleman. A method for obtaining digital signatures and public-key
cryptosystems. Communications of the ACM, 21(2):120{126, 1978.
[2] J. Owens, D. Luebke, N. Govindaraju.. A survey of general-purpose computation on graphics
hardware. Computer Graphics Forum, 26(1): 80{113 , March 2007.
[3] N. Heninger, Z. Durumeric, E. Wustrow, and J. A. Halderman. Mining your Ps and Qs: detection of
widespread weak keys in network devices. In Proceedings of the 21st USENIX conference on
Security symposium, pages 205{220. USENIX Association, 2012 .
[4] NVIDIA|CUDA documents |Programming Guide |CUDA v5.5.
http://docs.nvidia.com/cuda/pdf/CUDA_C_Programming_Guide.pdf
AUTHORS
Sonam Mahajan
Student , ME – Information Security
Computer Science and Engineering Department
Thapar University
Patiala-147004
Dr. Maninder Singh
Associate Professor
Computer Science and Engineering Department
Thapar University
Patiala-147004

Efficient algorithm for rsa text encryption using cuda c

Recommended

More Related Content

What's hot (20)

Viewers also liked (18)

Similar to Efficient algorithm for rsa text encryption using cuda c (20)

Recently uploaded (20)

Efficient algorithm for rsa text encryption using cuda c