Engineering.CSE.DataStructure.Linkedlist.notes

Course code: BTCOC303
Course Coordinator: Mrs. D. D. Dhokate
Data Structures

Introduction
 List refers to a linear collection of data items.
 Frequently items get added or deleted from the list.
 Data processing involves storing and processing data
organized into lists.
 There are two ways to represent link.

A)
 Array is one way for storing data
 Linear relationship between data elements is reflected by
physical relationship of data in memory, not by information
contains in data elements.
 Elements are stored at consecutive memory locations.
 Inserting and deleting the data elements in an array is
relatively expensive.
 Array occupies the block of memory space
 Size of the array can not be changed as per requirement .
Introduction

Introduction
B)
 Another way of storing a list in the memory is to have
each element in the list contain a field called ‘link’ or
pointer, which contains the address of the next element in
the list.
 Successive elements in the list need not occupy adjacent
space in the memory.
 Inserting and deleting in the list is easier.

Linked List
 The special list of data elements which are linked to one
another.
 Logical ordering is represented by having each element
pointing to the next elements.
 Linked list is a linear collection of data elements called
‘nodes’ where the linear order is given by means of
pointers.
67 NEXT/POINTER/LINK
89 NEXT/POINTER/LINK

Types of Linked List:
 Singly Linked List
 Doubly Linked List
Linked List

Types of Linked List:
 Circular Linked List
 Circular Doubly Linked List
Linked List

Each node is divided is divided in two parts.
Info/Data field – Stores the information of the element.
Link field / Next pointer field /Pointer – Contains address of next
node in the list.
Singly Linked List

34 6000
67 7074
56 9090
45 X 500 10100
START
5020
5020
6000
7074
9090
10100

 The pointer of the last node contains a special value called
“Null Pointer’ which is any invalid address.
 The Null pointer is denoted by X, signals the end of list.
 Liked list also contains a list pointer variable called
‘START ’or ‘NAME’ which contains the address of the
first node in the list.
 Only this address in the START is needed to trace through
the list.
 If list has no nodes, then list is called ‘Null List’ or
‘Empty’ & is denoted by the null pointer in the variable
START.

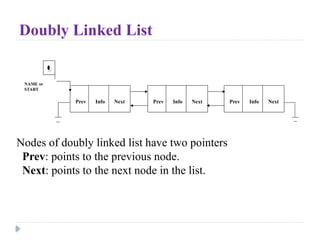
Prev Info Next Prev Info Next Prev Info Next
NAME or
START
Nodes of doubly linked list have two pointers
Prev: points to the previous node.
Next: points to the next node in the list.
Doubly Linked List

Advantages:
 Linked lists are dynamic data structure:
They can grow or shrink during execution of the program
 Efficient memory utilization:
 Memory is not preallocated. Memory is allocated whenever it is
required.
 It is deallocated when it is no longer needed.
 Insertion and deletion are easier and efficient:
Linked list provides flexibility in inserting data item at a
specified position and deletion of a data item from given position.
 Many complex applications can be easily came out with
linked list.

Disadvantages:
 More Memory: If the number of fields are more,
memory space is needed.

Representation of Linked List in memory
 Let LIST be a linked list.
 LIST will be maintained in memory, unless and otherwise
specified or implies as follows.
 LIST requires two Linear Arrays:
 INFO
 LINK
 i.e. INFO[K] & LINK[K] contains respectively
information part and next pointer field of a node of LIST.
 LIST also requires variable START which contains the
location of the beginning of the
 list.

 To store list of integer numbers, then linear list can be
represented in memory with following declarations.
struct node
{
int a;
struct node *next;
};
struct node NODE;
NODE * start;
Representation of Linked List in
memory

Operations on Linked List
 Creation:
 Used to create a Linked List.
 Constituent node is created as and when is required and linked to the list
to preserve the integrity of the list.
 Insertion:
 Used to insert a new node in the Linked List at the specified positions.
 At the beginning of the Linked List
 At the end of the Linked List
 At the specified position in the Linked List
 If the list is empty, then new node is inserted as first node
 Deletion:
 Used to delete node from Linked List.
 From beginning of the Linked List
 From end of the Linked List
 From the specified position in the Linked List

Operations on Linked List
 Traversing:
 Process of going through all nodes of a Linked List from one
end to other end.
 Start from very first node towards last node, it is called
‘Forward Traversing’.
 Concatenation:
 Process of appending the second list to the end of first list
containing m nodes.
 If the second list has n nodes, then concatenated list contains
(m+n) nodes.
 Display:
 Used to print each and every nodes information.

Traversing a Linked List
 Let LIST be a Linked List in memory stored in Linear
Arrays INFO and LINK with START pointing to the first
element and NULL indicating the end of List.
 Traversing algorithm uses a pointer variable PTR which
points to the node that is currently being processed.
 i.e LINK[PTR] points to the next node to be processed
PTR := LINK[PTR]
 It moves pointer to the next node in the List.

34 6000
67 7074
56 9090
45 X 500 10100
START
5020
5020
6000
7074
9090
10100
PTR
X

Engineering.CSE.DataStructure.Linkedlist.notes

Details of Algorithm:
 Initialize PTR or START
 Process INFO [PTR], the information at first node.
 Update PTR by the assignment PTR : = LINK [PTR], so
that PTR points to the next node.
 INFO [PTR] gives information at second node.
 Continue updating of PTR until PTR=NULL which
signals end of List.

1. Set PTR:= START [ Initialize pointer PTR]
2. Repeat steps 3 & 4 while PTR ≠ NULL
3. Apply PROCESS to INFO[PTR]
4. Set PTR:=LINK[PTR]
5. [ PTR now points to next node]
6. [ End of Step 2 Loop]
7. Exit
Algorithm for Traversing a Linked List
Let LIST be a Linked List in memory. This algorithm traverses LIST, applying a
operation PROCESS to each element of LIST. The variable PTR points to the nod
currently being processed.

Info Link Info Link Info X
START
PTR 3. Apply PROCESS to INFO[PTR]

START
PTR
4. Set PTR:=LINK[PTR]
[ PTR now points to next node]

START
PTR
Repeat steps 3 & 4 while PTR ≠ NULL

Procedure to print the information at each node
Procedure: PRINT (INFO,LINK, START)
This procedure prints information at each node
1 Set PTR:= START [ Initialize pointer PTR]
2 Repeat steps 3 & 4 while PTR ≠ NULL
3 Write : INFO[PTR]
4 Set PTR:=LINK[PTR]
[ Updates PTR]
[ End of Step 2 Loop]
5 Return

Procedure to find the number of elements in a Linked List
Procedure: COUNT (INFO,LINK, START,NUM)
This procedure prints information at each node
1 Set NUM := 0 [ Initialize Counter]
2 Set PTR:= START [ Initialize pointer PTR]
3 Repeat steps 4& 5while PTR ≠ NULL
4 Set NUM:=NUM+1
[ Increase NUM by 1]
5 Set PTR:=LINK[PTR] [ Updates PTR]
[ End of Step3 Loop]
6 Return

Searching in a Linked List
 There are two searching algorithms for finding LOC
of node where ITEM first appears in LIST.
 First algorithm does not assume that data in LIST are sorted
 Second algorithm assumes that LIST is sorted.

Algorithm for searching an ITEM
SEARCH (INFO, LINK, START, ITEM, LOC)
LIST is a Linked List in memory.This algorithm finds the location LOC
of the node where ITEM first appears in LIST or sets LOC=NULL.
2. Repeat steps 3 while PTR ≠ NULL
3. If ITEM = INFO[PTR] then:
Set LOC: =PTR and Exit
Else:
Set PTR: =LINK [PTR] [PTR points to next node]
[End of Step 2 Loop]
4 . [Search is unsuccessful] Set LOC:=NULL
5. Exit

Algorithm for searching an ITEM when List is sorted
SEARCH (INFO, LINK, START, ITEM, LOC)
LIST is a Linked List in memory. This algorithm finds the location LOC of the
node where, ITEM first appears in LIST or sets LOC=NULL.
2. Repeat steps 3 while PTR ≠ NULL
3. If ITEM > INFO[PTR] then:
Set PTR: =LINK [PTR] [PTR points to next node]
Else if ITEM = INFO[PTR] then:
Set LOC: =PTR and Exit
Else:
Set PTR: =NULL and Exit [ ITEM does not exists]
[End of If structure]
[End of Step 2 Loop]
4. Set LOC:=NULL
5. Exit

Memory Allocation: Garbage Collection
 The maintenance of Linked Lists in memory require some
mechanism which provides unused memory space for the
new nodes or mechanism is required whereby the memory
space of deleted nodes becomes available for future use.
 Together with the linked lists in memory, a special list is
maintained which consists of unused memory cells.
 The list has its own pointer.
 List is called as ‘List of available space’ or ‘free storage
list’ or ‘ free pool’.

 Assume Linked lists are implemented by parallel arrays
and insertion and deletion are performed on the linked
lists.
 The unused memory cells in the array will also be linked
together to form a linked list using AVAIL as its list
pointer variable.

LIST(INFO, LINK, START, AVAIL)

Garbage Collection
 Some memory space becomes reusable because a node is
deleted from a list or an entire list is deleted from a program.
 The space can be available for future use.
 This can be achieved by immediately reinserting the space into
the free storage list.
 This can be done only when linked list is implemented by
means of linear arrays.
 This method is too much time consuming for operating system
of a computer.
 The alternative way is as: The operating system of a computer
may be periodically collect all deleted space onto the free
storage list. This technique is called ‘Garbage Collection’.

Garbage Collection
 Garbage Collection is carried out in two steps:
 Computer runs through all lists, tagging those cells which are
currently in use.
 Then, computer runs through the memory, collecting all
untagged space onto free storage list.
 The garbage collection may take place when there is only some
minimum amount of space or no space at all left in the free
storage list or when the CPU is idle and has time to do the
collection.
 Garbage collection is invisible to programmer.

Overflow and Underflow
 Overflow:
 Sometimes new data are to be inserted into data structure but there
is no available space. i.e. free storage list is empty. Programmer
may handle overflow by printing the message OVERFLOW.
 Overflow will occur with our linked list when AVAIL = NULL and
there is an insertion.
 Underflow:
 Situation where one wants to delete data from a data structure that
is empty.
 Underflow can be handled by printing the message UNDERFLOW.
 Underflow will occur with our linked list when START = NULL
and there is deletion.

The Scenario
 You have a linked list
 Perhaps empty, perhaps not
 Perhaps ordered, perhaps not
 You want to add an element into
the linked list
48 17 142
head
//

Adding an Element to a Linked List
Involves two steps:
 Finding the correct location
 Doing the work to add the node

Finding the Correct Location
 Three possible positions:
 The front
 The end
 Somewhere in the middle

head
Inserting to the Front
 There is no work to find the correct
location
 Empty or not, head will point to the
right location
48 17 142
START 93

Inserting to the End
 Find the end of the list
(when at NIL)
 Recursion or iteration
48 17 142
START
//93
//
Don’t Worry!

Inserting to the Middle
 Used when order is important
 Go to the node that should follow the
one to add
 Recursion or iteration
17 48 142
START
//
93
//
142

Insertion into Linked Lists
START X
Node A Node B
New node N is to be inserted into list between nodes A and B
Linked list with successive nodes A & B
START X
Node A Node B
Node N
Node A points to the new node N New node N points to node B,
to which A previously pointed

 Linked list is maintained on memory in the form
LIST (INFO, LINK, START, AVAIL)
 The first node in the AVAIL list will be used for new node N.
 The nextponiter field of node A now points to the new node N,
to which AVAIL previously pointed.
 AVAIL now points to second node in free pool, to which node
N previously pointed.
 The nextponiter field of node N now points to node B, to which
node A previously pointed
.

START X
Node A Node B
New node N is to be inserted into list between nodes A and B
Linked list with successive nodes A & B
AVAIL X
Node N
Node A points to the new node N
New node N points to node B,
to which A previously pointed
Free Storage List

Insertion Algorithm
 Insertion algorithm will use node in the AVAIL list.
Therefore all the algorithms will include following steps
 Checking the availability of space in the AVAIL list. If the
space is not available i.e. AVAIL = NULL, then the algorithm
will print the message OVERFLOW.
 Removing the first node from the AVAIL list. Using the
variable NEW to keep track the location of the new node, this
step can be implemented by pair of assignments.
 NEW:=AVAIL, AVAIL:=LINK[AVAIL]
 Linked may be empty or not. Also Linked list may be
ordered or not.

Algorithm for Inserting to the Front
INSERT (INFO, LINK, START, AVAIL, ITEM)
This algorithm inserts ITEM as the first node in the list
1. [OVERFLOW?] If AVIAL =NULL, then: Write:
OVERFLOW, and Exit
2. [Remove first node from AVAIL list]
Set NEW:=AVAIL and AVAIL :=LINK[AVAIL]
3. Set INFO [NEW]: = ITEM [Copies new data into
new node]
4. Set LINK [NEW]: = START [New node points to
original first node]
5. Set START: = NEW [ Changes START so it points to
the new node]
6 .Exit

START X
(New node N is to be inserted at front)
AVAIL X
AVAIL:=LINK[AVAIL]
Free Storage List
NEW
NEW:=AVAIL
67
INFO[NEW]=ITEM
START
LINK [NEW]=START
START=NEW

START X
Linked list with new nod added at front
AVAIL X
Free Storage List
67

Algorithm for Inserting after a Given Node
INSLOC (INFO, LINK, START, AVAIL, LOC, ITEM)
This algorithm inserts ITEM so that ITEM follows the node with location
LOC or inserts ITEM as the first node when LOC=NULL.
1. [OVERFLOW?] If AVIAL =NULL, then : Write: OVERFLOW, and
Exit
2. [Remove first node from AVAIL list]
Set NEW:=AVAIL and AVAIL :=LINK[AVAIL]
3. Set INFO [NEW]:= ITEM [ Copies new data into new node]
4. If LOC =NULL, then: [Insert as first node]
Set LINK [NEW]:= START and START:=NEW
Else: [Insert after node with location LOC]
Set LINK [NEW]:=LINK[LOC] and LINK [LOC] := New
[End of If Structure]
5. Exit

The Scenario
 Begin with an existing linked list
 Could be empty or not
 Could be ordered or not
4 17
START
42
6

The Scenario
4 17
START
42

The Scenario
4 17
head
42

Deletion from a Linked List
 LIST is a linked list with a node N between nodes A & B as
shown in Figure.
• Schematic Diagram of deletion of Node N is as shown
in Figure

 Linked list is maintained on memory in the form
LIST (INFO, LINK, START,AVAIL)
 When a node is deleted from LIST it will immediately return
its memory space to the AVAIL list. For easier processing, it
will be returned to the beginning of the AVAIL list as shown in
Figure.

 Three pointer fields are changed as follows:
 The nextpointer field of node A now points to node B, where node
N previously pointed.
 The nextpointer field of N now points to the original first node in
the free pool where AVAIL previously pointed.
 AVAIL now points to the deleted node N.
 There are two special cases:
 If the deleted node is the first node in the list, then START will
point to node B.
 If the deleted node N is the last node in the list, the node A will
contain the NULL pointer.

Deletion Algorithm
 All the deletion algorithms assume that the linked list is in
memory in the form LIST (INFO, LINK, START, AVAIL).
 All the deletion algorithms will return the memory space of the
deleted node N to the beginning of the AVAIL list.
 All algorithms will include the following pair of assignments,
where LOC is the location of the deleted node N:
LINK [LOC] := AVAIL and AVAIL := LOC
 These two operations are pictured as shown in Figure

Deleting the Node Following a Given Node
 Assume LIST be a linked list in memory. Suppose location LOC of a node
N in LIST is given or the location LOCP of the node preceding N is given
or when N is the first node, the LOCP=NULL is given.
DEL (INFO, LINK, START, AVAIL, LOC, LOCP)
This algorithm deletes the node N with location LOC. LOCP is the location
of the node
which precedes N or when N is the first node, LOCP=NULL.
1. If LOCP=NULL, then:
Set START: =LINK [START] [ Deletes first node]
Else:
Set LINK [LOCP]:=LINK[LOC] [Deletes node N]
[End of If Structure]
2. [Return deleted node to the AVAIL list.]
Set LINK[LOC]:=AVAIL and AVAIL:=LOC
3. Exit

Engineering.CSE.DataStructure.Linkedlist.notes

Recommended

More Related Content

Similar to Engineering.CSE.DataStructure.Linkedlist.notes (20)

Recently uploaded (20)

Engineering.CSE.DataStructure.Linkedlist.notes