Graph Algorithms - Map-Reduce Graph Processing

Roadmap
• Graph problems and representations
• Parallel breadth-first search
• PageRank

What’s a graph?
• G = (V,E), where
– V represents the set of vertices (nodes)
– E represents the set of edges (links)
– Both vertices and edges may contain additional information
• Different types of graphs:
– Directed vs. undirected edges
– Presence or absence of cycles
• Graphs are everywhere:
– Hyperlink structure of the Web
– Physical structure of computers on the Internet
– Interstate highway system
– Social networks

Source: Wikipedia (Königsberg)

Some Graph Problems
• Finding shortest paths
– Routing Internet traffic and UPS trucks
• Finding minimum spanning trees
– Telco laying down fiber
• Finding Max Flow
– Airline scheduling
• Identify “special” nodes and communities
– Breaking up terrorist cells, spread of avian flu
• Bipartite matching
– Monster.com, Match.com
• And of course... PageRank

6
Ubiquitous Network (Graph) Data
http://belanger.wordpress.com/2007/06/28/
the-ebb-and-flow-of-social-networking/
• Social Network
• Biological Network
• Road Network/Map
• WWW
• Sematic Web/Ontologies
• XML/RDF
• ….
Semantic Search, Guha et. al., WWW’03

Graph Algorithms - Map-Reduce Graph Processing

Graph (and Relational) Analytics
• General Graph
– Count the number of nodes whose degree is equal to 5
– Find the diameter of the graphs
• Web Graph
– Rank each webpage in the webgraph or each user in the twitter graph
using PageRank, or other centrality measure
• Transportation Network
– Return the shortest or cheapest flight/road from one city to another
• Social Network
– Determine whether there is a path less than 4 steps which connects
two users in a social network
• Financial Network
– Find the path connecting two suspicious transactions;
• Temporal Network
– Compute the number of computers who were affected by a particular
computer virus in three days, thirty days since its discovery

Challenge in Dealing with Graph Data
• Flat Files
– No Query Support
• RDBMS
– Can Store the Graph
– Limited Support for Graph Query
• Connect-By (Oracle)
• Common Table Expressions (CTEs) (Microsoft)
• Temporal Table

Native Graph Databases
• Emerging Field
– http://en.wikipedia.org/wiki/Graph_database
• Storage and Basic Operators
– Neo4j (an open source graph database)
– InfiniteGraph
– VertexDB
• Distributed Graph Processing (mostly in-
memory-only)
– Google’s Pregel (vertex centered computation)

Graph analytics industry
practice status
• Graph data in many industries
• Graph analytics are powerful and can bring
great business values/insights
• Graph analytics not utilized enough in
enterprises due to lack of available
platforms/tools (except leading tech
companies which have high caliber in house
engineering teams and resources)

Graphs and MapReduce
• Graph algorithms typically involve:
– Performing computations at each node: based on
node features, edge features, and local link
structure
– Propagating computations: “traversing” the graph
• Key questions:
– How do you represent graph data in MapReduce?
– How do you traverse a graph in MapReduce?

Representing Graphs
• G = (V, E)
• Two common representations
– Adjacency matrix
– Adjacency list

Adjacency Matrices
Represent a graph as an n x n square matrix M
 n = |V|
 Mij = 1 means a link from node i to j
1 2 3 4
1 0 1 0 1
2 1 0 1 1
3 1 0 0 0
4 1 0 1 0
1
2
3
4

Adjacency Matrices: Critique
• Advantages:
– Amenable to mathematical manipulation
– Iteration over rows and columns corresponds to
computations on outlinks and inlinks
• Disadvantages:
– Lots of zeros for sparse matrices
– Lots of wasted space

Adjacency Lists
Take adjacency matrices… and throw away all the zeros
1: 2, 4
2: 1, 3, 4
3: 1
4: 1, 3
1 2 3 4
1 0 1 0 1
2 1 0 1 1
3 1 0 0 0
4 1 0 1 0

Adjacency Lists: Critique
• Advantages:
– Much more compact representation
– Easy to compute over outlinks
• Disadvantages:
– Much more difficult to compute over inlinks

Single Source Shortest Path
• Problem: find shortest path from a source
node to one or more target nodes
– Shortest might also mean lowest weight or cost
• First, a refresher: Dijkstra’s Algorithm

Dijkstra’s Algorithm Example
0




10
5
2 3
2
1
9
7
4 6
Example from CLR

0
10
5


Example from CLR
10
5
2 3
2
1
9
7
4 6

0
8
5
14
7
Example from CLR
10
5
2 3
2
1
9
7
4 6

0
8
5
13
7
Example from CLR
10
5
2 3
2
1
9
7
4 6

0
8
5
9
7
1
Example from CLR
10
5
2 3
2
1
9
7
4 6

0
8
5
9
7
Example from CLR
10
5
2 3
2
1
9
7
4 6

Single Source Shortest Path
• Problem: find shortest path from a source
node to one or more target nodes
– Shortest might also mean lowest weight or cost
• Single processor machine: Dijkstra’s Algorithm
• MapReduce: parallel Breadth-First Search
(BFS)

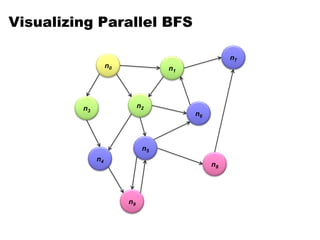
Finding the Shortest Path
 Consider simple case of equal edge weights
 Solution to the problem can be defined inductively
 Here’s the intuition:
 Define: b is reachable from a if b is on adjacency list of a
 DISTANCETO(s) = 0
 For all nodes p reachable from s,
DISTANCETO(p) = 1
 For all nodes n reachable from some other set of nodes M,
DISTANCETO(n) = 1 + min(DISTANCETO(m), m  M)
s
m3
m2
m1
n
…
…
…
d1
d2
d3

Visualizing Parallel BFS
n0
n3
n2
n1
n7
n6
n5
n4
n9
n8

From Intuition to Algorithm
• Data representation:
– Key: node n
– Value: d (distance from start), adjacency list (list of nodes
reachable from n)
– Initialization: for all nodes except for start node, d = 
• Mapper:
– m  adjacency list: emit (m, d + 1)
• Sort/Shuffle
– Groups distances by reachable nodes
• Reducer:
– Selects minimum distance path for each reachable node
– Additional bookkeeping needed to keep track of actual path

Multiple Iterations Needed
• Each MapReduce iteration advances the
“known frontier” by one hop
– Subsequent iterations include more and more
reachable nodes as frontier expands
– Multiple iterations are needed to explore entire
graph
• Preserving graph structure:
– Problem: Where did the adjacency list go?
– Solution: mapper emits (n, adjacency list) as well

Stopping Criterion
• How many iterations are needed in parallel
BFS (equal edge weight case)?
• Convince yourself: when a node is first
“discovered”, we’ve found the shortest path
• Now answer the question...
– Six degrees of separation?
• Practicalities of implementation in
MapReduce

Comparison to Dijkstra
• Dijkstra’s algorithm is more efficient
– At any step it only pursues edges from the
minimum-cost path inside the frontier
• MapReduce explores all paths in parallel
– Lots of “waste”
– Useful work is only done at the “frontier”
• Why can’t we do better using MapReduce?

Weighted Edges
• Now add positive weights to the edges
– Why can’t edge weights be negative?
• Simple change: adjacency list now includes a
weight w for each edge
– In mapper, emit (m, d + wp) instead of (m, d + 1)
for each node m
• That’s it?

Stopping Criterion
BFS (positive edge weight case)?
• Convince yourself: when a node is first
“discovered”, we’ve found the shortest path

Additional Complexities
s
p
q
r
search frontier
10
n1
n2
n3
n4
n5
n6 n7
n8
n9
1
1
1
1
1
1
1
1

Stopping Criterion
BFS (positive edge weight case)?
• Practicalities of implementation in
MapReduce

Graphs and MapReduce
• Graph algorithms typically involve:
– Performing computations at each node: based on node
features, edge features, and local link structure
– Propagating computations: “traversing” the graph
• Generic recipe:
– Represent graphs as adjacency lists
– Perform local computations in mapper
– Pass along partial results via outlinks, keyed by destination
node
– Perform aggregation in reducer on inlinks to a node
– Iterate until convergence: controlled by external “driver”
– Don’t forget to pass the graph structure between iterations

http://famousphil.com/blog/2011/06/a-hadoop-mapreduce-solution-to-dijkstra%E2%80%99s-algo
public class Dijkstra extends Configured implements Tool {
public static String OUT = "outfile";
public static String IN = "inputlarger”;
public static class TheMapper extends Mapper<LongWritable, Text, LongWritable, Text> {
public void map(LongWritable key, Text value, Context context) throws IOException,
InterruptedException {
Text word = new Text();
String line = value.toString();//looks like 1 0 2:3:
String[] sp = line.split(" ");//splits on space
int distanceadd = Integer.parseInt(sp[1]) + 1;
String[] PointsTo = sp[2].split(":");
for(int i=0; i<PointsTo.length; i++){
word.set("VALUE "+distanceadd);//tells me to look at distance value
context.write(new LongWritable(Integer.parseInt(PointsTo[i])), word);
word.clear(); }
//pass in current node's distance (if it is the lowest distance)
word.set("VALUE "+sp[1]);
context.write( new LongWritable( Integer.parseInt( sp[0] ) ), word );
word.clear();
word.set("NODES "+sp[2]);//tells me to append on the final tally
context.write( new LongWritable( Integer.parseInt( sp[0] ) ), word );
word.clear();
}

public static class TheReducer extends Reducer<LongWritable, Text, LongWritable,
Text> {
public void reduce(LongWritable key, Iterable<Text> values, Context context)
throws IOException, InterruptedException {
String nodes = "UNMODED";
Text word = new Text();
int lowest = 10009;//start at infinity
for (Text val : values) {//looks like NODES/VALUES 1 0 2:3:, we need to use
the first as a key
String[] sp = val.toString().split(" ");//splits on space
//look at first value
if(sp[0].equalsIgnoreCase("NODES")){
nodes = null;
nodes = sp[1];
}else if(sp[0].equalsIgnoreCase("VALUE")){
int distance = Integer.parseInt(sp[1]);
lowest = Math.min(distance, lowest);
}
}
word.set(lowest+" "+nodes);
context.write(key, word);
word.clear();
}
}

public int run(String[] args) throws Exception {
//http://code.google.com/p/joycrawler/source/browse/NetflixChallenge/src/org/niubility/learning/knn/KNND
va?r=242
getConf().set("mapred.textoutputformat.separator", " ");//make the key -> value space separated (for iter
…..
while(isdone == false){
Job job = new Job(getConf());
job.setJarByClass(Dijkstra.class);
job.setJobName("Dijkstra");
job.setOutputKeyClass(LongWritable.class);
job.setOutputValueClass(Text.class);
job.setMapperClass(TheMapper.class);
job.setReducerClass(TheReducer.class);
job.setInputFormatClass(TextInputFormat.class);
job.setOutputFormatClass(TextOutputFormat.class);
FileInputFormat.addInputPath(job, new Path(infile));
FileOutputFormat.setOutputPath(job, new Path(outputfile));
success = job.waitForCompletion(true);
//remove the input file
//http://eclipse.sys-con.com/node/1287801/mobile
if(infile != IN){
String indir = infile.replace("part-r-00000", "");
Path ddir = new Path(indir);
FileSystem dfs = FileSystem.get(getConf());
dfs.delete(ddir, true);
}

Random Walks Over the Web
• Random surfer model:
– User starts at a random Web page
– User randomly clicks on links, surfing from page to page
• PageRank
– Characterizes the amount of time spent on any given page
– Mathematically, a probability distribution over pages
• PageRank captures notions of page importance
– Correspondence to human intuition?
– One of thousands of features used in web search
– Note: query-independent

Given page x with inlinks t1…tn, where
 C(t) is the out-degree of t
  is probability of random jump
 N is the total number of nodes in the graph
PageRank: Defined











n
i i
i
t
C
t
PR
N
x
PR
1 )
(
)
(
)
1
(
1
)
( 

X
t1
t2
tn
…

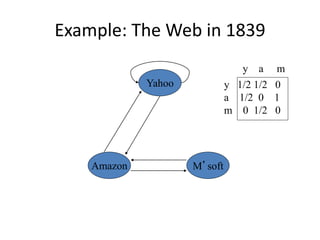
Example: The Web in 1839
Yahoo
M’soft
Amazon
y 1/2 1/2 0
a 1/2 0 1
m 0 1/2 0
y a m

Simulating a Random Walk
• Start with the vector v = [1,1,…,1]
representing the idea that each Web page is
given one unit of importance.
• Repeatedly apply the matrix M to v, allowing
the importance to flow like a random walk.
• Limit exists, but about 50 iterations is
sufficient to estimate final distribution.

Example
• Equations v = M v :
y = y /2 + a /2
a = y /2 + m
m = a /2
y
a =
m
1
1
1
1
3/2
1/2
5/4
1
3/4
9/8
11/8
1/2
6/5
6/5
3/5
. . .

Solving The Equations
• Because there are no constant terms, these 3
equations in 3 unknowns do not have a
unique solution.
• Add in the fact that y +a +m = 3 to solve.
• In Web-sized examples, we cannot solve by
Gaussian elimination; we need to use
relaxation (= iterative solution).

Real-World Problems
• Some pages are “dead ends” (have no links
out).
– Such a page causes importance to leak out.
• Other (groups of) pages are spider traps (all
out-links are within the group).
– Eventually spider traps absorb all importance.

Microsoft Becomes Dead End
Yahoo
M’soft
Amazon
y 1/2 1/2 0
a 1/2 0 0
m 0 1/2 0
y a m

Example
y = y /2 + a /2
a = y /2
m = a /2
y
a =
m
1
1
1
1
1/2
1/2
3/4
1/2
1/4
5/8
3/8
1/4
0
0
0
. . .

M’soft Becomes Spider Trap
Yahoo
M’soft
Amazon
y 1/2 1/2 0
a 1/2 0 0
m 0 1/2 1
y a m

Example
y = y /2 + a /2
a = y /2
m = a /2 + m
y
a =
m
1
1
1
1
1/2
3/2
3/4
1/2
7/4
5/8
3/8
2
0
0
3
. . .

Google Solution to Traps, Etc.
• “Tax” each page a fixed percentage at each
interation.
• Add the same constant to all pages.
• Models a random walk with a fixed probability
of going to a random place next.

Example: Previous with 20% Tax
• Equations v = 0.8(M v ) + 0.2:
y = 0.8(y /2 + a/2) + 0.2
a = 0.8(y /2) + 0.2
m = 0.8(a /2 + m) + 0.2
y
a =
m
1
1
1
1.00
0.60
1.40
0.84
0.60
1.56
0.776
0.536
1.688
7/11
5/11
21/11
. . .

Computing PageRank
• Properties of PageRank
– Can be computed iteratively
– Effects at each iteration are local
• Sketch of algorithm:
– Start with seed PRi values
– Each page distributes PRi “credit” to all pages it links
to
– Each target page adds up “credit” from multiple in-
bound links to compute PRi+1
– Iterate until values converge

Sample PageRank Iteration (1)
n1 (0.2)
n4 (0.2)
n3 (0.2)
n5 (0.2)
n2 (0.2)
0.1
0.1
0.2 0.2
0.1
0.1
0.066 0.066
0.066
n1 (0.066)
n4 (0.3)
n3 (0.166)
n5 (0.3)
n2 (0.166)
Iteration 1

Sample PageRank Iteration (2)
n1 (0.066)
n4 (0.3)
n3 (0.166)
n5 (0.3)
n2 (0.166)
0.033
0.033
0.3 0.166
0.083
0.083
0.1 0.1
0.1
n1 (0.1)
n4 (0.2)
n3 (0.183)
n5 (0.383)
n2 (0.133)
Iteration 2

PageRank in MapReduce
n5 [n1, n2, n3]
n1 [n2, n4] n2 [n3, n5] n3 [n4] n4 [n5]
n2 n4 n3 n5 n1 n2 n3
n4 n5
n2 n4
n3 n5
n1 n2 n3 n4 n5
n5 [n1, n2, n3]
n1 [n2, n4] n2 [n3, n5] n3 [n4] n4 [n5]
Map
Reduce

Complete PageRank
• Two additional complexities
– What is the proper treatment of dangling nodes?
– How do we factor in the random jump factor?
• Solution:
– Second pass to redistribute “missing PageRank mass” and
account for random jumps
– p is PageRank value from before, p' is updated PageRank
value
– |G| is the number of nodes in the graph
– m is the missing PageRank mass



















 p
G
m
G
p )
1
(
1
' 


PageRank Convergence
• Alternative convergence criteria
– Iterate until PageRank values don’t change
– Iterate until PageRank rankings don’t change
– Fixed number of iterations
• Convergence for web graphs?

Beyond PageRank
• Link structure is important for web search
– PageRank is one of many link-based features: HITS,
SALSA, etc.
– One of many thousands of features used in ranking…
• Adversarial nature of web search
– Link spamming
– Spider traps
– Keyword stuffing
– …

Efficient Graph Algorithms
• Sparse vs. dense graphs
• Graph topologies

Figure from: Newman, M. E. J. (2005) “Power laws, Pareto distributions and
Zipf's law.” Contemporary Physics 46:323–351.

Local Aggregation
• Use combiners!
– In-mapper combining design pattern also
applicable
• Maximize opportunities for local aggregation
– Simple tricks: sorting the dataset in specific ways

Graph Algorithms - Map-Reduce Graph Processing

Recommended

More Related Content

Similar to Graph Algorithms - Map-Reduce Graph Processing (20)

More from Jason J Pulikkottil (20)

Recently uploaded (20)

Graph Algorithms - Map-Reduce Graph Processing