Greedy technique - Algorithm design techniques using data structures

• A greedy algorithm is an approach for solving a problem by
selecting the best option available at the moment, without
worrying about the future result it would bring.
• In other words, the locally best choices aim at producing
globally best results.

Advantages
1.The algorithm is easier to describe.
2.This algorithm can perform better than other algorithms
(but, not in all cases).

Greedy Algorithm
1.To begin with, the solution set (containing answers) is
empty.
2.At each step, an item is added into the solution set.
3.If the solution set is feasible, the current item is kept.
4.Else, the item is rejected and never considered again.

Basic Concepts
Spanning Trees: A subgraph T of a undirected graph G = ( V, E ) is a
spanning tree of G if it is a tree and contains every vertex of G.
a
b
c
d
e
a
b
c
d
e
a
b
c
d
e
a
b
c
e
d
Graph
Spanning Tree 1 Spanning Tree 2 Spanning Tree 3
• Every connected graph has a spanning tree.
• May have multiple spanning tree.
• For example see this graph.

Basic Concepts Cont…..
Weighted Graph: A weighted graph is a graph, in which each edge has
a weight (some real number ) Example:
a
b
c
10
9
e
d
Weighted Graph
7 32
23

Basic Concepts Cont….
Minimum Spanning Tree in an undirected connected weighted graph is
a spanning tree of minimum weight. Example:
b
c
10
9
e
d
Weighted Graph
a 7 32
23
a
c
d
Spanning Tree 1,
w=74
10
9 e
32
23
a
c
d
w=71
9 e
7 32
23
b b a
c
e
d
Spanning Tree 3,
w=72
7 32
10 23
b
Spanning Tree 2,
(Minimum Spanning Tree)

Minimum Spanning Tree Problem
MST Problem : Given a connected weighted undirected graph G,
design an algorithm that outputs a minimum spanning tree (MST) of
graph G.
• How to find Minimum Spanning Tree ?
• Generic solution to MST
Two
Algorithms
Kruskal’s
algorithm
Prim’s
algorithm

Applications of Minimum Spanning Tree
1.Consider n stations are to be linked using a communication network
& laying of communication links between any two stations involves a
cost.
The ideal solution would be to extract a subgraph termed as
minimum cost spanning tree.
2.Suppose you want to construct highways or railroads spanning
several cities then we can use the concept of minimum spanning
trees.
3.Designing Local Area Networks.
4.Laying pipelines connecting offshore drilling sites, refineries and
consumer markets.
5.Suppose you want to apply a set of houses with
1. Electric Power
2. Water
3. Telephone lines
4. Sewage lines
To reduce cost, you can connect houses with minimum cost spanning
trees.

Kruskal’s Algorithm
• The set of edges (T) is initially empty.
• As the algorithm progresses, edges are added to T at every
instance.
• The partial graph formed by the nodes of G, and the edges in
T consists of several connected components.
• At the end of the algorithm, only the connected component
remains, so that T is then a minimum spanning tree of all
nodes of G.

The steps for implementing Kruskal's
algorithm are as follows:
1.Sort all the edges from low weight to high
2.Take the edge with the lowest weight and add it
to the spanning tree. If adding the edge created
a cycle, then reject this edge.
3.Keep adding edges until we reach all vertices.

• First step to solve is to arrange the edges in the increasing order of
their costs.

Edge Cost
1 - 2 5
1 - 3 10
2 – 6 20
3 - 6 25
4 - 5 35
2 - 4 45
5 - 6 45
4 - 6 50
2 - 5 55

• Next step is to create the following table

Step Edge Considered Connected
component
Graph
Initial - [1] [2] [3] [4] [5] [6] -
1. [1 – 2] [12] [3] [4] [5] [6]
Accepted because
no cycle
2. [1 – 3] [1 2 3] [4] [5] [6]
Accepted because
no cycle
1 2
5
1 2
3
5
10

Component
Graph
3. [2 – 6] [1 2 3 6] [4] [5]
Accepted because
no cycle
4. [3 – 6] Rejected because it
forms a cycle
-
5. [4 – 5] [1 2 3 6] [4 5]
Accepted because
no cycle
1 2
3
6
5
10
20
1 2
3
4 5
5
10 20 35

Component
Graph
6. [2 – 4] [1 2 3 4 5 6]
Accepted because no
cycle
7. [5 – 6] rejected -
8. [4 – 6] rejected
5
10
20
45
35

Step Edge
Considered
Connected
Component
Graph
8. [4 - 6] Rejected -
9. [2 – 5] Rejected -

Algorithm Kruskal(T,E,n)
• T is the spanning tree, E is the list of edges, n is the number of nodes in given graph G
{
initially T=0;
while ( T <> n-1 and E <> 0 )
{
find the min-cost edge in E and call it as (U,V)
if (U,V) does not form a cycle
T = T + (U,V)
else
delete(U,V);
}
if ( |T| = n-1 )
display “Spanning Tree,T”
else
display “No Spanning Tree”
}

Dijkstra’s Algorithm
• Given a graph and a source vertex in the graph, find the
shortest paths from the source to all vertices in the given
graph.
• Dijkstra's Algorithm works on the basis that any sub path B -> D of
the shortest path A -> D between vertices A and D is also the
shortest path between vertices B and D.
• Djikstra used this property in the opposite direction i.e we
overestimate the distance of each vertex from the starting vertex.
Then we visit each node and its neighbors to find the shortest sub
path to those neighbors.

function dijkstra(G, S)
for each vertex V in G
distance[V] <- infinite
previous[V] <- NULL
If V != S, add V to Priority Queue Q
distance[S] <- 0
while Q IS NOT EMPTY
U <- Extract MIN from Q
for each unvisited neighbour V of U
tempDistance <- distance[U] + edge_weight(U, V)
if tempDistance < distance[V]
distance[V] <- tempDistance
previous[V] <- U
return distance[], previous[]

Greedy technique - Algorithm design techniques using data structures

Dijkstra's Algorithm Complexity
• Time Complexity: O(E Log V)
• where, E is the number of edges and V is the number of vertices.
• Space Complexity: O(V)
Dijkstra's Algorithm Applications
• To find the shortest path
• In social networking applications
• In a telephone network
• To find the locations in the map

Prim’s Algorithm
• The algorithm starts with an empty spanning tree. The idea is to
maintain two sets of vertices.
• The first set contains the vertices already included in the MST,
and the other set contains the vertices not yet included.
• At every step, it considers all the edges that connect the two sets
and picks the minimum weight edge from these edges.
• After picking the edge, it moves the other endpoint of the edge
to the set containing MST.

• Step 1: Firstly, we select an arbitrary vertex that acts as the
starting vertex of the Minimum Spanning Tree. Here we have
selected vertex 0 as the starting vertex.

• Step 2: All the edges connecting the incomplete MST and other
vertices are the edges {0, 1} and {0, 7}. Between these two the
edge with minimum weight is {0, 1}. So include the edge and
vertex 1 in the MST.

• Step 3: The edges connecting the incomplete MST to other
vertices are {0, 7}, {1, 7} and {1, 2}. Among these edges the
minimum weight is 8 which is of the edges {0, 7} and {1, 2}. Let
us here include the edge {0, 7} and the vertex 7 in the MST. [We
could have also included edge {1, 2} and vertex 2 in the MST].

• Step 4: The edges that connect the incomplete MST with the
fringe vertices are {1, 2}, {7, 6} and {7, 8}. Add the edge {7, 6}
and the vertex 6 in the MST as it has the least weight (i.e., 1).

• Step 5: The connecting edges now are {7, 8}, {1, 2}, {6, 8} and
{6, 5}. Include edge {6, 5} and vertex 5 in the MST as the edge
has the minimum weight (i.e., 2) among them.

• Step 6: Among the current connecting edges, the edge {5, 2}
has the minimum weight. So include that edge and the vertex 2
in the MST.

• Step 7: The connecting edges between the incomplete MST and
the other edges are {2, 8}, {2, 3}, {5, 3} and {5, 4}. The edge with
minimum weight is edge {2, 8} which has weight 2. So include
this edge and the vertex 8 in the MST.

• Step 8: See here that the edges {7, 8} and {2, 3} both have same
weight which are minimum. But 7 is already part of MST. So we
will consider the edge {2, 3} and include that edge and vertex 3
in the MST.

• Step 9: Only the vertex 4 remains to be included. The minimum
weighted edge from the incomplete MST to 4 is {3, 4}.

• The final structure of the MST is as follows and the weight of the
edges of the MST is (4 + 8 + 1 + 2 + 4 + 2 + 7 + 9) = 37.

Huffman coding
• Huffman coding is a lossless data compression algorithm.
The idea is to assign variable-length codes to input
characters, lengths of the assigned codes are based on the
frequencies of corresponding characters.
• There are mainly two major parts in Huffman Coding
1.Build a Huffman Tree from input characters.
2.Traverse the Huffman Tree and assign codes to characters

• Steps to build Huffman Tree
Input is an array of unique characters along with their frequency of occurrences
and output is Huffman Tree.
1.Create a leaf node for each unique character and build a min heap of all leaf nodes
(Min Heap is used as a priority queue. The value of frequency field is used to
compare two nodes in min heap. Initially, the least frequent character is at root)
2.Extract two nodes with the minimum frequency from the min heap.
3.Create a new internal node with a frequency equal to the sum of the two nodes
frequencies. Make the first extracted node as its left child and the other extracted
node as its right child. Add this node to the min heap.
4.Repeat steps#2 and #3 until the heap contains only one node. The remaining node
is the root node and the tree is complete.

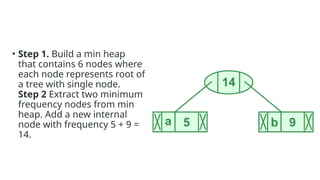
• Step 1. Build a min heap
that contains 6 nodes where
each node represents root of
a tree with single node.
Step 2 Extract two minimum
frequency nodes from min
heap. Add a new internal
node with frequency 5 + 9 =
14.

• Now min heap contains 5 nodes where 4 nodes are roots of
trees with single element each, and one heap node is root of
tree with 3 elements

• Step 3: Extract two minimum frequency nodes from heap.
Add a new internal node with frequency 12 + 13 = 25

• Now min heap contains 4 nodes where 2 nodes are roots of
trees with single element each, and two heap nodes are root
of tree with more than one nodes

• Step 4: Extract two minimum frequency nodes. Add a new
internal node with frequency 14 + 16 = 30

• Now min heap contains 3 nodes.

• Now min heap contains 2 nodes.

• Now min heap contains only one node.
• Since the heap contains only one node, the algorithm stops
here.

• Steps to print codes from Huffman Tree:
Traverse the tree formed starting from the root. Maintain an
auxiliary array. While moving to the left child, write 0 to the
array. While moving to the right child, write 1 to the array.
Print the array when a leaf node is encountered.

Greedy technique - Algorithm design techniques using data structures

Recommended

More Related Content

Similar to Greedy technique - Algorithm design techniques using data structures (20)

More from divyammo (8)

Recently uploaded (20)

Greedy technique - Algorithm design techniques using data structures