![Branch-and-Bound Method
Harrison Electric Company Revisited
If you solve both sub-problems graphically
[X1 = 4, X2 = 1.2, profit = $35.20]
Sub-problem A’s optimal
solution:
Sub-problem B’s optimal
solution: [X1 = 3, X2 = 2, profit = $33.00]
We have completed steps 1 to 4 of the branch-and-bound method.](https://image.slidesharecdn.com/integerprogramming-goalprogramming-160916022303/85/Integer-Programming-Goal-Programming-and-Nonlinear-Programming-31-320.jpg)
Integer Programming, Goal Programming, and Nonlinear Programming
- 1. Chapter 11 Integer Programming, Goal Programming, and Nonlinear Programming. Prepared By: Salah A. Skaik
- 2. In this Chapter: • Integer Programming. • Goal Programming. • Nonlinear Programming.
- 3. Integer Programming IP is the extension of LP that solves problems requiring Integer Solutions. Ex. (Airline) There are two ways to solve IP Problems: 1- Graphically. 2- The Branch & Bound Method.
- 4. Goal Programming GP is the extension of LP that permits Multiple Objectives to be stated. Ex. (Max profit & Max market share).
- 5. Nonlinear Programming NLP is the case in which Objectives or Constraints are Nonlinear. Ex. (Maximizing profit = 25X1 - 0.4X²1 + 30X2 – 0.5X²2 ). Ex. (12X1 - 0.6X²1 ≥ 3,500 ).
- 6. Integer Programming • There are three types of Integer Programs: 1- Pure Integer Programs. 2- Mixed-Integer Programs. 3- Zero-One Integer Programming. (special cases).
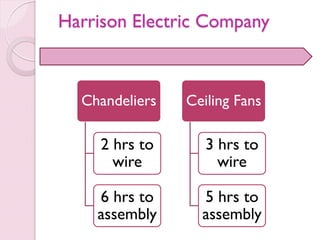
- 7. Example of Integer Programming Harrison Electric Company
- 8. Harrison Electric Company Chandeliers 2 hrs to wire 6 hrs to assembly Ceiling Fans 3 hrs to wire 5 hrs to assembly
- 9. • 12 hrs of wiring • 30 hrs of assembly Production Capability • 7$ each chandelier • 6$ each fanNet Profit Harrison Electric Company
- 10. Harrison Electric Company Let: X1 = Number of chandeliers produced. X2 = Number of ceiling fans produced.
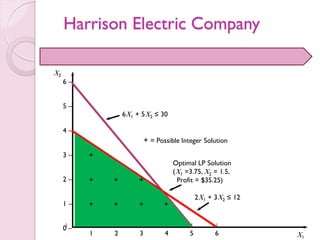
- 11. Harrison Electric Company Objective Function: Maximize Profit = $7 X1 + $6 X2 Subject to: 2X1 + 3X2 ≤ 12 (wiring hours) 6X1 + 5X2 ≤ 30 (assembly hours)
- 12. 6 – 5 – 4 – 3 – 2 – 1 – 0 – | | | | | | | 1 2 3 4 5 6 X1 X2 + ++ ++++ + 6X1 + 5X2 ≤ 30 2X1 + 3X2 ≤ 12 + = Possible Integer Solution Optimal LP Solution (X1 =3.75, X2 = 1.5, Profit = $35.25) Harrison Electric Company
- 13. In case the company doesn’t produce a fraction of the product: 1- Rounding Off. 2- Enumeration Method. Harrison Electric Company
- 14. Rounding Off has two problems: 1- Integer solution may not be in feasible region. (X1=4, X2=2). (unpractical solution) 2- May not be the optimal feasible Integer solution. (X1=4, X2=1). Harrison Electric Company
- 15. Enumeration Method Harrison Electric Company
- 16. Optimal solution to integer programming problem Solution if rounding is used CHANDELIERS (X1) CEILING FANS (X2) PROFIT ($7X1 + $6X2) 0 0 $0 1 0 7 2 0 14 3 0 21 4 0 28 5 0 35 0 1 6 1 1 13 2 1 20 3 1 27 4 1 34 0 2 12 1 2 19 2 2 26 3 2 33 0 3 18 1 3 25 0 4 24 Harrison Electric Company
- 17. An integer solution can never be better than the LP solution and is usually a lesser solution. Harrison Electric Company
- 18. Six Steps in Solving IP Maximization Problems by Branch and Bound Branch-and-Bound Method
- 19. Step(1): Solve the original problem using LP. If the answer satisfies the integer constraints, we are done. If not, this value provides an initial upper bound. Branch-and-Bound Method
- 20. Step(2): Find any feasible solution that meets the integer constraints for use as a lower bound. Usually, rounding down each variable will accomplish this. Branch-and-Bound Method
- 21. Step(3): Branch on one variable from step 1 that does not have an integer value. Split the problem into two sub-problems based on integer values that are immediately above or below the non-Integer value. Branch-and-Bound Method
- 22. Step(4): Create nodes at the top of these new branches by solving the new problem. Branch-and-Bound Method
- 23. Step(5-a): If a branch yields a solution to the LP problem that is not feasible, terminate the branch. Branch-and-Bound Method
- 24. Step(5-b): If a branch yields a solution to the LP problem that is feasible, but not an integer solution, go to step 6. Branch-and-Bound Method
- 25. Step(5-c): If the branch yields a feasible integer solution, examine the value of the objective function. If this value equals the upper bound, an optimal solution has been reached. If it not equal to the upper bound, but exceeds the lower bound, set it as the new lower bound and go to step 6. finally, if it’s less than the lower bound terminate this branch. Branch-and-Bound Method
- 26. Step(6): Examine both branches again and set the upper bound equal to the maximum value of the objective function at all final nodes. If the upper bound equals the lower bound, stop. If not, go back to step 3. Branch-and-Bound Method
- 27. NOTE: Minimization problems involved reversing the roles of the upper and lower bounds. Branch-and-Bound Method
- 28. Branch-and-Bound Method Harrison Electric Company Revisited Recall that the Harrison Electric Company’s integer programming formulation is Maximize profit = $7X1 + $6X2 subject to 2X1 + 3X2 ≤ 12 6X1 + 5X2 ≤ 30 where X1 = number of chandeliers produced X2 = number of ceiling fans produced And the optimal non-integer solution is X1 = 3.75 chandeliers, X2 = 1.5 ceiling fans profit = $35.25
- 29. Branch-and-Bound Method Harrison Electric Company Revisited Since X1 and X2 are not integers, this solution is not valid. The profit value of $35.25 will provide the initial upper bound. We can round down to X1 = 3, X2 = 1, profit = $27, which provides a feasible lower bound. The problem is now divided into two sub-problems.
- 30. Branch-and-Bound Method Harrison Electric Company Revisited Maximize profit = $7X1 + $6X2 subject to 2X1 + 3X2 ≤ 12 6X1 + 5X2 ≤ 30 X1 ≥ 4 Subproblem A Maximize profit = $7X1 + $6X2 subject to 2X1 + 3X2 ≤ 12 6X1 + 5X2 ≤ 30 X1 ≤ 3 Subproblem B
- 31. Branch-and-Bound Method Harrison Electric Company Revisited If you solve both sub-problems graphically [X1 = 4, X2 = 1.2, profit = $35.20] Sub-problem A’s optimal solution: Sub-problem B’s optimal solution: [X1 = 3, X2 = 2, profit = $33.00] We have completed steps 1 to 4 of the branch-and-bound method.
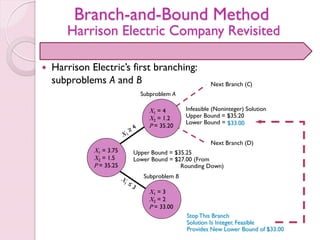
- 32. Branch-and-Bound Method Harrison Electric Company Revisited Harrison Electric’s first branching: subproblems A and B Subproblem A Next Branch (C) Next Branch (D) Upper Bound = $35.25 Lower Bound = $27.00 (From Rounding Down) X1 = 4 X2 = 1.2 P = 35.20 X1 = 3 X2 = 2 P = 33.00 StopThis Branch Solution Is Integer, Feasible Provides New Lower Bound of $33.00 X1 = 3.75 X2 = 1.5 P = 35.25 Infeasible (Noninteger) Solution Upper Bound = $35.20 Lower Bound = $33.00 Subproblem B
- 33. Branch-and-Bound Method Harrison Electric Company Revisited Maximize profit = $7X1 + $6X2 subject to 2X1 + 3X2 ≤ 12 6X1 + 5X2 ≤ 30 X1 ≥ 4 X2 ≥ 2 Subproblem C Maximize profit = $7X1 + $6X2 subject to 2X1 + 3X2 ≤ 12 6X1 + 5X2 ≤ 30 X1 ≥ 4 X2 ≤ 1 Subproblem D Subproblem A has branched into two new subproblems, C and D.
- 34. Branch-and-Bound Method Harrison Electric Company Revisited Subproblem C has no feasible solution because the all the constraints can not be satisfied We terminate this branch and do not consider this solution Subproblem D’s optimal solution is X1 = 4.17, X2 = 1, profit = $35.16 This noninteger solution yields a new upper bound of $35.16
- 35. Branch-and-Bound Method Harrison Electric Company Revisited Maximize profit = $7X1 + $6X2 subject to 2X1 + 3X2 ≤ 12 6X1 + 5X2 ≤ 30 X1 ≥ 4 X1 ≤ 4 X2 ≤ 1 Subproblem E Maximize profit = $7X1 + $6X2 subject to 2X1 + 3X2 ≤ 12 6X1 + 5X2 ≤ 30 X1 ≥ 4 X1 ≥ 5 X2 ≤ 1 Subproblem D Finally we create subproblems E and F Optimal solution to E: X1 = 4, X2 = 1, profit = $34 Optimal solution to F: X1 = 5, X2 = 0, profit = $35
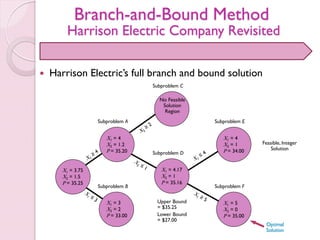
- 36. Branch-and-Bound Method Harrison Electric Company Revisited Subproblem F X1 = 5 X2 = 0 P = 35.00 Subproblem E X1 = 4 X2 = 1 P = 34.00 Harrison Electric’s full branch and bound solution Feasible, Integer Solution Optimal Solution Upper Bound = $35.25 Lower Bound = $27.00 Subproblem C No Feasible Solution Region Subproblem D X1 = 4.17 X2 = 1 P = 35.16 Subproblem A X1 = 4 X2 = 1.2 P = 35.20 Subproblem B X1 = 3 X2 = 2 P = 33.00 X1 = 3.75 X2 = 1.5 P = 35.25
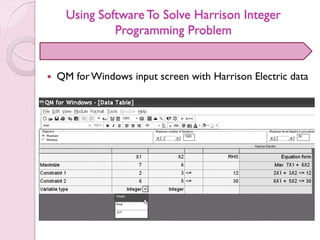
- 37. Using Software To Solve Harrison Integer Programming Problem QM forWindows input screen with Harrison Electric data
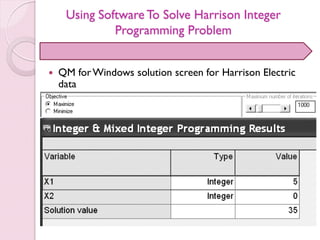
- 38. Using Software To Solve Harrison Integer Programming Problem QM forWindows solution screen for Harrison Electric data
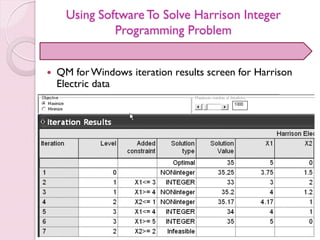
- 39. Using Software To Solve Harrison Integer Programming Problem QM forWindows iteration results screen for Harrison Electric data
- 40. Using Software To Solve Harrison Integer Programming Problem Using Excel’s Solver to formulate Harrison’s integer programming model
- 41. Using Software To Solve Harrison Integer Programming Problem Integer variables are specified with a drop-down menu in Solver
- 42. Using Software To Solve Harrison Integer Programming Problem Excel solution to the Harrison Electric integer programming model
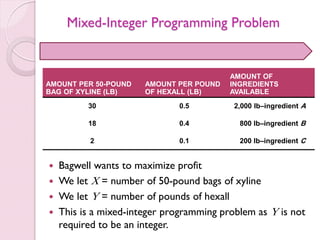
- 43. Mixed-Integer Programming Problem There are many situations in which some of the variables are restricted to be integers and some are not.
- 44. Mixed-Integer Programming Problem Bagwell wants to maximize profit We let X = number of 50-pound bags of xyline We let Y = number of pounds of hexall This is a mixed-integer programming problem as Y is not required to be an integer. AMOUNT PER 50-POUND BAG OF XYLINE (LB) AMOUNT PER POUND OF HEXALL (LB) AMOUNT OF INGREDIENTS AVAILABLE 30 0.5 2,000 lb–ingredient A 18 0.4 800 lb–ingredient B 2 0.1 200 lb–ingredient C
- 45. Mixed-Integer Programming Problem The model is Maximize profit = $85X + $1.50Y subject to 30X + 0.5Y ≤ 2,000 18X + 0.4Y ≤ 800 2X + 0.1Y ≤ 200 X, Y ≥ 0 and X integer
- 46. Mixed-Integer Programming Problem Using QM forWindows and Excel to solve Bagwell’s IP model
- 47. Mixed-Integer Programming Problem Excel formulation of Bagwell’s IP problem with Solver
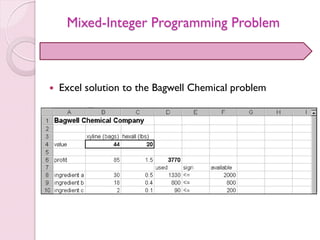
- 48. Mixed-Integer Programming Problem Excel solution to the Bagwell Chemical problem
- 49. ModelingWith 0-1 (Binary)Variables We can demonstrate how 0-1 variables can be used to model several diverse situations. Typically a 0-1 variable is assigned a value of 0 if a certain condition is not met and a 1 if the condition is met. This is also called a binary variable
- 50. Capital Budgeting Example A common capital budgeting problem is selecting from a set of possible projects when budget limitations make it impossible to select them all A 0-1 variable is defined for each project Quemo Chemical Company is considering three possible improvement projects for its plant ◦ A new catalytic converter ◦ A new software program for controlling operations ◦ Expanding the storage warehouse It can not do them all They want to maximize net present value of projects undertaken
- 51. Capital Budgeting Example The basic model is Maximize net present value of projects undertaken subject to Total funds used in year 1 ≤ $20,000 Total funds used in year 2 ≤ $16,000 Quemo Chemical Company information PROJECT NET PRESENT VALUE YEAR 1 YEAR 2 Catalytic Converter $25,000 $8,000 $7,000 Software $18,000 $6,000 $4,000 Warehouse expansion $32,000 $12,000 $8,000 Available funds $20,000 $16,000
- 52. Capital Budgeting Example The mathematical statement of the integer programming problem becomes Maximize NPV = 25,000X1 + 18,000X2 + 32,000X3 subject to 8,000X1 + 6,000X2 + 12,000X3 ≤ 20,000 7,000X1 + 4,000X2 + 8,000X3 ≤ 16,000 X1, X2, X3 = 0 or 1 The decision variables are X1 = 1 if catalytic converter project is funded 0 otherwise X2 = 1 if software project is funded 0 otherwise X3 = 1 if warehouse expansion project is funded 0 otherwise
- 53. Capital Budgeting Example Solved with computer software, the optimal solution is X1 = 1, X2 = 0, and X3 = 1 with an objective function value of 57,000 This means that Quemo Chemical should fund the catalytic converter and warehouse expansion projects only The net present value of these investments will be $57,000
- 54. Limiting the Number of Alternatives Selected One common use of 0-1 variables involves limiting the number of projects or items that are selected from a group Suppose Quemo Chemical is required to select no more than two of the three projects regardless of the funds available This would require adding a constraint X1 + X2 + X3 ≤ 2 If they had to fund exactly two projects the constraint would be X1 + X2 + X3 = 2
- 55. Dependent Selections At times the selection of one project depends on the selection of another project Suppose Quemo’s catalytic converter could only be purchased if the software was purchased The following constrain would force this to occur X1 ≤ X2 or X1 – X2 ≤ 0 If we wished for the catalytic converter and software projects to either both be selected or both not be selected, the constraint would be X1 = X2 or X1 – X2 = 0
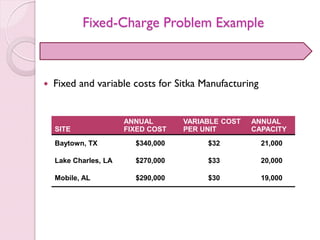
- 56. Fixed-Charge Problem Example Often businesses are faced with decisions involving a fixed charge that will affect the cost of future operations Sitka Manufacturing is planning to build at least one new plant and three cities are being considered in ◦ Baytown,Texas ◦ Lake Charles, Louisiana ◦ Mobile,Alabama Once the plant or plants are built, the company want to have capacity to produce at least 38,000 units each year
- 57. Fixed-Charge Problem Example Fixed and variable costs for Sitka Manufacturing SITE ANNUAL FIXED COST VARIABLE COST PER UNIT ANNUAL CAPACITY Baytown, TX $340,000 $32 21,000 Lake Charles, LA $270,000 $33 20,000 Mobile, AL $290,000 $30 19,000
- 58. Fixed-Charge Problem Example We can define the decision variables as X1 = 1 if factory is built in Baytown 0 otherwise X2 = 1 factory is built in Lake Charles 0 otherwise X3 = 1 if factory is built in Mobile 0 otherwise X4 = number of units produced at Baytown plant X5 = number of units produced at Lake Charles plant X6 = number of units produced at Mobile plant
- 59. Fixed-Charge Problem Example The integer programming formulation becomes Minimize cost = 340,000X1 + 270,000X2 + 290,000X3 + 32X4 + 33X5 + 30X6 subject to X4 + X5 + X6 ≥ 38,000 X4 ≤ 21,000X1 X5 ≤ 20,000X2 X6 ≤ 19,000X3 X1, X2, X3 = 0 or 1; X4, X5, X6 ≥ 0 and integer The optimal solution is X1 = 0, X2 = 1, X3 = 1, X4 = 0, X5 = 19,000, X6 = 19,000 Objective function value = $1,757,000
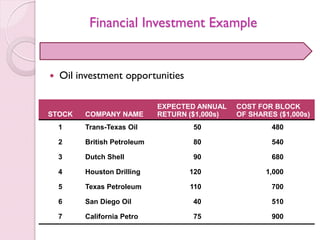
- 60. Financial Investment Example Numerous financial applications exist with 0-1 variables Simkin, Simkin, and Steinberg specialize in recommending oil stock portfolios for wealthy clients One client has the following specifications ◦ At least twoTexas firms must be in the portfolio ◦ No more than one investment can be made in a foreign oil company ◦ One of the two California oil stocks must be purchased The client has $3 million to invest and wants to buy large blocks of shares
- 61. Financial Investment Example Oil investment opportunities STOCK COMPANY NAME EXPECTED ANNUAL RETURN ($1,000s) COST FOR BLOCK OF SHARES ($1,000s) 1 Trans-Texas Oil 50 480 2 British Petroleum 80 540 3 Dutch Shell 90 680 4 Houston Drilling 120 1,000 5 Texas Petroleum 110 700 6 San Diego Oil 40 510 7 California Petro 75 900
- 62. Financial Investment Example Model formulation Maximize return = 50X1 + 80X2 + 90X3 + 120X4 + 110X5 + 40X6 + 75X7 subject to X1 + X4 + X5 ≥ 2 (Texas constraint) X2+ X3 ≤ 1 (foreign oil constraint) X6 + X7 = 1 (California constraint) 480X1 + 540X2 + 680X3 + 1,000X4 + 700X5 + 510X6 + 900X7 ≤ 3,000 ($3 million limit) All variables must be 0 or 1
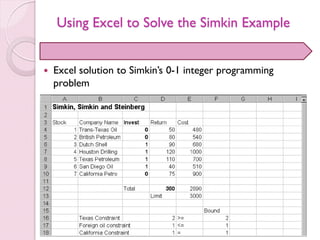
- 63. Using Excel to Solve the Simkin Example Solver input for Simkin’s 0-1 variables
- 64. Using Excel to Solve the Simkin Example Complete Solver input for Simkin’s 0-1 integer programming problem
- 65. Using Excel to Solve the Simkin Example Excel solution to Simkin’s 0-1 integer programming problem
- 66. Solved Problem 11-1 Consider the 0-1 integer programming problem that follows: Maximize = 50X1 + 45X2 + 48X3 Subject to: 19X1 + 27X2 + 34X3 ≤ 80 22X1 + 13X2 + 12X3 ≤ 40 X1, X2, X3 must be either 0 or 1
- 67. Solved Problem 11-1 Additional constraints: 1- No more than two of the three variables can take on a value equal to 1 in the solution. 2- Make sure that if X1 = 1, then X2 = 1 also.
- 68. Solved Problem 11-1 The model is Maximize = 50X1 + 45X2 + 48X3 Subject to: 19X1 + 27X2 + 34X3 ≤ 80 22X1 + 13X2 + 12X3 ≤ 40 X1 + X2 + X3 ≤ 2 X1 - X2 ≤ 0 X1, X2, X3 must be either 0 or 1