Learn data structures algorithms tutorial
- 2. Data Structures & Algorithms i AbouttheTutorial Data Structures are the programmatic way of storing data so that data can be used efficiently. Almost every enterprise application uses various types of data structures in one or the other way. This tutorial will give you a great understanding on Data Structures needed to understand the complexity of enterprise level applications and need of algorithms, and data structures. Audience This tutorial is designed for Computer Science graduates as well as Software Professionals who are willing to learn data structures and algorithm programming in simple and easy steps. After completing this tutorial you will be at intermediate level of expertise from where you can take yourself to higher level of expertise. Prerequisites Before proceeding with this tutorial, you should have a basic understanding of C programming language, text editor, and execution of programs, etc. CopyrightandDisclaimer © Copyright 2016 by Tutorials Point (I) Pvt. Ltd. All the content and graphics published in this e-book are the property of Tutorials Point (I) Pvt. Ltd. The user of this e-book is prohibited to reuse, retain, copy, distribute or republish any contents or a part of contents of this e-book in any manner without written consent of the publisher. We strive to update the contents of our website and tutorials as timely and as precisely as possible, however, the contents may contain inaccuracies or errors. Tutorials Point (I) Pvt. Ltd. provides no guarantee regarding the accuracy, timeliness or completeness of our website or its contents including this tutorial. If you discover any errors on our website or in this tutorial, please notify us at [email protected]
- 3. Data Structures & Algorithms ii Compile&ExecuteOnline For most of the examples given in this tutorial you will find Try it option, so just make use of this option to execute your programs on the spot and enjoy your learning. Try the following example using the Try it option available at the top right corner of the following sample code box − #include <stdio.h> int main(){ /* My first program in C */ printf("Hello, World! n"); return 0; }
- 4. Data Structures & Algorithms iii TableofContents About the Tutorial ............................................................................................................................................i Audience...........................................................................................................................................................i Prerequisites.....................................................................................................................................................i Copyright and Disclaimer .................................................................................................................................i Compile & Execute Online............................................................................................................................... ii Table of Contents ........................................................................................................................................... iii BASICS.........................................................................................................................................1 1. Overview ..................................................................................................................................................2 Characteristics of a Data Structure..................................................................................................................2 Need for Data Structure ..................................................................................................................................2 Execution Time Cases ......................................................................................................................................3 Basic Terminology ...........................................................................................................................................3 2. Environment Setup ...................................................................................................................................4 Try it Option Online.........................................................................................................................................4 Local Environment Setup.................................................................................................................................4 Installation on UNIX/Linux...............................................................................................................................5 Installation on Mac OS.....................................................................................................................................5 Installation on Windows..................................................................................................................................6 ALGORITHM................................................................................................................................7 3. Algorithms ─ Basics...................................................................................................................................8 Characteristics of an Algorithm .......................................................................................................................8 How to Write an Algorithm? ...........................................................................................................................9 Algorithm Analysis.........................................................................................................................................10 Algorithm Complexity....................................................................................................................................11 Space Complexity ..........................................................................................................................................11 Time Complexity............................................................................................................................................11 4. Asymptotic Analysis................................................................................................................................12 Asymptotic Notations....................................................................................................................................12 Common Asymptotic Notations ....................................................................................................................15 5. Greedy Algorithms..................................................................................................................................16 Counting Coins...............................................................................................................................................16 6. Divide & Conquer....................................................................................................................................18 Divide/Break..................................................................................................................................................18 Conquer/Solve...............................................................................................................................................18 Merge/Combine ............................................................................................................................................19 7. Dynamic Programming............................................................................................................................20
- 5. Data Structures & Algorithms iv DATA STRUCTURES ...................................................................................................................21 8. Basic Concepts ........................................................................................................................................22 Data Definition ..............................................................................................................................................22 Data Object....................................................................................................................................................22 Data Type.......................................................................................................................................................22 Basic Operations............................................................................................................................................23 9. Arrays .....................................................................................................................................................24 Array Representation ....................................................................................................................................24 Basic Operations............................................................................................................................................25 Insertion Operation .......................................................................................................................................25 Array Insertions .............................................................................................................................................27 Insertion at the Beginning of an Array ..........................................................................................................28 Insertion at the Given Index of an Array .......................................................................................................30 Insertion After the Given Index of an Array ..................................................................................................32 Insertion Before the Given Index of an Array................................................................................................34 Deletion Operation........................................................................................................................................36 Search Operation...........................................................................................................................................37 Update Operation..........................................................................................................................................39 LINKED LIST...............................................................................................................................41 10. Linked List ─ Basics..................................................................................................................................42 Linked List Representation ............................................................................................................................42 Types of Linked List .......................................................................................................................................42 Basic Operations............................................................................................................................................43 Insertion Operation .......................................................................................................................................43 Deletion Operation........................................................................................................................................44 Reverse Operation.........................................................................................................................................45 Linked List Program in C ................................................................................................................................46 11. Doubly Linked List...................................................................................................................................55 Doubly Linked List Representation................................................................................................................55 Basic Operations............................................................................................................................................55 Insertion Operation .......................................................................................................................................56 Deletion Operation........................................................................................................................................57 Insertion at the End of an Operation.............................................................................................................57 Doubly Linked List Program in C....................................................................................................................58 12. Circular Linked List..................................................................................................................................67 Singly Linked List as Circular..........................................................................................................................67 Doubly Linked List as Circular........................................................................................................................67 Basic Operations............................................................................................................................................67 Insertion Operation .......................................................................................................................................68 Deletion Operation........................................................................................................................................68 Display List Operation....................................................................................................................................69 Circular Linked List Program in C...................................................................................................................69
- 6. Data Structures & Algorithms v STACK & QUEUE........................................................................................................................74 13. Stack.......................................................................................................................................................75 Stack Representation.....................................................................................................................................75 Basic Operations............................................................................................................................................76 peek().............................................................................................................................................................76 isfull().............................................................................................................................................................77 isempty()........................................................................................................................................................77 Push Operation..............................................................................................................................................78 Pop Operation ...............................................................................................................................................79 Stack Program in C.........................................................................................................................................81 14. Expression Parsing ..................................................................................................................................85 Infix Notation.................................................................................................................................................85 Prefix Notation ..............................................................................................................................................85 Postfix Notation.............................................................................................................................................85 Parsing Expressions .......................................................................................................................................86 Postfix Evaluation Algorithm .........................................................................................................................87 Expression Parsing Using Stack......................................................................................................................87 15. Queue.....................................................................................................................................................93 Queue Representation ..................................................................................................................................93 Basic Operations............................................................................................................................................93 peek().............................................................................................................................................................94 isfull().............................................................................................................................................................94 isempty()........................................................................................................................................................95 Enqueue Operation .......................................................................................................................................96 Dequeue Operation.......................................................................................................................................97 Queue Program in C ......................................................................................................................................99 SEARCHING TECHNIQUES........................................................................................................103 16. Linear Search ........................................................................................................................................104 Linear Search Program in C .........................................................................................................................105 17. Binary Search........................................................................................................................................108 How Binary Search Works? .........................................................................................................................108 Binary Search Program in C .........................................................................................................................111 18. Interpolation Search .............................................................................................................................115 Positioning in Binary Search ........................................................................................................................115 Position Probing in Interpolation Search.....................................................................................................116 Interpolation Search Program in C ..............................................................................................................118 19. Hash Table ............................................................................................................................................120 Hashing........................................................................................................................................................120 Linear Probing..............................................................................................................................................121 Basic Operations..........................................................................................................................................122 Data Item.....................................................................................................................................................122
- 7. Data Structures & Algorithms vi Hash Method...............................................................................................................................................122 Search Operation.........................................................................................................................................122 Insert Operation ..........................................................................................................................................123 Delete Operation.........................................................................................................................................124 Hash Table Program in C .............................................................................................................................125 SORTING TECHNIQUES............................................................................................................130 20. Sorting Algorithm..................................................................................................................................131 In-place Sorting and Not-in-place Sorting ...................................................................................................131 Stable and Not Stable Sorting......................................................................................................................131 Adaptive and Non-Adaptive Sorting Algorithm...........................................................................................132 Important Terms..........................................................................................................................................132 21. Bubble Sort Algorithm ..........................................................................................................................134 How Bubble Sort Works?.............................................................................................................................134 Bubble Sort Program in C ............................................................................................................................138 22. Insertion Sort........................................................................................................................................142 How Insertion Sort Works? .........................................................................................................................142 Insertion Sort Program in C .........................................................................................................................145 23. Selection Sort........................................................................................................................................149 How Selection Sort Works? .........................................................................................................................149 Selection Sort Program in C.........................................................................................................................152 24. Merge Sort Algorithm ...........................................................................................................................155 How Merge Sort Works? .............................................................................................................................155 Merge Sort Program in C.............................................................................................................................158 25. Shell Sort ..............................................................................................................................................160 How Shell Sort Works? ................................................................................................................................160 Shell Sort Program in C................................................................................................................................164 26. Quick Sort .............................................................................................................................................168 Partition in Quick Sort .................................................................................................................................168 Quick Sort Pivot Algorithm ..........................................................................................................................168 Quick Sort Pivot Pseudocode ......................................................................................................................169 Quick Sort Algorithm ...................................................................................................................................169 Quick Sort Pseudocode................................................................................................................................170 Quick Sort Program in C ..............................................................................................................................170 GRAPH DATA STRUCTURE.......................................................................................................174 27. Graphs ..................................................................................................................................................175 Graph Data Structure ..................................................................................................................................175 Basic Operations..........................................................................................................................................177
- 8. Data Structures & Algorithms vii 28. Depth First Traversal.............................................................................................................................178 Depth First Traversal in C ............................................................................................................................181 29. Breadth First Traversal..........................................................................................................................186 Breadth First Traversal in C .........................................................................................................................188 TREE DATA STRUCTURE ..........................................................................................................194 30. Tree ......................................................................................................................................................195 Important Terms..........................................................................................................................................195 Binary Search Tree Representation.............................................................................................................196 Tree Node....................................................................................................................................................196 BST Basic Operations...................................................................................................................................197 Insert Operation ..........................................................................................................................................197 Search Operation.........................................................................................................................................199 Tree Traversal in C.......................................................................................................................................200 31. Tree Traversal .......................................................................................................................................206 In-order Traversal........................................................................................................................................206 Pre-order Traversal......................................................................................................................................207 Post-order Traversal....................................................................................................................................208 Tree Traversal in C.......................................................................................................................................209 32. Binary Search Tree................................................................................................................................215 Representation............................................................................................................................................215 Basic Operations..........................................................................................................................................216 Node............................................................................................................................................................216 Search Operation.........................................................................................................................................216 Insert Operation ..........................................................................................................................................217 33. AVL Trees..............................................................................................................................................219 AVL Rotations ..............................................................................................................................................220 34. Spanning Tree.......................................................................................................................................224 General Properties of Spanning Tree ..........................................................................................................224 Mathematical Properties of Spanning Tree.................................................................................................225 Application of Spanning Tree ......................................................................................................................225 Minimum Spanning Tree (MST)...................................................................................................................225 Minimum Spanning-Tree Algorithm............................................................................................................225 Kruskal's Spanning Tree Algorithm..............................................................................................................226 Prim's Spanning Tree Algorithm..................................................................................................................229 35. Heaps....................................................................................................................................................233 Max Heap Construction Algorithm..............................................................................................................234 Max Heap Deletion Algorithm.....................................................................................................................235 RECURSION.............................................................................................................................236
- 9. Data Structures & Algorithms viii 36. Recursion ─ Basics.................................................................................................................................237 Properties ....................................................................................................................................................237 Implementation...........................................................................................................................................238 Analysis of Recursion...................................................................................................................................238 Time Complexity..........................................................................................................................................238 Space Complexity ........................................................................................................................................239 37. Tower of Hanoi .....................................................................................................................................240 Rules ............................................................................................................................................................240 Algorithm.....................................................................................................................................................244 Tower of Hanoi in C .....................................................................................................................................247 38. Fibonacci Series ....................................................................................................................................251 Fibonacci Iterative Algorithm ......................................................................................................................252 Fibonacci Interactive Program in C..............................................................................................................252 Fibonacci Recursive Algorithm ....................................................................................................................254 Fibonacci Recursive Program in C................................................................................................................254
- 10. Data Structures & Algorithms 1 Basics
- 11. Data Structures & Algorithms 2 Data Structure is a systematic way to organize data in order to use it efficiently. Following terms are the foundation terms of a data structure. Interface − Each data structure has an interface. Interface represents the set of operations that a data structure supports. An interface only provides the list of supported operations, type of parameters they can accept and return type of these operations. Implementation − Implementation provides the internal representation of a data structure. Implementation also provides the definition of the algorithms used in the operations of the data structure. CharacteristicsofaDataStructure Correctness − Data structure implementation should implement its interface correctly. Time Complexity − Running time or the execution time of operations of data structure must be as small as possible. Space Complexity − Memory usage of a data structure operation should be as little as possible. NeedforDataStructure As applications are getting complex and data rich, there are three common problems that applications face now-a-days. Data Search − Consider an inventory of 1 million(106 ) items of a store. If the application is to search an item, it has to search an item in 1 million(106 ) items every time slowing down the search. As data grows, search will become slower. Processor Speed − Processor speed although being very high, falls limited if the data grows to billion records. Multiple Requests − As thousands of users can search data simultaneously on a web server, even the fast server fails while searching the data. To solve the above-mentioned problems, data structures come to rescue. Data can be organized in a data structure in such a way that all items may not be required to be searched, and the required data can be searched almost instantly. 1. Overview
- 12. Data Structures & Algorithms 3 ExecutionTimeCases There are three cases which are usually used to compare various data structure's execution time in a relative manner. Worst Case − This is the scenario where a particular data structure operation takes maximum time it can take. If an operation's worst case time is ƒ(n) then this operation will not take more than ƒ(n) time, where ƒ(n) represents function of n. Average Case − This is the scenario depicting the average execution time of an operation of a data structure. If an operation takes ƒ(n) time in execution, then m operations will take mƒ(n) time. Best Case − This is the scenario depicting the least possible execution time of an operation of a data structure. If an operation takes ƒ(n) time in execution, then the actual operation may take time as the random number which would be maximum as ƒ(n). BasicTerminology Data − Data are values or set of values. Data Item − Data item refers to single unit of values. Group Items − Data items that are divided into sub items are called as Group Items. Elementary Items − Data items that cannot be divided are called as Elementary Items. Attribute and Entity − An entity is that which contains certain attributes or properties, which may be assigned values. Entity Set − Entities of similar attributes form an entity set. Field − Field is a single elementary unit of information representing an attribute of an entity. Record − Record is a collection of field values of a given entity. File − File is a collection of records of the entities in a given entity set.
- 13. Data Structures & Algorithms 4 TryitOptionOnline You really do not need to set up your own environment to start learning C programming language. Reason is very simple, we already have set up C Programming environment online, so that you can compile and execute all the available examples online at the same time when you are doing your theory work. This gives you confidence in what you are reading and to check the result with different options. Feel free to modify any example and execute it online. Try the following example using the Try it option available at the top right corner of the sample code box − #include <stdio.h> int main(){ /* My first program in C */ printf("Hello, World! n"); return 0; } For most of the examples given in this tutorial, you will find Try it option, so just make use of it and enjoy your learning. LocalEnvironmentSetup If you are still willing to set up your environment for C programming language, you need the following two tools available on your computer, (a) Text Editor and (b) The C Compiler. Text Editor This will be used to type your program. Examples of few editors include Windows Notepad, OS Edit command, Brief, Epsilon, EMACS, and vim or vi. The name and the version of the text editor can vary on different operating systems. For example, Notepad will be used on Windows, and vim or vi can be used on Windows as well as Linux or UNIX. The files you create with your editor are called source files and contain program source code. The source files for C programs are typically named with the extension ".c". Before starting your programming, make sure you have one text editor in place and you have enough experience to write a computer program, save it in a file, compile it, and finally execute it. 2. Environment Setup
- 14. Data Structures & Algorithms 5 The C Compiler The source code written in the source file is the human readable source for your program. It needs to be "compiled", to turn into machine language so that your CPU can actually execute the program as per the given instructions. This C programming language compiler will be used to compile your source code into a final executable program. We assume you have the basic knowledge about a programming language compiler. Most frequently used and free available compiler is GNU C/C++ compiler. Otherwise, you can have compilers either from HP or Solaris if you have respective Operating Systems (OS). The following section guides you on how to install GNU C/C++ compiler on various OS. We are mentioning C/C++ together because GNU GCC compiler works for both C and C++ programming languages. InstallationonUNIX/Linux If you are using Linux or UNIX, then check whether GCC is installed on your system by entering the following command from the command line − $ gcc -v If you have GNU compiler installed on your machine, then it should print a message such as the following − Using built-in specs. Target: i386-redhat-linux Configured with: ../configure --prefix=/usr ....... Thread model: posix gcc version 4.1.2 20080704 (Red Hat 4.1.2-46) If GCC is not installed, then you will have to install it yourself using the detailed instructions available at http://gcc.gnu.org/install/ This tutorial has been written based on Linux and all the given examples have been compiled on Cent OS flavor of Linux system. InstallationonMacOS If you use Mac OS X, the easiest way to obtain GCC is to download the Xcode development environment from Apple's website and follow the simple installation instructions. Once you have Xcode setup, you will be able to use GNU compiler for C/C++. Xcode is currently available at developer.apple.com/technologies/tools/
- 15. Data Structures & Algorithms 6 InstallationonWindows To install GCC on Windows, you need to install MinGW. To install MinGW, go to the MinGW homepage, www.mingw.org, and follow the link to the MinGW download page. Download the latest version of the MinGW installation program, which should be named MinGW- <version>.exe. While installing MinWG, at a minimum, you must install gcc-core, gcc-g++, binutils, and the MinGW runtime, but you may wish to install more. Add the bin subdirectory of your MinGW installation to your PATH environment variable, so that you can specify these tools on the command line by their simple names. When the installation is complete, you will be able to run gcc, g++, ar, ranlib, dlltool, and several other GNU tools from the Windows command line.
- 16. Data Structures & Algorithms 7 Algorithm
- 17. Data Structures & Algorithms 8 Algorithm is a step-by-step procedure, which defines a set of instructions to be executed in a certain order to get the desired output. Algorithms are generally created independent of underlying languages, i.e. an algorithm can be implemented in more than one programming language. From the data structure point of view, following are some important categories of algorithms − Search − Algorithm to search an item in a data structure. Sort − Algorithm to sort items in a certain order. Insert − Algorithm to insert item in a data structure. Update − Algorithm to update an existing item in a data structure. Delete − Algorithm to delete an existing item from a data structure. CharacteristicsofanAlgorithm Not all procedures can be called an algorithm. An algorithm should have the following characteristics − Unambiguous − Algorithm should be clear and unambiguous. Each of its steps (or phases), and their inputs/outputs should be clear and must lead to only one meaning. Input − An algorithm should have 0 or more well-defined inputs. Output − An algorithm should have 1 or more well-defined outputs, and should match the desired output. Finiteness − Algorithms must terminate after a finite number of steps. Feasibility − Should be feasible with the available resources. Independent − An algorithm should have step-by-step directions, which should be independent of any programming code. 3. Algorithms ─ Basics
- 18. Data Structures & Algorithms 9 HowtoWriteanAlgorithm? There are no well-defined standards for writing algorithms. Rather, it is problem and resource dependent. Algorithms are never written to support a particular programming code. As we know that all programming languages share basic code constructs like loops (do, for, while), flow-control (if-else), etc. These common constructs can be used to write an algorithm. We write algorithms in a step-by-step manner, but it is not always the case. Algorithm writing is a process and is executed after the problem domain is well-defined. That is, we should know the problem domain, for which we are designing a solution. Example Let's try to learn algorithm-writing by using an example. Problem − Design an algorithm to add two numbers and display the result. step 1 − START step 2 − declare three integers a, b & c step 3 − define values of a & b step 4 − add values of a & b step 5 − store output of step 4 to c step 6 − print c step 7 − STOP Algorithms tell the programmers how to code the program. Alternatively, the algorithm can be written as − step 1 − START ADD step 2 − get values of a & b step 3 − c ← a + b step 4 − display c step 5 − STOP In design and analysis of algorithms, usually the second method is used to describe an algorithm. It makes it easy for the analyst to analyze the algorithm ignoring all unwanted definitions. He can observe what operations are being used and how the process is flowing. Writing step numbers, is optional. We design an algorithm to get a solution of a given problem. A problem can be solved in more than one ways.
- 19. Data Structures & Algorithms 10 Hence, many solution algorithms can be derived for a given problem. The next step is to analyze those proposed solution algorithms and implement the best suitable solution. AlgorithmAnalysis Efficiency of an algorithm can be analyzed at two different stages, before implementation and after implementation. They are the following − A Priori Analysis − This is a theoretical analysis of an algorithm. Efficiency of an algorithm is measured by assuming that all other factors, for example, processor speed, are constant and have no effect on the implementation. A Posterior Analysis − This is an empirical analysis of an algorithm. The selected algorithm is implemented using programming language. This is then executed on target computer machine. In this analysis, actual statistics like running time and space required, are collected. We shall learn about a priori algorithm analysis. Algorithm analysis deals with the execution or running time of various operations involved. The running time of an operation can be defined as the number of computer instructions executed per operation.
- 20. Data Structures & Algorithms 11 AlgorithmComplexity Suppose X is an algorithm and n is the size of input data, the time and space used by the algorithm X are the two main factors, which decide the efficiency of X. Time Factor – Time is measured by counting the number of key operations such as comparisons in the sorting algorithm. Space Factor − Space is measured by counting the maximum memory space required by the algorithm. The complexity of an algorithm f(n) gives the running time and/or the storage space required by the algorithm in terms of n as the size of input data. SpaceComplexity Space complexity of an algorithm represents the amount of memory space required by the algorithm in its life cycle. The space required by an algorithm is equal to the sum of the following two components − A fixed part that is a space required to store certain data and variables, that are independent of the size of the problem. For example, simple variables and constants used, program size, etc. A variable part is a space required by variables, whose size depends on the size of the problem. For example, dynamic memory allocation, recursion stack space, etc. Space complexity S(P) of any algorithm P is S(P) = C + SP(I), where C is the fixed part and S(I) is the variable part of the algorithm, which depends on instance characteristic I. Following is a simple example that tries to explain the concept − Algorithm: SUM(A, B) Step 1 - START Step 2 - C ← A + B + 10 Step 3 - Stop Here we have three variables A, B, and C and one constant. Hence S(P) = 1+3. Now, space depends on data types of given variables and constant types and it will be multiplied accordingly. TimeComplexity Time complexity of an algorithm represents the amount of time required by the algorithm to run to completion. Time requirements can be defined as a numerical function T(n), where T(n) can be measured as the number of steps, provided each step consumes constant time. For example, addition of two n-bit integers takes n steps. Consequently, the total computational time is T(n) = c*n, where c is the time taken for the addition of two bits. Here, we observe that T(n) grows linearly as the input size increases.
- 21. Data Structures & Algorithms 12 Asymptotic analysis of an algorithm refers to defining the mathematical boundation/framing of its run-time performance. Using asymptotic analysis, we can very well conclude the best case, average case, and worst case scenario of an algorithm. Asymptotic analysis is input bound i.e., if there's no input to the algorithm, it is concluded to work in a constant time. Other than the "input" all other factors are considered constant. Asymptotic analysis refers to computing the running time of any operation in mathematical units of computation. For example, the running time of one operation is computed as f(n) and may be for another operation it is computed as g(n2 ). This means the first operation running time will increase linearly with the increase in n and the running time of the second operation will increase exponentially when n increases. Similarly, the running time of both operations will be nearly the same if n is significantly small. Usually, the time required by an algorithm falls under three types − Best Case − Minimum time required for program execution. Average Case − Average time required for program execution. Worst Case − Maximum time required for program execution. AsymptoticNotations Following are the commonly used asymptotic notations to calculate the running time complexity of an algorithm. Ο Notation Ω Notation θ Notation Big Oh Notation, Ο The notation Ο(n) is the formal way to express the upper bound of an algorithm's running time. It measures the worst case time complexity or the longest amount of time an algorithm can possibly take to complete. 4. Asymptotic Analysis
- 22. Data Structures & Algorithms 13 For example, for a function f(n) Ο(f(n)) = { g(n) : there exists c > 0 and n0 such that g(n) ≤ c.f(n) for all n > n0. } Omega Notation, Ω The notation Ω(n) is the formal way to express the lower bound of an algorithm's running time. It measures the best case time complexity or the best amount of time an algorithm can possibly take to complete.
- 23. Data Structures & Algorithms 14 For example, for a function f(n) Ω(f(n)) ≥ { g(n) : there exists c > 0 and n0 such that g(n) ≤ c.f(n) for all n > n0. } Theta Notation, θ The notation θ(n) is the formal way to express both the lower bound and the upper bound of an algorithm's running time. It is represented as follows − θ(f(n)) = { g(n) if and only if g(n) = Ο(f(n)) and g(n) = Ω(f(n)) for all n > n0. }
- 24. Data Structures & Algorithms 15 CommonAsymptoticNotations Following is a list of some common asymptotic notations: constant − Ο(1) logarithmic − Ο(log n) linear − Ο(n) n log n − Ο(n log n) quadratic − Ο(n2 ) cubic − Ο(n3 ) polynomial − nΟ(1) exponential − 2Ο(n)
- 25. Data Structures & Algorithms 16 An algorithm is designed to achieve optimum solution for a given problem. In greedy algorithm approach, decisions are made from the given solution domain. As being greedy, the closest solution that seems to provide an optimum solution is chosen. Greedy algorithms try to find a localized optimum solution, which may eventually lead to globally optimized solutions. However, generally greedy algorithms do not provide globally optimized solutions. CountingCoins This problem is to count to a desired value by choosing the least possible coins and the greedy approach forces the algorithm to pick the largest possible coin. If we are provided coins of € 1, 2, 5 and 10 and we are asked to count € 18 then the greedy procedure will be − 1 − Select one € 10 coin, the remaining count is 8 2 − Then select one € 5 coin, the remaining count is 3 3 − Then select one € 2 coin, the remaining count is 1 3 − And finally, the selection of one € 1 coins solves the problem Though, it seems to be working fine, for this count we need to pick only 4 coins. But if we slightly change the problem then the same approach may not be able to produce the same optimum result. For the currency system, where we have coins of 1, 7, 10 value, counting coins for value 18 will be absolutely optimum but for count like 15, it may use more coins than necessary. For example, the greedy approach will use 10 + 1 + 1 + 1 + 1 + 1, total 6 coins. Whereas the same problem could be solved by using only 3 coins (7 + 7 + 1) Hence, we may conclude that the greedy approach picks an immediate optimized solution and may fail where global optimization is a major concern. 5. Greedy Algorithms
- 26. Data Structures & Algorithms 17 Examples Most networking algorithms use the greedy approach. Here is a list of few of them − Travelling Salesman Problem Prim's Minimal Spanning Tree Algorithm Kruskal's Minimal Spanning Tree Algorithm Dijkstra's Minimal Spanning Tree Algorithm Graph - Map Coloring Graph - Vertex Cover Knapsack Problem Job Scheduling Problem There are lots of similar problems that uses the greedy approach to find an optimum solution.
- 27. Data Structures & Algorithms 18 In divide and conquer approach, the problem in hand, is divided into smaller sub-problems and then each problem is solved independently. When we keep on dividing the sub- problems into even smaller sub-problems, we may eventually reach a stage where no more division is possible. Those "atomic" smallest possible sub-problem (fractions) are solved. The solution of all sub-problems is finally merged in order to obtain the solution of an original problem. Broadly, we can understand divide-and-conquer approach in a three-step process. Divide/Break This step involves breaking the problem into smaller sub-problems. Sub-problems should represent a part of the original problem. This step generally takes a recursive approach to divide the problem until no sub-problem is further divisible. At this stage, sub-problems become atomic in nature but still represent some part of the actual problem. Conquer/Solve This step receives a lot of smaller sub-problems to be solved. Generally, at this level, the problems are considered 'solved' on their own. 6. Divide &Conquer
- 28. Data Structures & Algorithms 19 Merge/Combine When the smaller sub-problems are solved, this stage recursively combines them until they formulate a solution of the original problem. This algorithmic approach works recursively and conquer & merge steps works so close that they appear as one. Examples The following computer algorithms are based on divide-and-conquer programming approach − Merge Sort Quick Sort Binary Search Strassen's Matrix Multiplication Closest Pair (points) There are various ways available to solve any computer problem, but the mentioned are a good example of divide and conquer approach.
- 29. Data Structures & Algorithms 20 Dynamic programming approach is similar to divide and conquer in breaking down the problem into smaller and yet smaller possible sub-problems. But unlike, divide and conquer, these sub-problems are not solved independently. Rather, results of these smaller sub-problems are remembered and used for similar or overlapping sub-problems. Dynamic programming is used where we have problems, which can be divided into similar sub-problems, so that their results can be re-used. Mostly, these algorithms are used for optimization. Before solving the in-hand sub-problem, dynamic algorithm will try to examine the results of the previously solved sub-problems. The solutions of sub-problems are combined in order to achieve the best solution. So we can say − The problem should be able to be divided into smaller overlapping sub-problem. An optimum solution can be achieved by using an optimum solution of smaller sub- problems. Dynamic algorithms use memorization. Comparison In contrast to greedy algorithms, where local optimization is addressed, dynamic algorithms are motivated for an overall optimization of the problem. In contrast to divide and conquer algorithms, where solutions are combined to achieve an overall solution, dynamic algorithms use the output of a smaller sub-problem and then try to optimize a bigger sub-problem. Dynamic algorithms use memorization to remember the output of already solved sub-problems. Example The following computer problems can be solved using dynamic programming approach − Fibonacci number series Knapsack problem Tower of Hanoi All pair shortest path by Floyd-Warshall Shortest path by Dijkstra Project scheduling Dynamic programming can be used in both top-down and bottom-up manner. And of course, most of the times, referring to the previous solution output is cheaper than re- computing in terms of CPU cycles. 7. Dynamic Programming
- 30. Data Structures & Algorithms 21 Data Structures
- 31. Data Structures & Algorithms 22 This chapter explains the basic terms related to data structure. DataDefinition Data Definition defines a particular data with the following characteristics. Atomic − Definition should define a single concept. Traceable − Definition should be able to be mapped to some data element. Accurate − Definition should be unambiguous. Clear and Concise − Definition should be understandable. DataObject Data Object represents an object having a data. DataType Data type is a way to classify various types of data such as integer, string, etc. which determines the values that can be used with the corresponding type of data, the type of operations that can be performed on the corresponding type of data. There are two data types − Built-in Data Type Derived Data Type Built-in Data Type Those data types for which a language has built-in support are known as Built-in Data types. For example, most of the languages provide the following built-in data types. Integers Boolean (true, false) Floating (Decimal numbers) Character and Strings 8. Basic Concepts
- 32. Data Structures & Algorithms 23 Derived Data Type Those data types which are implementation independent as they can be implemented in one or the other way are known as derived data types. These data types are normally built by the combination of primary or built-in data types and associated operations on them. For example − List Array Stack Queue BasicOperations The data in the data structures are processed by certain operations. The particular data structure chosen largely depends on the frequency of the operation that needs to be performed on the data structure. Traversing Searching Insertion Deletion Sorting Merging
- 33. Data Structures & Algorithms 24 Array is a container which can hold a fix number of items and these items should be of the same type. Most of the data structures make use of arrays to implement their algorithms. Following are the important terms to understand the concept of Array. Element − Each item stored in an array is called an element. Index − Each location of an element in an array has a numerical index, which is used to identify the element. ArrayRepresentation Arrays can be declared in various ways in different languages. For illustration, let's take C array declaration. Arrays can be declared in various ways in different languages. For illustration, let's take C array declaration. As per the above illustration, following are the important points to be considered. Index starts with 0. Array length is 8 which means it can store 8 elements. Each element can be accessed via its index. For example, we can fetch an element at index 6 as 9. 9. Arrays
- 34. Data Structures & Algorithms 25 BasicOperations Following are the basic operations supported by an array. Traverse − Prints all the array elements one by one. Insertion − Adds an element at the given index. Deletion − Deletes an element at the given index. Search − Searches an element using the given index or by the value. Update − Updates an element at the given index. In C, when an array is initialized with size, then it assigns defaults values to its elements in following order. Data Type Default Value bool false char 0 int 0 float 0.0 double 0.0f void wchar_t 0 InsertionOperation Insert operation is to insert one or more data elements into an array. Based on the requirement, a new element can be added at the beginning, end, or any given index of array. Here, we see a practical implementation of insertion operation, where we add data at the end of the array − Algorithm Let Array be a linear unordered array of MAX elements.
- 35. Data Structures & Algorithms 26 Example Result Let LA be a Linear Array (unordered) with N elements and K is a positive integer such that K<=N. Following is the algorithm where ITEM is inserted into the Kth position of LA − 1. Start 2. Set J=N 3. Set N = N+1 4. Repeat steps 5 and 6 while J >= K 5. Set LA[J+1] = LA[J] 6. Set J = J-1 7. Set LA[K] = ITEM 8. Stop Example Following is the implementation of the above algorithm − #include <stdio.h> main() { int LA[] = {1,3,5,7,8}; int item = 10, k = 3, n = 5; int i = 0, j = n; printf("The original array elements are :n"); for(i = 0; i<n; i++) { printf("LA[%d] = %d n", i, LA[i]); } n = n + 1; while( j >= k){ LA[j+1] = LA[j]; j = j - 1; }
- 36. Data Structures & Algorithms 27 LA[k] = item; printf("The array elements after insertion :n"); for(i = 0; i<n; i++) { printf("LA[%d] = %d n", i, LA[i]); } } When we compile and execute the above program, it produces the following result − The original array elements are : LA[0]=1 LA[1]=3 LA[2]=5 LA[3]=7 LA[4]=8 The array elements after insertion : LA[0]=1 LA[1]=3 LA[2]=5 LA[3]=10 LA[4]=7 LA[5]=8 For other variations of array insertion operation click here ArrayInsertions In the previous section, we have learnt how the insertion operation works. It is not always necessary that an element is inserted at the end of an array. Following can be a situation with array insertion − Insertion at the beginning of an array Insertion at the given index of an array Insertion after the given index of an array Insertion before the given index of an array
- 37. Data Structures & Algorithms 28 InsertionattheBeginningofanArray When the insertion happens at the beginning, it causes all the existing data items to shift one step downward. Here, we design and implement an algorithm to insert an element at the beginning of an array. Algorithm We assume A is an array with N elements. The maximum numbers of elements it can store is defined by MAX. We shall first check if an array has any empty space to store any element and then we proceed with the insertion process. begin IF N = MAX, return ELSE N = N + 1 For All Elements in A Move to next adjacent location A[FIRST] = New_Element end Implementation in C #include <stdio.h> #define MAX 5 void main() { int array[MAX] = {2, 3, 4, 5}; int N = 4; // number of elements in array int i = 0; // loop variable int value = 1; // new data element to be stored in array // print array before insertion printf("Printing array before insertion −n");
- 38. Data Structures & Algorithms 29 for(i = 0; i < N; i++) { printf("array[%d] = %d n", i, array[i]); } // now shift rest of the elements downwards for(i = N; i >= 0; i--) { array[i+1] = array[i]; } // add new element at first position array[0] = value; // increase N to reflect number of elements N++; // print to confirm printf("Printing array after insertion −n"); for(i = 0; i < N; i++) { printf("array[%d] = %dn", i, array[i]); } } This program should yield the following output − Printing array before insertion − array[0] = 2 array[1] = 3 array[2] = 4 array[3] = 5 Printing array after insertion − array[0] = 0 array[1] = 2 array[2] = 3 array[3] = 4 array[4] = 5
- 39. Data Structures & Algorithms 30 InsertionattheGivenIndexofanArray In this scenario, we are given the exact location (index) of an array where a new data element (value) needs to be inserted. First we shall check if the array is full, if it is not, then we shall move all data elements from that location one step downward. This will make room for a new data element. Algorithm We assume A is an array with N elements. The maximum numbers of elements it can store is defined by MAX. begin IF N = MAX, return ELSE N = N + 1 SEEK Location index For All Elements from A[index] to A[N] Move to next adjacent location A[index] = New_Element end Implementation in C #include <stdio.h> #define MAX 5 void main() { int array[MAX] = {1, 2, 4, 5}; int N = 4; // number of elements in array int i = 0; // loop variable int index = 2; // index location to insert new value int value = 3; // new data element to be inserted // print array before insertion printf("Printing array before insertion −n");
- 40. Data Structures & Algorithms 31 for(i = 0; i < N; i++) { printf("array[%d] = %d n", i, array[i]); } // now shift rest of the elements downwards for(i = N; i >= index; i--) { array[i+1] = array[i]; } // add new element at first position array[index] = value; // increase N to reflect number of elements N++; // print to confirm printf("Printing array after insertion −n"); for(i = 0; i < N; i++) { printf("array[%d] = %dn", i, array[i]); } } If we compile and run the above program, it will produce the following result − Printing array before insertion − array[0] = 1 array[1] = 2 array[2] = 4 array[3] = 5 Printing array after insertion − array[0] = 1 array[1] = 2 array[2] = 3 array[3] = 4 array[4] = 5
- 41. Data Structures & Algorithms 32 InsertionAftertheGivenIndexofanArray In this scenario we are given a location (index) of an array after which a new data element (value) has to be inserted. Only the seek process varies, the rest of the activities are the same as in the previous example. Algorithm We assume A is an array with N elements. The maximum numbers of elements it can store is defined by MAX. begin IF N = MAX, return ELSE N = N + 1 SEEK Location index For All Elements from A[index + 1] to A[N] Move to next adjacent location A[index + 1] = New_Element end Implementation in C #include <stdio.h> #define MAX 5 void main() { int array[MAX] = {1, 2, 4, 5}; int N = 4; // number of elements in array int i = 0; // loop variable int index = 1; // index location after which value will be inserted int value = 3; // new data element to be inserted // print array before insertion printf("Printing array before insertion −n");
- 42. Data Structures & Algorithms 33 for(i = 0; i < N; i++) { printf("array[%d] = %d n", i, array[i]); } // now shift rest of the elements downwards for(i = N; i >= index + 1; i--) { array[i + 1] = array[i]; } // add new element at first position array[index + 1] = value; // increase N to reflect number of elements N++; // print to confirm printf("Printing array after insertion −n"); for(i = 0; i < N; i++) { printf("array[%d] = %dn", i, array[i]); } } If we compile and run the above program, it will produce the following result − Printing array before insertion − array[0] = 1 array[1] = 2 array[2] = 4 array[3] = 5 Printing array after insertion − array[0] = 1 array[1] = 2 array[2] = 3 array[3] = 4
- 43. Data Structures & Algorithms 34 array[4] = 5 InsertionBeforetheGivenIndexofanArray In this scenario we are given a location (index) of an array before which a new data element (value) has to be inserted. This time we seek till index-1, i.e., one location ahead of the given index. Rest of the activities are the same as in the previous example. Algorithm We assume A is an array with N elements. The maximum numbers of elements it can store is defined by MAX. begin IF N = MAX, return ELSE N = N + 1 SEEK Location index For All Elements from A[index - 1] to A[N] Move to next adjacent location A[index - 1] = New_Element end Implementation in C #include <stdio.h> #define MAX 5
- 44. Data Structures & Algorithms 35 void main() { int array[MAX] = {1, 2, 4, 5}; int N = 4; // number of elements in array int i = 0; // loop variable int index = 3; // index location before which value will be inserted int value = 3; // new data element to be inserted // print array before insertion printf("Printing array before insertion −n"); for(i = 0; i < N; i++) { printf("array[%d] = %d n", i, array[i]); } // now shift rest of the elements downwards for(i = N; i >= index + 1; i--) { array[i + 1] = array[i]; } // add new element at first position array[index + 1] = value; // increase N to reflect number of elements N++; // print to confirm printf("Printing array after insertion −n"); for(i = 0; i < N; i++) { printf("array[%d] = %dn", i, array[i]); } } If we compile and run the above program, it will produce the following result − Printing array before insertion − array[0] = 1 array[1] = 2
- 45. Data Structures & Algorithms 36 array[2] = 4 array[3] = 5 Printing array after insertion − array[0] = 1 array[1] = 2 array[2] = 4 array[3] = 5 array[4] = 3 DeletionOperation Deletion refers to removing an existing element from the array and re-organizing all elements of an array. Algorithm Consider LA is a linear array with N elements and K is a positive integer such that K<=N. Following is the algorithm to delete an element available at the Kth position of LA. 1. Start 2. Set J=K 3. Repeat steps 4 and 5 while J < N 4. Set LA[J-1] = LA[J] 5. Set J = J+1 6. Set N = N-1 7. Stop Example Following is the implementation of the above algorithm − #include <stdio.h> main() { int LA[] = {1,3,5,7,8}; int k = 3, n = 5; int i, j; printf("The original array elements are :n");
- 46. Data Structures & Algorithms 37 for(i = 0; i<n; i++) { printf("LA[%d] = %d n", i, LA[i]); } j = k; while( j < n){ LA[j-1] = LA[j]; j = j + 1; } n = n -1; printf("The array elements after deletion :n"); for(i = 0; i<n; i++) { printf("LA[%d] = %d n", i, LA[i]); } } When we compile and execute the above program, it produces the following result − The original array elements are : LA[0]=1 LA[1]=3 LA[2]=5 LA[3]=7 LA[4]=8 The array elements after deletion : LA[0]=1 LA[1]=3 LA[2]=7 LA[3]=8 SearchOperation You can perform a search for an array element based on its value or its index. Algorithm
- 47. Data Structures & Algorithms 38 Consider LA is a linear array with N elements and K is a positive integer such that K<=N. Following is the algorithm to find an element with a value of ITEM using sequential search. 1. Start 2. Set J=0 3. Repeat steps 4 and 5 while J < N 4. IF LA[J] is equal ITEM THEN GOTO STEP 6 5. Set J = J +1 6. PRINT J, ITEM 7. Stop Example Following is the implementation of the above algorithm − #include <stdio.h> main() { int LA[] = {1,3,5,7,8}; int item = 5, n = 5; int i = 0, j = 0; printf("The original array elements are :n"); for(i = 0; i<n; i++) { printf("LA[%d] = %d n", i, LA[i]); } while( j < n){ if( LA[j] == item ){ break; } j = j + 1; } printf("Found element %d at position %dn", item, j+1); } When we compile and execute the above program, it produces the following result −
- 48. Data Structures & Algorithms 39 The original array elements are : LA[0]=1 LA[1]=3 LA[2]=5 LA[3]=7 LA[4]=8 Found element 5 at position 3 UpdateOperation Update operation refers to updating an existing element from the array at a given index. Algorithm Consider LA is a linear array with N elements and K is a positive integer such that K<=N. Following is the algorithm to update an element available at the Kth position of LA. 1. Start 2. Set LA[K-1] = ITEM 3. Stop Example Following is the implementation of the above algorithm − #include <stdio.h> main() { int LA[] = {1,3,5,7,8}; int k = 3, n = 5, item = 10; int i, j; printf("The original array elements are :n"); for(i = 0; i<n; i++) { printf("LA[%d] = %d n", i, LA[i]); } LA[k-1] = item; printf("The array elements after updation :n");
- 49. Data Structures & Algorithms 40 for(i = 0; i<n; i++) { printf("LA[%d] = %d n", i, LA[i]); } } When we compile and execute the above program, it produces the following result − The original array elements are : LA[0]=1 LA[1]=3 LA[2]=5 LA[3]=7 LA[4]=8 The array elements after updation : LA[0]=1 LA[1]=3 LA[2]=10 LA[3]=7 LA[4]=8
- 50. Data Structures & Algorithms 41 Linked List
- 51. Data Structures & Algorithms 42 A linked list is a sequence of data structures, which are connected together via links. Linked List is a sequence of links which contains items. Each link contains a connection to another link. Linked list is the second most-used data structure after array. Following are the important terms to understand the concept of Linked List. Link − Each link of a linked list can store a data called an element. Next − Each link of a linked list contains a link to the next link called Next. Linked List − A Linked List contains the connection link to the first link called First. LinkedListRepresentation Linked list can be visualized as a chain of nodes, where every node points to the next node. As per the above illustration, following are the important points to be considered. Linked List contains a link element called first. Each link carries a data field(s) and a link field called next. Each link is linked with its next link using its next link. Last link carries a link as null to mark the end of the list. TypesofLinkedList Following are the various types of linked list. Simple Linked List − Item navigation is forward only. Doubly Linked List − Items can be navigated forward and backward. Circular Linked List − Last item contains link of the first element as next and the first element has a link to the last element as previous. 10. Linked List ─ Basics
- 52. Data Structures & Algorithms 43 BasicOperations Following are the basic operations supported by a list. Insertion − Adds an element at the beginning of the list. Deletion − Deletes an element at the beginning of the list. Display − Displays the complete list. Search − Searches an element using the given key. Delete − Deletes an element using the given key. InsertionOperation Adding a new node in linked list is a more than one step activity. We shall learn this with diagrams here. First, create a node using the same structure and find the location where it has to be inserted. Imagine that we are inserting a node B (NewNode), between A (LeftNode) and C (RightNode). Then point B.next to C - NewNode.next −> RightNode; It should look like this −
- 53. Data Structures & Algorithms 44 Now, the next node at the left should point to the new node. LeftNode.next −> NewNode; This will put the new node in the middle of the two. The new list should look like this − Similar steps should be taken if the node is being inserted at the beginning of the list. While inserting it at the end, the second last node of the list should point to the new node and the new node will point to NULL. DeletionOperation Deletion is also a more than one step process. We shall learn with pictorial representation. First, locate the target node to be removed, by using searching algorithms. The left (previous) node of the target node now should point to the next node of the target node − LeftNode.next −> TargetNode.next;
- 54. Data Structures & Algorithms 45 This will remove the link that was pointing to the target node. Now, using the following code, we will remove what the target node is pointing at. TargetNode.next −> NULL; We need to use the deleted node. We can keep that in memory otherwise we can simply deallocate memory and wipe off the target node completely. ReverseOperation This operation is a thorough one. We need to make the last node to be pointed by the head node and reverse the whole linked list. First, we traverse to the end of the list. It should be pointing to NULL. Now, we shall make it point to its previous node −
- 55. Data Structures & Algorithms 46 We have to make sure that the last node is not the lost node. So we'll have some temp node, which looks like the head node pointing to the last node. Now, we shall make all left side nodes point to their previous nodes one by one. Except the node (first node) pointed by the head node, all nodes should point to their predecessor, making them their new successor. The first node will point to NULL. We'll make the head node point to the new first node by using the temp node. The linked list is now reversed. To see linked list implementation in C programming language, please click here. LinkedListPrograminC A linked list is a sequence of data structures, which are connected together via links. Linked List is a sequence of links which contains items. Each link contains a connection to another link. Linked list is the second most-used data structure after array.
- 56. Data Structures & Algorithms 47 Implementation in C #include <stdio.h> #include <string.h> #include <stdlib.h> #include <stdbool.h> struct node { int data; int key; struct node *next; }; struct node *head = NULL; struct node *current = NULL; //display the list void printList() { struct node *ptr = head; printf("n[ "); //start from the beginning while(ptr != NULL) { printf("(%d,%d) ",ptr->key,ptr->data); ptr = ptr->next; } printf(" ]"); } //insert link at the first location void insertFirst(int key, int data) { //create a link
- 57. Data Structures & Algorithms 48 struct node *link = (struct node*) malloc(sizeof(struct node)); link->key = key; link->data = data; //point it to old first node link->next = head; //point first to new first node head = link; } //delete first item struct node* deleteFirst() { //save reference to first link struct node *tempLink = head; //mark next to first link as first head = head->next; //return the deleted link return tempLink; } //is list empty bool isEmpty() { return head == NULL; } int length() { int length = 0; struct node *current;
- 58. Data Structures & Algorithms 49 for(current = head; current != NULL; current = current->next) { length++; } return length; } //find a link with given key struct node* find(int key){ //start from the first link struct node* current = head; //if list is empty if(head == NULL) { return NULL; } //navigate through list while(current->key != key){ //if it is last node if(current->next == NULL){ return NULL; }else { //go to next link current = current->next; } } //if data found, return the current Link return current; }
- 59. Data Structures & Algorithms 50 //delete a link with given key struct node* delete(int key){ //start from the first link struct node* current = head; struct node* previous = NULL; //if list is empty if(head == NULL){ return NULL; } //navigate through list while(current->key != key){ //if it is last node if(current->next == NULL){ return NULL; }else { //store reference to current link previous = current; //move to next link current = current->next; } } //found a match, update the link if(current == head) { //change first to point to next link head = head->next; }else { //bypass the current link previous->next = current->next; } return current; }
- 60. Data Structures & Algorithms 51 void sort(){ int i, j, k, tempKey, tempData ; struct node *current; struct node *next; int size = length(); k = size ; for ( i = 0 ; i < size - 1 ; i++, k-- ) { current = head ; next = head->next ; for ( j = 1 ; j < k ; j++ ) { if ( current->data > next->data ) { tempData = current->data ; current->data = next->data; next->data = tempData ; tempKey = current->key; current->key = next->key; next->key = tempKey; } current = current->next; next = next->next; } } } void reverse(struct node** head_ref) { struct node* prev = NULL; struct node* current = *head_ref; struct node* next;
- 61. Data Structures & Algorithms 52 while (current != NULL) { next = current->next; current->next = prev; prev = current; current = next; } *head_ref = prev; } main() { insertFirst(1,10); insertFirst(2,20); insertFirst(3,30); insertFirst(4,1); insertFirst(5,40); insertFirst(6,56); printf("Original List: "); //print list printList(); while(!isEmpty()){ struct node *temp = deleteFirst(); printf("nDeleted value:"); printf("(%d,%d) ",temp->key,temp->data); } printf("nList after deleting all items: "); printList(); insertFirst(1,10); insertFirst(2,20); insertFirst(3,30); insertFirst(4,1);
- 62. Data Structures & Algorithms 53 insertFirst(5,40); insertFirst(6,56); printf("nRestored List: "); printList(); printf("n"); struct node *foundLink = find(4); if(foundLink != NULL){ printf("Element found: "); printf("(%d,%d) ",foundLink->key,foundLink->data); printf("n"); }else { printf("Element not found."); } delete(4); printf("List after deleting an item: "); printList(); printf("n"); foundLink = find(4); if(foundLink != NULL){ printf("Element found: "); printf("(%d,%d) ",foundLink->key,foundLink->data); printf("n"); }else { printf("Element not found."); } printf("n"); sort(); printf("List after sorting the data: "); printList(); reverse(&head);
- 63. Data Structures & Algorithms 54 printf("nList after reversing the data: "); printList(); } If we compile and run the above program, it will produce the following result − Original List: [ (6,56) (5,40) (4,1) (3,30) (2,20) (1,10) ] Deleted value:(6,56) Deleted value:(5,40) Deleted value:(4,1) Deleted value:(3,30) Deleted value:(2,20) Deleted value:(1,10) List after deleting all items: [ ] Restored List: [ (6,56) (5,40) (4,1) (3,30) (2,20) (1,10) ] Element found: (4,1) List after deleting an item: [ (6,56) (5,40) (3,30) (2,20) (1,10) ] Element not found. List after sorting the data: [ (1,10) (2,20) (3,30) (5,40) (6,56) ] List after reversing the data: [ (6,56) (5,40) (3,30) (2,20) (1,10) ]
- 64. Data Structures & Algorithms 55 Doubly Linked List is a variation of Linked list in which navigation is possible in both ways, either forward and backward easily as compared to Single Linked List. Following are the important terms to understand the concept of doubly linked list. Link − Each link of a linked list can store a data called an element. Next − Each link of a linked list contains a link to the next link called Next. Prev − Each link of a linked list contains a link to the previous link called Prev. Linked List − A Linked List contains the connection link to the first link called First and to the last link called Last. DoublyLinkedListRepresentation As per the above illustration, following are the important points to be considered. Doubly Linked List contains a link element called first and last. Each link carries a data field(s) and a link field called next. Each link is linked with its next link using its next link. Each link is linked with its previous link using its previous link. The last link carries a link as null to mark the end of the list. BasicOperations Following are the basic operations supported by a list. Insertion − Adds an element at the beginning of the list. Deletion − Deletes an element at the beginning of the list. Insert Last − Adds an element at the end of the list. Delete Last − Deletes an element from the end of the list. 11. Doubly Linked List
- 65. Data Structures & Algorithms 56 Insert After − Adds an element after an item of the list. Delete − Deletes an element from the list using the key. Display forward − Displays the complete list in a forward manner. Display backward − Displays the complete list in a backward manner. InsertionOperation Following code demonstrates the insertion operation at the beginning of a doubly linked list. //insert link at the first location void insertFirst(int key, int data) { //create a link struct node *link = (struct node*) malloc(sizeof(struct node)); link->key = key; link->data = data; if(isEmpty()) { //make it the last link last = link; }else { //update first prev link head->prev = link; } //point it to old first link link->next = head; //point first to new first link head = link; }
- 66. Data Structures & Algorithms 57 DeletionOperation Following code demonstrates the deletion operation at the beginning of a doubly linked list. //delete first item struct node* deleteFirst() { //save reference to first link struct node *tempLink = head; //if only one link if(head->next == NULL) { last = NULL; }else { head->next->prev = NULL; } head = head->next; //return the deleted link return tempLink; } InsertionattheEndofanOperation Following code demonstrates the insertion operation at the last position of a doubly linked list. //insert link at the last location void insertLast(int key, int data) { //create a link struct node *link = (struct node*) malloc(sizeof(struct node)); link->key = key; link->data = data;
- 67. Data Structures & Algorithms 58 if(isEmpty()) { //make it the last link last = link; }else { //make link a new last link last->next = link; //mark old last node as prev of new link link->prev = last; } //point last to new last node last = link; } To see the implementation in C programming language, please click here. DoublyLinkedListPrograminC Doubly Linked List is a variation of Linked list in which navigation is possible in both ways, either forward and backward easily as compared to Single Linked List. Implementation in C #include <stdio.h> #include <string.h> #include <stdlib.h> #include <stdbool.h> struct node { int data; int key; struct node *next; struct node *prev; };
- 68. Data Structures & Algorithms 59 //this link always point to first Link struct node *head = NULL; //this link always point to last Link struct node *last = NULL; struct node *current = NULL; //is list empty bool isEmpty(){ return head == NULL; } int length(){ int length = 0; struct node *current; for(current = head; current != NULL; current = current->next){ length++; } return length; } //display the list in from first to last void displayForward(){ //start from the beginning struct node *ptr = head; //navigate till the end of the list printf("n[ "); while(ptr != NULL){ printf("(%d,%d) ",ptr->key,ptr->data); ptr = ptr->next; }
- 69. Data Structures & Algorithms 60 printf(" ]"); } //display the list from last to first void displayBackward(){ //start from the last struct node *ptr = last; //navigate till the start of the list printf("n[ "); while(ptr != NULL){ //print data printf("(%d,%d) ",ptr->key,ptr->data); //move to next item ptr = ptr ->prev; printf(" "); } printf(" ]"); } //insert link at the first location void insertFirst(int key, int data){ //create a link struct node *link = (struct node*) malloc(sizeof(struct node)); link->key = key; link->data = data; if(isEmpty()){ //make it the last link last = link;
- 70. Data Structures & Algorithms 61 }else { //update first prev link head->prev = link; } //point it to old first link link->next = head; //point first to new first link head = link; } //insert link at the last location void insertLast(int key, int data){ //create a link struct node *link = (struct node*) malloc(sizeof(struct node)); link->key = key; link->data = data; if(isEmpty()){ //make it the last link last = link; }else { //make link a new last link last->next = link; //mark old last node as prev of new link link->prev = last; } //point last to new last node last = link; }
- 71. Data Structures & Algorithms 62 //delete first item struct node* deleteFirst(){ //save reference to first link struct node *tempLink = head; //if only one link if(head->next == NULL){ last = NULL; }else { head->next->prev = NULL; } head = head->next; //return the deleted link return tempLink; } //delete link at the last location struct node* deleteLast(){ //save reference to last link struct node *tempLink = last; //if only one link if(head->next == NULL){ head = NULL; }else { last->prev->next = NULL; } last = last->prev; //return the deleted link return tempLink; }
- 72. Data Structures & Algorithms 63 //delete a link with given key struct node* delete(int key){ //start from the first link struct node* current = head; struct node* previous = NULL; //if list is empty if(head == NULL){ return NULL; } //navigate through list while(current->key != key){ //if it is last node if(current->next == NULL){ return NULL; }else { //store reference to current link previous = current; //move to next link current = current->next; } } //found a match, update the link if(current == head) { //change first to point to next link head = head->next; }else { //bypass the current link
- 73. Data Structures & Algorithms 64 current->prev->next = current->next; } if(current == last){ //change last to point to prev link last = current->prev; }else { current->next->prev = current->prev; } return current; } bool insertAfter(int key, int newKey, int data){ //start from the first link struct node *current = head; //if list is empty if(head == NULL){ return false; } //navigate through list while(current->key != key){ //if it is last node if(current->next == NULL){ return false; }else { //move to next link current = current->next; } } //create a link struct node *newLink = (struct node*) malloc(sizeof(struct node)); newLink->key = key;
- 74. Data Structures & Algorithms 65 newLink->data = data; if(current == last) { newLink->next = NULL; last = newLink; }else { newLink->next = current->next; current->next->prev = newLink; } newLink->prev = current; current->next = newLink; return true; } main() { insertFirst(1,10); insertFirst(2,20); insertFirst(3,30); insertFirst(4,1); insertFirst(5,40); insertFirst(6,56); printf("nList (First to Last): "); displayForward(); printf("n"); printf("nList (Last to first): "); displayBackward(); printf("nList , after deleting first record: "); deleteFirst(); displayForward(); printf("nList , after deleting last record: ");
- 75. Data Structures & Algorithms 66 deleteLast(); displayForward(); printf("nList , insert after key(4) : "); insertAfter(4,7, 13); displayForward(); printf("nList , after delete key(4) : "); delete(4); displayForward(); } If we compile and run the above program, it will produce the following result − List (First to Last): [ (6,56) (5,40) (4,1) (3,30) (2,20) (1,10) ] List (Last to first): [ (1,10) (2,20) (3,30) (4,1) (5,40) (6,56) ] List , after deleting first record: [ (5,40) (4,1) (3,30) (2,20) (1,10) ] List , after deleting last record: [ (5,40) (4,1) (3,30) (2,20) ] List , insert after key(4) : [ (5,40) (4,1) (4,13) (3,30) (2,20) ] List , after delete key(4) : [ (5,40) (4,13) (3,30) (2,20) ]
- 76. Data Structures & Algorithms 67 Circular Linked List is a variation of Linked list in which the first element points to the last element and the last element points to the first element. Both Singly Linked List and Doubly Linked List can be made into a circular linked list. SinglyLinkedListasCircular In singly linked list, the next pointer of the last node points to the first node. DoublyLinkedListasCircular In doubly linked list, the next pointer of the last node points to the first node and the previous pointer of the first node points to the last node making the circular in both directions. As per the above illustration, following are the important points to be considered. The last link's next points to the first link of the list in both cases of singly as well as doubly linked list. The first link's previous points to the last of the list in case of doubly linked list. BasicOperations Following are the important operations supported by a circular list. insert − Inserts an element at the start of the list. delete – Deletes an element from the start of the list. display − Displays the list. 12. Circular Linked List
- 77. Data Structures & Algorithms 68 InsertionOperation Following code demonstrates the insertion operation in a circular linked list based on single linked list. //insert link at the first location void insertFirst(int key, int data) { //create a link struct node *link = (struct node*) malloc(sizeof(struct node)); link->key = key; link->data= data; if (isEmpty()) { head = link; head->next = head; }else { //point it to old first node link->next = head; //point first to new first node head = link; } } DeletionOperation Following code demonstrates the deletion operation in a circular linked list based on single linked list. //delete first item struct node * deleteFirst() { //save reference to first link struct node *tempLink = head; if(head->next == head){ head = NULL; return tempLink; }
- 78. Data Structures & Algorithms 69 //mark next to first link as first head = head->next; //return the deleted link return tempLink; } DisplayListOperation Following code demonstrates the display list operation in a circular linked list. //display the list void printList() { struct node *ptr = head; printf("n[ "); //start from the beginning if(head != NULL) { while(ptr->next != ptr) { printf("(%d,%d) ",ptr->key,ptr->data); ptr = ptr->next; } } printf(" ]"); } To know about its implementation in C programming language, please click here. CircularLinkedListPrograminC Circular Linked List is a variation of Linked list in which the first element points to the last element and the last element points to the first element. Both Singly Linked List and Doubly Linked List can be made into a circular linked list.
- 79. Data Structures & Algorithms 70 Implementation in C #include <stdio.h> #include <string.h> #include <stdlib.h> #include <stdbool.h> struct node { int data; int key; struct node *next; }; struct node *head = NULL; struct node *current = NULL; bool isEmpty(){ return head == NULL; } int length(){ int length = 0; //if list is empty if(head == NULL){ return 0; } current = head->next; while(current != head){ length++; current = current->next; }
- 80. Data Structures & Algorithms 71 return length; } //insert link at the first location void insertFirst(int key, int data){ //create a link struct node *link = (struct node*) malloc(sizeof(struct node)); link->key = key; link->data = data; if (isEmpty()) { head = link; head->next = head; }else { //point it to old first node link->next = head; //point first to new first node head = link; } } //delete first item struct node * deleteFirst(){ //save reference to first link struct node *tempLink = head; if(head->next == head){ head = NULL; return tempLink; }
- 81. Data Structures & Algorithms 72 //mark next to first link as first head = head->next; //return the deleted link return tempLink; } //display the list void printList(){ struct node *ptr = head; printf("n[ "); //start from the beginning if(head != NULL){ while(ptr->next != ptr){ printf("(%d,%d) ",ptr->key,ptr->data); ptr = ptr->next; } } printf(" ]"); } main() { insertFirst(1,10); insertFirst(2,20); insertFirst(3,30); insertFirst(4,1); insertFirst(5,40); insertFirst(6,56);
- 82. Data Structures & Algorithms 73 printf("Original List: "); //print list printList(); while(!isEmpty()){ struct node *temp = deleteFirst(); printf("nDeleted value:"); printf("(%d,%d) ",temp->key,temp->data); } printf("nList after deleting all items: "); printList(); } If we compile and run the above program, it will produce the following result − Original List: [ (6,56) (5,40) (4,1) (3,30) (2,20) ] Deleted value:(6,56) Deleted value:(5,40) Deleted value:(4,1) Deleted value:(3,30) Deleted value:(2,20) Deleted value:(1,10) List after deleting all items: [ ]
- 83. Data Structures & Algorithms 74 Stack & Queue
- 84. Data Structures & Algorithms 75 A stack is an Abstract Data Type (ADT), commonly used in most programming languages. It is named stack as it behaves like a real-world stack, for example – a deck of cards or a pile of plates, etc. A real-world stack allows operations at one end only. For example, we can place or remove a card or plate from the top of the stack only. Likewise, Stack ADT allows all data operations at one end only. At any given time, we can only access the top element of a stack. This feature makes it LIFO data structure. LIFO stands for Last-in-first-out. Here, the element which is placed (inserted or added) last, is accessed first. In stack terminology, insertion operation is called PUSH operation and removal operation is called POP operation. StackRepresentation The following diagram depicts a stack and its operations − A stack can be implemented by means of Array, Structure, Pointer, and Linked List. Stack can either be a fixed size one or it may have a sense of dynamic resizing. Here, we are going to implement stack using arrays, which makes it a fixed size stack implementation. 13. Stack
- 85. Data Structures & Algorithms 76 BasicOperations Stack operations may involve initializing the stack, using it and then de-initializing it. Apart from these basic stuffs, a stack is used for the following two primary operations − push() − Pushing (storing) an element on the stack. pop() − Removing (accessing) an element from the stack. When data is PUSHed onto stack. To use a stack efficiently, we need to check the status of stack as well. For the same purpose, the following functionality is added to stacks − peek() − get the top data element of the stack, without removing it. isFull() − check if stack is full. isEmpty() − check if stack is empty. At all times, we maintain a pointer to the last PUSHed data on the stack. As this pointer always represents the top of the stack, hence named top. The top pointer provides top value of the stack without actually removing it. First we should learn about procedures to support stack functions − peek() Algorithm of peek() function − begin procedure peek return stack[top] end procedure Implementation of peek() function in C programming language − int peek() { return stack[top]; }
- 86. Data Structures & Algorithms 77 isfull() Algorithm of isfull() function − begin procedure isfull if top equals to MAXSIZE return true else return false endif end procedure Implementation of isfull() function in C programming language − bool isfull() { if(top == MAXSIZE) return true; else return false; } isempty() Algorithm of isempty() function − begin procedure isempty if top less than 1 return true else return false endif end procedure
- 87. Data Structures & Algorithms 78 Implementation of isempty() function in C programming language is slightly different. We initialize top at -1, as the index in array starts from 0. So we check if the top is below zero or -1 to determine if the stack is empty. Here's the code − bool isempty() { if(top == -1) return true; else return false; } PushOperation The process of putting a new data element onto stack is known as a Push Operation. Push operation involves a series of steps − Step 1 − Checks if the stack is full. Step 2 − If the stack is full, produces an error and exit. Step 3 − If the stack is not full, increments top to point next empty space. Step 4 − Adds data element to the stack location, where top is pointing. Step 5 − Returns success.
- 88. Data Structures & Algorithms 79 If the linked list is used to implement the stack, then in step 3, we need to allocate space dynamically. Algorithm for PUSH Operation A simple algorithm for Push operation can be derived as follows − begin procedure push: stack, data if stack is full return null endif top ← top + 1 stack[top] ← data end procedure Implementation of this algorithm in C, is very easy. See the following code − void push(int data) { if(!isFull()) { top = top + 1; stack[top] = data; }else { printf("Could not insert data, Stack is full.n"); } } PopOperation Accessing the content while removing it from the stack, is known as a Pop Operation. In an array implementation of pop() operation, the data element is not actually removed, instead top is decremented to a lower position in the stack to point to the next value. But in linked-list implementation, pop() actually removes data element and deallocates memory space. A Pop operation may involve the following steps − Step 1 − Checks if the stack is empty. Step 2 − If the stack is empty, produces an error and exit.
- 89. Data Structures & Algorithms 80 Step 3 − If the stack is not empty, accesses the data element at which top is pointing. Step 4 − Decreases the value of top by 1. Step 5 − Returns success. Algorithm for Pop Operation A simple algorithm for Pop operation can be derived as follows − begin procedure pop: stack if stack is empty return null endif data ← stack[top] top ← top - 1 return data end procedure
- 90. Data Structures & Algorithms 81 Implementation of this algorithm in C, is as follows − int pop(int data) { if(!isempty()) { data = stack[top]; top = top - 1; return data; }else { printf("Could not retrieve data, Stack is empty.n"); } } For a complete stack program in C programming language, please click here. StackPrograminC We shall see the stack implementation in C programming language here. You can try the program by clicking on the Try-it button. To learn the theory aspect of stacks, click on visit previous page. Implementation in C #include <stdio.h> int MAXSIZE = 8; int stack[8]; int top = -1; int isempty() { if(top == -1) return 1; else return 0; }
- 91. Data Structures & Algorithms 82 int isfull() { if(top == MAXSIZE) return 1; else return 0; } int peek() { return stack[top]; } int pop() { int data; if(!isempty()) { data = stack[top]; top = top - 1; return data; }else { printf("Could not retrieve data, Stack is empty.n"); } } int push(int data) { if(!isfull()) { top = top + 1; stack[top] = data; }else { printf("Could not insert data, Stack is full.n"); } }
- 92. Data Structures & Algorithms 83 int main() { // push items on to the stack push(3); push(5); push(9); push(1); push(12); push(15); printf("Element at top of the stack: %dn" ,peek()); printf("Elements: n"); // print stack data while(!isempty()) { int data = pop(); printf("%dn",data); } printf("Stack full: %sn" , isfull()?"true":"false"); printf("Stack empty: %sn" , isempty()?"true":"false"); return 0; } If we compile and run the above program, it will produce the following result − Element at top of the stack: 15 Elements: 15 12 1 9 5 3 Stack full: false
- 93. Data Structures & Algorithms 84 Stack empty: true
- 94. Data Structures & Algorithms 85 The way to write arithmetic expression is known as a notation. An arithmetic expression can be written in three different but equivalent notations, i.e., without changing the essence or output of an expression. These notations are − Infix Notation Prefix (Polish) Notation Postfix (Reverse-Polish) Notation These notations are named as how they use operator in expression. We shall learn the same here in this chapter. InfixNotation We write expression in infix notation, e.g. a-b+c, where operators are used in-between operands. It is easy for us humans to read, write, and speak in infix notation but the same does not go well with computing devices. An algorithm to process infix notation could be difficult and costly in terms of time and space consumption. PrefixNotation In this notation, operator is prefixed to operands, i.e. operator is written ahead of operands. For example, +ab. This is equivalent to its infix notation a+b. Prefix notation is also known as Polish Notation. PostfixNotation This notation style is known as Reversed Polish Notation. In this notation style, the operator is postfixed to the operands i.e., the operator is written after the operands. For example, ab+. This is equivalent to its infix notation a+b. The following table briefly tries to show the difference in all three notations − Sr. No. Infix Notation Prefix Notation Postfix Notation 1 a + b + a b a b + 2 (a + b) * c * + a b c a b + c * 3 a * (b + c) * a + b c a b c + * 4 a / b + c / d + / a b / c d a b / c d / + 14. Expression Parsing
- 95. Data Structures & Algorithms 86 5 (a + b) * (c + d) * + a b + c d a b + c d + * 6 ((a + b) * c) - d - * + a b c d a b + c * d - ParsingExpressions As we have discussed, it is not a very efficient way to design an algorithm or program to parse infix notations. Instead, these infix notations are first converted into either postfix or prefix notations and then computed. To parse any arithmetic expression, we need to take care of operator precedence and associativity also. Precedence When an operand is in between two different operators, which operator will take the operand first, is decided by the precedence of an operator over others. For example − As multiplication operation has precedence over addition, b * c will be evaluated first. A table of operator precedence is provided later. Associativity Associativity describes the rule where operators with the same precedence appear in an expression. For example, in expression a+b−c, both + and – have the same precedence, then which part of the expression will be evaluated first, is determined by associativity of those operators. Here, both + and − are left associative, so the expression will be evaluated as (a+b)−c. Precedence and associativity determines the order of evaluation of an expression. Following is an operator precedence and associativity table (highest to lowest) − Sr. No. Operator Precedence Associativity 1 Exponentiation ^ Highest Right Associative 2 Multiplication ( * ) & Division ( / ) Second Highest Left Associative 3 Addition ( + ) & Subtraction ( − ) Lowest Left Associative The above table shows the default behavior of operators. At any point of time in expression evaluation, the order can be altered by using parenthesis. For example −
- 96. Data Structures & Algorithms 87 In a+b*c, the expression part b*c will be evaluated first, with multiplication as precedence over addition. We here use parenthesis for a+b to be evaluated first, like (a+b)*c. PostfixEvaluationAlgorithm We shall now look at the algorithm on how to evaluate postfix notation − Step 1 − scan the expression from left to right Step 2 − if it is an operand push it to stack Step 3 − if it is an operator pull operand from stack and perform operation Step 4 − store the output of step 3, back to stack Step 5 − scan the expression until all operands are consumed Step 6 − pop the stack and perform operation To see the implementation in C programming language, please click here ExpressionParsingUsingStack Infix notation is easier for humans to read and understand whereas for electronic machines like computers, postfix is the best form of expression to parse. We shall see here a program to convert and evaluate infix notation to postfix notation − #include<stdio.h> #include<string.h> //char stack char stack[25]; int top = -1; void push(char item) { stack[++top] = item; } char pop() { return stack[top--]; }
- 97. Data Structures & Algorithms 88 //returns precedence of operators int precedence(char symbol) { switch(symbol) { case '+': case '-': return 2; break; case '*': case '/': return 3; break; case '^': return 4; break; case '(': case ')': case '#': return 1; break; } } //check whether the symbol is operator? int isOperator(char symbol) { switch(symbol) { case '+': case '-': case '*': case '/': case '^': case '(': case ')': return 1; break;
- 98. Data Structures & Algorithms 89 default: return 0; } } //converts infix expression to postfix void convert(char infix[],char postfix[]) { int i,symbol,j = 0; stack[++top] = '#'; for(i = 0;i<strlen(infix);i++) { symbol = infix[i]; if(isOperator(symbol) == 0) { postfix[j] = symbol; j++; } else { if(symbol == '(') { push(symbol); }else { if(symbol == ')') { while(stack[top] != '(') { postfix[j] = pop(); j++; } pop();//pop out (. } else { if(precedence(symbol)>precedence(stack[top])) { push(symbol); }else { while(precedence(symbol)<=precedence(stack[top])) { postfix[j] = pop(); j++; }
- 99. Data Structures & Algorithms 90 push(symbol); } } } } } while(stack[top] != '#') { postfix[j] = pop(); j++; } postfix[j]='0';//null terminate string. } //int stack int stack_int[25]; int top_int = -1; void push_int(int item) { stack_int[++top_int] = item; } char pop_int() { return stack_int[top_int--]; } //evaluates postfix expression int evaluate(char *postfix){ char ch; int i = 0,operand1,operand2; while( (ch = postfix[i++]) != '0') { if(isdigit(ch)) {
- 100. Data Structures & Algorithms 91 push_int(ch-'0'); // Push the operand }else { //Operator,pop two operands operand2 = pop_int(); operand1 = pop_int(); switch(ch) { case '+': push_int(operand1+operand2); break; case '-': push_int(operand1-operand2); break; case '*': push_int(operand1*operand2); break; case '/': push_int(operand1/operand2); break; } } } return stack_int[top_int]; } void main() { char infix[25] = "1*(2+3)",postfix[25]; convert(infix,postfix); printf("Infix expression is: %sn" , infix); printf("Postfix expression is: %sn" , postfix); printf("Evaluated expression is: %dn" , evaluate(postfix)); }
- 101. Data Structures & Algorithms 92 If we compile and run the above program, it will produce the following result − Infix expression is: 1*(2+3) Postfix expression is: 123+* Result is: 5
- 102. Data Structures & Algorithms 93 Queue is an abstract data structure, somewhat similar to Stacks. Unlike stacks, a queue is open at both its ends. One end is always used to insert data (enqueue) and the other is used to remove data (dequeue). Queue follows First-In-First-Out methodology, i.e., the data item stored first will be accessed first. A real-world example of queue can be a single-lane one-way road, where the vehicle enters first, exits first. More real-world examples can be seen as queues at the ticket windows and bus-stops. QueueRepresentation As we now understand that in queue, we access both ends for different reasons. The following diagram given below tries to explain queue representation as data structure − As in stacks, a queue can also be implemented using Arrays, Linked-lists, Pointers and Structures. For the sake of simplicity, we shall implement queues using one-dimensional array. BasicOperations Queue operations may involve initializing or defining the queue, utilizing it, and then completely erasing it from the memory. Here we shall try to understand the basic operations associated with queues − enqueue() − add (store) an item to the queue. dequeue() − remove (access) an item from the queue. 15. Queue
- 103. Data Structures & Algorithms 94 Few more functions are required to make the above-mentioned queue operation efficient. These are − peek() − Gets the element at the front of the queue without removing it. isfull() − Checks if the queue is full. isempty() − Checks if the queue is empty. In queue, we always dequeue (or access) data, pointed by front pointer and while enqueing (or storing) data in the queue we take help of rear pointer. Let's first learn about supportive functions of a queue − peek() This function helps to see the data at the front of the queue. The algorithm of peek() function is as follows − begin procedure peek return queue[front] end procedure Implementation of peek() function in C programming language − int peek() { return queue[front]; } isfull() As we are using single dimension array to implement queue, we just check for the rear pointer to reach at MAXSIZE to determine that the queue is full. In case we maintain the queue in a circular linked-list, the algorithm will differ. Algorithm of isfull() function − begin procedure isfull if rear equals to MAXSIZE return true else
- 104. Data Structures & Algorithms 95 return false endif end procedure Implementation of isfull() function in C programming language − bool isfull() { if(rear == MAXSIZE - 1) return true; else return false; } isempty() Algorithm of isempty() function − begin procedure isempty if front is less than MIN OR front is greater than rear return true else return false endif end procedure If the value of front is less than MIN or 0, it tells that the queue is not yet initialized, hence empty. Here's the C programming code − bool isempty() { if(front < 0 || front > rear) return true; else return false; }
- 105. Data Structures & Algorithms 96 EnqueueOperation Queues maintain two data pointers, front and rear. Therefore, its operations are comparatively difficult to implement than that of stacks. The following steps should be taken to enqueue (insert) data into a queue − Step 1 − Check if the queue is full. Step 2 − If the queue is full, produce overflow error and exit. Step 3 − If the queue is not full, increment rear pointer to point the next empty space. Step 4 − Add data element to the queue location, where the rear is pointing. Step 5 − Return success. Sometimes, we also check to see if a queue is initialized or not, to handle any unforeseen situations.
- 106. Data Structures & Algorithms 97 Algorithm for enqueue Operation procedure enqueue(data) if queue is full return overflow endif rear ← rear + 1 queue[rear] ← data return true end procedure Implementation of enqueue() in C programming language − int enqueue(int data) if(isfull()) return 0; rear = rear + 1; queue[rear] = data; return 1; end procedure DequeueOperation Accessing data from the queue is a process of two tasks − access the data where front is pointing and remove the data after access. The following steps are taken to perform dequeue operation − Step 1 − Check if the queue is empty. Step 2 − If the queue is empty, produce underflow error and exit. Step 3 − If the queue is not empty, access the data where front is pointing. Step 4 − Increment front pointer to point to the next available data element. Step 5 − Return success.
- 107. Data Structures & Algorithms 98 Algorithm for dequeue Operation procedure dequeue if queue is empty return underflow end if data = queue[front] front ← front + 1 return true end procedure Implementation of dequeue() in C programming language − int dequeue() { if(isempty()) return 0; int data = queue[front]; front = front + 1; return data; } For a complete Queue program in C programming language, please click here.
- 108. Data Structures & Algorithms 99 QueuePrograminC We shall see the stack implementation in C programming language here. You can try the program by clicking on the Try-it button. To learn the theory aspect of stacks, click on visit previous page. Implementation in C #include <stdio.h> #include <string.h> #include <stdlib.h> #include <stdbool.h> #define MAX 6 int intArray[MAX]; int front = 0; int rear = -1; int itemCount = 0; int peek(){ return intArray[front]; } bool isEmpty(){ return itemCount == 0; } bool isFull(){ return itemCount == MAX; } int size(){ return itemCount; } void insert(int data){ if(!isFull()){
- 109. Data Structures & Algorithms 100 if(rear == MAX-1){ rear = -1; } intArray[++rear] = data; itemCount++; } } int removeData(){ int data = intArray[front++]; if(front == MAX){ front = 0; } itemCount--; return data; } int main() { /* insert 5 items */ insert(3); insert(5); insert(9); insert(1); insert(12); // front : 0 // rear : 4 // ------------------ // index : 0 1 2 3 4 // ------------------ // queue : 3 5 9 1 12 insert(15); // front : 0 // rear : 5
- 110. Data Structures & Algorithms 101 // --------------------- // index : 0 1 2 3 4 5 // --------------------- // queue : 3 5 9 1 12 15 if(isFull()){ printf("Queue is full!n"); } // remove one item int num = removeData(); printf("Element removed: %dn",num); // front : 1 // rear : 5 // ------------------- // index : 1 2 3 4 5 // ------------------- // queue : 5 9 1 12 15 // insert more items insert(16); // front : 1 // rear : -1 // ---------------------- // index : 0 1 2 3 4 5 // ---------------------- // queue : 16 5 9 1 12 15 // As queue is full, elements will not be inserted. insert(17); insert(18); // ---------------------- // index : 0 1 2 3 4 5 // ----------------------
- 111. Data Structures & Algorithms 102 // queue : 16 5 9 1 12 15 printf("Element at front: %dn",peek()); printf("----------------------n"); printf("index : 5 4 3 2 1 0n"); printf("----------------------n"); printf("Queue: "); while(!isEmpty()){ int n = removeData(); printf("%d ",n); } } If we compile and run the above program, it will produce the following result − Queue is full! Element removed: 3 Element at front: 5 ---------------------- index : 5 4 3 2 1 0 ---------------------- Queue: 5 9 1 12 15 16
- 112. Data Structures & Algorithms 103 Searching Techniques
- 113. Data Structures & Algorithms 104 Linear search is a very simple search algorithm. In this type of search, a sequential search is made over all items one by one. Every item is checked and if a match is found then that particular item is returned, otherwise the search continues till the end of the data collection. Algorithm Linear Search ( Array A, Value x) Step 1: Set i to 1 Step 2: if i > n then go to step 7 Step 3: if A[i] = x then go to step 6 Step 4: Set i to i + 1 Step 5: Go to Step 2 Step 6: Print Element x Found at index i and go to step 8 Step 7: Print element not found Step 8: Exit Pseudocode procedure linear_search (list, value) for each item in the list if match item == value return the item's location 16. Linear Search
- 114. Data Structures & Algorithms 105 end if end for end procedure To know about linear search implementation in C programming language, please click- here. LinearSearchPrograminC Here we present the implementation of linear search in C programming language. The output of the program is given after the code. Linear Search Program #include <stdio.h> #define MAX 20 // array of items on which linear search will be conducted. int intArray[MAX] = {1,2,3,4,6,7,9,11,12,14,15,16,17,19,33,34,43,45,55,66}; void printline(int count){ int i; for(i = 0;i <count-1;i++){ printf("="); } printf("=n"); } // this method makes a linear search. int find(int data){ int comparisons = 0; int index = -1; int i;
- 115. Data Structures & Algorithms 106 // navigate through all items for(i = 0;i<MAX;i++){ // count the comparisons made comparisons++; // if data found, break the loop if(data == intArray[i]){ index = i; break; } } printf("Total comparisons made: %d", comparisons); return index; } void display(){ int i; printf("["); // navigate through all items for(i = 0;i<MAX;i++){ printf("%d ",intArray[i]); } printf("]n"); } main(){ printf("Input Array: "); display(); printline(50);
- 116. Data Structures & Algorithms 107 //find location of 1 int location = find(55); // if element was found if(location != -1) printf("nElement found at location: %d" ,(location+1)); else printf("Element not found."); } If we compile and run the above program, it will produce the following result − Input Array: [1 2 3 4 6 7 9 11 12 14 15 16 17 19 33 34 43 45 55 66 ] ================================================== Total comparisons made: 19 Element found at location: 19
- 117. Data Structures & Algorithms 108 Binary search is a fast search algorithm with run-time complexity of Ο(log n). This search algorithm works on the principle of divide and conquer. For this algorithm to work properly, the data collection should be in the sorted form. Binary search looks for a particular item by comparing the middle most item of the collection. If a match occurs, then the index of item is returned. If the middle item is greater than the item, then the item is searched in the sub-array to the right of the middle item. Otherwise, the item is searched for in the sub-array to the left of the middle item. This process continues on the sub-array as well until the size of the subarray reduces to zero. HowBinarySearchWorks? For a binary search to work, it is mandatory for the target array to be sorted. We shall learn the process of binary search with a pictorial example. The following is our sorted array and let us assume that we need to search the location of value 31 using binary search. First, we shall determine half of the array by using this formula − mid = low + (high - low) / 2 Here it is, 0 + (9 - 0 ) / 2 = 4 (integer value of 4.5). So, 4 is the mid of the array. Now we compare the value stored at location 4, with the value being searched, i.e. 31. We find that the value at location 4 is 27, which is not a match. As the value is greater than 27 and we have a sorted array, so we also know that the target value must be in the upper portion of the array. 17. Binary Search
- 118. Data Structures & Algorithms 109 We change our low to mid + 1 and find the new mid value again. low = mid + 1 mid = low + (high - low) / 2 Our new mid is 7 now. We compare the value stored at location 7 with our target value 31. The value stored at location 7 is not a match, rather it is less than what we are looking for. So, the value must be in the lower part from this location. Hence, we calculate the mid again. This time it is 5. We compare the value stored at location 5 with our target value. We find that it is a match. We conclude that the target value 31 is stored at location 5. Binary search halves the searchable items and thus reduces the count of comparisons to be made to very less numbers.
- 119. Data Structures & Algorithms 110 Pseudocode The pseudocode of binary search algorithms should look like this − Procedure binary_search A ← sorted array n ← size of array x ← value ot be searched Set lowerBound = 1 Set upperBound = n while x not found if upperBound < lowerBound EXIT: x does not exists. set midPoint = lowerBound + ( upperBound - lowerBound ) / 2 if A[midPoint] < x set lowerBound = midPoint + 1 if A[midPoint] > x set upperBound = midPoint - 1 if A[midPoint] = x EXIT: x found at location midPoint end while end procedure To know about binary search implementation using array in C programming language, please click here.
- 120. Data Structures & Algorithms 111 BinarySearchPrograminC Binary search is a fast search algorithm with run-time complexity of Ο(log n). This search algorithm works on the principle of divide and conquer. For this algorithm to work properly, the data collection should be in a sorted form. Implementation in C #include <stdio.h> #define MAX 20 // array of items on which linear search will be conducted. int intArray[MAX] = {1,2,3,4,6,7,9,11,12,14,15,16,17,19,33,34,43,45,55,66}; void printline(int count){ int i; for(i = 0;i <count-1;i++){ printf("="); } printf("=n"); } int find(int data){ int lowerBound = 0; int upperBound = MAX -1; int midPoint = -1; int comparisons = 0; int index = -1; while(lowerBound <= upperBound){ printf("Comparison %dn" , (comparisons +1) ) ; printf("lowerBound : %d, intArray[%d] = %dn", lowerBound,lowerBound,intArray[lowerBound]); printf("upperBound : %d, intArray[%d] = %dn", upperBound,upperBound,intArray[upperBound]);
- 121. Data Structures & Algorithms 112 comparisons++; // compute the mid point // midPoint = (lowerBound + upperBound) / 2; midPoint = lowerBound + (upperBound - lowerBound) / 2; // data found if(intArray[midPoint] == data){ index = midPoint; break; }else { // if data is larger if(intArray[midPoint] < data){ // data is in upper half lowerBound = midPoint + 1; } // data is smaller else{ // data is in lower half upperBound = midPoint -1; } } } printf("Total comparisons made: %d" , comparisons); return index; } void display(){ int i; printf("["); // navigate through all items for(i = 0;i<MAX;i++){ printf("%d ",intArray[i]); }
- 122. Data Structures & Algorithms 113 printf("]n"); } main(){ printf("Input Array: "); display(); printline(50); //find location of 1 int location = find(55); // if element was found if(location != -1) printf("nElement found at location: %d" ,(location+1)); else printf("nElement not found."); } If we compile and run the above program, it will produce the following result − Input Array: [1 2 3 4 6 7 9 11 12 14 15 16 17 19 33 34 43 45 55 66 ] ================================================== Comparison 1 lowerBound : 0, intArray[0] = 1 upperBound : 19, intArray[19] = 66 Comparison 2 lowerBound : 10, intArray[10] = 15 upperBound : 19, intArray[19] = 66 Comparison 3 lowerBound : 15, intArray[15] = 34 upperBound : 19, intArray[19] = 66 Comparison 4 lowerBound : 18, intArray[18] = 55 upperBound : 19, intArray[19] = 66 Total comparisons made: 4 Element found at location: 19
- 123. Data Structures & Algorithms 114
- 124. Data Structures & Algorithms 115 Interpolation search is an improved variant of binary search. This search algorithm works on the probing position of the required value. For this algorithm to work properly, the data collection should be in a sorted form and equally distributed. Binary search has a huge advantage of time complexity over linear search. Linear search has worst-case complexity of Ο(n) whereas binary search has Ο(log n). There are cases where the location of target data may be known in advance. For example, in case of a telephone directory, if we want to search the telephone number of Morphius. Here, linear search and even binary search will seem slow as we can directly jump to memory space where the names start from 'M' are stored. PositioninginBinarySearch In binary search, if the desired data is not found then the rest of the list is divided in two parts, lower and higher. The search is carried out in either of them. Even when the data is sorted, binary search does not take advantage to probe the position of the desired data. 18. Interpolation Search
- 125. Data Structures & Algorithms 116 PositionProbinginInterpolationSearch Interpolation search finds a particular item by computing the probe position. Initially, the probe position is the position of the middle most item of the collection. If a match occurs, then the index of the item is returned. To split the list into two parts, we use the following method − mid = Lo + ((Hi - Lo) / (A[Hi] - A[Lo])) * (X - A[Lo]) where − A = list Lo = Lowest index of the list Hi = Highest index of the list A[n] = Value stored at index n in the list If the middle item is greater than the item, then the probe position is again calculated in the sub-array to the right of the middle item. Otherwise, the item is searched in the sub- array to the left of the middle item. This process continues on the sub-array as well until the size of subarray reduces to zero. Runtime complexity of interpolation search algorithm is Ο(log (log n)) as compared to Ο(log n) of BST in favorable situations. Algorithm As it is an improvisation of the existing BST algorithm, we are mentioning the steps to search the 'target' data value index, using position probing − Step 1 − Start searching data from middle of the list. Step 2 − If it is a match, return the index of the item, and exit. Step 3 − If it is not a match, probe position. Step 4 − Divide the list using probing formula and find the new middle. Step 5 − If data is greater than middle, search in higher sub-list. Step 6 − If data is smaller than middle, search in lower sub-list. Step 7 − Repeat until match.
- 126. Data Structures & Algorithms 117 Pseudocode A → Array list N → Size of A X → Target Value Procedure Interpolation_Search() Set Lo → 0 Set Mid → -1 Set Hi → N-1 While X does not match if Lo equals to Hi OR A[Lo] equals to A[Hi] EXIT: Failure, Target not found end if Set Mid = Lo + ((Hi - Lo) / (A[Hi] - A[Lo])) * (X - A[Lo]) if A[Mid] = X EXIT: Success, Target found at Mid else if A[Mid] < X Set Lo to Mid+1 else if A[Mid] > X Set Hi to Mid-1 end if end if End While End Procedure To know about the implementation of interpolation search in C programming language, click here.
- 127. Data Structures & Algorithms 118 InterpolationSearchPrograminC Interpolation search is an improved variant of binary search. This search algorithm works on the probing position of the required value. For this algorithm to work properly, the data collection should be in sorted and equally distributed form. It's runtime complexity is log2(log2 n). Implementation in C #include<stdio.h> #define MAX 10 // array of items on which linear search will be conducted. int list[MAX] = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44 }; int find(int data) { int lo = 0; int hi = MAX - 1; int mid = -1; int comparisons = 1; int index = -1; while(lo <= hi) { printf("nComparison %d n" , comparisons ) ; printf("lo : %d, list[%d] = %dn", lo, lo, list[lo]); printf("hi : %d, list[%d] = %dn", hi, hi, list[hi]); comparisons++; // probe the mid point mid = lo + (((double)(hi - lo) / (list[hi] - list[lo])) * (data - list[lo])); printf("mid = %dn",mid); // data found if(list[mid] == data) { index = mid; break; }else {
- 128. Data Structures & Algorithms 119 if(list[mid] < data) { // if data is larger, data is in upper half lo = mid + 1; }else { // if data is smaller, data is in lower half hi = mid - 1; } } } printf("nTotal comparisons made: %d", --comparisons); return index; } int main() { //find location of 33 int location = find(33); // if element was found if(location != -1) printf("nElement found at location: %d" ,(location+1)); else printf("Element not found."); return 0; } If we compile and run the above program, it will produce the following result − Comparison 1 lo : 0, list[0] = 10 hi : 9, list[9] = 44 mid = 6 Total comparisons made: 1 Element found at location: 7 You can change the search value and execute the program to test it.
- 129. Data Structures & Algorithms 120 Hash Table is a data structure which stores data in an associative manner. In a hash table, data is stored in an array format, where each data value has its own unique index value. Access of data becomes very fast if we know the index of the desired data. Thus, it becomes a data structure in which insertion and search operations are very fast irrespective of the size of the data. Hash Table uses an array as a storage medium and uses hash technique to generate an index where an element is to be inserted or is to be located from. Hashing Hashing is a technique to convert a range of key values into a range of indexes of an array. We're going to use modulo operator to get a range of key values. Consider an example of hash table of size 20, and the following items are to be stored. Item are in the (key,value) format. (1,20) (2,70) (42,80) (4,25) (12,44) (14,32) (17,11) (13,78) (37,98) 19. Hash Table
- 130. Data Structures & Algorithms 121 Sr. No. Key Hash Array Index 1 1 1 % 20 = 1 1 2 2 2 % 20 = 2 2 3 42 42 % 20 = 2 2 4 4 4 % 20 = 4 4 5 12 12 % 20 = 12 12 6 14 14 % 20 = 14 14 7 17 17 % 20 = 17 17 8 13 13 % 20 = 13 13 9 37 37 % 20 = 17 17 LinearProbing As we can see, it may happen that the hashing technique is used to create an already used index of the array. In such a case, we can search the next empty location in the array by looking into the next cell until we find an empty cell. This technique is called linear probing. Sr. No. Key Hash Array Index After Linear Probing, Array Index 1 1 1 % 20 = 1 1 1 2 2 2 % 20 = 2 2 2 3 42 42 % 20 = 2 2 3 4 4 4 % 20 = 4 4 4 5 12 12 % 20 = 12 12 12 6 14 14 % 20 = 14 14 14
- 131. Data Structures & Algorithms 122 7 17 17 % 20 = 17 17 17 8 13 13 % 20 = 13 13 13 9 37 37 % 20 = 17 17 18 BasicOperations Following are the basic primary operations of a hash table. Search − Searches an element in a hash table. Insert − inserts an element in a hash table. Delete − Deletes an element from a hash table. DataItem Define a data item having some data and key, based on which the search is to be conducted in a hash table. struct DataItem { int data; int key; }; HashMethod Define a hashing method to compute the hash code of the key of the data item. int hashCode(int key){ return key % SIZE; } SearchOperation Whenever an element is to be searched, compute the hash code of the key passed and locate the element using that hash code as index in the array. Use linear probing to get the element ahead if the element is not found at the computed hash code.
- 132. Data Structures & Algorithms 123 struct DataItem *search(int key){ //get the hash int hashIndex = hashCode(key); //move in array until an empty while(hashArray[hashIndex] != NULL){ if(hashArray[hashIndex]->key == key) return hashArray[hashIndex]; //go to next cell ++hashIndex; //wrap around the table hashIndex %= SIZE; } return NULL; } InsertOperation Whenever an element is to be inserted, compute the hash code of the key passed and locate the index using that hash code as an index in the array. Use linear probing for empty location, if an element is found at the computed hash code. void insert(int key,int data){ struct DataItem *item = (struct DataItem*) malloc(sizeof(struct DataItem)); item->data = data; item->key = key; //get the hash int hashIndex = hashCode(key); //move in array until an empty or deleted cell while(hashArray[hashIndex] != NULL && hashArray[hashIndex]->key != -1){ //go to next cell ++hashIndex;
- 133. Data Structures & Algorithms 124 //wrap around the table hashIndex %= SIZE; } hashArray[hashIndex] = item; } DeleteOperation Whenever an element is to be deleted, compute the hash code of the key passed and locate the index using that hash code as an index in the array. Use linear probing to get the element ahead if an element is not found at the computed hash code. When found, store a dummy item there to keep the performance of the hash table intact. struct DataItem* delete(struct DataItem* item){ int key = item->key; //get the hash int hashIndex = hashCode(key); //move in array until an empty while(hashArray[hashIndex] !=NULL){ if(hashArray[hashIndex]->key == key){ struct DataItem* temp = hashArray[hashIndex]; //assign a dummy item at deleted position hashArray[hashIndex] = dummyItem; return temp; } //go to next cell ++hashIndex; //wrap around the table hashIndex %= SIZE; } return NULL; }
- 134. Data Structures & Algorithms 125 To know about hash implementation in C programming language, please click here. HashTablePrograminC Hash Table is a data structure which stores data in an associative manner. In hash table, the data is stored in an array format where each data value has its own unique index value. Access of data becomes very fast, if we know the index of the desired data. Implementation in C #include <stdio.h> #include <string.h> #include <stdlib.h> #include <stdbool.h> #define SIZE 20 struct DataItem { int data; int key; }; struct DataItem* hashArray[SIZE]; struct DataItem* dummyItem; struct DataItem* item; int hashCode(int key){ return key % SIZE; } struct DataItem *search(int key){ //get the hash int hashIndex = hashCode(key); //move in array until an empty while(hashArray[hashIndex] != NULL){ if(hashArray[hashIndex]->key == key) return hashArray[hashIndex];
- 135. Data Structures & Algorithms 126 //go to next cell ++hashIndex; //wrap around the table hashIndex %= SIZE; } return NULL; } void insert(int key,int data){ struct DataItem *item = (struct DataItem*) malloc(sizeof(struct DataItem)); item->data = data; item->key = key; //get the hash int hashIndex = hashCode(key); //move in array until an empty or deleted cell while(hashArray[hashIndex] != NULL && hashArray[hashIndex]->key != -1){ //go to next cell ++hashIndex; //wrap around the table hashIndex %= SIZE; } hashArray[hashIndex] = item; } struct DataItem* delete(struct DataItem* item){ int key = item->key; //get the hash
- 136. Data Structures & Algorithms 127 int hashIndex = hashCode(key); //move in array until an empty while(hashArray[hashIndex] != NULL){ if(hashArray[hashIndex]->key == key){ struct DataItem* temp = hashArray[hashIndex]; //assign a dummy item at deleted position hashArray[hashIndex] = dummyItem; return temp; } //go to next cell ++hashIndex; //wrap around the table hashIndex %= SIZE; } return NULL; } void display(){ int i = 0; for(i = 0; i<SIZE; i++) { if(hashArray[i] != NULL) printf(" (%d,%d)",hashArray[i]->key,hashArray[i]->data); else printf(" ~~ "); } printf("n"); }
- 137. Data Structures & Algorithms 128 int main(){ dummyItem = (struct DataItem*) malloc(sizeof(struct DataItem)); dummyItem->data = -1; dummyItem->key = -1; insert(1, 20); insert(2, 70); insert(42, 80); insert(4, 25); insert(12, 44); insert(14, 32); insert(17, 11); insert(13, 78); insert(37, 97); display(); item = search(37); if(item != NULL){ printf("Element found: %dn", item->data); }else { printf("Element not foundn"); } delete(item); item = search(37); if(item != NULL){ printf("Element found: %dn", item->data); }else { printf("Element not foundn"); } }
- 138. Data Structures & Algorithms 129 If we compile and run the above program, it will produce the following result − ~~ (1,20) (2,70) (42,80) (4,25) ~~ ~~ ~~ ~~ ~~ ~~ ~~ (12,44) (13,78) (14,32) ~~ ~~ (17,11) (37,97) ~~ Element found: 97 Element not found
- 139. Data Structures & Algorithms 130 Sorting Techniques
- 140. Data Structures & Algorithms 131 Sorting refers to arranging data in a particular format. Sorting algorithm specifies the way to arrange data in a particular order. Most common orders are in numerical or lexicographical order. The importance of sorting lies in the fact that data searching can be optimized to a very high level, if data is stored in a sorted manner. Sorting is also used to represent data in more readable formats. Following are some of the examples of sorting in real-life scenarios: Telephone Directory – The telephone directory stores the telephone numbers of people sorted by their names, so that the names can be searched easily. Dictionary – The dictionary stores words in an alphabetical order so that searching of any word becomes easy. In-placeSortingandNot-in-placeSorting Sorting algorithms may require some extra space for comparison and temporary storage of few data elements. These algorithms do not require any extra space and sorting is said to happen in-place, or for example, within the array itself. This is called in-place sorting. Bubble sort is an example of in-place sorting. However, in some sorting algorithms, the program requires space which is more than or equal to the elements being sorted. Sorting which uses equal or more space is called not- in-place sorting. Merge-sort is an example of not-in-place sorting. StableandNotStableSorting If a sorting algorithm, after sorting the contents, does not change the sequence of similar content in which they appear, it is called stable sorting. 20. Sorting Algorithm
- 141. Data Structures & Algorithms 132 If a sorting algorithm, after sorting the contents, changes the sequence of similar content in which they appear, it is called unstable sorting. Stability of an algorithm matters when we wish to maintain the sequence of original elements, like in a tuple for example. AdaptiveandNon-AdaptiveSortingAlgorithm A sorting algorithm is said to be adaptive, if it takes advantage of already 'sorted' elements in the list that is to be sorted. That is, while sorting if the source list has some element already sorted, adaptive algorithms will take this into account and will try not to re-order them. A non-adaptive algorithm is one which does not take into account the elements which are already sorted. They try to force every single element to be re-ordered to confirm their sortedness. ImportantTerms Some terms are generally coined while discussing sorting techniques, here is a brief introduction to them − Increasing Order A sequence of values is said to be in increasing order, if the successive element is greater than the previous one. For example, 1, 3, 4, 6, 8, 9 are in increasing order, as every next element is greater than the previous element. Decreasing Order A sequence of values is said to be in decreasing order, if the successive element is less than the current one. For example, 9, 8, 6, 4, 3, 1 are in decreasing order, as every next element is less than the previous element.
- 142. Data Structures & Algorithms 133 Non-Increasing Order A sequence of values is said to be in non-increasing order, if the successive element is less than or equal to its previous element in the sequence. This order occurs when the sequence contains duplicate values. For example, 9, 8, 6, 3, 3, 1 are in non-increasing order, as every next element is less than or equal to (in case of 3) but not greater than any previous element. Non-Decreasing Order A sequence of values is said to be in non-decreasing order, if the successive element is greater than or equal to its previous element in the sequence. This order occurs when the sequence contains duplicate values. For example, 1, 3, 3, 6, 8, 9 are in non-decreasing order, as every next element is greater than or equal to (in case of 3) but not less than the previous one.
- 143. Data Structures & Algorithms 134 Bubble sort is a simple sorting algorithm. This sorting algorithm is comparison-based algorithm in which each pair of adjacent elements is compared and the elements are swapped if they are not in order. This algorithm is not suitable for large data sets as its average and worst case complexity are of O(n2 ) where n is the number of items. HowBubbleSortWorks? We take an unsorted array for our example. Bubble sort takes Ο(n2 ) time so we're keeping it short and precise. Bubble sort starts with very first two elements, comparing them to check which one is greater. In this case, value 33 is greater than 14, so it is already in sorted locations. Next, we compare 33 with 27. We find that 27 is smaller than 33 and these two values must be swapped. 21. Bubble Sort Algorithm
- 144. Data Structures & Algorithms 135 The new array should look like this − Next we compare 33 and 35. We find that both are in already sorted positions. Then we move to the next two values, 35 and 10. We know then that 10 is smaller 35. Hence they are not sorted. We swap these values. We find that we have reached the end of the array. After one iteration, the array should look like this −
- 145. Data Structures & Algorithms 136 To be precise, we are now showing how an array should look like after each iteration. After the second iteration, it should look like this − Notice that after each iteration, at least one value moves at the end. And when there's no swap required, bubble sorts learns that an array is completely sorted. Now we should look into some practical aspects of bubble sort.
- 146. Data Structures & Algorithms 137 Algorithm We assume list is an array of n elements. We further assume that swap function swaps the values of the given array elements. begin BubbleSort(list) for all elements of list if list[i] > list[i+1] swap(list[i], list[i+1]) end if end for return list end BubbleSort Pseudocode We observe in algorithm that Bubble Sort compares each pair of array element unless the whole array is completely sorted in an ascending order. This may cause a few complexity issues like what if the array needs no more swapping as all the elements are already ascending. To ease-out the issue, we use one flag variable swapped which will help us see if any swap has happened or not. If no swap has occurred, i.e. the array requires no more processing to be sorted, it will come out of the loop. Pseudocode of BubbleSort algorithm can be written as follows − procedure bubbleSort( list : array of items ) loop = list.count; for i = 0 to loop-1 do: swapped = false for j = 0 to loop-1 do: /* compare the adjacent elements */ if list[j] > list[j+1] then /* swap them */ swap( list[j], list[j+1] )
- 147. Data Structures & Algorithms 138 swapped = true end if end for /*if no number was swapped that means array is sorted now, break the loop.*/ if(not swapped) then break end if end for end procedure return list Implementation One more issue we did not address in our original algorithm and its improvised pseudocode, is that, after every iteration the highest values settles down at the end of the array. Hence, the next iteration need not include already sorted elements. For this purpose, in our implementation, we restrict the inner loop to avoid already sorted values. To know about bubble sort implementation in C programming language, please click here. BubbleSortPrograminC We shall see the implementation of bubble sort in C programming language here. Implementation in C #include <stdio.h> #include <stdbool.h> #define MAX 10 int list[MAX] = {1,8,4,6,0,3,5,2,7,9}; void display(){ int i; printf("[");
- 148. Data Structures & Algorithms 139 // navigate through all items for(i = 0; i < MAX; i++){ printf("%d ",list[i]); } printf("]n"); } void bubbleSort() { int temp; int i,j; bool swapped = false; // loop through all numbers for(i = 0; i < MAX-1; i++) { swapped = false; // loop through numbers falling ahead for(j = 0; j < MAX-1-i; j++) { printf(" Items compared: [ %d, %d ] ", list[j],list[j+1]); // check if next number is lesser than current no // swap the numbers. // (Bubble up the highest number) if(list[j] > list[j+1]) { temp = list[j]; list[j] = list[j+1]; list[j+1] = temp; swapped = true; printf(" => swapped [%d, %d]n",list[j],list[j+1]); }else { printf(" => not swappedn"); }
- 149. Data Structures & Algorithms 140 } // if no number was swapped that means // array is sorted now, break the loop. if(!swapped) { break; } printf("Iteration %d#: ",(i+1)); display(); } } main(){ printf("Input Array: "); display(); printf("n"); bubbleSort(); printf("nOutput Array: "); display(); } If we compile and run the above program, it will produce the following result − Input Array: [1 8 4 6 0 3 5 2 7 9 ] Items compared: [ 1, 8 ] => not swapped Items compared: [ 8, 4 ] => swapped [4, 8] Items compared: [ 8, 6 ] => swapped [6, 8] Items compared: [ 8, 0 ] => swapped [0, 8] Items compared: [ 8, 3 ] => swapped [3, 8] Items compared: [ 8, 5 ] => swapped [5, 8] Items compared: [ 8, 2 ] => swapped [2, 8] Items compared: [ 8, 7 ] => swapped [7, 8] Items compared: [ 8, 9 ] => not swapped
- 150. Data Structures & Algorithms 141 Iteration 1#: [1 4 6 0 3 5 2 7 8 9 ] Items compared: [ 1, 4 ] => not swapped Items compared: [ 4, 6 ] => not swapped Items compared: [ 6, 0 ] => swapped [0, 6] Items compared: [ 6, 3 ] => swapped [3, 6] Items compared: [ 6, 5 ] => swapped [5, 6] Items compared: [ 6, 2 ] => swapped [2, 6] Items compared: [ 6, 7 ] => not swapped Items compared: [ 7, 8 ] => not swapped Iteration 2#: [1 4 0 3 5 2 6 7 8 9 ] Items compared: [ 1, 4 ] => not swapped Items compared: [ 4, 0 ] => swapped [0, 4] Items compared: [ 4, 3 ] => swapped [3, 4] Items compared: [ 4, 5 ] => not swapped Items compared: [ 5, 2 ] => swapped [2, 5] Items compared: [ 5, 6 ] => not swapped Items compared: [ 6, 7 ] => not swapped Iteration 3#: [1 0 3 4 2 5 6 7 8 9 ] Items compared: [ 1, 0 ] => swapped [0, 1] Items compared: [ 1, 3 ] => not swapped Items compared: [ 3, 4 ] => not swapped Items compared: [ 4, 2 ] => swapped [2, 4] Items compared: [ 4, 5 ] => not swapped Items compared: [ 5, 6 ] => not swapped Iteration 4#: [0 1 3 2 4 5 6 7 8 9 ] Items compared: [ 0, 1 ] => not swapped Items compared: [ 1, 3 ] => not swapped Items compared: [ 3, 2 ] => swapped [2, 3] Items compared: [ 3, 4 ] => not swapped Items compared: [ 4, 5 ] => not swapped Iteration 5#: [0 1 2 3 4 5 6 7 8 9 ] Items compared: [ 0, 1 ] => not swapped Items compared: [ 1, 2 ] => not swapped Items compared: [ 2, 3 ] => not swapped Items compared: [ 3, 4 ] => not swapped Output Array: [0 1 2 3 4 5 6 7 8 9 ]
- 151. Data Structures & Algorithms 142 This is an in-place comparison-based sorting algorithm. Here, a sub-list is maintained which is always sorted. For example, the lower part of an array is maintained to be sorted. An element which is to be 'insert'ed in this sorted sub-list, has to find its appropriate place and then it has to be inserted there. Hence the name, insertion sort. The array is searched sequentially and unsorted items are moved and inserted into the sorted sub-list (in the same array). This algorithm is not suitable for large data sets as its average and worst case complexity are of Ο(n2 ), where n is the number of items. HowInsertionSortWorks? We take an unsorted array for our example. Insertion sort compares the first two elements. It finds that both 14 and 33 are already in ascending order. For now, 14 is in sorted sub- list. Insertion sort moves ahead and compares 33 with 27. And finds that 33 is not in the correct position. 22. Insertion Sort
- 152. Data Structures & Algorithms 143 It swaps 33 with 27. It also checks with all the elements of sorted sub-list. Here we see that the sorted sub-list has only one element 14, and 27 is greater than 14. Hence, the sorted sub-list remains sorted after swapping. By now we have 14 and 27 in the sorted sub-list. Next, it compares 33 with 10. These values are not in a sorted order. So we swap them. However, swapping makes 27 and 10 unsorted. Hence, we swap them too. Again we find 14 and 10 in an unsorted order.
- 153. Data Structures & Algorithms 144 We swap them again. By the end of third iteration, we have a sorted sub-list of 4 items. This process goes on until all the unsorted values are covered in a sorted sub-list. Now we shall see some programming aspects of insertion sort. Algorithm Now we have a bigger picture of how this sorting technique works, so we can derive simple steps by which we can achieve insertion sort. Step 1 − If it is the first element, it is already sorted. return 1; Step 2 − Pick next element Step 3 − Compare with all elements in the sorted sub-list Step 4 − Shift all the elements in the sorted sub-list that is greater than the value to be sorted Step 5 − Insert the value Step 6 − Repeat until list is sorted Pseudocode procedure insertionSort( A : array of items ) int holePosition int valueToInsert for i = 1 to length(A) inclusive do: /* select value to be inserted */ valueToInsert = A[i] holePosition = i
- 154. Data Structures & Algorithms 145 /*locate hole position for the element to be inserted */ while holePosition > 0 and A[holePosition-1] > valueToInsert do: A[holePosition] = A[holePosition-1] holePosition = holePosition -1 end while /* insert the number at hole position */ A[holePosition] = valueToInsert end for end procedure To know about insertion sort implementation in C programming language, please click here. InsertionSortPrograminC This is an in-place comparison-based sorting algorithm. Here, a sub-list is maintained which is always sorted. For example, the lower part of an array is maintained to be sorted. An element which is to be 'insert'ed in this sorted sub-list, has to find its appropriate place and then it is to be inserted there. Hence the name insertion sort. Implementation in C #include <stdio.h> #include <stdbool.h> #define MAX 7 int intArray[MAX] = {4,6,3,2,1,9,7}; void printline(int count){ int i; for(i = 0;i <count-1;i++){ printf("="); }
- 155. Data Structures & Algorithms 146 printf("=n"); } void display(){ int i; printf("["); // navigate through all items for(i = 0;i<MAX;i++){ printf("%d ",intArray[i]); } printf("]n"); } void insertionSort(){ int valueToInsert; int holePosition; int i; // loop through all numbers for(i = 1; i < MAX; i++){ // select a value to be inserted. valueToInsert = intArray[i]; // select the hole position where number is to be inserted holePosition = i; // check if previous no. is larger than value to be inserted while (holePosition > 0 && intArray[holePosition-1] > valueToInsert){ intArray[holePosition] = intArray[holePosition-1]; holePosition--; printf(" item moved : %dn" , intArray[holePosition]); }
- 156. Data Structures & Algorithms 147 if(holePosition != i){ printf(" item inserted : %d, at position : %dn" , valueToInsert,holePosition); // insert the number at hole position intArray[holePosition] = valueToInsert; } printf("Iteration %d#:",i); display(); } } main(){ printf("Input Array: "); display(); printline(50); insertionSort(); printf("Output Array: "); display(); printline(50); } If we compile and run the above program, it will produce the following result − Input Array: [4 6 3 2 1 9 7 ] ================================================== Iteration 1#:[4 6 3 2 1 9 7 ] item moved : 6 item moved : 4 item inserted : 3, at position : 0 Iteration 2#:[3 4 6 2 1 9 7 ] item moved : 6 item moved : 4 item moved : 3 item inserted : 2, at position : 0 Iteration 3#:[2 3 4 6 1 9 7 ] item moved : 6
- 157. Data Structures & Algorithms 148 item moved : 4 item moved : 3 item moved : 2 item inserted : 1, at position : 0 Iteration 4#:[1 2 3 4 6 9 7 ] Iteration 5#:[1 2 3 4 6 9 7 ] item moved : 9 item inserted : 7, at position : 5 Iteration 6#:[1 2 3 4 6 7 9 ] Output Array: [1 2 3 4 6 7 9 ] ==================================================
- 158. Data Structures & Algorithms 149 Selection sort is a simple sorting algorithm. This sorting algorithm is an in-place comparison-based algorithm in which the list is divided into two parts, the sorted part at the left end and the unsorted part at the right end. Initially, the sorted part is empty and the unsorted part is the entire list. The smallest element is selected from the unsorted array and swapped with the leftmost element, and that element becomes a part of the sorted array. This process continues moving unsorted array boundary by one element to the right. This algorithm is not suitable for large data sets as its average and worst case complexities are of O(n2 ), where n is the number of items. HowSelectionSortWorks? Consider the following depicted array as an example. For the first position in the sorted list, the whole list is scanned sequentially. The first position where 14 is stored presently, we search the whole list and find that 10 is the lowest value. So we replace 14 with 10. After one iteration 10, which happens to be the minimum value in the list, appears in the first position of the sorted list. For the second position, where 33 is residing, we start scanning the rest of the list in a linear manner. We find that 14 is the second lowest value in the list and it should appear at the second place. We swap these values. 23. Selection Sort
- 159. Data Structures & Algorithms 150 After two iterations, two least values are positioned at the beginning in a sorted manner. The same process is applied to the rest of the items in the array. Following is a pictorial depiction of the entire sorting process −
- 160. Data Structures & Algorithms 151 Now, let us learn some programming aspects of selection sort. Algorithm Step 1 − Set MIN to location 0 Step 2 − Search the minimum element in the list Step 3 − Swap with value at location MIN Step 4 − Increment MIN to point to next element Step 5 − Repeat until list is sorted Pseudocode procedure selection sort list : array of items n : size of list for i = 1 to n - 1 /* set current element as minimum*/ min = i /* check the element to be minimum */ for j = i+1 to n if list[j] < list[min] then min = j; end if end for /* swap the minimum element with the current element*/ if indexMin != i then swap list[min] and list[i] end if end for end procedure To know about selection sort implementation in C programming language, please click here.
- 161. Data Structures & Algorithms 152 SelectionSortPrograminC Selection sort is a simple sorting algorithm. This sorting algorithm is an in-place comparison-based algorithm in which the list is divided into two parts, the sorted part at the left end and the unsorted part at the right end. Initially, the sorted part is empty and the unsorted part is the entire list. Implementation in C #include <stdio.h> #include <stdbool.h> #define MAX 7 int intArray[MAX] = {4,6,3,2,1,9,7}; void printline(int count){ int i; for(i = 0;i <count-1;i++){ printf("="); } printf("=n"); } void display(){ int i; printf("["); // navigate through all items for(i = 0;i<MAX;i++){ printf("%d ", intArray[i]); }
- 162. Data Structures & Algorithms 153 printf("]n"); } void selectionSort(){ int indexMin,i,j; // loop through all numbers for(i = 0; i < MAX-1; i++){ // set current element as minimum indexMin = i; // check the element to be minimum for(j = i+1;j<MAX;j++){ if(intArray[j] < intArray[indexMin]){ indexMin = j; } } if(indexMin != i){ printf("Items swapped: [ %d, %d ]n" , intArray[i], intArray[indexMin]); // swap the numbers int temp = intArray[indexMin]; intArray[indexMin] = intArray[i]; intArray[i] = temp; } printf("Iteration %d#:",(i+1)); display(); } }
- 163. Data Structures & Algorithms 154 main(){ printf("Input Array: "); display(); printline(50); selectionSort(); printf("Output Array: "); display(); printline(50); } If we compile and run the above program, it will produce the following result − Input Array: [4 6 3 2 1 9 7 ] ================================================== Items swapped: [ 4, 1 ] Iteration 1#:[1 6 3 2 4 9 7 ] Items swapped: [ 6, 2 ] Iteration 2#:[1 2 3 6 4 9 7 ] Iteration 3#:[1 2 3 6 4 9 7 ] Items swapped: [ 6, 4 ] Iteration 4#:[1 2 3 4 6 9 7 ] Iteration 5#:[1 2 3 4 6 9 7 ] Items swapped: [ 9, 7 ] Iteration 6#:[1 2 3 4 6 7 9 ] Output Array: [1 2 3 4 6 7 9 ] ==================================================
- 164. Data Structures & Algorithms 155 Merge sort is a sorting technique based on divide and conquer technique. With worst-case time complexity being Ο(n log n), it is one of the most respected algorithms. Merge sort first divides the array into equal halves and then combines them in a sorted manner. HowMergeSortWorks? To understand merge sort, we take an unsorted array as the following − We know that merge sort first divides the whole array iteratively into equal halves unless the atomic values are achieved. We see here that an array of 8 items is divided into two arrays of size 4. This does not change the sequence of appearance of items in the original. Now we divide these two arrays into halves. We further divide these arrays and we achieve atomic value which can no more be divided. Now, we combine them in exactly the same manner as they were broken down. Please note the color codes given to these lists. We first compare the element for each list and then combine them into another list in a sorted manner. We see that 14 and 33 are in sorted positions. We compare 27 and 10 and in the target list of 2 values we put 10 first, followed by 27. We change the order of 19 and 35 whereas 42 and 44 are placed sequentially. 24. Merge Sort Algorithm
- 165. Data Structures & Algorithms 156 In the next iteration of the combining phase, we compare lists of two data values, and merge them into a list of found data values placing all in a sorted order. After the final merging, the list should look like this − Now we should learn some programming aspects of merge sorting. Algorithm Merge sort keeps on dividing the list into equal halves until it can no more be divided. By definition, if it is only one element in the list, it is sorted. Then, merge sort combines the smaller sorted lists keeping the new list sorted too. Step 1 − if it is only one element in the list it is already sorted, return. Step 2 − divide the list recursively into two halves until it can no more be divided. Step 3 − merge the smaller lists into new list in sorted order. Pseudocode We shall now see the pseudocodes for merge sort functions. As our algorithms point out two main functions − divide & merge. Merge sort works with recursion and we shall see our implementation in the same way. procedure mergesort( var a as array ) if ( n == 1 ) return a var l1 as array = a[0] ... a[n/2] var l2 as array = a[n/2+1] ... a[n] l1 = mergesort( l1 )
- 166. Data Structures & Algorithms 157 l2 = mergesort( l2 ) return merge( l1, l2 ) end procedure procedure merge( var a as array, var b as array ) var c as array while ( a and b have elements ) if ( a[0] > b[0] ) add b[0] to the end of c remove b[0] from b else add a[0] to the end of c remove a[0] from a end if end while while ( a has elements ) add a[0] to the end of c remove a[0] from a end while while ( b has elements ) add b[0] to the end of c remove b[0] from b end while return c end procedure To know about merge sort implementation in C programming language, please click here.
- 167. Data Structures & Algorithms 158 MergeSortPrograminC Merge sort is a sorting technique based on divide and conquer technique. With the worst- case time complexity being Ο(n log n), it is one of the most respected algorithms. Implementation in C We shall see the implementation of merge sort in C programming language here − #include <stdio.h> #define max 10 int a[10] = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44 }; int b[10]; void merging(int low, int mid, int high) { int l1, l2, i; for(l1 = low, l2 = mid + 1, i = low; l1 <= mid && l2 <= high; i++) { if(a[l1] <= a[l2]) b[i] = a[l1++]; else b[i] = a[l2++]; } while(l1 <= mid) b[i++] = a[l1++]; while(l2 <= high) b[i++] = a[l2++]; for(i = low; i <= high; i++) a[i] = b[i]; } void sort(int low, int high) { int mid; if(low < high) {
- 168. Data Structures & Algorithms 159 mid = (low + high) / 2; sort(low, mid); sort(mid+1, high); merging(low, mid, high); }else { return; } } int main() { int i; printf("List before sortingn"); for(i = 0; i <= max; i++) printf("%d ", a[i]); sort(0, max); printf("nList after sortingn"); for(i = 0; i <= max; i++) printf("%d ", a[i]); } If we compile and run the above program, it will produce the following result − List before sorting 10 14 19 26 27 31 33 35 42 44 0 List after sorting 0 10 14 19 26 27 31 33 35 42 44
- 169. Data Structures & Algorithms 160 Shell sort is a highly efficient sorting algorithm and is based on insertion sort algorithm. This algorithm avoids large shifts as in case of insertion sort, if the smaller value is to the far right and has to be moved to the far left. This algorithm uses insertion sort on a widely spread elements, first to sort them and then sorts the less widely spaced elements. This spacing is termed as interval. This interval is calculated based on Knuth's formula as − h = h * 3 + 1 where − h is interval with initial value 1 This algorithm is quite efficient for medium-sized data sets as its average and worst case complexity are of O(n), where n is the number of items. HowShellSortWorks? Let us consider the following example to have an idea of how shell sort works. We take the same array we have used in our previous examples. For our example and ease of understanding, we take the interval of 4. Make a virtual sub-list of all values located at the interval of 4 positions. Here these values are {35, 14}, {33, 19}, {42, 27} and {10, 14} 25. Shell Sort
- 170. Data Structures & Algorithms 161 We compare values in each sub-list and swap them (if necessary) in the original array. After this step, the new array should look like this − Then, we take interval of 2 and this gap generates two sub-lists - {14, 27, 35, 42}, {19, 10, 33, 44} We compare and swap the values, if required, in the original array. After this step, the array should look like this − Finally, we sort the rest of the array using interval of value 1. Shell sort uses insertion sort to sort the array.
- 171. Data Structures & Algorithms 162 Following is the step-by-step depiction −
- 172. Data Structures & Algorithms 163 We see that it required only four swaps to sort the rest of the array. Algorithm Following is the algorithm for shell sort. Step 1 − Initialize the value of h Step 2 − Divide the list into smaller sub-list of equal interval h Step 3 − Sort these sub-lists using insertion sort Step 3 − Repeat until complete list is sorted Pseudocode Following is the pseudocode for shell sort. procedure shellSort() A : array of items /* calculate interval*/ while interval < A.length /3 do: interval = interval * 3 + 1 end while while interval > 0 do: for outer = interval; outer < A.length; outer ++ do: /* select value to be inserted */ valueToInsert = A[outer] inner = outer; /*shift element towards right*/ while inner > interval -1 && A[inner - interval] >= valueToInsert do: A[inner] = A[inner - interval] inner = inner - interval end while
- 173. Data Structures & Algorithms 164 /* insert the number at hole position */ A[inner] = valueToInsert end for /* calculate interval*/ interval = (interval -1) /3; end while end procedure To know about shell sort implementation in C programming language, please click here. ShellSortPrograminC Shell sort is a highly efficient sorting algorithm and is based on insertion sort algorithm. This algorithm avoids large shifts as in case of insertion sort, if the smaller value is to the far right and has to be moved to the far left. Implementation in C #include <stdio.h> #include <stdbool.h> #define MAX 7 int intArray[MAX] = {4,6,3,2,1,9,7}; void printline(int count){ int i; for(i = 0;i <count-1;i++){ printf("="); } printf("=n"); }
- 174. Data Structures & Algorithms 165 void display(){ int i; printf("["); // navigate through all items for(i = 0;i<MAX;i++){ printf("%d ",intArray[i]); } printf("]n"); } void shellSort(){ int inner, outer; int valueToInsert; int interval = 1; int elements = MAX; int i = 0; while(interval <= elements/3) { interval = interval*3 +1; } while(interval > 0) { printf("iteration %d#:",i); display(); for(outer = interval; outer < elements; outer++) { valueToInsert = intArray[outer]; inner = outer; while(inner > interval -1 && intArray[inner - interval] >= valueToInsert) { intArray[inner] = intArray[inner - interval]; inner -=interval; printf(" item moved :%dn",intArray[inner]); }
- 175. Data Structures & Algorithms 166 intArray[inner] = valueToInsert; printf(" item inserted :%d, at position :%dn",valueToInsert,inner); } interval = (interval -1) /3; i++; } } int main() { printf("Input Array: "); display(); printline(50); shellSort(); printf("Output Array: "); display(); printline(50); return 1; } If we compile and run the above program, it will produce the following result − Input Array: [4 6 3 2 1 9 7 ] ================================================== iteration 0#:[4 6 3 2 1 9 7 ] item moved :4 item inserted :1, at position :0 item inserted :9, at position :5 item inserted :7, at position :6 iteration 1#:[1 6 3 2 4 9 7 ] item inserted :6, at position :1 item moved :6 item inserted :3, at position :1 item moved :6
- 176. Data Structures & Algorithms 167 item moved :3 item inserted :2, at position :1 item moved :6 item inserted :4, at position :3 item inserted :9, at position :5 item moved :9 item inserted :7, at position :5 Output Array: [1 2 3 4 6 7 9 ] ==================================================
- 177. Data Structures & Algorithms 168 Quick sort is a highly efficient sorting algorithm and is based on partitioning of array of data into smaller arrays. A large array is partitioned into two arrays one of which holds values smaller than the specified value, say pivot, based on which the partition is made and another array holds values greater than the pivot value. Quick sort partitions an array and then calls itself recursively twice to sort the two resulting subarrays. This algorithm is quite efficient for large-sized data sets as its average and worst case complexity are of O(nlogn), where n is the number of items. PartitioninQuickSort Following animated representation explains how to find the pivot value in an array. The pivot value divides the list into two parts. And recursively, we find the pivot for each sub-lists until all lists contains only one element. QuickSortPivotAlgorithm Based on our understanding of partitioning in quick sort, we will now try to write an algorithm for it, which is as follows. Step 1 − Choose the highest index value has pivot Step 2 − Take two variables to point left and right of the list excluding pivot Step 3 − left points to the low index Step 4 − right points to the high Step 5 − while value at left is less than pivot move right Step 6 − while value at right is greater than pivot move left Step 7 − if both step 5 and step 6 does not match swap left and right Step 8 − if left ≥ right, the point where they met is new pivot 26. Quick Sort
- 178. Data Structures & Algorithms 169 QuickSortPivotPseudocode The pseudocode for the above algorithm can be derived as − function partitionFunc(left, right, pivot) leftPointer = left -1 rightPointer = right while True do while A[++leftPointer] < pivot do //do-nothing end while while rightPointer > 0 && A[--rightPointer] > pivot do //do-nothing end while if leftPointer >= rightPointer break else swap leftPointer,rightPointer end if end while swap leftPointer,right return leftPointer end function QuickSortAlgorithm Using pivot algorithm recursively, we end up with smaller possible partitions. Each partition is then processed for quick sort. We define recursive algorithm for quicksort as follows − Step 1 − Make the right-most index value pivot Step 2 − partition the array using pivot value Step 3 − quicksort left partition recursively Step 4 − quicksort right partition recursively
- 179. Data Structures & Algorithms 170 QuickSortPseudocode To get more into it, let see the pseudocode for quick sort algorithm − procedure quickSort(left, right) if right-left <= 0 return else pivot = A[right] partition = partitionFunc(left, right, pivot) quickSort(left,partition-1) quickSort(partition+1,right) end if end procedure To know about quick sort implementation in C programming language, please click here. QuickSortPrograminC Quick sort is a highly efficient sorting algorithm and is based on partitioning of array of data into smaller arrays. A large array is partitioned into two arrays one of which holds values smaller than the specified value, say pivot, based on which the partition is made and another array holds values greater than the pivot value. Implementation in C #include <stdio.h> #include <stdbool.h> #define MAX 7 int intArray[MAX] = {4,6,3,2,1,9,7}; void printline(int count){ int i; for(i = 0;i <count-1;i++){ printf("="); }
- 180. Data Structures & Algorithms 171 printf("=n"); } void display(){ int i; printf("["); // navigate through all items for(i = 0;i<MAX;i++){ printf("%d ",intArray[i]); } printf("]n"); } void swap(int num1, int num2){ int temp = intArray[num1]; intArray[num1] = intArray[num2]; intArray[num2] = temp; } int partition(int left, int right, int pivot){ int leftPointer = left -1; int rightPointer = right; while(true){ while(intArray[++leftPointer] < pivot){ //do nothing } while(rightPointer > 0 && intArray[--rightPointer] > pivot){ //do nothing } if(leftPointer >= rightPointer){ break; }else{
- 181. Data Structures & Algorithms 172 printf(" item swapped :%d,%dn", intArray[leftPointer],intArray[rightPointer]); swap(leftPointer,rightPointer); } } printf(" pivot swapped :%d,%dn", intArray[leftPointer],intArray[right]); swap(leftPointer,right); printf("Updated Array: "); display(); return leftPointer; } void quickSort(int left, int right){ if(right-left <= 0){ return; }else { int pivot = intArray[right]; int partitionPoint = partition(left, right, pivot); quickSort(left,partitionPoint-1); quickSort(partitionPoint+1,right); } } main(){ printf("Input Array: "); display(); printline(50); quickSort(0,MAX-1); printf("Output Array: "); display(); printline(50); }
- 182. Data Structures & Algorithms 173 If we compile and run the above program, it will produce the following result − Input Array: [4 6 3 2 1 9 7 ] ================================================== pivot swapped :9,7 Updated Array: [4 6 3 2 1 7 9 ] pivot swapped :4,1 Updated Array: [1 6 3 2 4 7 9 ] item swapped :6,2 pivot swapped :6,4 Updated Array: [1 2 3 4 6 7 9 ] pivot swapped :3,3 Updated Array: [1 2 3 4 6 7 9 ] Output Array: [1 2 3 4 6 7 9 ] ==================================================
- 183. Data Structures & Algorithms 174 Graph Data Structure
- 184. Data Structures & Algorithms 175 A graph is a pictorial representation of a set of objects where some pairs of objects are connected by links. The interconnected objects are represented by points termed as vertices, and the links that connect the vertices are called edges. Formally, a graph is a pair of sets (V, E), where V is the set of vertices and E is the set of edges, connecting the pairs of vertices. Take a look at the following graph − In the above graph, V = {a, b, c, d, e} E = {ab, ac, bd, cd, de} GraphDataStructure Mathematical graphs can be represented in data structure. We can represent a graph using an array of vertices and a two-dimensional array of edges. Before we proceed further, let's familiarize ourselves with some important terms − Vertex − Each node of the graph is represented as a vertex. In the following example, the labeled circle represents vertices. Thus, A to G are vertices. We can represent them using an array as shown in the following image. Here A can be identified by index 0. B can be identified using index 1 and so on. 27. Graphs
- 185. Data Structures & Algorithms 176 Edge − Edge represents a path between two vertices or a line between two vertices. In the following example, the lines from A to B, B to C, and so on represents edges. We can use a two-dimensional array to represent an array as shown in the following image. Here AB can be represented as 1 at row 0, column 1, BC as 1 at row 1, column 2 and so on, keeping other combinations as 0. Adjacency − Two node or vertices are adjacent if they are connected to each other through an edge. In the following example, B is adjacent to A, C is adjacent to B, and so on. Path − Path represents a sequence of edges between the two vertices. In the following example, ABCD represents a path from A to D.
- 186. Data Structures & Algorithms 177 BasicOperations Following are the basic primary operations that can be performed on a Graph: Add Vertex − Adds a vertex to the graph. Add Edge − Adds an edge between the two vertices of the graph. Display Vertex − Displays a vertex of the graph. To know more about Graph, please read Graph Theory Tutorial. We shall learn about traversing a graph in the coming chapters.
- 187. Data Structures & Algorithms 178 Depth First Search (DFS) algorithm traverses a graph in a depthward motion and uses a stack to remember to get the next vertex to start a search, when a dead end occurs in any iteration. As in the example given above, DFS algorithm traverses from A to B to C to D first then to E, then to F and lastly to G. It employs the following rules. Rule 1 − Visit the adjacent unvisited vertex. Mark it as visited. Display it. Push it in a stack. Rule 2 − If no adjacent vertex is found, pop up a vertex from the stack. (It will pop up all the vertices from the stack, which do not have adjacent vertices.) Rule 3 − Repeat Rule 1 and Rule 2 until the stack is empty. 28. Depth First Traversal
- 188. Data Structures & Algorithms 179 Steps Traversal Description 1. Initialize the stack. 2. Mark S as visited and put it onto the stack. Explore any unvisited adjacent node from S. We have three nodes and we can pick any of them. For this example, we shall take the node in an alphabetical order. 3. Mark A as visited and put it onto the stack. Explore any unvisited adjacent node from A. Both S and D are adjacent to A but we are concerned for unvisited nodes only.
- 189. Data Structures & Algorithms 180 4. Visit D and mark it as visited and put onto the stack. Here, we have B and C nodes, which are adjacent to D and both are unvisited. However, we shall again choose in an alphabetical order. 5. We choose B, mark it as visited and put onto the stack. Here B does not have any unvisited adjacent node. So, we pop B from the stack. 6. We check the stack top for return to the previous node and check if it has any unvisited nodes. Here, we find D to be on the top of the stack. 7. Only unvisited adjacent node is from D is C now. So we visit C, mark it as visited and put it onto the stack.
- 190. Data Structures & Algorithms 181 As C does not have any unvisited adjacent node so we keep popping the stack until we find a node that has an unvisited adjacent node. In this case, there's none and we keep popping until the stack is empty. To know about the implementation of this algorithm in C programming language, click here. DepthFirstTraversalinC We shall not see the implementation of Depth First Traversal (or Depth First Search) in C programming language. For our reference purpose, we shall follow our example and take this as our graph model − Implementation in C #include <stdio.h> #include <stdlib.h> #include <stdbool.h> #define MAX 5 struct Vertex { char label; bool visited; };
- 191. Data Structures & Algorithms 182 //stack variables int stack[MAX]; int top = -1; //graph variables //array of vertices struct Vertex* lstVertices[MAX]; //adjacency matrix int adjMatrix[MAX][MAX]; //vertex count int vertexCount = 0; //stack functions void push(int item) { stack[++top] = item; } int pop() { return stack[top--]; } int peek() { return stack[top]; } bool isStackEmpty() { return top == -1; }
- 192. Data Structures & Algorithms 183 //graph functions //add vertex to the vertex list void addVertex(char label) { struct Vertex* vertex = (struct Vertex*) malloc(sizeof(struct Vertex)); vertex->label = label; vertex->visited = false; lstVertices[vertexCount++] = vertex; } //add edge to edge array void addEdge(int start,int end) { adjMatrix[start][end] = 1; adjMatrix[end][start] = 1; } //display the vertex void displayVertex(int vertexIndex) { printf("%c ",lstVertices[vertexIndex]->label); } //get the adjacent unvisited vertex int getAdjUnvisitedVertex(int vertexIndex) { int i; for(i = 0; i<vertexCount; i++) { if(adjMatrix[vertexIndex][i] == 1 && lstVertices[i]->visited == false) { return i; } } return -1; }
- 193. Data Structures & Algorithms 184 void depthFirstSearch() { int i; //mark first node as visited lstVertices[0]->visited = true; //display the vertex displayVertex(0); //push vertex index in stack push(0); while(!isStackEmpty()) { //get the unvisited vertex of vertex which is at top of the stack int unvisitedVertex = getAdjUnvisitedVertex(peek()); //no adjacent vertex found if(unvisitedVertex == -1) { pop(); }else { lstVertices[unvisitedVertex]->visited = true; displayVertex(unvisitedVertex); push(unvisitedVertex); } } //stack is empty, search is complete, reset the visited flag for(i = 0;i < vertexCount;i++) { lstVertices[i]->visited = false; } }
- 194. Data Structures & Algorithms 185 int main() { int i, j; for(i = 0; i<MAX; i++) // set adjacency { for(j = 0; j<MAX; j++) // matrix to 0 adjMatrix[i][j] = 0; } addVertex('S'); // 0 addVertex('A'); // 1 addVertex('B'); // 2 addVertex('C'); // 3 addVertex('D'); // 4 addEdge(0, 1); // S - A addEdge(0, 2); // S - B addEdge(0, 3); // S - C addEdge(1, 4); // A - D addEdge(2, 4); // B - D addEdge(3, 4); // C - D printf("Depth First Search: "); depthFirstSearch(); return 0; } If we compile and run the above program, it will produce the following result − Depth First Search: S A D B C
- 195. Data Structures & Algorithms 186 Breadth First Search (BFS) algorithm traverses a graph in a breadthward motion and uses a queue to remember to get the next vertex to start a search, when a dead end occurs in any iteration. As in the example given above, BFS algorithm traverses from A to B to E to F first then to C and G lastly to D. It employs the following rules. Rule 1 − Visit the adjacent unvisited vertex. Mark it as visited. Display it. Insert it in a queue. Rule 2 − If no adjacent vertex is found, remove the first vertex from the queue. Rule 3 − Repeat Rule 1 and Rule 2 until the queue is empty. 29. Breadth First Traversal
- 196. Data Structures & Algorithms 187 Steps Traversal Description 1. Initialize the queue. 2. We start from visiting S (starting node), and mark it as visited. 3. We then see an unvisited adjacent node from S. In this example, we have three nodes but alphabetically we choose A, mark it as visited and enqueue it. 4. Next, the unvisited adjacent node from S is B. We mark it as visited and enqueue it.
- 197. Data Structures & Algorithms 188 5. Next, the unvisited adjacent node from S is C. We mark it as visited and enqueue it. 6. Now, S is left with no unvisited adjacent nodes. So, we dequeue and find A. 7. From A we have D as unvisited adjacent node. We mark it as visited and enqueue it. At this stage, we are left with no unmarked (unvisited) nodes. But as per the algorithm we keep on dequeuing in order to get all unvisited nodes. When the queue gets emptied, the program is over. The implementation of this algorithm in C programming language can be seen here. BreadthFirstTraversalinC We shall not see the implementation of Breadth First Traversal (or Breadth First Search) in C programming language. For our reference purpose, we shall follow our example and take this as our graph model −
- 198. Data Structures & Algorithms 189 Implementation in C #include <stdio.h> #include <stdlib.h> #include <stdbool.h> #define MAX 5 struct Vertex { char label; bool visited; }; //queue variables int queue[MAX]; int rear = -1; int front = 0; int queueItemCount = 0; //graph variables
- 199. Data Structures & Algorithms 190 //array of vertices struct Vertex* lstVertices[MAX]; //adjacency matrix int adjMatrix[MAX][MAX]; //vertex count int vertexCount = 0; //queue functions void insert(int data) { queue[++rear] = data; queueItemCount++; } int removeData() { queueItemCount--; return queue[front++]; } bool isQueueEmpty() { return queueItemCount == 0; } //graph functions //add vertex to the vertex list void addVertex(char label) { struct Vertex* vertex = (struct Vertex*) malloc(sizeof(struct Vertex)); vertex->label = label; vertex->visited = false; lstVertices[vertexCount++] = vertex; }
- 200. Data Structures & Algorithms 191 //add edge to edge array void addEdge(int start,int end) { adjMatrix[start][end] = 1; adjMatrix[end][start] = 1; } //display the vertex void displayVertex(int vertexIndex) { printf("%c ",lstVertices[vertexIndex]->label); } //get the adjacent unvisited vertex int getAdjUnvisitedVertex(int vertexIndex) { int i; for(i = 0; i<vertexCount; i++) { if(adjMatrix[vertexIndex][i] == 1 && lstVertices[i]->visited == false) return i; } return -1; } void breadthFirstSearch() { int i; //mark first node as visited lstVertices[0]->visited = true; //display the vertex displayVertex(0);
- 201. Data Structures & Algorithms 192 //insert vertex index in queue insert(0); int unvisitedVertex; while(!isQueueEmpty()) { //get the unvisited vertex of vertex which is at front of the queue int tempVertex = removeData(); //no adjacent vertex found while((unvisitedVertex = getAdjUnvisitedVertex(tempVertex)) != -1) { lstVertices[unvisitedVertex]->visited = true; displayVertex(unvisitedVertex); insert(unvisitedVertex); } } //queue is empty, search is complete, reset the visited flag for(i = 0;i<vertexCount;i++) { lstVertices[i]->visited = false; } } int main() { int i, j; for(i = 0; i<MAX; i++) // set adjacency { for(j = 0; j<MAX; j++) // matrix to 0 adjMatrix[i][j] = 0; } addVertex('S'); // 0 addVertex('A'); // 1 addVertex('B'); // 2 addVertex('C'); // 3 addVertex('D'); // 4
- 202. Data Structures & Algorithms 193 addEdge(0, 1); // S - A addEdge(0, 2); // S - B addEdge(0, 3); // S - C addEdge(1, 4); // A - D addEdge(2, 4); // B - D addEdge(3, 4); // C - D printf("nBreadth First Search: "); breadthFirstSearch(); return 0; } If we compile and run the above program, it will produce the following result − Breadth First Search: S A B C D
- 203. Data Structures & Algorithms 194 Tree Data Structure
- 204. Data Structures & Algorithms 195 Tree represents the nodes connected by edges. We will discuss binary tree or binary search tree specifically. Binary Tree is a special datastructure used for data storage purposes. A binary tree has a special condition that each node can have a maximum of two children. A binary tree has the benefits of both an ordered array and a linked list as search is as quick as in a sorted array and insertion or deletion operation are as fast as in linked list. ImportantTerms Following are the important terms with respect to tree. Path − Path refers to the sequence of nodes along the edges of a tree. Root – The node at the top of the tree is called root. There is only one root per tree and one path from the root node to any node. Parent − Any node except the root node has one edge upward to a node called parent. Child – The node below a given node connected by its edge downward is called its child node. Leaf – The node which does not have any child node is called the leaf node. Subtree − Subtree represents the descendants of a node. 30. Tree
- 205. Data Structures & Algorithms 196 Visiting − Visiting refers to checking the value of a node when control is on the node. Traversing − Traversing means passing through nodes in a specific order. Levels − Level of a node represents the generation of a node. If the root node is at level 0, then its next child node is at level 1, its grandchild is at level 2, and so on. Keys − Key represents a value of a node based on which a search operation is to be carried out for a node. BinarySearchTreeRepresentation Binary Search tree exhibits a special behavior. A node's left child must have a value less than its parent's value and the node's right child must have a value greater than its parent value. We're going to implement tree using node object and connecting them through references. TreeNode The code to write a tree node would be similar to what is given below. It has a data part and references to its left and right child nodes. struct node { int data; struct node *leftChild; struct node *rightChild; };
- 206. Data Structures & Algorithms 197 In a tree, all nodes share common construct. BSTBasicOperations The basic operations that can be performed on a binary search tree data structure, are the following − Insert − Inserts an element in a tree/create a tree. Search − Searches an element in a tree. Pre-order Traversal − Traverses a tree in a pre-order manner. In-order Traversal − Traverses a tree in an in-order manner. Post-order Traversal − Traverses a tree in a post-order manner. We shall learn creating (inserting into) a tree structure and searching a data item in a tree in this chapter. We shall learn about tree traversing methods in the coming chapter. InsertOperation The very first insertion creates the tree. Afterwards, whenever an element is to be inserted, first locate its proper location. Start searching from the root node, then if the data is less than the key value, search for the empty location in the left subtree and insert the data. Otherwise, search for the empty location in the right subtree and insert the data. Algorithm If root is NULL then create root node return If root exists then compare the data with node.data while until insertion position is located If data is greater than node.data goto right subtree else goto left subtree
- 207. Data Structures & Algorithms 198 endwhile insert data end If Implementation The implementation of insert function should look like this − void insert(int data) { struct node *tempNode = (struct node*) malloc(sizeof(struct node)); struct node *current; struct node *parent; tempNode->data = data; tempNode->leftChild = NULL; tempNode->rightChild = NULL; //if tree is empty, create root node if(root == NULL) { root = tempNode; }else { current = root; parent = NULL; while(1) { parent = current; //go to left of the tree if(data < parent->data) { current = current->leftChild; //insert to the left if(current == NULL) { parent->leftChild = tempNode; return; }
- 208. Data Structures & Algorithms 199 } //go to right of the tree else { current = current->rightChild; //insert to the right if(current == NULL) { parent->rightChild = tempNode; return; } } } } } SearchOperation Whenever an element is to be searched, start searching from the root node, then if the data is less than the key value, search for the element in the left subtree. Otherwise, search for the element in the right subtree. Follow the same algorithm for each node. Algorithm If root.data is equal to search.data return root else while data not found If data is greater than node.data goto right subtree else goto left subtree If data found return node endwhile
- 209. Data Structures & Algorithms 200 return data not found end if The implementation of this algorithm should look like this. struct node* search(int data) { struct node *current = root; printf("Visiting elements: "); while(current->data != data) { if(current != NULL) printf("%d ",current->data); //go to left tree if(current->data > data) { current = current->leftChild; } //else go to right tree else { current = current->rightChild; } //not found if(current == NULL) { return NULL; } return current; } } To know about the implementation of binary search tree data structure, please click here. TreeTraversalinC Traversal is a process to visit all the nodes of a tree and may print their values too. Because, all nodes are connected via edges (links) we always start from the root (head)
- 210. Data Structures & Algorithms 201 node. That is, we cannot random access a node in a tree. There are three ways which we use to traverse a tree − In-order Traversal Pre-order Traversal Post-order Traversal We shall now look at the implementation of tree traversal in C programming language here using the following binary tree − Implementation in C #include <stdio.h> #include <stdlib.h> struct node { int data; struct node *leftChild; struct node *rightChild; }; struct node *root = NULL; void insert(int data) { struct node *tempNode = (struct node*) malloc(sizeof(struct node)); struct node *current; struct node *parent; tempNode->data = data;
- 211. Data Structures & Algorithms 202 tempNode->leftChild = NULL; tempNode->rightChild = NULL; //if tree is empty if(root == NULL) { root = tempNode; }else { current = root; parent = NULL; while(1) { parent = current; //go to left of the tree if(data < parent->data) { current = current->leftChild; //insert to the left if(current == NULL) { parent->leftChild = tempNode; return; } }//go to right of the tree else { current = current->rightChild; //insert to the right if(current == NULL) { parent->rightChild = tempNode; return; } } } } } struct node* search(int data) { struct node *current = root;
- 212. Data Structures & Algorithms 203 printf("Visiting elements: "); while(current->data != data) { if(current != NULL) printf("%d ",current->data); //go to left tree if(current->data > data) { current = current->leftChild; } //else go to right tree else { current = current->rightChild; } //not found if(current == NULL) { return NULL; } } return current; } void pre_order_traversal(struct node* root) { if(root != NULL) { printf("%d ",root->data); pre_order_traversal(root->leftChild); pre_order_traversal(root->rightChild); } } void inorder_traversal(struct node* root) { if(root != NULL) { inorder_traversal(root->leftChild); printf("%d ",root->data); inorder_traversal(root->rightChild);
- 213. Data Structures & Algorithms 204 } } void post_order_traversal(struct node* root) { if(root != NULL) { post_order_traversal(root->leftChild); post_order_traversal(root->rightChild); printf("%d ", root->data); } } int main() { int i; int array[7] = { 27, 14, 35, 10, 19, 31, 42 }; for(i = 0; i < 7; i++) insert(array[i]); i = 31; struct node * temp = search(i); if(temp != NULL) { printf("[%d] Element found.", temp->data); printf("n"); }else { printf("[ x ] Element not found (%d).n", i); } i = 15; temp = search(i); if(temp != NULL) { printf("[%d] Element found.", temp->data); printf("n"); }else { printf("[ x ] Element not found (%d).n", i); }
- 214. Data Structures & Algorithms 205 printf("nPreorder traversal: "); pre_order_traversal(root); printf("nInorder traversal: "); inorder_traversal(root); printf("nPost order traversal: "); post_order_traversal(root); return 0; } If we compile and run the above program, it will produce the following result − Visiting elements: 27 35 [31] Element found. Visiting elements: 27 14 19 [ x ] Element not found (15). Preorder traversal: 27 14 10 19 35 31 42 Inorder traversal: 10 14 19 27 31 35 42 Post order traversal: 10 19 14 31 42 35 27
- 215. Data Structures & Algorithms 206 Traversal is a process to visit all the nodes of a tree and may print their values too. Because, all nodes are connected via edges (links) we always start from the root (head) node. That is, we cannot randomly access a node in a tree. There are three ways which we use to traverse a tree − In-order Traversal Pre-order Traversal Post-order Traversal Generally, we traverse a tree to search or locate a given item or key in the tree or to print all the values it contains. In-orderTraversal In this traversal method, the left subtree is visited first, then the root and later the right sub-tree. We should always remember that every node may represent a subtree itself. If a binary tree is traversed in-order, the output will produce sorted key values in an ascending order. 31. Tree Traversal
- 216. Data Structures & Algorithms 207 We start from A, and following in-order traversal, we move to its left subtree B. B is also traversed in-order. The process goes on until all the nodes are visited. The output of in- order traversal of this tree will be − D → B → E → A → F → C → G Algorithm Until all nodes are traversed − Step 1 − Recursively traverse left subtree. Step 2 − Visit root node. Step 3 − Recursively traverse right subtree. Pre-orderTraversal In this traversal method, the root node is visited first, then the left subtree and finally the right subtree. We start from A, and following pre-order traversal, we first visit A itself and then move to its left subtree B. B is also traversed pre-order. The process goes on until all the nodes are visited. The output of pre-order traversal of this tree will be − A → B → D → E → C → F → G
- 217. Data Structures & Algorithms 208 Algorithm Until all nodes are traversed − Step 1 − Visit root node. Step 2 − Recursively traverse left subtree. Step 3 − Recursively traverse right subtree. Post-orderTraversal In this traversal method, the root node is visited last, hence the name. First we traverse the left subtree, then the right subtree and finally the root node. We start from A, and following pre-order traversal, we first visit the left subtree B. B is also traversed post-order. The process goes on until all the nodes are visited. The output of post-order traversal of this tree will be − D → E → B → F → G → C → A
- 218. Data Structures & Algorithms 209 Algorithm Until all nodes are traversed − Step 1 − Recursively traverse left subtree. Step 2 − Recursively traverse right subtree. Step 3 − Visit root node. To check the C implementation of tree traversing, please click here TreeTraversalinC Traversal is a process to visit all the nodes of a tree and may print their values too. Because, all nodes are connected via edges (links) we always start from the root (head) node. That is, we cannot randomly access a node in a tree. There are three ways which we use to traverse a tree − In-order Traversal Pre-order Traversal Post-order Traversal We shall now see the implementation of tree traversal in C programming language here using the following binary tree −
- 219. Data Structures & Algorithms 210 Implementation in C #include <stdio.h> #include <stdlib.h> struct node { int data; struct node *leftChild; struct node *rightChild; }; struct node *root = NULL; void insert(int data) { struct node *tempNode = (struct node*) malloc(sizeof(struct node)); struct node *current; struct node *parent; tempNode->data = data; tempNode->leftChild = NULL; tempNode->rightChild = NULL; //if tree is empty if(root == NULL) { root = tempNode; }else { current = root; parent = NULL; while(1) { parent = current; //go to left of the tree if(data < parent->data) { current = current->leftChild;
- 220. Data Structures & Algorithms 211 //insert to the left if(current == NULL) { parent->leftChild = tempNode; return; } }//go to right of the tree else { current = current->rightChild; //insert to the right if(current == NULL) { parent->rightChild = tempNode; return; } } } } } struct node* search(int data) { struct node *current = root; printf("Visiting elements: "); while(current->data != data) { if(current != NULL) printf("%d ",current->data); //go to left tree if(current->data > data) { current = current->leftChild; } //else go to right tree else { current = current->rightChild; } //not found
- 221. Data Structures & Algorithms 212 if(current == NULL) { return NULL; } } return current; } void pre_order_traversal(struct node* root) { if(root != NULL) { printf("%d ",root->data); pre_order_traversal(root->leftChild); pre_order_traversal(root->rightChild); } } void inorder_traversal(struct node* root) { if(root != NULL) { inorder_traversal(root->leftChild); printf("%d ",root->data); inorder_traversal(root->rightChild); } } void post_order_traversal(struct node* root) { if(root != NULL) { post_order_traversal(root->leftChild); post_order_traversal(root->rightChild); printf("%d ", root->data); } } int main() {
- 222. Data Structures & Algorithms 213 int i; int array[7] = { 27, 14, 35, 10, 19, 31, 42 }; for(i = 0; i < 7; i++) insert(array[i]); i = 31; struct node * temp = search(i); if(temp != NULL) { printf("[%d] Element found.", temp->data); printf("n"); }else { printf("[ x ] Element not found (%d).n", i); } i = 15; temp = search(i); if(temp != NULL) { printf("[%d] Element found.", temp->data); printf("n"); }else { printf("[ x ] Element not found (%d).n", i); } printf("nPreorder traversal: "); pre_order_traversal(root); printf("nInorder traversal: "); inorder_traversal(root); printf("nPost order traversal: "); post_order_traversal(root); return 0; }
- 223. Data Structures & Algorithms 214 If we compile and run the above program, it will produce the following result − Visiting elements: 27 35 [31] Element found. Visiting elements: 27 14 19 [ x ] Element not found (15). Preorder traversal: 27 14 10 19 35 31 42 Inorder traversal: 10 14 19 27 31 35 42 Post order traversal: 10 19 14 31 42 35 27
- 224. Data Structures & Algorithms 215 A Binary Search Tree (BST) is a tree in which all the nodes follow the below-mentioned properties − The left sub-tree of a node has a key less than or equal to its parent node's key. The right sub-tree of a node has a key greater than or equal to its parent node's key. Thus, BST divides all its sub-trees into two segments; the left sub-tree and the right sub- tree and can be defined as − left_subtree (keys) ≤ node (key) ≤ right_subtree (keys) Representation BST is a collection of nodes arranged in a way where they maintain BST properties. Each node has a key and an associated value. While searching, the desired key is compared to the keys in BST and if found, the associated value is retrieved. Following is a pictorial representation of BST − We observe that the root node key (27) has all less-valued keys on the left sub-tree and the higher valued keys on the right sub-tree. 32. Binary Search Tree
- 225. Data Structures & Algorithms 216 BasicOperations Following are the basic operations of a tree - Search − Searches an element in a tree. Insert − Inserts an element in a tree. Pre-order Traversal − Traverses a tree in a pre-order manner. In-order Traversal − Traverses a tree in an in-order manner. Post-order Traversal − Traverses a tree in a post-order manner. Node Define a node having some data, references to its left and right child nodes. struct node { int data; struct node *leftChild; struct node *rightChild; }; SearchOperation Whenever an element is to be searched, start searching from the root node. Then if the data is less than the key value, search for the element in the left subtree. Otherwise, search for the element in the right subtree. Follow the same algorithm for each node. struct node* search(int data){ struct node *current = root; printf("Visiting elements: "); while(current->data != data){ if(current != NULL) { printf("%d ",current->data); //go to left tree if(current->data > data){ current = current->leftChild;
- 226. Data Structures & Algorithms 217 }//else go to right tree else { current = current->rightChild; } //not found if(current == NULL){ return NULL; } } } return current; } InsertOperation Whenever an element is to be inserted, first locate its proper location. Start searching from the root node, then if the data is less than the key value, search for the empty location in the left subtree and insert the data. Otherwise, search for the empty location in the right subtree and insert the data. void insert(int data){ struct node *tempNode = (struct node*) malloc(sizeof(struct node)); struct node *current; struct node *parent; tempNode->data = data; tempNode->leftChild = NULL; tempNode->rightChild = NULL; //if tree is empty if(root == NULL){ root = tempNode; }else { current = root; parent = NULL; while(1){ parent = current;
- 227. Data Structures & Algorithms 218 //go to left of the tree if(data < parent->data){ current = current->leftChild; //insert to the left if(current == NULL){ parent->leftChild = tempNode; return; } }//go to right of the tree else{ current = current->rightChild; //insert to the right if(current == NULL){ parent->rightChild = tempNode; return; } } } } }
- 228. Data Structures & Algorithms 219 What if the input to binary search tree comes in a sorted (ascending or descending) manner? It will then look like this − It is observed that BST's worst-case performance is closest to linear search algorithms, that is Ο(n). In real-time data, we cannot predict data pattern and their frequencies. So, a need arises to balance out the existing BST. Named after their inventor Adelson, Velski & Landis, AVL trees are height balancing binary search tree. AVL tree checks the height of the left and the right sub-trees and assures that the difference is not more than 1. This difference is called the Balance Factor. Here we see that the first tree is balanced and the next two trees are not balanced − 33. AVL Trees
- 229. Data Structures & Algorithms 220 In the second tree, the left subtree of C has height 2 and the right subtree has height 0, so the difference is 2. In the third tree, the right subtree of A has height 2 and the left is missing, so it is 0, and the difference is 2 again. AVL tree permits difference (balance factor) to be only 1. BalanceFactor = height(left-sutree) − height(right-sutree) If the difference in the height of left and right sub-trees is more than 1, the tree is balanced using some rotation techniques. AVLRotations To balance itself, an AVL tree may perform the following four kinds of rotations − Left rotation Right rotation Left-Right rotation Right-Left rotation The first two rotations are single rotations and the next two rotations are double rotations. To have an unbalanced tree, we at least need a tree of height 2. With this simple tree, let's understand them one by one. Left Rotation If a tree becomes unbalanced, when a node is inserted into the right subtree of the right subtree, then we perform a single left rotation − In our example, node A has become unbalanced as a node is inserted in the right subtree of A's right subtree. We perform the left rotation by making A the left-subtree of B.
- 230. Data Structures & Algorithms 221 Right Rotation AVL tree may become unbalanced, if a node is inserted in the left subtree of the left subtree. The tree then needs a right rotation. As depicted, the unbalanced node becomes the right child of its left child by performing a right rotation. Left-Right Rotation Double rotations are slightly complex version of already explained versions of rotations. To understand them better, we should take note of each action performed while rotation. Let's first check how to perform Left-Right rotation. A left-right rotation is a combination of left rotation followed by right rotation. State Action A node has been inserted into the right subtree of the left subtree. This makes C an unbalanced node. These scenarios cause AVL tree to perform left-right rotation. We first perform the left rotation on the left subtree of C. This makes A, the left subtree of B.
- 231. Data Structures & Algorithms 222 Node C is still unbalanced, however now, it is because of the left-subtree of the left-subtree. We shall now right-rotate the tree, making B the new root node of this subtree. C now becomes the right subtree of its own left subtree. The tree is now balanced. Right-Left Rotation The second type of double rotation is Right-Left Rotation. It is a combination of right rotation followed by left rotation. State Action A node has been inserted into the left subtree of the right subtree. This makes A, an unbalanced node with balance factor 2.
- 232. Data Structures & Algorithms 223 First, we perform the right rotation along C node, making C the right subtree of its own left subtree B. Now, B becomes the right subtree of A. Node A is still unbalanced because of the right subtree of its right subtree and requires a left rotation. A left rotation is performed by making B the new root node of the subtree. A becomes the left subtree of its right subtree B. The tree is now balanced.
- 233. Data Structures & Algorithms 224 A spanning tree is a subset of Graph G, which has all the vertices covered with minimum possible number of edges. Hence, a spanning tree does not have cycles and it cannot be disconnected. By this definition, we can draw a conclusion that every connected and undirected Graph G has at least one spanning tree. A disconnected graph does not have any spanning tree, as it cannot be spanned to all its vertices. We found three spanning trees off one complete graph. A complete undirected graph can have maximum nn-2 number of spanning trees, where n is the number of nodes. In the above addressed example, n is 3, hence 33−2 = 3 spanning trees are possible. GeneralPropertiesofSpanningTree We now understand that one graph can have more than one spanning tree. Following are a few properties of the spanning tree connected to graph G - A connected graph G can have more than one spanning tree. All possible spanning trees of graph G, have the same number of edges and vertices. The spanning tree does not have any cycle (loops). 34. Spanning Tree
- 234. Data Structures & Algorithms 225 Removing one edge from the spanning tree will make the graph disconnected, i.e. the spanning tree is minimally connected. Adding one edge to the spanning tree will create a circuit or loop, i.e. the spanning tree is maximally acyclic. MathematicalPropertiesofSpanningTree Spanning tree has n-1 edges, where n is the number of nodes (vertices). From a complete graph, by removing maximum e-n+1 edges, we can construct a spanning tree. A complete graph can have maximum nn-2 number of spanning trees. Thus, we can conclude that spanning trees are a subset of connected Graph G and disconnected graphs do not have spanning tree. ApplicationofSpanningTree Spanning tree is basically used to find a minimum path to connect all nodes in a graph. Common application of spanning trees are − Civil Network Planning Computer Network Routing Protocol Cluster Analysis Let us understand this through a small example. Consider, city network as a huge graph and now plans to deploy telephone lines in such a way that in minimum lines we can connect to all city nodes. This is where the spanning tree comes into picture. MinimumSpanningTree(MST) In a weighted graph, a minimum spanning tree is a spanning tree that has minimum weight than all other spanning trees of the same graph. In real-world situations, this weight can be measured as distance, congestion, traffic load or any arbitrary value denoted to the edges. MinimumSpanning-TreeAlgorithm We shall learn about two most important spanning tree algorithms here − Kruskal's Algorithm Prim's Algorithm Both are greedy algorithms.
- 235. Data Structures & Algorithms 226 Kruskal'sSpanningTreeAlgorithm Kruskal's algorithm to find the minimum cost spanning tree uses the greedy approach. This algorithm treats the graph as a forest and every node it has as an individual tree. A tree connects to another only and only if, it has the least cost among all available options and does not violate MST properties. To understand Kruskal's algorithm let us consider the following example − Step 1 - Remove all loops and parallel edges Remove all loops and parallel edges from the given graph.
- 236. Data Structures & Algorithms 227 In case of parallel edges, keep the one which has the least cost associated and remove all others. Step 2 - Arrange all edges in their increasing order of weight The next step is to create a set of edges and weight, and arrange them in an ascending order of weightage (cost). Step 3 - Add the edge which has the least weightage Now we start adding edges to the graph beginning from the one which has the least weight. Throughout, we shall keep checking that the spanning properties remain intact. In case, by adding one edge, the spanning tree property does not hold then we shall consider not to include the edge in the graph.
- 237. Data Structures & Algorithms 228 The least cost is 2 and edges involved are B,D and D,T. We add them. Adding them does not violate spanning tree properties, so we continue to our next edge selection. Next cost is 3, and associated edges are A,C and C,D. We add them again − Next cost in the table is 4, and we observe that adding it will create a circuit in the graph. We ignore it. In the process we shall ignore/avoid all edges that create a circuit.
- 238. Data Structures & Algorithms 229 We observe that edges with cost 5 and 6 also create circuits. We ignore them and move on. Now we are left with only one node to be added. Between the two least cost edges available 7 and 8, we shall add the edge with cost 7. By adding edge S,A we have included all the nodes of the graph and we now have minimum cost spanning tree. Prim'sSpanningTreeAlgorithm Prim's algorithm to find minimum cost spanning tree (as Kruskal's algorithm) uses the greedy approach. Prim's algorithm shares a similarity with the shortest path first algorithms. Prim's algorithm, in contrast with Kruskal's algorithm, treats the nodes as a single tree and keeps on adding new nodes to the spanning tree from the given graph.
- 239. Data Structures & Algorithms 230 To contrast with Kruskal's algorithm and to understand Prim's algorithm better, we shall use the same example − Step 1 - Remove all loops and parallel edges
- 240. Data Structures & Algorithms 231 Remove all loops and parallel edges from the given graph. In case of parallel edges, keep the one which has the least cost associated and remove all others. Step 2 - Choose any arbitrary node as root node In this case, we choose S node as the root node of Prim's spanning tree. This node is arbitrarily chosen, so any node can be the root node. One may wonder why any video can be a root node. So the answer is, in the spanning tree all the nodes of a graph are included and because it is connected then there must be at least one edge, which will join it to the rest of the tree. Step 3 - Check outgoing edges and select the one with less cost After choosing the root node S, we see that S,A and S,C are two edges with weight 7 and 8, respectively. We choose the edge S,A as it is lesser than the other.
- 241. Data Structures & Algorithms 232 Now, the tree S-7-A is treated as one node and we check for all edges going out from it. We select the one which has the lowest cost and include it in the tree. After this step, S-7-A-3-C tree is formed. Now we'll again treat it as a node and will check all the edges again. However, we will choose only the least cost edge. In this case, C-3-D is the new edge, which is less than other edges' cost 8, 6, 4, etc. After adding node D to the spanning tree, we now have two edges going out of it having the same cost, i.e. D-2-T and D-2-B. Thus, we can add either one. But the next step will again yield edge 2 as the least cost. Hence, we are showing a spanning tree with both edges included. We may find that the output spanning tree of the same graph using two different algorithms is same.
- 242. Data Structures & Algorithms 233 Heap is a special case of balanced binary tree data structure where the root-node key is compared with its children and arranged accordingly. If α has child node β then − key(α) ≥ key(β) As the value of parent is greater than that of child, this property generates Max Heap. Based on this criteria, a heap can be of two types − For Input → 35 33 42 10 14 19 27 44 26 31 Min-Heap − Where the value of the root node is less than or equal to either of its children. Max-Heap − Where the value of the root node is greater than or equal to either of its children. 35. Heaps
- 243. Data Structures & Algorithms 234 Both trees are constructed using the same input and order of arrival. MaxHeapConstructionAlgorithm We shall use the same example to demonstrate how a Max Heap is created. The procedure to create Min Heap is similar but we go for min values instead of max values. We are going to derive an algorithm for max heap by inserting one element at a time. At any point of time, heap must maintain its property. While insertion, we also assume that we are inserting a node in an already heapified tree. Step 1 − Create a new node at the end of heap. Step 2 − Assign new value to the node. Step 3 − Compare the value of this child node with its parent. Step 4 − If value of parent is less than child, then swap them. Step 5 − Repeat step 3 & 4 until Heap property holds. Note − In Min Heap construction algorithm, we expect the value of the parent node to be less than that of the child node. Let's understand Max Heap construction by an animated illustration. We consider the same input sample that we used earlier.
- 244. Data Structures & Algorithms 235 MaxHeapDeletionAlgorithm Let us derive an algorithm to delete from max heap. Deletion in Max (or Min) Heap always happens at the root to remove the Maximum (or minimum) value. Step 1 − Remove root node. Step 2 − Move the last element of last level to root. Step 3 − Compare the value of this child node with its parent. Step 4 − If value of parent is less than child, then swap them. Step 5 − Repeat step 3 & 4 until Heap property holds.
- 245. Data Structures & Algorithms 236 Recursion
- 246. Data Structures & Algorithms 237 Some computer programming languages allow a module or function to call itself. This technique is known as recursion. In recursion, a function α either calls itself directly or calls a function β that in turn calls the original function α. The function α is called recursive function. Example − a function calling itself. int function(int value) { if(value < 1) return; function(value - 1); printf("%d ",value); } Example − a function that calls another function which in turn calls it again. int function(int value) { if(value < 1) return; function(value - 1); printf("%d ",value); } Properties A recursive function can go infinite like a loop. To avoid infinite running of recursive function, there are two properties that a recursive function must have − Base criteria − There must be at least one base criteria or condition, such that, when this condition is met the function stops calling itself recursively. Progressive approach − The recursive calls should progress in such a way that each time a recursive call is made it comes closer to the base criteria. 36. Recursion ─ Basics
- 247. Data Structures & Algorithms 238 Implementation Many programming languages implement recursion by means of stacks. Generally, whenever a function (caller) calls another function (callee) or itself as callee, the caller function transfers execution control to the callee. This transfer process may also involve some data to be passed from the caller to the callee. This implies, the caller function has to suspend its execution temporarily and resume later when the execution control returns from the callee function. Here, the caller function needs to start exactly from the point of execution where it puts itself on hold. It also needs the exact same data values it was working on. For this purpose, an activation record (or stack frame) is created for the caller function. This activation record keeps the information about local variables, formal parameters, return address and all information passed to the caller function. AnalysisofRecursion One may argue why to use recursion, as the same task can be done with iteration. The first reason is, recursion makes a program more readable and because of latest enhanced CPU systems, recursion is more efficient than iterations. TimeComplexity In case of iterations, we take number of iterations to count the time complexity. Likewise, in case of recursion, assuming everything is constant, we try to figure out the number of times a recursive call is being made. A call made to a function is Ο(1), hence the (n) number of times a recursive call is made makes the recursive function Ο(n).
- 248. Data Structures & Algorithms 239 SpaceComplexity Space complexity is counted as what amount of extra space is required for a module to execute. In case of iterations, the compiler hardly requires any extra space. The compiler keeps updating the values of variables used in the iterations. But in case of recursion, the system needs to store activation record each time a recursive call is made. Hence, it is considered that space complexity of recursive function may go higher than that of a function with iteration.
- 249. Data Structures & Algorithms 240 Tower of Hanoi, is a mathematical puzzle which consists of three towers (pegs) and more than one rings is as depicted − These rings are of different sizes and stacked upon in an ascending order, i.e. the smaller one sits over the larger one. There are other variations of the puzzle where the number of disks increase, but the tower count remains the same. Rules The mission is to move all the disks to some another tower without violating the sequence of arrangement. A few rules to be followed for Tower of Hanoi are − Only one disk can be moved among the towers at any given time. Only the "top" disk can be removed. No large disk can sit over a small disk. 37. Tower of Hanoi
- 250. Data Structures & Algorithms 241 Following is an animated representation of solving a Tower of Hanoi puzzle with three disks.
- 251. Data Structures & Algorithms 242
- 252. Data Structures & Algorithms 243 Tower of Hanoi puzzle with n disks can be solved in minimum 2n −1 steps. This presentation shows that a puzzle with 3 disks has taken 23 −1 = 7 steps.
- 253. Data Structures & Algorithms 244 Algorithm To write an algorithm for Tower of Hanoi, first we need to learn how to solve this problem with lesser amount of disks, say → 1 or 2. We mark three towers with name, source, destination and aux (only to help moving the disks). If we have only one disk, then it can easily be moved from source to destination peg. If we have 2 disks – First, we move the smaller (top) disk to aux peg. Then, we move the larger (bottom) disk to destination peg. And finally, we move the smaller disk from aux to destination peg.
- 254. Data Structures & Algorithms 245
- 255. Data Structures & Algorithms 246 So now, we are in a position to design an algorithm for Tower of Hanoi with more than two disks. We divide the stack of disks in two parts. The largest disk (nth disk) is in one part and all other (n-1) disks are in the second part. Our ultimate aim is to move disk n from source to destination and then put all other (n- 1) disks onto it. We can imagine to apply the same in a recursive way for all given set of disks. The steps to follow are − Step 1 − Move n-1 disks from source to aux Step 2 − Move nth disk from source to dest Step 3 − Move n-1 disks from aux to dest A recursive algorithm for Tower of Hanoi can be driven as follows − START Procedure Hanoi(disk, source, dest, aux) IF disk == 0, THEN move disk from source to dest ELSE Hanoi(disk - 1, source, aux, dest) // Step 1 move disk from source to dest // Step 2 Hanoi(disk - 1, aux, dest, source) // Step 3 END IF END Procedure STOP To check the implementation in C programming, click here.
- 256. Data Structures & Algorithms 247 TowerofHanoiinC Program #include <stdio.h> #include <stdbool.h> #define MAX 10 int list[MAX] = {1,8,4,6,0,3,5,2,7,9}; void display(){ int i; printf("["); // navigate through all items for(i = 0; i < MAX; i++){ printf("%d ",list[i]); } printf("]n"); } void bubbleSort() { int temp; int i,j; bool swapped = false; // loop through all numbers for(i = 0; i < MAX-1; i++) { swapped = false; // loop through numbers falling ahead for(j = 0; j < MAX-1-i; j++) { printf("Items compared: [ %d, %d ] ", list[j],list[j+1]);
- 257. Data Structures & Algorithms 248 // check if next number is lesser than current no // swap the numbers. // (Bubble up the highest number) if(list[j] > list[j+1]) { temp = list[j]; list[j] = list[j+1]; list[j+1] = temp; swapped = true; printf(" => swapped [%d, %d]n",list[j],list[j+1]); }else { printf(" => not swappedn"); } } // if no number was swapped that means // array is sorted now, break the loop. if(!swapped) { break; } printf("Iteration %d#: ",(i+1)); display(); } } main(){ printf("Input Array: "); display(); printf("n"); bubbleSort(); printf("nOutput Array: "); display(); }
- 258. Data Structures & Algorithms 249 If we compile and run the above program, it will produce the following result − Input Array: [1 8 4 6 0 3 5 2 7 9 ] Items compared: [ 1, 8 ] => not swapped Items compared: [ 8, 4 ] => swapped [4, 8] Items compared: [ 8, 6 ] => swapped [6, 8] Items compared: [ 8, 0 ] => swapped [0, 8] Items compared: [ 8, 3 ] => swapped [3, 8] Items compared: [ 8, 5 ] => swapped [5, 8] Items compared: [ 8, 2 ] => swapped [2, 8] Items compared: [ 8, 7 ] => swapped [7, 8] Items compared: [ 8, 9 ] => not swapped Iteration 1#: [1 4 6 0 3 5 2 7 8 9 ] Items compared: [ 1, 4 ] => not swapped Items compared: [ 4, 6 ] => not swapped Items compared: [ 6, 0 ] => swapped [0, 6] Items compared: [ 6, 3 ] => swapped [3, 6] Items compared: [ 6, 5 ] => swapped [5, 6] Items compared: [ 6, 2 ] => swapped [2, 6] Items compared: [ 6, 7 ] => not swapped Items compared: [ 7, 8 ] => not swapped Iteration 2#: [1 4 0 3 5 2 6 7 8 9 ] Items compared: [ 1, 4 ] => not swapped Items compared: [ 4, 0 ] => swapped [0, 4] Items compared: [ 4, 3 ] => swapped [3, 4] Items compared: [ 4, 5 ] => not swapped Items compared: [ 5, 2 ] => swapped [2, 5] Items compared: [ 5, 6 ] => not swapped Items compared: [ 6, 7 ] => not swapped Iteration 3#: [1 0 3 4 2 5 6 7 8 9 ] Items compared: [ 1, 0 ] => swapped [0, 1] Items compared: [ 1, 3 ] => not swapped Items compared: [ 3, 4 ] => not swapped Items compared: [ 4, 2 ] => swapped [2, 4] Items compared: [ 4, 5 ] => not swapped Items compared: [ 5, 6 ] => not swapped
- 259. Data Structures & Algorithms 250 Iteration 4#: [0 1 3 2 4 5 6 7 8 9 ] Items compared: [ 0, 1 ] => not swapped Items compared: [ 1, 3 ] => not swapped Items compared: [ 3, 2 ] => swapped [2, 3] Items compared: [ 3, 4 ] => not swapped Items compared: [ 4, 5 ] => not swapped Iteration 5#: [0 1 2 3 4 5 6 7 8 9 ] Items compared: [ 0, 1 ] => not swapped Items compared: [ 1, 2 ] => not swapped Items compared: [ 2, 3 ] => not swapped Items compared: [ 3, 4 ] => not swapped Output Array: [0 1 2 3 4 5 6 7 8 9 ]
- 260. Data Structures & Algorithms 251 Fibonacci series generates the subsequent number by adding two previous numbers. Fibonacci series starts from two numbers − F0 & F1. The initial values of F0 & F1 can be taken as 0, 1 or 1, 1 respectively. Fibonacci series satisfies the following conditions − Fn = Fn-1 + Fn-2 Hence, a Fibonacci series can look like this − F8 = 0 1 1 2 3 5 8 13 or, this − F8 = 1 1 2 3 5 8 13 21 For illustration purpose, Fibonacci of F8 is displayed as − 38. Fibonacci Series
- 261. Data Structures & Algorithms 252 FibonacciIterativeAlgorithm First we try to draft the iterative algorithm for Fibonacci series. Procedure Fibonacci(n) declare f0, f1, fib, loop set f0 to 0 set f1 to 1 display f0, f1 for loop ← 1 to n fib ← f0 + f1 f0 ← f1 f1 ← fib display fib end for end procedure To know about the implementation of the above algorithm in C programming language, click here. FibonacciInteractivePrograminC Fibonacci Program in C RecursionDemo.c #include <stdio.h> int factorial(int n){ //base case if(n == 0){ return 1;
- 262. Data Structures & Algorithms 253 }else { return n * factorial(n-1); } } int fibbonacci(int n){ if(n == 0){ return 0; }else if(n == 1){ return 1; }else { return (fibbonacci(n-1) + fibbonacci(n-2)); } } main(){ int n = 5; int i; printf("Factorial of %d: %dn" , n , factorial(n)); printf("Fibbonacci of %d: " , n); for(i = 0;i<n;i++){ printf("%d ",fibbonacci(i)); } } If we compile and run the above program, it will produce the following result − Factorial of 5: 120 Fibbonacci of 5: 0 1 1 2 3
- 263. Data Structures & Algorithms 254 FibonacciRecursiveAlgorithm Let us learn how to create a recursive algorithm Fibonacci series. The base criteria of recursion. START Procedure Fibonacci(n) declare f0, f1, fib, loop set f0 to 0 set f1 to 1 display f0, f1 for loop ← 1 to n fib ← f0 + f1 f0 ← f1 f1 ← fib display fib end for END To know about the implementation of the above algorithm in C programming language, click here. FibonacciRecursivePrograminC Fibonacci Program in C #include <stdio.h> int factorial(int n){ //base case if(n == 0){ return 1;
- 264. Data Structures & Algorithms 255 }else { return n * factorial(n-1); } } int fibbonacci(int n){ if(n == 0){ return 0; }else if(n == 1){ return 1; }else { return (fibbonacci(n-1) + fibbonacci(n-2)); } } main(){ int n = 5; int i; printf("Factorial of %d: %dn" , n , factorial(n)); printf("Fibbonacci of %d: " , n); for(i = 0;i<n;i++){ printf("%d ",fibbonacci(i)); } } If we compile and run the above program, it will produce the following result − Factorial of 5: 120 Fibbonacci of 5: 0 1 1 2 3






















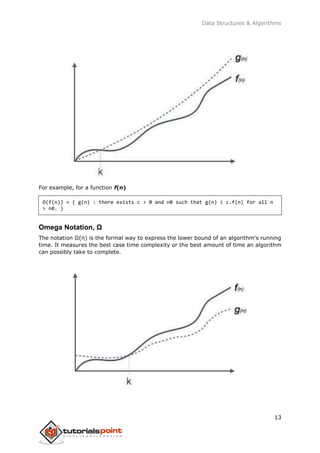
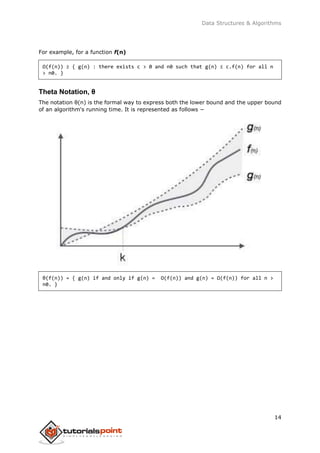











![Data Structures & Algorithms
26
Example
Result
Let LA be a Linear Array (unordered) with N elements and K is a positive integer such
that K<=N. Following is the algorithm where ITEM is inserted into the Kth
position of LA −
1. Start
2. Set J=N
3. Set N = N+1
4. Repeat steps 5 and 6 while J >= K
5. Set LA[J+1] = LA[J]
6. Set J = J-1
7. Set LA[K] = ITEM
8. Stop
Example
Following is the implementation of the above algorithm −
#include <stdio.h>
main() {
int LA[] = {1,3,5,7,8};
int item = 10, k = 3, n = 5;
int i = 0, j = n;
printf("The original array elements are :n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d n", i, LA[i]);
}
n = n + 1;
while( j >= k){
LA[j+1] = LA[j];
j = j - 1;
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-35-320.jpg)
![Data Structures & Algorithms
27
LA[k] = item;
printf("The array elements after insertion :n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d n", i, LA[i]);
}
}
When we compile and execute the above program, it produces the following result −
The original array elements are :
LA[0]=1
LA[1]=3
LA[2]=5
LA[3]=7
LA[4]=8
The array elements after insertion :
LA[0]=1
LA[1]=3
LA[2]=5
LA[3]=10
LA[4]=7
LA[5]=8
For other variations of array insertion operation click here
ArrayInsertions
In the previous section, we have learnt how the insertion operation works. It is not always
necessary that an element is inserted at the end of an array. Following can be a situation
with array insertion −
Insertion at the beginning of an array
Insertion at the given index of an array
Insertion after the given index of an array
Insertion before the given index of an array](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-36-320.jpg)
![Data Structures & Algorithms
28
InsertionattheBeginningofanArray
When the insertion happens at the beginning, it causes all the existing data items to shift
one step downward. Here, we design and implement an algorithm to insert an element at
the beginning of an array.
Algorithm
We assume A is an array with N elements. The maximum numbers of elements it can
store is defined by MAX. We shall first check if an array has any empty space to store any
element and then we proceed with the insertion process.
begin
IF N = MAX, return
ELSE
N = N + 1
For All Elements in A
Move to next adjacent location
A[FIRST] = New_Element
end
Implementation in C
#include <stdio.h>
#define MAX 5
void main() {
int array[MAX] = {2, 3, 4, 5};
int N = 4; // number of elements in array
int i = 0; // loop variable
int value = 1; // new data element to be stored in array
// print array before insertion
printf("Printing array before insertion −n");](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-37-320.jpg)
![Data Structures & Algorithms
29
for(i = 0; i < N; i++) {
printf("array[%d] = %d n", i, array[i]);
}
// now shift rest of the elements downwards
for(i = N; i >= 0; i--) {
array[i+1] = array[i];
}
// add new element at first position
array[0] = value;
// increase N to reflect number of elements
N++;
// print to confirm
printf("Printing array after insertion −n");
for(i = 0; i < N; i++) {
printf("array[%d] = %dn", i, array[i]);
}
}
This program should yield the following output −
Printing array before insertion −
array[0] = 2
array[1] = 3
array[2] = 4
array[3] = 5
Printing array after insertion −
array[0] = 0
array[1] = 2
array[2] = 3
array[3] = 4
array[4] = 5](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-38-320.jpg)
![Data Structures & Algorithms
30
InsertionattheGivenIndexofanArray
In this scenario, we are given the exact location (index) of an array where a new data
element (value) needs to be inserted. First we shall check if the array is full, if it is not,
then we shall move all data elements from that location one step downward. This will make
room for a new data element.
Algorithm
We assume A is an array with N elements. The maximum numbers of elements it can
store is defined by MAX.
begin
IF N = MAX, return
ELSE
N = N + 1
SEEK Location index
For All Elements from A[index] to A[N]
Move to next adjacent location
A[index] = New_Element
end
Implementation in C
#include <stdio.h>
#define MAX 5
void main() {
int array[MAX] = {1, 2, 4, 5};
int N = 4; // number of elements in array
int i = 0; // loop variable
int index = 2; // index location to insert new value
int value = 3; // new data element to be inserted
// print array before insertion
printf("Printing array before insertion −n");](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-39-320.jpg)
![Data Structures & Algorithms
31
for(i = 0; i < N; i++) {
printf("array[%d] = %d n", i, array[i]);
}
// now shift rest of the elements downwards
for(i = N; i >= index; i--) {
array[i+1] = array[i];
}
// add new element at first position
array[index] = value;
// increase N to reflect number of elements
N++;
// print to confirm
printf("Printing array after insertion −n");
for(i = 0; i < N; i++) {
printf("array[%d] = %dn", i, array[i]);
}
}
If we compile and run the above program, it will produce the following result −
Printing array before insertion −
array[0] = 1
array[1] = 2
array[2] = 4
array[3] = 5
Printing array after insertion −
array[0] = 1
array[1] = 2
array[2] = 3
array[3] = 4
array[4] = 5](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-40-320.jpg)
![Data Structures & Algorithms
32
InsertionAftertheGivenIndexofanArray
In this scenario we are given a location (index) of an array after which a new data element
(value) has to be inserted. Only the seek process varies, the rest of the activities are the
same as in the previous example.
Algorithm
We assume A is an array with N elements. The maximum numbers of elements it can
store is defined by MAX.
begin
IF N = MAX, return
ELSE
N = N + 1
SEEK Location index
For All Elements from A[index + 1] to A[N]
Move to next adjacent location
A[index + 1] = New_Element
end
Implementation in C
#include <stdio.h>
#define MAX 5
void main() {
int array[MAX] = {1, 2, 4, 5};
int N = 4; // number of elements in array
int i = 0; // loop variable
int index = 1; // index location after which value will be inserted
int value = 3; // new data element to be inserted
// print array before insertion
printf("Printing array before insertion −n");](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-41-320.jpg)
![Data Structures & Algorithms
33
for(i = 0; i < N; i++) {
printf("array[%d] = %d n", i, array[i]);
}
// now shift rest of the elements downwards
for(i = N; i >= index + 1; i--) {
array[i + 1] = array[i];
}
// add new element at first position
array[index + 1] = value;
// increase N to reflect number of elements
N++;
// print to confirm
printf("Printing array after insertion −n");
for(i = 0; i < N; i++) {
printf("array[%d] = %dn", i, array[i]);
}
}
If we compile and run the above program, it will produce the following result −
Printing array before insertion −
array[0] = 1
array[1] = 2
array[2] = 4
array[3] = 5
Printing array after insertion −
array[0] = 1
array[1] = 2
array[2] = 3
array[3] = 4](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-42-320.jpg)
![Data Structures & Algorithms
34
array[4] = 5
InsertionBeforetheGivenIndexofanArray
In this scenario we are given a location (index) of an array before which a new data
element (value) has to be inserted. This time we seek till index-1, i.e., one location
ahead of the given index. Rest of the activities are the same as in the previous example.
Algorithm
We assume A is an array with N elements. The maximum numbers of elements it can
store is defined by MAX.
begin
IF N = MAX, return
ELSE
N = N + 1
SEEK Location index
For All Elements from A[index - 1] to A[N]
Move to next adjacent location
A[index - 1] = New_Element
end
Implementation in C
#include <stdio.h>
#define MAX 5](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-43-320.jpg)
![Data Structures & Algorithms
35
void main() {
int array[MAX] = {1, 2, 4, 5};
int N = 4; // number of elements in array
int i = 0; // loop variable
int index = 3; // index location before which value will be inserted
int value = 3; // new data element to be inserted
// print array before insertion
printf("Printing array before insertion −n");
for(i = 0; i < N; i++) {
printf("array[%d] = %d n", i, array[i]);
}
// now shift rest of the elements downwards
for(i = N; i >= index + 1; i--) {
array[i + 1] = array[i];
}
// add new element at first position
array[index + 1] = value;
// increase N to reflect number of elements
N++;
// print to confirm
printf("Printing array after insertion −n");
for(i = 0; i < N; i++) {
printf("array[%d] = %dn", i, array[i]);
}
}
If we compile and run the above program, it will produce the following result −
Printing array before insertion −
array[0] = 1
array[1] = 2](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-44-320.jpg)
![Data Structures & Algorithms
36
array[2] = 4
array[3] = 5
Printing array after insertion −
array[0] = 1
array[1] = 2
array[2] = 4
array[3] = 5
array[4] = 3
DeletionOperation
Deletion refers to removing an existing element from the array and re-organizing all
elements of an array.
Algorithm
Consider LA is a linear array with N elements and K is a positive integer such that K<=N.
Following is the algorithm to delete an element available at the Kth
position of LA.
1. Start
2. Set J=K
3. Repeat steps 4 and 5 while J < N
4. Set LA[J-1] = LA[J]
5. Set J = J+1
6. Set N = N-1
7. Stop
Example
Following is the implementation of the above algorithm −
#include <stdio.h>
main() {
int LA[] = {1,3,5,7,8};
int k = 3, n = 5;
int i, j;
printf("The original array elements are :n");](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-45-320.jpg)
![Data Structures & Algorithms
37
for(i = 0; i<n; i++) {
printf("LA[%d] = %d n", i, LA[i]);
}
j = k;
while( j < n){
LA[j-1] = LA[j];
j = j + 1;
}
n = n -1;
printf("The array elements after deletion :n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d n", i, LA[i]);
}
}
When we compile and execute the above program, it produces the following result −
The original array elements are :
LA[0]=1
LA[1]=3
LA[2]=5
LA[3]=7
LA[4]=8
The array elements after deletion :
LA[0]=1
LA[1]=3
LA[2]=7
LA[3]=8
SearchOperation
You can perform a search for an array element based on its value or its index.
Algorithm](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-46-320.jpg)
![Data Structures & Algorithms
38
Consider LA is a linear array with N elements and K is a positive integer such that K<=N.
Following is the algorithm to find an element with a value of ITEM using sequential search.
1. Start
2. Set J=0
3. Repeat steps 4 and 5 while J < N
4. IF LA[J] is equal ITEM THEN GOTO STEP 6
5. Set J = J +1
6. PRINT J, ITEM
7. Stop
Example
Following is the implementation of the above algorithm −
#include <stdio.h>
main() {
int LA[] = {1,3,5,7,8};
int item = 5, n = 5;
int i = 0, j = 0;
printf("The original array elements are :n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d n", i, LA[i]);
}
while( j < n){
if( LA[j] == item ){
break;
}
j = j + 1;
}
printf("Found element %d at position %dn", item, j+1);
}
When we compile and execute the above program, it produces the following result −](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-47-320.jpg)
![Data Structures & Algorithms
39
The original array elements are :
LA[0]=1
LA[1]=3
LA[2]=5
LA[3]=7
LA[4]=8
Found element 5 at position 3
UpdateOperation
Update operation refers to updating an existing element from the array at a given index.
Algorithm
Consider LA is a linear array with N elements and K is a positive integer such that K<=N.
Following is the algorithm to update an element available at the Kth
position of LA.
1. Start
2. Set LA[K-1] = ITEM
3. Stop
Example
Following is the implementation of the above algorithm −
#include <stdio.h>
main() {
int LA[] = {1,3,5,7,8};
int k = 3, n = 5, item = 10;
int i, j;
printf("The original array elements are :n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d n", i, LA[i]);
}
LA[k-1] = item;
printf("The array elements after updation :n");](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-48-320.jpg)
![Data Structures & Algorithms
40
for(i = 0; i<n; i++) {
printf("LA[%d] = %d n", i, LA[i]);
}
}
When we compile and execute the above program, it produces the following result −
The original array elements are :
LA[0]=1
LA[1]=3
LA[2]=5
LA[3]=7
LA[4]=8
The array elements after updation :
LA[0]=1
LA[1]=3
LA[2]=10
LA[3]=7
LA[4]=8](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-49-320.jpg)






![Data Structures & Algorithms
47
Implementation in C
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
struct node
{
int data;
int key;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
//display the list
void printList()
{
struct node *ptr = head;
printf("n[ ");
//start from the beginning
while(ptr != NULL)
{
printf("(%d,%d) ",ptr->key,ptr->data);
ptr = ptr->next;
}
printf(" ]");
}
//insert link at the first location
void insertFirst(int key, int data)
{
//create a link](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-56-320.jpg)






![Data Structures & Algorithms
54
printf("nList after reversing the data: ");
printList();
}
If we compile and run the above program, it will produce the following result −
Original List:
[ (6,56) (5,40) (4,1) (3,30) (2,20) (1,10) ]
Deleted value:(6,56)
Deleted value:(5,40)
Deleted value:(4,1)
Deleted value:(3,30)
Deleted value:(2,20)
Deleted value:(1,10)
List after deleting all items:
[ ]
Restored List:
[ (6,56) (5,40) (4,1) (3,30) (2,20) (1,10) ]
Element found: (4,1)
List after deleting an item:
[ (6,56) (5,40) (3,30) (2,20) (1,10) ]
Element not found.
List after sorting the data:
[ (1,10) (2,20) (3,30) (5,40) (6,56) ]
List after reversing the data:
[ (6,56) (5,40) (3,30) (2,20) (1,10) ]](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-63-320.jpg)





![Data Structures & Algorithms
60
printf(" ]");
}
//display the list from last to first
void displayBackward(){
//start from the last
struct node *ptr = last;
//navigate till the start of the list
printf("n[ ");
while(ptr != NULL){
//print data
printf("(%d,%d) ",ptr->key,ptr->data);
//move to next item
ptr = ptr ->prev;
printf(" ");
}
printf(" ]");
}
//insert link at the first location
void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if(isEmpty()){
//make it the last link
last = link;](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-69-320.jpg)





![Data Structures & Algorithms
66
deleteLast();
displayForward();
printf("nList , insert after key(4) : ");
insertAfter(4,7, 13);
displayForward();
printf("nList , after delete key(4) : ");
delete(4);
displayForward();
}
If we compile and run the above program, it will produce the following result −
List (First to Last):
[ (6,56) (5,40) (4,1) (3,30) (2,20) (1,10) ]
List (Last to first):
[ (1,10) (2,20) (3,30) (4,1) (5,40) (6,56) ]
List , after deleting first record:
[ (5,40) (4,1) (3,30) (2,20) (1,10) ]
List , after deleting last record:
[ (5,40) (4,1) (3,30) (2,20) ]
List , insert after key(4) :
[ (5,40) (4,1) (4,13) (3,30) (2,20) ]
List , after delete key(4) :
[ (5,40) (4,13) (3,30) (2,20) ]](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-75-320.jpg)


![Data Structures & Algorithms
69
//mark next to first link as first
head = head->next;
//return the deleted link
return tempLink;
}
DisplayListOperation
Following code demonstrates the display list operation in a circular linked list.
//display the list
void printList() {
struct node *ptr = head;
printf("n[ ");
//start from the beginning
if(head != NULL) {
while(ptr->next != ptr) {
printf("(%d,%d) ",ptr->key,ptr->data);
ptr = ptr->next;
}
}
printf(" ]");
}
To know about its implementation in C programming language, please click here.
CircularLinkedListPrograminC
Circular Linked List is a variation of Linked list in which the first element points to the last
element and the last element points to the first element. Both Singly Linked List and
Doubly Linked List can be made into a circular linked list.](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-78-320.jpg)


![Data Structures & Algorithms
72
//mark next to first link as first
head = head->next;
//return the deleted link
return tempLink;
}
//display the list
void printList(){
struct node *ptr = head;
printf("n[ ");
//start from the beginning
if(head != NULL){
while(ptr->next != ptr){
printf("(%d,%d) ",ptr->key,ptr->data);
ptr = ptr->next;
}
}
printf(" ]");
}
main() {
insertFirst(1,10);
insertFirst(2,20);
insertFirst(3,30);
insertFirst(4,1);
insertFirst(5,40);
insertFirst(6,56);](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-81-320.jpg)
![Data Structures & Algorithms
73
printf("Original List: ");
//print list
printList();
while(!isEmpty()){
struct node *temp = deleteFirst();
printf("nDeleted value:");
printf("(%d,%d) ",temp->key,temp->data);
}
printf("nList after deleting all items: ");
printList();
}
If we compile and run the above program, it will produce the following result −
Original List:
[ (6,56) (5,40) (4,1) (3,30) (2,20) ]
Deleted value:(6,56)
Deleted value:(5,40)
Deleted value:(4,1)
Deleted value:(3,30)
Deleted value:(2,20)
Deleted value:(1,10)
List after deleting all items:
[ ]](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-82-320.jpg)


![Data Structures & Algorithms
76
BasicOperations
Stack operations may involve initializing the stack, using it and then de-initializing it. Apart
from these basic stuffs, a stack is used for the following two primary operations −
push() − Pushing (storing) an element on the stack.
pop() − Removing (accessing) an element from the stack.
When data is PUSHed onto stack.
To use a stack efficiently, we need to check the status of stack as well. For the same
purpose, the following functionality is added to stacks −
peek() − get the top data element of the stack, without removing it.
isFull() − check if stack is full.
isEmpty() − check if stack is empty.
At all times, we maintain a pointer to the last PUSHed data on the stack. As this pointer
always represents the top of the stack, hence named top. The top pointer provides top
value of the stack without actually removing it.
First we should learn about procedures to support stack functions −
peek()
Algorithm of peek() function −
begin procedure peek
return stack[top]
end procedure
Implementation of peek() function in C programming language −
int peek() {
return stack[top];
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-85-320.jpg)


![Data Structures & Algorithms
79
If the linked list is used to implement the stack, then in step 3, we need to allocate space
dynamically.
Algorithm for PUSH Operation
A simple algorithm for Push operation can be derived as follows −
begin procedure push: stack, data
if stack is full
return null
endif
top ← top + 1
stack[top] ← data
end procedure
Implementation of this algorithm in C, is very easy. See the following code −
void push(int data) {
if(!isFull()) {
top = top + 1;
stack[top] = data;
}else {
printf("Could not insert data, Stack is full.n");
}
}
PopOperation
Accessing the content while removing it from the stack, is known as a Pop Operation. In
an array implementation of pop() operation, the data element is not actually removed,
instead top is decremented to a lower position in the stack to point to the next value. But
in linked-list implementation, pop() actually removes data element and deallocates
memory space.
A Pop operation may involve the following steps −
Step 1 − Checks if the stack is empty.
Step 2 − If the stack is empty, produces an error and exit.](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-88-320.jpg)
![Data Structures & Algorithms
80
Step 3 − If the stack is not empty, accesses the data element at which top is
pointing.
Step 4 − Decreases the value of top by 1.
Step 5 − Returns success.
Algorithm for Pop Operation
A simple algorithm for Pop operation can be derived as follows −
begin procedure pop: stack
if stack is empty
return null
endif
data ← stack[top]
top ← top - 1
return data
end procedure](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-89-320.jpg)
![Data Structures & Algorithms
81
Implementation of this algorithm in C, is as follows −
int pop(int data) {
if(!isempty()) {
data = stack[top];
top = top - 1;
return data;
}else {
printf("Could not retrieve data, Stack is empty.n");
}
}
For a complete stack program in C programming language, please click here.
StackPrograminC
We shall see the stack implementation in C programming language here. You can try the
program by clicking on the Try-it button. To learn the theory aspect of stacks, click on visit
previous page.
Implementation in C
#include <stdio.h>
int MAXSIZE = 8;
int stack[8];
int top = -1;
int isempty() {
if(top == -1)
return 1;
else
return 0;
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-90-320.jpg)
![Data Structures & Algorithms
82
int isfull() {
if(top == MAXSIZE)
return 1;
else
return 0;
}
int peek() {
return stack[top];
}
int pop() {
int data;
if(!isempty()) {
data = stack[top];
top = top - 1;
return data;
}else {
printf("Could not retrieve data, Stack is empty.n");
}
}
int push(int data) {
if(!isfull()) {
top = top + 1;
stack[top] = data;
}else {
printf("Could not insert data, Stack is full.n");
}
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-91-320.jpg)




![Data Structures & Algorithms
87
In a+b*c, the expression part b*c will be evaluated first, with multiplication as
precedence over addition. We here use parenthesis for a+b to be evaluated first,
like (a+b)*c.
PostfixEvaluationAlgorithm
We shall now look at the algorithm on how to evaluate postfix notation −
Step 1 − scan the expression from left to right
Step 2 − if it is an operand push it to stack
Step 3 − if it is an operator pull operand from stack and perform operation
Step 4 − store the output of step 3, back to stack
Step 5 − scan the expression until all operands are consumed
Step 6 − pop the stack and perform operation
To see the implementation in C programming language, please click here
ExpressionParsingUsingStack
Infix notation is easier for humans to read and understand whereas for electronic machines
like computers, postfix is the best form of expression to parse. We shall see here a program
to convert and evaluate infix notation to postfix notation −
#include<stdio.h>
#include<string.h>
//char stack
char stack[25];
int top = -1;
void push(char item) {
stack[++top] = item;
}
char pop() {
return stack[top--];
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-96-320.jpg)

![Data Structures & Algorithms
89
default:
return 0;
}
}
//converts infix expression to postfix
void convert(char infix[],char postfix[]) {
int i,symbol,j = 0;
stack[++top] = '#';
for(i = 0;i<strlen(infix);i++) {
symbol = infix[i];
if(isOperator(symbol) == 0) {
postfix[j] = symbol;
j++;
} else {
if(symbol == '(') {
push(symbol);
}else {
if(symbol == ')') {
while(stack[top] != '(') {
postfix[j] = pop();
j++;
}
pop();//pop out (.
} else {
if(precedence(symbol)>precedence(stack[top])) {
push(symbol);
}else {
while(precedence(symbol)<=precedence(stack[top])) {
postfix[j] = pop();
j++;
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-98-320.jpg)
![Data Structures & Algorithms
90
push(symbol);
}
}
}
}
}
while(stack[top] != '#') {
postfix[j] = pop();
j++;
}
postfix[j]='0';//null terminate string.
}
//int stack
int stack_int[25];
int top_int = -1;
void push_int(int item) {
stack_int[++top_int] = item;
}
char pop_int() {
return stack_int[top_int--];
}
//evaluates postfix expression
int evaluate(char *postfix){
char ch;
int i = 0,operand1,operand2;
while( (ch = postfix[i++]) != '0') {
if(isdigit(ch)) {](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-99-320.jpg)
![Data Structures & Algorithms
91
push_int(ch-'0'); // Push the operand
}else {
//Operator,pop two operands
operand2 = pop_int();
operand1 = pop_int();
switch(ch) {
case '+':
push_int(operand1+operand2);
break;
case '-':
push_int(operand1-operand2);
break;
case '*':
push_int(operand1*operand2);
break;
case '/':
push_int(operand1/operand2);
break;
}
}
}
return stack_int[top_int];
}
void main() {
char infix[25] = "1*(2+3)",postfix[25];
convert(infix,postfix);
printf("Infix expression is: %sn" , infix);
printf("Postfix expression is: %sn" , postfix);
printf("Evaluated expression is: %dn" , evaluate(postfix));
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-100-320.jpg)


![Data Structures & Algorithms
94
Few more functions are required to make the above-mentioned queue operation efficient.
These are −
peek() − Gets the element at the front of the queue without removing it.
isfull() − Checks if the queue is full.
isempty() − Checks if the queue is empty.
In queue, we always dequeue (or access) data, pointed by front pointer and while
enqueing (or storing) data in the queue we take help of rear pointer.
Let's first learn about supportive functions of a queue −
peek()
This function helps to see the data at the front of the queue. The algorithm of peek()
function is as follows −
begin procedure peek
return queue[front]
end procedure
Implementation of peek() function in C programming language −
int peek() {
return queue[front];
}
isfull()
As we are using single dimension array to implement queue, we just check for the rear
pointer to reach at MAXSIZE to determine that the queue is full. In case we maintain the
queue in a circular linked-list, the algorithm will differ. Algorithm of isfull() function −
begin procedure isfull
if rear equals to MAXSIZE
return true
else](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-103-320.jpg)


![Data Structures & Algorithms
97
Algorithm for enqueue Operation
procedure enqueue(data)
if queue is full
return overflow
endif
rear ← rear + 1
queue[rear] ← data
return true
end procedure
Implementation of enqueue() in C programming language −
int enqueue(int data)
if(isfull())
return 0;
rear = rear + 1;
queue[rear] = data;
return 1;
end procedure
DequeueOperation
Accessing data from the queue is a process of two tasks − access the data where front is
pointing and remove the data after access. The following steps are taken to
perform dequeue operation −
Step 1 − Check if the queue is empty.
Step 2 − If the queue is empty, produce underflow error and exit.
Step 3 − If the queue is not empty, access the data where front is pointing.
Step 4 − Increment front pointer to point to the next available data element.
Step 5 − Return success.](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-106-320.jpg)
![Data Structures & Algorithms
98
Algorithm for dequeue Operation
procedure dequeue
if queue is empty
return underflow
end if
data = queue[front]
front ← front + 1
return true
end procedure
Implementation of dequeue() in C programming language −
int dequeue() {
if(isempty())
return 0;
int data = queue[front];
front = front + 1;
return data;
}
For a complete Queue program in C programming language, please click here.](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-107-320.jpg)
![Data Structures & Algorithms
99
QueuePrograminC
We shall see the stack implementation in C programming language here. You can try the
program by clicking on the Try-it button. To learn the theory aspect of stacks, click on visit
previous page.
Implementation in C
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
return intArray[front];
}
bool isEmpty(){
return itemCount == 0;
}
bool isFull(){
return itemCount == MAX;
}
int size(){
return itemCount;
}
void insert(int data){
if(!isFull()){](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-108-320.jpg)
![Data Structures & Algorithms
100
if(rear == MAX-1){
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
int removeData(){
int data = intArray[front++];
if(front == MAX){
front = 0;
}
itemCount--;
return data;
}
int main() {
/* insert 5 items */
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
// front : 0
// rear : 4
// ------------------
// index : 0 1 2 3 4
// ------------------
// queue : 3 5 9 1 12
insert(15);
// front : 0
// rear : 5](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-109-320.jpg)



![Data Structures & Algorithms
104
Linear search is a very simple search algorithm. In this type of search, a sequential search
is made over all items one by one. Every item is checked and if a match is found then that
particular item is returned, otherwise the search continues till the end of the data
collection.
Algorithm
Linear Search ( Array A, Value x)
Step 1: Set i to 1
Step 2: if i > n then go to step 7
Step 3: if A[i] = x then go to step 6
Step 4: Set i to i + 1
Step 5: Go to Step 2
Step 6: Print Element x Found at index i and go to step 8
Step 7: Print element not found
Step 8: Exit
Pseudocode
procedure linear_search (list, value)
for each item in the list
if match item == value
return the item's location
16. Linear Search](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-113-320.jpg)
![Data Structures & Algorithms
105
end if
end for
end procedure
To know about linear search implementation in C programming language, please click-
here.
LinearSearchPrograminC
Here we present the implementation of linear search in C programming language. The
output of the program is given after the code.
Linear Search Program
#include <stdio.h>
#define MAX 20
// array of items on which linear search will be conducted.
int intArray[MAX] = {1,2,3,4,6,7,9,11,12,14,15,16,17,19,33,34,43,45,55,66};
void printline(int count){
int i;
for(i = 0;i <count-1;i++){
printf("=");
}
printf("=n");
}
// this method makes a linear search.
int find(int data){
int comparisons = 0;
int index = -1;
int i;](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-114-320.jpg)
![Data Structures & Algorithms
106
// navigate through all items
for(i = 0;i<MAX;i++){
// count the comparisons made
comparisons++;
// if data found, break the loop
if(data == intArray[i]){
index = i;
break;
}
}
printf("Total comparisons made: %d", comparisons);
return index;
}
void display(){
int i;
printf("[");
// navigate through all items
for(i = 0;i<MAX;i++){
printf("%d ",intArray[i]);
}
printf("]n");
}
main(){
printf("Input Array: ");
display();
printline(50);](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-115-320.jpg)
![Data Structures & Algorithms
107
//find location of 1
int location = find(55);
// if element was found
if(location != -1)
printf("nElement found at location: %d" ,(location+1));
else
printf("Element not found.");
}
If we compile and run the above program, it will produce the following result −
Input Array: [1 2 3 4 6 7 9 11 12 14 15 16 17 19 33 34 43 45 55 66 ]
==================================================
Total comparisons made: 19
Element found at location: 19](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-116-320.jpg)


![Data Structures & Algorithms
110
Pseudocode
The pseudocode of binary search algorithms should look like this −
Procedure binary_search
A ← sorted array
n ← size of array
x ← value ot be searched
Set lowerBound = 1
Set upperBound = n
while x not found
if upperBound < lowerBound
EXIT: x does not exists.
set midPoint = lowerBound + ( upperBound - lowerBound ) / 2
if A[midPoint] < x
set lowerBound = midPoint + 1
if A[midPoint] > x
set upperBound = midPoint - 1
if A[midPoint] = x
EXIT: x found at location midPoint
end while
end procedure
To know about binary search implementation using array in C programming language,
please click here.](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-119-320.jpg)
![Data Structures & Algorithms
111
BinarySearchPrograminC
Binary search is a fast search algorithm with run-time complexity of Ο(log n). This search
algorithm works on the principle of divide and conquer. For this algorithm to work properly,
the data collection should be in a sorted form.
Implementation in C
#include <stdio.h>
#define MAX 20
// array of items on which linear search will be conducted.
int intArray[MAX] = {1,2,3,4,6,7,9,11,12,14,15,16,17,19,33,34,43,45,55,66};
void printline(int count){
int i;
for(i = 0;i <count-1;i++){
printf("=");
}
printf("=n");
}
int find(int data){
int lowerBound = 0;
int upperBound = MAX -1;
int midPoint = -1;
int comparisons = 0;
int index = -1;
while(lowerBound <= upperBound){
printf("Comparison %dn" , (comparisons +1) ) ;
printf("lowerBound : %d, intArray[%d] = %dn",
lowerBound,lowerBound,intArray[lowerBound]);
printf("upperBound : %d, intArray[%d] = %dn",
upperBound,upperBound,intArray[upperBound]);](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-120-320.jpg)
![Data Structures & Algorithms
112
comparisons++;
// compute the mid point
// midPoint = (lowerBound + upperBound) / 2;
midPoint = lowerBound + (upperBound - lowerBound) / 2;
// data found
if(intArray[midPoint] == data){
index = midPoint;
break;
}else {
// if data is larger
if(intArray[midPoint] < data){
// data is in upper half
lowerBound = midPoint + 1;
}
// data is smaller
else{
// data is in lower half
upperBound = midPoint -1;
}
}
}
printf("Total comparisons made: %d" , comparisons);
return index;
}
void display(){
int i;
printf("[");
// navigate through all items
for(i = 0;i<MAX;i++){
printf("%d ",intArray[i]);
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-121-320.jpg)
![Data Structures & Algorithms
113
printf("]n");
}
main(){
printf("Input Array: ");
display();
printline(50);
//find location of 1
int location = find(55);
// if element was found
if(location != -1)
printf("nElement found at location: %d" ,(location+1));
else
printf("nElement not found.");
}
If we compile and run the above program, it will produce the following result −
Input Array: [1 2 3 4 6 7 9 11 12 14 15 16 17 19 33 34 43 45 55 66 ]
==================================================
Comparison 1
lowerBound : 0, intArray[0] = 1
upperBound : 19, intArray[19] = 66
Comparison 2
lowerBound : 10, intArray[10] = 15
upperBound : 19, intArray[19] = 66
Comparison 3
lowerBound : 15, intArray[15] = 34
upperBound : 19, intArray[19] = 66
Comparison 4
lowerBound : 18, intArray[18] = 55
upperBound : 19, intArray[19] = 66
Total comparisons made: 4
Element found at location: 19](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-122-320.jpg)


![Data Structures & Algorithms
116
PositionProbinginInterpolationSearch
Interpolation search finds a particular item by computing the probe position. Initially, the
probe position is the position of the middle most item of the collection.
If a match occurs, then the index of the item is returned. To split the list into two parts,
we use the following method −
mid = Lo + ((Hi - Lo) / (A[Hi] - A[Lo])) * (X - A[Lo])
where −
A = list
Lo = Lowest index of the list
Hi = Highest index of the list
A[n] = Value stored at index n in the list
If the middle item is greater than the item, then the probe position is again calculated in
the sub-array to the right of the middle item. Otherwise, the item is searched in the sub-
array to the left of the middle item. This process continues on the sub-array as well until
the size of subarray reduces to zero.
Runtime complexity of interpolation search algorithm is Ο(log (log n)) as compared
to Ο(log n) of BST in favorable situations.
Algorithm
As it is an improvisation of the existing BST algorithm, we are mentioning the steps to
search the 'target' data value index, using position probing −
Step 1 − Start searching data from middle of the list.
Step 2 − If it is a match, return the index of the item, and exit.
Step 3 − If it is not a match, probe position.
Step 4 − Divide the list using probing formula and find the new middle.
Step 5 − If data is greater than middle, search in higher sub-list.
Step 6 − If data is smaller than middle, search in lower sub-list.
Step 7 − Repeat until match.](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-125-320.jpg)
![Data Structures & Algorithms
117
Pseudocode
A → Array list
N → Size of A
X → Target Value
Procedure Interpolation_Search()
Set Lo → 0
Set Mid → -1
Set Hi → N-1
While X does not match
if Lo equals to Hi OR A[Lo] equals to A[Hi]
EXIT: Failure, Target not found
end if
Set Mid = Lo + ((Hi - Lo) / (A[Hi] - A[Lo])) * (X - A[Lo])
if A[Mid] = X
EXIT: Success, Target found at Mid
else
if A[Mid] < X
Set Lo to Mid+1
else if A[Mid] > X
Set Hi to Mid-1
end if
end if
End While
End Procedure
To know about the implementation of interpolation search in C programming
language, click here.](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-126-320.jpg)
![Data Structures & Algorithms
118
InterpolationSearchPrograminC
Interpolation search is an improved variant of binary search. This search algorithm works
on the probing position of the required value. For this algorithm to work properly, the data
collection should be in sorted and equally distributed form.
It's runtime complexity is log2(log2 n).
Implementation in C
#include<stdio.h>
#define MAX 10
// array of items on which linear search will be conducted.
int list[MAX] = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44 };
int find(int data) {
int lo = 0;
int hi = MAX - 1;
int mid = -1;
int comparisons = 1;
int index = -1;
while(lo <= hi) {
printf("nComparison %d n" , comparisons ) ;
printf("lo : %d, list[%d] = %dn", lo, lo, list[lo]);
printf("hi : %d, list[%d] = %dn", hi, hi, list[hi]);
comparisons++;
// probe the mid point
mid = lo + (((double)(hi - lo) / (list[hi] - list[lo])) * (data - list[lo]));
printf("mid = %dn",mid);
// data found
if(list[mid] == data) {
index = mid;
break;
}else {](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-127-320.jpg)
![Data Structures & Algorithms
119
if(list[mid] < data) {
// if data is larger, data is in upper half
lo = mid + 1;
}else {
// if data is smaller, data is in lower half
hi = mid - 1;
}
}
}
printf("nTotal comparisons made: %d", --comparisons);
return index;
}
int main() {
//find location of 33
int location = find(33);
// if element was found
if(location != -1)
printf("nElement found at location: %d" ,(location+1));
else
printf("Element not found.");
return 0;
}
If we compile and run the above program, it will produce the following result −
Comparison 1
lo : 0, list[0] = 10
hi : 9, list[9] = 44
mid = 6
Total comparisons made: 1
Element found at location: 7
You can change the search value and execute the program to test it.](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-128-320.jpg)



![Data Structures & Algorithms
123
struct DataItem *search(int key){
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty
while(hashArray[hashIndex] != NULL){
if(hashArray[hashIndex]->key == key)
return hashArray[hashIndex];
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= SIZE;
}
return NULL;
}
InsertOperation
Whenever an element is to be inserted, compute the hash code of the key passed and
locate the index using that hash code as an index in the array. Use linear probing for
empty location, if an element is found at the computed hash code.
void insert(int key,int data){
struct DataItem *item = (struct DataItem*) malloc(sizeof(struct DataItem));
item->data = data;
item->key = key;
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty or deleted cell
while(hashArray[hashIndex] != NULL && hashArray[hashIndex]->key != -1){
//go to next cell
++hashIndex;](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-132-320.jpg)
![Data Structures & Algorithms
124
//wrap around the table
hashIndex %= SIZE;
}
hashArray[hashIndex] = item;
}
DeleteOperation
Whenever an element is to be deleted, compute the hash code of the key passed and
locate the index using that hash code as an index in the array. Use linear probing to get
the element ahead if an element is not found at the computed hash code. When found,
store a dummy item there to keep the performance of the hash table intact.
struct DataItem* delete(struct DataItem* item){
int key = item->key;
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty
while(hashArray[hashIndex] !=NULL){
if(hashArray[hashIndex]->key == key){
struct DataItem* temp = hashArray[hashIndex];
//assign a dummy item at deleted position
hashArray[hashIndex] = dummyItem;
return temp;
}
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= SIZE;
}
return NULL;
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-133-320.jpg)
![Data Structures & Algorithms
125
To know about hash implementation in C programming language, please click here.
HashTablePrograminC
Hash Table is a data structure which stores data in an associative manner. In hash table,
the data is stored in an array format where each data value has its own unique index
value. Access of data becomes very fast, if we know the index of the desired data.
Implementation in C
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define SIZE 20
struct DataItem {
int data;
int key;
};
struct DataItem* hashArray[SIZE];
struct DataItem* dummyItem;
struct DataItem* item;
int hashCode(int key){
return key % SIZE;
}
struct DataItem *search(int key){
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty
while(hashArray[hashIndex] != NULL){
if(hashArray[hashIndex]->key == key)
return hashArray[hashIndex];](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-134-320.jpg)
![Data Structures & Algorithms
126
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= SIZE;
}
return NULL;
}
void insert(int key,int data){
struct DataItem *item = (struct DataItem*) malloc(sizeof(struct DataItem));
item->data = data;
item->key = key;
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty or deleted cell
while(hashArray[hashIndex] != NULL && hashArray[hashIndex]->key != -1){
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= SIZE;
}
hashArray[hashIndex] = item;
}
struct DataItem* delete(struct DataItem* item){
int key = item->key;
//get the hash](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-135-320.jpg)
![Data Structures & Algorithms
127
int hashIndex = hashCode(key);
//move in array until an empty
while(hashArray[hashIndex] != NULL){
if(hashArray[hashIndex]->key == key){
struct DataItem* temp = hashArray[hashIndex];
//assign a dummy item at deleted position
hashArray[hashIndex] = dummyItem;
return temp;
}
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= SIZE;
}
return NULL;
}
void display(){
int i = 0;
for(i = 0; i<SIZE; i++) {
if(hashArray[i] != NULL)
printf(" (%d,%d)",hashArray[i]->key,hashArray[i]->data);
else
printf(" ~~ ");
}
printf("n");
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-136-320.jpg)









![Data Structures & Algorithms
137
Algorithm
We assume list is an array of n elements. We further assume that swap function swaps
the values of the given array elements.
begin BubbleSort(list)
for all elements of list
if list[i] > list[i+1]
swap(list[i], list[i+1])
end if
end for
return list
end BubbleSort
Pseudocode
We observe in algorithm that Bubble Sort compares each pair of array element unless the
whole array is completely sorted in an ascending order. This may cause a few complexity
issues like what if the array needs no more swapping as all the elements are already
ascending.
To ease-out the issue, we use one flag variable swapped which will help us see if any
swap has happened or not. If no swap has occurred, i.e. the array requires no more
processing to be sorted, it will come out of the loop.
Pseudocode of BubbleSort algorithm can be written as follows −
procedure bubbleSort( list : array of items )
loop = list.count;
for i = 0 to loop-1 do:
swapped = false
for j = 0 to loop-1 do:
/* compare the adjacent elements */
if list[j] > list[j+1] then
/* swap them */
swap( list[j], list[j+1] )](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-146-320.jpg)
![Data Structures & Algorithms
138
swapped = true
end if
end for
/*if no number was swapped that means
array is sorted now, break the loop.*/
if(not swapped) then
break
end if
end for
end procedure return list
Implementation
One more issue we did not address in our original algorithm and its improvised
pseudocode, is that, after every iteration the highest values settles down at the end of the
array. Hence, the next iteration need not include already sorted elements. For this
purpose, in our implementation, we restrict the inner loop to avoid already sorted values.
To know about bubble sort implementation in C programming language, please click here.
BubbleSortPrograminC
We shall see the implementation of bubble sort in C programming language here.
Implementation in C
#include <stdio.h>
#include <stdbool.h>
#define MAX 10
int list[MAX] = {1,8,4,6,0,3,5,2,7,9};
void display(){
int i;
printf("[");](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-147-320.jpg)
![Data Structures & Algorithms
139
// navigate through all items
for(i = 0; i < MAX; i++){
printf("%d ",list[i]);
}
printf("]n");
}
void bubbleSort() {
int temp;
int i,j;
bool swapped = false;
// loop through all numbers
for(i = 0; i < MAX-1; i++) {
swapped = false;
// loop through numbers falling ahead
for(j = 0; j < MAX-1-i; j++) {
printf(" Items compared: [ %d, %d ] ", list[j],list[j+1]);
// check if next number is lesser than current no
// swap the numbers.
// (Bubble up the highest number)
if(list[j] > list[j+1]) {
temp = list[j];
list[j] = list[j+1];
list[j+1] = temp;
swapped = true;
printf(" => swapped [%d, %d]n",list[j],list[j+1]);
}else {
printf(" => not swappedn");
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-148-320.jpg)
![Data Structures & Algorithms
140
}
// if no number was swapped that means
// array is sorted now, break the loop.
if(!swapped) {
break;
}
printf("Iteration %d#: ",(i+1));
display();
}
}
main(){
printf("Input Array: ");
display();
printf("n");
bubbleSort();
printf("nOutput Array: ");
display();
}
If we compile and run the above program, it will produce the following result −
Input Array: [1 8 4 6 0 3 5 2 7 9 ]
Items compared: [ 1, 8 ] => not swapped
Items compared: [ 8, 4 ] => swapped [4, 8]
Items compared: [ 8, 6 ] => swapped [6, 8]
Items compared: [ 8, 0 ] => swapped [0, 8]
Items compared: [ 8, 3 ] => swapped [3, 8]
Items compared: [ 8, 5 ] => swapped [5, 8]
Items compared: [ 8, 2 ] => swapped [2, 8]
Items compared: [ 8, 7 ] => swapped [7, 8]
Items compared: [ 8, 9 ] => not swapped](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-149-320.jpg)
![Data Structures & Algorithms
141
Iteration 1#: [1 4 6 0 3 5 2 7 8 9 ]
Items compared: [ 1, 4 ] => not swapped
Items compared: [ 4, 6 ] => not swapped
Items compared: [ 6, 0 ] => swapped [0, 6]
Items compared: [ 6, 3 ] => swapped [3, 6]
Items compared: [ 6, 5 ] => swapped [5, 6]
Items compared: [ 6, 2 ] => swapped [2, 6]
Items compared: [ 6, 7 ] => not swapped
Items compared: [ 7, 8 ] => not swapped
Iteration 2#: [1 4 0 3 5 2 6 7 8 9 ]
Items compared: [ 1, 4 ] => not swapped
Items compared: [ 4, 0 ] => swapped [0, 4]
Items compared: [ 4, 3 ] => swapped [3, 4]
Items compared: [ 4, 5 ] => not swapped
Items compared: [ 5, 2 ] => swapped [2, 5]
Items compared: [ 5, 6 ] => not swapped
Items compared: [ 6, 7 ] => not swapped
Iteration 3#: [1 0 3 4 2 5 6 7 8 9 ]
Items compared: [ 1, 0 ] => swapped [0, 1]
Items compared: [ 1, 3 ] => not swapped
Items compared: [ 3, 4 ] => not swapped
Items compared: [ 4, 2 ] => swapped [2, 4]
Items compared: [ 4, 5 ] => not swapped
Items compared: [ 5, 6 ] => not swapped
Iteration 4#: [0 1 3 2 4 5 6 7 8 9 ]
Items compared: [ 0, 1 ] => not swapped
Items compared: [ 1, 3 ] => not swapped
Items compared: [ 3, 2 ] => swapped [2, 3]
Items compared: [ 3, 4 ] => not swapped
Items compared: [ 4, 5 ] => not swapped
Iteration 5#: [0 1 2 3 4 5 6 7 8 9 ]
Items compared: [ 0, 1 ] => not swapped
Items compared: [ 1, 2 ] => not swapped
Items compared: [ 2, 3 ] => not swapped
Items compared: [ 3, 4 ] => not swapped
Output Array: [0 1 2 3 4 5 6 7 8 9 ]](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-150-320.jpg)


![Data Structures & Algorithms
144
We swap them again. By the end of third iteration, we have a sorted sub-list of 4 items.
This process goes on until all the unsorted values are covered in a sorted sub-list. Now we
shall see some programming aspects of insertion sort.
Algorithm
Now we have a bigger picture of how this sorting technique works, so we can derive simple
steps by which we can achieve insertion sort.
Step 1 − If it is the first element, it is already sorted. return 1;
Step 2 − Pick next element
Step 3 − Compare with all elements in the sorted sub-list
Step 4 − Shift all the elements in the sorted sub-list that is greater than the
value to be sorted
Step 5 − Insert the value
Step 6 − Repeat until list is sorted
Pseudocode
procedure insertionSort( A : array of items )
int holePosition
int valueToInsert
for i = 1 to length(A) inclusive do:
/* select value to be inserted */
valueToInsert = A[i]
holePosition = i](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-153-320.jpg)
![Data Structures & Algorithms
145
/*locate hole position for the element to be inserted */
while holePosition > 0 and A[holePosition-1] > valueToInsert do:
A[holePosition] = A[holePosition-1]
holePosition = holePosition -1
end while
/* insert the number at hole position */
A[holePosition] = valueToInsert
end for
end procedure
To know about insertion sort implementation in C programming language, please click
here.
InsertionSortPrograminC
This is an in-place comparison-based sorting algorithm. Here, a sub-list is maintained
which is always sorted. For example, the lower part of an array is maintained to be sorted.
An element which is to be 'insert'ed in this sorted sub-list, has to find its appropriate place
and then it is to be inserted there. Hence the name insertion sort.
Implementation in C
#include <stdio.h>
#include <stdbool.h>
#define MAX 7
int intArray[MAX] = {4,6,3,2,1,9,7};
void printline(int count){
int i;
for(i = 0;i <count-1;i++){
printf("=");
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-154-320.jpg)
![Data Structures & Algorithms
146
printf("=n");
}
void display(){
int i;
printf("[");
// navigate through all items
for(i = 0;i<MAX;i++){
printf("%d ",intArray[i]);
}
printf("]n");
}
void insertionSort(){
int valueToInsert;
int holePosition;
int i;
// loop through all numbers
for(i = 1; i < MAX; i++){
// select a value to be inserted.
valueToInsert = intArray[i];
// select the hole position where number is to be inserted
holePosition = i;
// check if previous no. is larger than value to be inserted
while (holePosition > 0 && intArray[holePosition-1] > valueToInsert){
intArray[holePosition] = intArray[holePosition-1];
holePosition--;
printf(" item moved : %dn" , intArray[holePosition]);
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-155-320.jpg)
![Data Structures & Algorithms
147
if(holePosition != i){
printf(" item inserted : %d, at position : %dn" ,
valueToInsert,holePosition);
// insert the number at hole position
intArray[holePosition] = valueToInsert;
}
printf("Iteration %d#:",i);
display();
}
}
main(){
printf("Input Array: ");
display();
printline(50);
insertionSort();
printf("Output Array: ");
display();
printline(50);
}
If we compile and run the above program, it will produce the following result −
Input Array: [4 6 3 2 1 9 7 ]
==================================================
Iteration 1#:[4 6 3 2 1 9 7 ]
item moved : 6
item moved : 4
item inserted : 3, at position : 0
Iteration 2#:[3 4 6 2 1 9 7 ]
item moved : 6
item moved : 4
item moved : 3
item inserted : 2, at position : 0
Iteration 3#:[2 3 4 6 1 9 7 ]
item moved : 6](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-156-320.jpg)
![Data Structures & Algorithms
148
item moved : 4
item moved : 3
item moved : 2
item inserted : 1, at position : 0
Iteration 4#:[1 2 3 4 6 9 7 ]
Iteration 5#:[1 2 3 4 6 9 7 ]
item moved : 9
item inserted : 7, at position : 5
Iteration 6#:[1 2 3 4 6 7 9 ]
Output Array: [1 2 3 4 6 7 9 ]
==================================================](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-157-320.jpg)

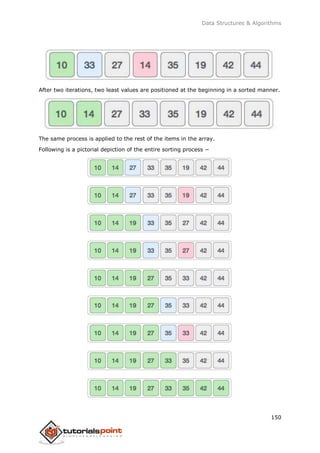
![Data Structures & Algorithms
151
Now, let us learn some programming aspects of selection sort.
Algorithm
Step 1 − Set MIN to location 0
Step 2 − Search the minimum element in the list
Step 3 − Swap with value at location MIN
Step 4 − Increment MIN to point to next element
Step 5 − Repeat until list is sorted
Pseudocode
procedure selection sort
list : array of items
n : size of list
for i = 1 to n - 1
/* set current element as minimum*/
min = i
/* check the element to be minimum */
for j = i+1 to n
if list[j] < list[min] then
min = j;
end if
end for
/* swap the minimum element with the current element*/
if indexMin != i then
swap list[min] and list[i]
end if
end for
end procedure
To know about selection sort implementation in C programming language, please click
here.](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-160-320.jpg)
![Data Structures & Algorithms
152
SelectionSortPrograminC
Selection sort is a simple sorting algorithm. This sorting algorithm is an in-place
comparison-based algorithm in which the list is divided into two parts, the sorted part at
the left end and the unsorted part at the right end. Initially, the sorted part is empty and
the unsorted part is the entire list.
Implementation in C
#include <stdio.h>
#include <stdbool.h>
#define MAX 7
int intArray[MAX] = {4,6,3,2,1,9,7};
void printline(int count){
int i;
for(i = 0;i <count-1;i++){
printf("=");
}
printf("=n");
}
void display(){
int i;
printf("[");
// navigate through all items
for(i = 0;i<MAX;i++){
printf("%d ", intArray[i]);
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-161-320.jpg)
![Data Structures & Algorithms
153
printf("]n");
}
void selectionSort(){
int indexMin,i,j;
// loop through all numbers
for(i = 0; i < MAX-1; i++){
// set current element as minimum
indexMin = i;
// check the element to be minimum
for(j = i+1;j<MAX;j++){
if(intArray[j] < intArray[indexMin]){
indexMin = j;
}
}
if(indexMin != i){
printf("Items swapped: [ %d, %d ]n" , intArray[i],
intArray[indexMin]);
// swap the numbers
int temp = intArray[indexMin];
intArray[indexMin] = intArray[i];
intArray[i] = temp;
}
printf("Iteration %d#:",(i+1));
display();
}
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-162-320.jpg)
![Data Structures & Algorithms
154
main(){
printf("Input Array: ");
display();
printline(50);
selectionSort();
printf("Output Array: ");
display();
printline(50);
}
If we compile and run the above program, it will produce the following result −
Input Array: [4 6 3 2 1 9 7 ]
==================================================
Items swapped: [ 4, 1 ]
Iteration 1#:[1 6 3 2 4 9 7 ]
Items swapped: [ 6, 2 ]
Iteration 2#:[1 2 3 6 4 9 7 ]
Iteration 3#:[1 2 3 6 4 9 7 ]
Items swapped: [ 6, 4 ]
Iteration 4#:[1 2 3 4 6 9 7 ]
Iteration 5#:[1 2 3 4 6 9 7 ]
Items swapped: [ 9, 7 ]
Iteration 6#:[1 2 3 4 6 7 9 ]
Output Array: [1 2 3 4 6 7 9 ]
==================================================](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-163-320.jpg)

![Data Structures & Algorithms
156
In the next iteration of the combining phase, we compare lists of two data values, and
merge them into a list of found data values placing all in a sorted order.
After the final merging, the list should look like this −
Now we should learn some programming aspects of merge sorting.
Algorithm
Merge sort keeps on dividing the list into equal halves until it can no more be divided. By
definition, if it is only one element in the list, it is sorted. Then, merge sort combines the
smaller sorted lists keeping the new list sorted too.
Step 1 − if it is only one element in the list it is already sorted, return.
Step 2 − divide the list recursively into two halves until it can no more be
divided.
Step 3 − merge the smaller lists into new list in sorted order.
Pseudocode
We shall now see the pseudocodes for merge sort functions. As our algorithms point out
two main functions − divide & merge.
Merge sort works with recursion and we shall see our implementation in the same way.
procedure mergesort( var a as array )
if ( n == 1 ) return a
var l1 as array = a[0] ... a[n/2]
var l2 as array = a[n/2+1] ... a[n]
l1 = mergesort( l1 )](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-165-320.jpg)
![Data Structures & Algorithms
157
l2 = mergesort( l2 )
return merge( l1, l2 )
end procedure
procedure merge( var a as array, var b as array )
var c as array
while ( a and b have elements )
if ( a[0] > b[0] )
add b[0] to the end of c
remove b[0] from b
else
add a[0] to the end of c
remove a[0] from a
end if
end while
while ( a has elements )
add a[0] to the end of c
remove a[0] from a
end while
while ( b has elements )
add b[0] to the end of c
remove b[0] from b
end while
return c
end procedure
To know about merge sort implementation in C programming language, please click here.](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-166-320.jpg)
![Data Structures & Algorithms
158
MergeSortPrograminC
Merge sort is a sorting technique based on divide and conquer technique. With the worst-
case time complexity being Ο(n log n), it is one of the most respected algorithms.
Implementation in C
We shall see the implementation of merge sort in C programming language here −
#include <stdio.h>
#define max 10
int a[10] = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44 };
int b[10];
void merging(int low, int mid, int high) {
int l1, l2, i;
for(l1 = low, l2 = mid + 1, i = low; l1 <= mid && l2 <= high; i++) {
if(a[l1] <= a[l2])
b[i] = a[l1++];
else
b[i] = a[l2++];
}
while(l1 <= mid)
b[i++] = a[l1++];
while(l2 <= high)
b[i++] = a[l2++];
for(i = low; i <= high; i++)
a[i] = b[i];
}
void sort(int low, int high) {
int mid;
if(low < high) {](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-167-320.jpg)
![Data Structures & Algorithms
159
mid = (low + high) / 2;
sort(low, mid);
sort(mid+1, high);
merging(low, mid, high);
}else {
return;
}
}
int main() {
int i;
printf("List before sortingn");
for(i = 0; i <= max; i++)
printf("%d ", a[i]);
sort(0, max);
printf("nList after sortingn");
for(i = 0; i <= max; i++)
printf("%d ", a[i]);
}
If we compile and run the above program, it will produce the following result −
List before sorting
10 14 19 26 27 31 33 35 42 44 0
List after sorting
0 10 14 19 26 27 31 33 35 42 44](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-168-320.jpg)



![Data Structures & Algorithms
163
We see that it required only four swaps to sort the rest of the array.
Algorithm
Following is the algorithm for shell sort.
Step 1 − Initialize the value of h
Step 2 − Divide the list into smaller sub-list of equal interval h
Step 3 − Sort these sub-lists using insertion sort
Step 3 − Repeat until complete list is sorted
Pseudocode
Following is the pseudocode for shell sort.
procedure shellSort()
A : array of items
/* calculate interval*/
while interval < A.length /3 do:
interval = interval * 3 + 1
end while
while interval > 0 do:
for outer = interval; outer < A.length; outer ++ do:
/* select value to be inserted */
valueToInsert = A[outer]
inner = outer;
/*shift element towards right*/
while inner > interval -1 && A[inner - interval] >= valueToInsert do:
A[inner] = A[inner - interval]
inner = inner - interval
end while](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-172-320.jpg)
![Data Structures & Algorithms
164
/* insert the number at hole position */
A[inner] = valueToInsert
end for
/* calculate interval*/
interval = (interval -1) /3;
end while
end procedure
To know about shell sort implementation in C programming language, please click here.
ShellSortPrograminC
Shell sort is a highly efficient sorting algorithm and is based on insertion sort algorithm.
This algorithm avoids large shifts as in case of insertion sort, if the smaller value is to the
far right and has to be moved to the far left.
Implementation in C
#include <stdio.h>
#include <stdbool.h>
#define MAX 7
int intArray[MAX] = {4,6,3,2,1,9,7};
void printline(int count){
int i;
for(i = 0;i <count-1;i++){
printf("=");
}
printf("=n");
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-173-320.jpg)
![Data Structures & Algorithms
165
void display(){
int i;
printf("[");
// navigate through all items
for(i = 0;i<MAX;i++){
printf("%d ",intArray[i]);
}
printf("]n");
}
void shellSort(){
int inner, outer;
int valueToInsert;
int interval = 1;
int elements = MAX;
int i = 0;
while(interval <= elements/3) {
interval = interval*3 +1;
}
while(interval > 0) {
printf("iteration %d#:",i);
display();
for(outer = interval; outer < elements; outer++) {
valueToInsert = intArray[outer];
inner = outer;
while(inner > interval -1 && intArray[inner - interval]
>= valueToInsert) {
intArray[inner] = intArray[inner - interval];
inner -=interval;
printf(" item moved :%dn",intArray[inner]);
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-174-320.jpg)
![Data Structures & Algorithms
166
intArray[inner] = valueToInsert;
printf(" item inserted :%d, at position :%dn",valueToInsert,inner);
}
interval = (interval -1) /3;
i++;
}
}
int main() {
printf("Input Array: ");
display();
printline(50);
shellSort();
printf("Output Array: ");
display();
printline(50);
return 1;
}
If we compile and run the above program, it will produce the following result −
Input Array: [4 6 3 2 1 9 7 ]
==================================================
iteration 0#:[4 6 3 2 1 9 7 ]
item moved :4
item inserted :1, at position :0
item inserted :9, at position :5
item inserted :7, at position :6
iteration 1#:[1 6 3 2 4 9 7 ]
item inserted :6, at position :1
item moved :6
item inserted :3, at position :1
item moved :6](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-175-320.jpg)
![Data Structures & Algorithms
167
item moved :3
item inserted :2, at position :1
item moved :6
item inserted :4, at position :3
item inserted :9, at position :5
item moved :9
item inserted :7, at position :5
Output Array: [1 2 3 4 6 7 9 ]
==================================================](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-176-320.jpg)

![Data Structures & Algorithms
169
QuickSortPivotPseudocode
The pseudocode for the above algorithm can be derived as −
function partitionFunc(left, right, pivot)
leftPointer = left -1
rightPointer = right
while True do
while A[++leftPointer] < pivot do
//do-nothing
end while
while rightPointer > 0 && A[--rightPointer] > pivot do
//do-nothing
end while
if leftPointer >= rightPointer
break
else
swap leftPointer,rightPointer
end if
end while
swap leftPointer,right
return leftPointer
end function
QuickSortAlgorithm
Using pivot algorithm recursively, we end up with smaller possible partitions. Each
partition is then processed for quick sort. We define recursive algorithm for quicksort as
follows −
Step 1 − Make the right-most index value pivot
Step 2 − partition the array using pivot value
Step 3 − quicksort left partition recursively
Step 4 − quicksort right partition recursively](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-178-320.jpg)
![Data Structures & Algorithms
170
QuickSortPseudocode
To get more into it, let see the pseudocode for quick sort algorithm −
procedure quickSort(left, right)
if right-left <= 0
return
else
pivot = A[right]
partition = partitionFunc(left, right, pivot)
quickSort(left,partition-1)
quickSort(partition+1,right)
end if
end procedure
To know about quick sort implementation in C programming language, please click here.
QuickSortPrograminC
Quick sort is a highly efficient sorting algorithm and is based on partitioning of array of
data into smaller arrays. A large array is partitioned into two arrays one of which holds
values smaller than the specified value, say pivot, based on which the partition is made
and another array holds values greater than the pivot value.
Implementation in C
#include <stdio.h>
#include <stdbool.h>
#define MAX 7
int intArray[MAX] = {4,6,3,2,1,9,7};
void printline(int count){
int i;
for(i = 0;i <count-1;i++){
printf("=");
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-179-320.jpg)
![Data Structures & Algorithms
171
printf("=n");
}
void display(){
int i;
printf("[");
// navigate through all items
for(i = 0;i<MAX;i++){
printf("%d ",intArray[i]);
}
printf("]n");
}
void swap(int num1, int num2){
int temp = intArray[num1];
intArray[num1] = intArray[num2];
intArray[num2] = temp;
}
int partition(int left, int right, int pivot){
int leftPointer = left -1;
int rightPointer = right;
while(true){
while(intArray[++leftPointer] < pivot){
//do nothing
}
while(rightPointer > 0 && intArray[--rightPointer] > pivot){
//do nothing
}
if(leftPointer >= rightPointer){
break;
}else{](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-180-320.jpg)
![Data Structures & Algorithms
172
printf(" item swapped :%d,%dn",
intArray[leftPointer],intArray[rightPointer]);
swap(leftPointer,rightPointer);
}
}
printf(" pivot swapped :%d,%dn", intArray[leftPointer],intArray[right]);
swap(leftPointer,right);
printf("Updated Array: ");
display();
return leftPointer;
}
void quickSort(int left, int right){
if(right-left <= 0){
return;
}else {
int pivot = intArray[right];
int partitionPoint = partition(left, right, pivot);
quickSort(left,partitionPoint-1);
quickSort(partitionPoint+1,right);
}
}
main(){
printf("Input Array: ");
display();
printline(50);
quickSort(0,MAX-1);
printf("Output Array: ");
display();
printline(50);
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-181-320.jpg)
![Data Structures & Algorithms
173
If we compile and run the above program, it will produce the following result −
Input Array: [4 6 3 2 1 9 7 ]
==================================================
pivot swapped :9,7
Updated Array: [4 6 3 2 1 7 9 ]
pivot swapped :4,1
Updated Array: [1 6 3 2 4 7 9 ]
item swapped :6,2
pivot swapped :6,4
Updated Array: [1 2 3 4 6 7 9 ]
pivot swapped :3,3
Updated Array: [1 2 3 4 6 7 9 ]
Output Array: [1 2 3 4 6 7 9 ]
==================================================](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-182-320.jpg)






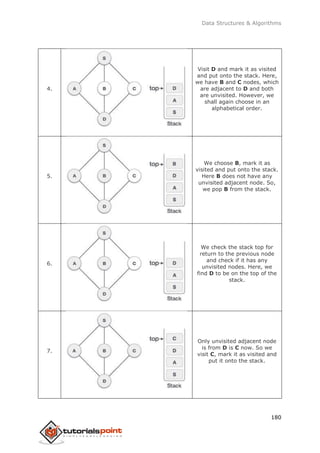

![Data Structures & Algorithms
182
//stack variables
int stack[MAX];
int top = -1;
//graph variables
//array of vertices
struct Vertex* lstVertices[MAX];
//adjacency matrix
int adjMatrix[MAX][MAX];
//vertex count
int vertexCount = 0;
//stack functions
void push(int item) {
stack[++top] = item;
}
int pop() {
return stack[top--];
}
int peek() {
return stack[top];
}
bool isStackEmpty() {
return top == -1;
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-191-320.jpg)
![Data Structures & Algorithms
183
//graph functions
//add vertex to the vertex list
void addVertex(char label) {
struct Vertex* vertex = (struct Vertex*) malloc(sizeof(struct Vertex));
vertex->label = label;
vertex->visited = false;
lstVertices[vertexCount++] = vertex;
}
//add edge to edge array
void addEdge(int start,int end) {
adjMatrix[start][end] = 1;
adjMatrix[end][start] = 1;
}
//display the vertex
void displayVertex(int vertexIndex) {
printf("%c ",lstVertices[vertexIndex]->label);
}
//get the adjacent unvisited vertex
int getAdjUnvisitedVertex(int vertexIndex) {
int i;
for(i = 0; i<vertexCount; i++) {
if(adjMatrix[vertexIndex][i] == 1 && lstVertices[i]->visited == false) {
return i;
}
}
return -1;
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-192-320.jpg)
![Data Structures & Algorithms
184
void depthFirstSearch() {
int i;
//mark first node as visited
lstVertices[0]->visited = true;
//display the vertex
displayVertex(0);
//push vertex index in stack
push(0);
while(!isStackEmpty()) {
//get the unvisited vertex of vertex which is at top of the stack
int unvisitedVertex = getAdjUnvisitedVertex(peek());
//no adjacent vertex found
if(unvisitedVertex == -1) {
pop();
}else {
lstVertices[unvisitedVertex]->visited = true;
displayVertex(unvisitedVertex);
push(unvisitedVertex);
}
}
//stack is empty, search is complete, reset the visited flag
for(i = 0;i < vertexCount;i++) {
lstVertices[i]->visited = false;
}
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-193-320.jpg)
![Data Structures & Algorithms
185
int main() {
int i, j;
for(i = 0; i<MAX; i++) // set adjacency {
for(j = 0; j<MAX; j++) // matrix to 0
adjMatrix[i][j] = 0;
}
addVertex('S'); // 0
addVertex('A'); // 1
addVertex('B'); // 2
addVertex('C'); // 3
addVertex('D'); // 4
addEdge(0, 1); // S - A
addEdge(0, 2); // S - B
addEdge(0, 3); // S - C
addEdge(1, 4); // A - D
addEdge(2, 4); // B - D
addEdge(3, 4); // C - D
printf("Depth First Search: ");
depthFirstSearch();
return 0;
}
If we compile and run the above program, it will produce the following result −
Depth First Search: S A D B C](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-194-320.jpg)
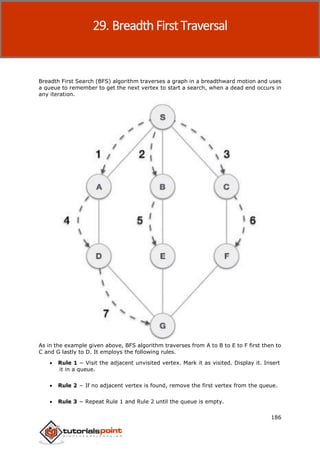


![Data Structures & Algorithms
189
Implementation in C
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 5
struct Vertex {
char label;
bool visited;
};
//queue variables
int queue[MAX];
int rear = -1;
int front = 0;
int queueItemCount = 0;
//graph variables](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-198-320.jpg)
![Data Structures & Algorithms
190
//array of vertices
struct Vertex* lstVertices[MAX];
//adjacency matrix
int adjMatrix[MAX][MAX];
//vertex count
int vertexCount = 0;
//queue functions
void insert(int data) {
queue[++rear] = data;
queueItemCount++;
}
int removeData() {
queueItemCount--;
return queue[front++];
}
bool isQueueEmpty() {
return queueItemCount == 0;
}
//graph functions
//add vertex to the vertex list
void addVertex(char label) {
struct Vertex* vertex = (struct Vertex*) malloc(sizeof(struct Vertex));
vertex->label = label;
vertex->visited = false;
lstVertices[vertexCount++] = vertex;
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-199-320.jpg)
![Data Structures & Algorithms
191
//add edge to edge array
void addEdge(int start,int end) {
adjMatrix[start][end] = 1;
adjMatrix[end][start] = 1;
}
//display the vertex
void displayVertex(int vertexIndex) {
printf("%c ",lstVertices[vertexIndex]->label);
}
//get the adjacent unvisited vertex
int getAdjUnvisitedVertex(int vertexIndex) {
int i;
for(i = 0; i<vertexCount; i++) {
if(adjMatrix[vertexIndex][i] == 1 && lstVertices[i]->visited == false)
return i;
}
return -1;
}
void breadthFirstSearch() {
int i;
//mark first node as visited
lstVertices[0]->visited = true;
//display the vertex
displayVertex(0);](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-200-320.jpg)
![Data Structures & Algorithms
192
//insert vertex index in queue
insert(0);
int unvisitedVertex;
while(!isQueueEmpty()) {
//get the unvisited vertex of vertex which is at front of the queue
int tempVertex = removeData();
//no adjacent vertex found
while((unvisitedVertex = getAdjUnvisitedVertex(tempVertex)) != -1) {
lstVertices[unvisitedVertex]->visited = true;
displayVertex(unvisitedVertex);
insert(unvisitedVertex);
}
}
//queue is empty, search is complete, reset the visited flag
for(i = 0;i<vertexCount;i++) {
lstVertices[i]->visited = false;
}
}
int main() {
int i, j;
for(i = 0; i<MAX; i++) // set adjacency {
for(j = 0; j<MAX; j++) // matrix to 0
adjMatrix[i][j] = 0;
}
addVertex('S'); // 0
addVertex('A'); // 1
addVertex('B'); // 2
addVertex('C'); // 3
addVertex('D'); // 4](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-201-320.jpg)








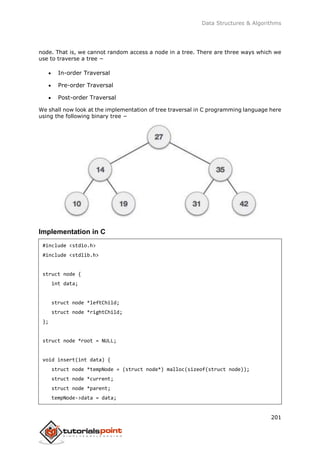


![Data Structures & Algorithms
204
}
}
void post_order_traversal(struct node* root) {
if(root != NULL) {
post_order_traversal(root->leftChild);
post_order_traversal(root->rightChild);
printf("%d ", root->data);
}
}
int main() {
int i;
int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
for(i = 0; i < 7; i++)
insert(array[i]);
i = 31;
struct node * temp = search(i);
if(temp != NULL) {
printf("[%d] Element found.", temp->data);
printf("n");
}else {
printf("[ x ] Element not found (%d).n", i);
}
i = 15;
temp = search(i);
if(temp != NULL) {
printf("[%d] Element found.", temp->data);
printf("n");
}else {
printf("[ x ] Element not found (%d).n", i);
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-213-320.jpg)
![Data Structures & Algorithms
205
printf("nPreorder traversal: ");
pre_order_traversal(root);
printf("nInorder traversal: ");
inorder_traversal(root);
printf("nPost order traversal: ");
post_order_traversal(root);
return 0;
}
If we compile and run the above program, it will produce the following result −
Visiting elements: 27 35 [31] Element found.
Visiting elements: 27 14 19 [ x ] Element not found (15).
Preorder traversal: 27 14 10 19 35 31 42
Inorder traversal: 10 14 19 27 31 35 42
Post order traversal: 10 19 14 31 42 35 27](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-214-320.jpg)



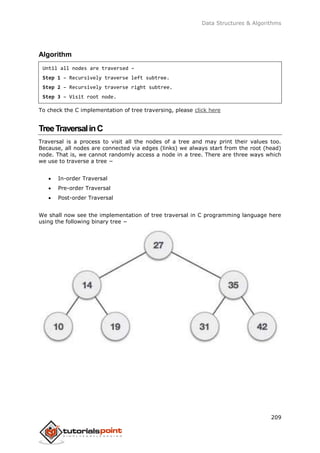



![Data Structures & Algorithms
213
int i;
int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
for(i = 0; i < 7; i++)
insert(array[i]);
i = 31;
struct node * temp = search(i);
if(temp != NULL) {
printf("[%d] Element found.", temp->data);
printf("n");
}else {
printf("[ x ] Element not found (%d).n", i);
}
i = 15;
temp = search(i);
if(temp != NULL) {
printf("[%d] Element found.", temp->data);
printf("n");
}else {
printf("[ x ] Element not found (%d).n", i);
}
printf("nPreorder traversal: ");
pre_order_traversal(root);
printf("nInorder traversal: ");
inorder_traversal(root);
printf("nPost order traversal: ");
post_order_traversal(root);
return 0;
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-222-320.jpg)
![Data Structures & Algorithms
214
If we compile and run the above program, it will produce the following result −
Visiting elements: 27 35 [31] Element found.
Visiting elements: 27 14 19 [ x ] Element not found (15).
Preorder traversal: 27 14 10 19 35 31 42
Inorder traversal: 10 14 19 27 31 35 42
Post order traversal: 10 19 14 31 42 35 27](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-223-320.jpg)


























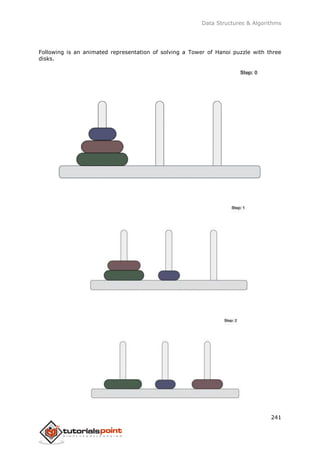





![Data Structures & Algorithms
247
TowerofHanoiinC
Program
#include <stdio.h>
#include <stdbool.h>
#define MAX 10
int list[MAX] = {1,8,4,6,0,3,5,2,7,9};
void display(){
int i;
printf("[");
// navigate through all items
for(i = 0; i < MAX; i++){
printf("%d ",list[i]);
}
printf("]n");
}
void bubbleSort() {
int temp;
int i,j;
bool swapped = false;
// loop through all numbers
for(i = 0; i < MAX-1; i++) {
swapped = false;
// loop through numbers falling ahead
for(j = 0; j < MAX-1-i; j++) {
printf("Items compared: [ %d, %d ] ", list[j],list[j+1]);](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-256-320.jpg)
![Data Structures & Algorithms
248
// check if next number is lesser than current no
// swap the numbers.
// (Bubble up the highest number)
if(list[j] > list[j+1]) {
temp = list[j];
list[j] = list[j+1];
list[j+1] = temp;
swapped = true;
printf(" => swapped [%d, %d]n",list[j],list[j+1]);
}else {
printf(" => not swappedn");
}
}
// if no number was swapped that means
// array is sorted now, break the loop.
if(!swapped) {
break;
}
printf("Iteration %d#: ",(i+1));
display();
}
}
main(){
printf("Input Array: ");
display();
printf("n");
bubbleSort();
printf("nOutput Array: ");
display();
}](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-257-320.jpg)
![Data Structures & Algorithms
249
If we compile and run the above program, it will produce the following result −
Input Array: [1 8 4 6 0 3 5 2 7 9 ]
Items compared: [ 1, 8 ] => not swapped
Items compared: [ 8, 4 ] => swapped [4, 8]
Items compared: [ 8, 6 ] => swapped [6, 8]
Items compared: [ 8, 0 ] => swapped [0, 8]
Items compared: [ 8, 3 ] => swapped [3, 8]
Items compared: [ 8, 5 ] => swapped [5, 8]
Items compared: [ 8, 2 ] => swapped [2, 8]
Items compared: [ 8, 7 ] => swapped [7, 8]
Items compared: [ 8, 9 ] => not swapped
Iteration 1#: [1 4 6 0 3 5 2 7 8 9 ]
Items compared: [ 1, 4 ] => not swapped
Items compared: [ 4, 6 ] => not swapped
Items compared: [ 6, 0 ] => swapped [0, 6]
Items compared: [ 6, 3 ] => swapped [3, 6]
Items compared: [ 6, 5 ] => swapped [5, 6]
Items compared: [ 6, 2 ] => swapped [2, 6]
Items compared: [ 6, 7 ] => not swapped
Items compared: [ 7, 8 ] => not swapped
Iteration 2#: [1 4 0 3 5 2 6 7 8 9 ]
Items compared: [ 1, 4 ] => not swapped
Items compared: [ 4, 0 ] => swapped [0, 4]
Items compared: [ 4, 3 ] => swapped [3, 4]
Items compared: [ 4, 5 ] => not swapped
Items compared: [ 5, 2 ] => swapped [2, 5]
Items compared: [ 5, 6 ] => not swapped
Items compared: [ 6, 7 ] => not swapped
Iteration 3#: [1 0 3 4 2 5 6 7 8 9 ]
Items compared: [ 1, 0 ] => swapped [0, 1]
Items compared: [ 1, 3 ] => not swapped
Items compared: [ 3, 4 ] => not swapped
Items compared: [ 4, 2 ] => swapped [2, 4]
Items compared: [ 4, 5 ] => not swapped
Items compared: [ 5, 6 ] => not swapped](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-258-320.jpg)
![Data Structures & Algorithms
250
Iteration 4#: [0 1 3 2 4 5 6 7 8 9 ]
Items compared: [ 0, 1 ] => not swapped
Items compared: [ 1, 3 ] => not swapped
Items compared: [ 3, 2 ] => swapped [2, 3]
Items compared: [ 3, 4 ] => not swapped
Items compared: [ 4, 5 ] => not swapped
Iteration 5#: [0 1 2 3 4 5 6 7 8 9 ]
Items compared: [ 0, 1 ] => not swapped
Items compared: [ 1, 2 ] => not swapped
Items compared: [ 2, 3 ] => not swapped
Items compared: [ 3, 4 ] => not swapped
Output Array: [0 1 2 3 4 5 6 7 8 9 ]](https://image.slidesharecdn.com/learndatastructuresalgorithmstutorial-180620080749/85/Learn-data-structures-algorithms-tutorial-259-320.jpg)



































































![Présentation_gestion[1] [Autosaved].pptx](https://cdn.slidesharecdn.com/ss_thumbnails/prsentationgestion1autosaved-250608153959-37fabfd3-thumbnail.jpg?width=560&fit=bounds)




