lecture8-final.pdf ( analysis and design of algorithm)
- 1. CSE 202: Design and Analysis of Algorithms Lecture 8 Instructor: Kamalika Chaudhuri
- 2. Last Class: Max Flow Problem An s-t flow is a function f: E R such that: - 0 <= f(e) <= c(e), for all edges e - flow into node v = flow out of node v, for all nodes v except s and t, Size of flow f = Total flow out of s = total flow into t → s v t u 2/2 1/1 1/3 2/5 1/2 Size of f = 3 � e into v f(e) = � e out of v f(e) The Max Flow Problem: Given directed graph G=(V,E), source s, sink t, edge capacities c(e), find an s-t flow of maximum size
- 3. Last Class: Flows and Cuts s v t u 2/2 1/1 1/3 2/5 1/2 The Max Flow Problem: Given directed graph G=(V,E), source s, sink t, edge capacities c(e), find an s-t flow of maximum size An s-t Cut partitions nodes into groups = (L, R) s.t. s in L, t in R Capacity of a cut (L, R) = Property: For any flow f, any s-t cut (L, R), size(f) <= capacity(L, R) � (u,v)∈E,u∈L,v∈R c(u, v) Thus, a Min Cut is a certificate of optimality for a flow Max-Flow <= Min-Cut Cuts Flows R* L* Size of f = 3 � (u,v)∈E,u∈L,v∈R f(u, v) − � (v,u)∈E,u∈L,v∈R f(v, u) Flow across (L,R) =
- 4. Gf = (V, Ef) where Ef E U ER For any (u,v) in E or ER, cf(u,v) = c(u,v) – f(u,v) + f(v,u) [ignore edges with zero cf: don’t put them in Ef] ⊆ Last Class: Ford-Fulkerson Algorithm 1: Construct a residual graph Gf (“what’s left to take?”) s a b t 1 1 1 1 1 s a b t 1 1 1 Example G: f: Gf : s a b t 1 1 1 1 1 2: Find a path from s to t in Gf 3: Increase flow along this path, as much as possible FF Algorithm: Start with zero flow Repeat: Find a path from s to t along which flow can be increased Increase the flow along that path In any iteration, we have some flow f and we are trying to improve it. How to do this?
- 5. FF algorithm gives us a valid flow. But is it the maximum possible flow? Consider final residual graph Gf = (V, Ef) Let L = nodes reachable from s in Gf and let R = rest of nodes =V – L So s L and t R � (u,v)∈E,u∈L,v∈R c(u, v) Analysis: Correctness s L t R Edges from L to R must be at full capacity Edges from R to L must be empty Therefore, flow across cut (L,R) is Thus, size(f) = capacity(L,R) Recall: for any flow and any cut, size(flow) <= capacity(cut) Therefore f is the max flow and (L,R) is the min cut! ∈ ∈ Thus, Max Flow = Min Cut Cuts Flows x y z w
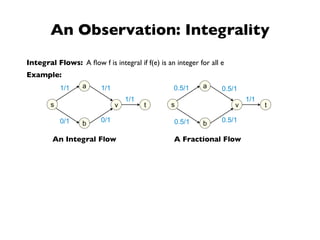
- 6. An Observation: Integrality Integral Flows: A flow f is integral if f(e) is an integer for all e Example: s a b v 1/1 0/1 1/1 0/1 t 1/1 An Integral Flow s a b v 0.5/1 0.5/1 t 1/1 0.5/1 0.5/1 A Fractional Flow
- 7. Property: If all edge capacities are integers, then, there is a max flow f which is integral. An Observation: Integrality Integral Flows: A flow f is integral if f(e) is an integer for all e Example: s a b v 1/1 0/1 1/1 0/1 t 1/1 An Integral Flow s a b v 0.5/1 0.5/1 t 1/1 0.5/1 0.5/1 A Fractional Flow
- 8. Property: If all edge capacities are integers, then, there is a max flow f which is integral. An Observation: Integrality Integral Flows: A flow f is integral if f(e) is an integer for all e Example: s a b v 1/1 0/1 1/1 0/1 t 1/1 An Integral Flow s a b v 0.5/1 0.5/1 t 1/1 0.5/1 0.5/1 A Fractional Flow Proof: If the edge capacities are integers, then, the FF algorithm always finds an integral flow The FF algorithm also always finds a max flow.
- 9. Property: If all edge capacities are integers, then, there is a max flow f which is integral. An Observation: Integrality Integral Flows: A flow f is integral if f(e) is an integer for all e Example: s a b v 1/1 0/1 1/1 0/1 t 1/1 An Integral Flow s a b v 0.5/1 0.5/1 t 1/1 0.5/1 0.5/1 A Fractional Flow Note: All max flows are not necessarily integral flows! Proof: If the edge capacities are integers, then, the FF algorithm always finds an integral flow The FF algorithm also always finds a max flow.
- 10. Analysis: efficiency A hillclimbing procedure Flow size: 0 max flow How many iterations are needed to reach the maximum flow? Example: Each iteration is fast (O(|E|) time). s a b t 106 106 106 106 1 FF Algorithm: Start with zero flow Repeat: Find a path from s to t along which flow can be increased Increase the flow along that path s a b t 1 1 1 s a b t 1 1 1 #iterations can be Max Capacity
- 11. Analysis: efficiency A hillclimbing procedure Flow size: 0 max flow How many iterations are needed to reach the maximum flow? Example: Each iteration is fast (O(|E|) time). s a b t 106 106 106 106 1 FF Algorithm: Start with zero flow Repeat: Find a path from s to t along which flow can be increased Increase the flow along that path #iterations can be Max Capacity (with integer capacities)
- 12. How to improve the efficiency? • Ford-Fulkerson Style Algorithms: • Edmonds Karp • Capacity Scaling • Preflow-Push
- 13. Edmonds Karp Bad Example: FF Algorithm: Start with zero flow Repeat: Find a path from s to t along which flow can be increased Increase the flow along that path Bad Path Sequence: (s, a, b, t), (s, b, a, t), (s, a, b, t),... s a b t 106 106 106 106 1
- 14. Edmonds Karp EK Path Selection: Find the shortest path along which flow can be increased (shortest path = shortest in terms of #edges) Bad Example: FF Algorithm: Start with zero flow Repeat: Find a path from s to t along which flow can be increased Increase the flow along that path Bad Path Sequence: (s, a, b, t), (s, b, a, t), (s, a, b, t),... s a b t 106 106 106 106 1
- 15. Edmonds Karp EK Algorithm: Start with zero flow Repeat: Find the shortest path from s to t along which flow can be increased Increase the flow along that path s a b t 106 106 Iteration 1 f Bad Example for FF: s a b t 106 106 106 106 1
- 16. Edmonds Karp EK Algorithm: Start with zero flow Repeat: Find the shortest path from s to t along which flow can be increased Increase the flow along that path s a b t 106 106 s a b t 106 106 106 106 1 Iteration 1 f Gf Bad Example for FF: s a b t 106 106 106 106 1
- 17. Edmonds Karp EK Algorithm: Start with zero flow Repeat: Find the shortest path from s to t along which flow can be increased Increase the flow along that path s a b t 106 106 s a b t 106 106 s a b t 106 106 106 106 1 Iteration 1 f Iteration 2 Gf f Bad Example for FF: s a b t 106 106 106 106 1
- 18. Edmonds Karp EK Algorithm: Start with zero flow Repeat: Find the shortest path from s to t along which flow can be increased Increase the flow along that path s a b t 106 106 s a b t 106 106 s a b t 106 106 106 106 1 s a b t 106 106 106 106 1 Iteration 1 f Iteration 2 Gf f Gf Bad Example for FF: s a b t 106 106 106 106 1
- 19. Edmonds Karp EK Path Selection: Find the shortest path along which flow can be increased (shortest path = shortest in terms of #edges) It can be shown that this requires only O(|V||E|) iterations (Proof not in this class) FF Algorithm: Start with zero flow Repeat: Find a path from s to t along which flow can be increased Increase the flow along that path Bad Path Sequence: (s, a, b, t), (s, b, a, t), (s, a, b, t),... Bad Example for FF: s a b t 106 106 106 106 1
- 20. Edmonds Karp EK Path Selection: Find the shortest path along which flow can be increased (shortest path = shortest in terms of #edges) It can be shown that this requires only O(|V||E|) iterations (Proof not in this class) Running Time: O(|V| |E|2) FF Algorithm: Start with zero flow Repeat: Find a path from s to t along which flow can be increased Increase the flow along that path Bad Path Sequence: (s, a, b, t), (s, b, a, t), (s, a, b, t),... Bad Example for FF: s a b t 106 106 106 106 1
- 21. How to improve the efficiency? • Ford-Fulkerson Style Algorithms: • Edmonds Karp • Capacity Scaling • Preflow-Push
- 22. Capacity Scaling Capacity Scaling: Find paths of high capacity first between s and t Bad Example: FF Algorithm: Start with zero flow Repeat: Find a path from s to t along which flow can be increased Increase the flow along that path Bad Path Sequence: (s, a, b, t), (s, b, a, t), (s, a, b, t),... s a b t 106 106 106 106 1
- 23. Capacity Scaling Cmax = max capacity edge. Start with D = Cmax Start with zero flow While D >= 1, repeat: Gf(D) = D-residual graph While there is a path from s to t in Gf(D) along which flow can be increased Increase flow along that path Update Gf(D) D = D/2 D-Residual Graph: Subgraph of residual graph with only edges with capacity >= D Example: s a b t 106 106 106 106 1 G s a b t 106 106 106 106 Gf(10) For f = 0
- 24. Capacity Scaling: Correctness Cmax = max capacity edge. Start with D = Cmax Start with zero flow While D >= 1, repeat: Gf(D) = D-residual graph While there is a path from s to t in Gf(D) along which flow can be increased Increase flow along that path Update Gf(D) D = D/2 D-Residual Graph: Subgraph of residual graph with only edges with capacity >= D Property: If all edge capacities are integers, algorithm outputs a max flow Proof: At D=1, Gf(D) = Gf. So on termination, Gf(D) has no more paths from s to t
- 25. Capacity Scaling: Running Time Cmax = max capacity edge. Start with D = Cmax Start with zero flow While D >= 1, repeat: Gf(D) = D-residual graph While there is a path from s to t in Gf(D) along which flow can be increased Increase flow along that path Update Gf(D) D = D/2 D-Residual Graph: Subgraph of residual graph with only edges with capacity >= D Property 1: While loop 1 is executed 1 + log2 Cmax times 1 2 D scaling phase
- 26. Capacity Scaling: Running Time Cmax = max capacity edge. Start with D = Cmax Start with zero flow While D >= 1, repeat: Gf(D) = D-residual graph While there is a path from s to t in Gf(D) along which flow can be increased Increase flow along that path Update Gf(D) D = D/2 D-Residual Graph: Subgraph of residual graph with only edges with capacity >= D Property 1: While loop 1 is executed 1 + log2 Cmax times 1 2 Property 2: At the end of a D-scaling phase, size(max flow) <= size(current flow) + D|E| D scaling phase max flow curr- ent D|E|
- 27. Capacity Scaling: Running Time Cmax = max capacity edge. Start with D = Cmax Start with zero flow While D >= 1, repeat: Gf(D) = D-residual graph While there is a path from s to t in Gf(D) along which flow can be increased Increase flow along that path Update Gf(D) D = D/2 D-Residual Graph: Subgraph of residual graph with only edges with capacity >= D Property 1: While loop 1 is executed 1 + log2 Cmax times 1 2 D scaling phase Proof: Let L = nodes reachable from s in Gf(D) and let R = rest of nodes =V – L L s R t Property 2: At the end of a D-scaling phase, size(max flow) <= size(current flow) + D|E| max flow curr- ent D|E|
- 28. Capacity Scaling: Running Time Cmax = max capacity edge. Start with D = Cmax Start with zero flow While D >= 1, repeat: Gf(D) = D-residual graph While there is a path from s to t in Gf(D) along which flow can be increased Increase flow along that path Update Gf(D) D = D/2 D-Residual Graph: Subgraph of residual graph with only edges with capacity >= D Property 1: While loop 1 is executed 1 + log2 Cmax times 1 2 D scaling phase Proof: Let L = nodes reachable from s in Gf(D) and let R = rest of nodes =V – L L s R t #edges in Gf(D) in the (L, R) cut = 0 Property 2: At the end of a D-scaling phase, size(max flow) <= size(current flow) + D|E| max flow curr- ent D|E|
- 29. Capacity Scaling: Running Time Cmax = max capacity edge. Start with D = Cmax Start with zero flow While D >= 1, repeat: Gf(D) = D-residual graph While there is a path from s to t in Gf(D) along which flow can be increased Increase flow along that path Update Gf(D) D = D/2 D-Residual Graph: Subgraph of residual graph with only edges with capacity >= D Property 1: While loop 1 is executed 1 + log2 Cmax times 1 2 D scaling phase Proof: Let L = nodes reachable from s in Gf(D) and let R = rest of nodes =V – L L s R t #edges in Gf(D) in the (L, R) cut = 0 #edges in Gf in the (L,R) cut <= |E| Property 2: At the end of a D-scaling phase, size(max flow) <= size(current flow) + D|E| max flow curr- ent D|E|
- 30. Capacity Scaling: Running Time Cmax = max capacity edge. Start with D = Cmax Start with zero flow While D >= 1, repeat: Gf(D) = D-residual graph While there is a path from s to t in Gf(D) along which flow can be increased Increase flow along that path Update Gf(D) D = D/2 D-Residual Graph: Subgraph of residual graph with only edges with capacity >= D Property 1: While loop 1 is executed 1 + log2 Cmax times 1 2 D scaling phase Proof: Let L = nodes reachable from s in Gf(D) and let R = rest of nodes =V – L L s R t #edges in Gf(D) in the (L, R) cut = 0 #edges in Gf in the (L,R) cut <= |E| Capacity of each such edge < D Property 2: At the end of a D-scaling phase, size(max flow) <= size(current flow) + D|E| max flow curr- ent D|E|
- 31. Capacity Scaling: Running Time Cmax = max capacity edge. Start with D = Cmax Start with zero flow While D >= 1, repeat: Gf(D) = D-residual graph While there is a path from s to t in Gf(D) along which flow can be increased Increase flow along that path Update Gf(D) D = D/2 D-Residual Graph: Subgraph of residual graph with only edges with capacity >= D Property 1: While loop 1 is executed 1 + log2 Cmax times 1 2 D scaling phase Proof: Let L = nodes reachable from s in Gf(D) and let R = rest of nodes =V – L L s R t #edges in Gf(D) in the (L, R) cut = 0 #edges in Gf in the (L,R) cut <= |E| Capacity of each such edge < D Thus, size(max flow) <= capacity(L,R) <= size(f) + D|E| Property 2: At the end of a D-scaling phase, size(max flow) <= size(current flow) + D|E| max flow curr- ent D|E|
- 32. Capacity Scaling: Running Time Cmax = max capacity edge. Start with D = Cmax Start with zero flow While D >= 1, repeat: Gf(D) = D-residual graph While there is a path from s to t in Gf(D) along which flow can be increased Increase flow along that path Update Gf(D) D = D/2 D-Residual Graph: Subgraph of residual graph with only edges with capacity >= D Property 1: While loop 1 is executed 1 + log2 Cmax times D scaling phase Property 3: For any D, #iterations of loop 2 in the D-scaling phase <= 2|E| 1 2 Property 2: At the end of a D-scaling phase, size(max flow) <= size(current flow) + D|E|
- 33. Capacity Scaling: Running Time Cmax = max capacity edge. Start with D = Cmax Start with zero flow While D >= 1, repeat: Gf(D) = D-residual graph While there is a path from s to t in Gf(D) along which flow can be increased Increase flow along that path Update Gf(D) D = D/2 D scaling phase Proof: After previous (2D-scaling) phase, size(max flow) <= size(current flow) + 2D|E| 1 2 D-Residual Graph: Subgraph of residual graph with only edges with capacity >= D Property 1: While loop 1 is executed 1 + log2 Cmax times Property 3: For any D, #iterations of loop 2 in the D-scaling phase <= 2|E| Property 2: At the end of a D-scaling phase, size(max flow) <= size(current flow) + D|E|
- 34. Capacity Scaling: Running Time Cmax = max capacity edge. Start with D = Cmax Start with zero flow While D >= 1, repeat: Gf(D) = D-residual graph While there is a path from s to t in Gf(D) along which flow can be increased Increase flow along that path Update Gf(D) D = D/2 D scaling phase Proof: After previous (2D-scaling) phase, size(max flow) <= size(current flow) + 2D|E| Each iteration of loop 2 increases flow size by at least D 1 2 D-Residual Graph: Subgraph of residual graph with only edges with capacity >= D Property 1: While loop 1 is executed 1 + log2 Cmax times Property 3: For any D, #iterations of loop 2 in the D-scaling phase <= 2|E| Property 2: At the end of a D-scaling phase, size(max flow) <= size(current flow) + D|E|
- 35. Capacity Scaling: Running Time Cmax = max capacity edge. Start with D = Cmax Start with zero flow While D >= 1, repeat: Gf(D) = D-residual graph While there is a path from s to t in Gf(D) along which flow can be increased Increase flow along that path Update Gf(D) D = D/2 D scaling phase Proof: After previous (2D-scaling) phase, size(max flow) <= size(current flow) + 2D|E| Each iteration of loop 2 increases flow size by at least D Therefore, at most 2|E| iterations in the D-scaling phase 1 2 D-Residual Graph: Subgraph of residual graph with only edges with capacity >= D Property 1: While loop 1 is executed 1 + log2 Cmax times Property 3: For any D, #iterations of loop 2 in the D-scaling phase <= 2|E| Property 2: At the end of a D-scaling phase, size(max flow) <= size(current flow) + D|E|
- 36. Capacity Scaling: Running Time Cmax = max capacity edge. Start with D = Cmax Start with zero flow While D >= 1, repeat: Gf(D) = D-residual graph While there is a path from s to t in Gf(D) along which flow can be increased Increase flow along that path Update Gf(D) D = D/2 D scaling phase 1 2 D-Residual Graph: Subgraph of residual graph with only edges with capacity >= D Property 1: While loop 1 is executed 1 + log2 Cmax times Property 3: For any D, #iterations of loop 2 in the D-scaling phase <= 2|E| Property 2: At the end of a D-scaling phase, size(max flow) <= size(current flow) + D|E| Total Running Time: O(|E|2(1 + log2 Cmax)) ( Recall:Time to find a flow path in a residual graph = O(|E|) )
- 37. How to improve the efficiency? • Ford-Fulkerson Style Algorithms: • Edmonds Karp • Capacity Scaling • Preflow-Push
- 38. Preflow-Push Main Idea: - Each node has a label, which is a potential - Route flow from high to low potential v w Labels Idea: Route flow along blue edges
- 39. Preflows � e into v f(e) − � e out of v f(e) ≥ 0 Preflow: A function f: E R is a preflow if: 1. Capacity Constraints: 0 <= f(e) <= c(e) 2. Instead of conservation constraints: → Excess(v) = � e into v f(e) − � e out of v f(e) s a b t 1 1 1 1 1 Example G s a b t 0 0 1 1 0 f excess = 1 excess = 1
- 40. Preflow-Push: Two Operations v w l � e into v f(e) − � e out of v f(e) ≥ 0 Preflow: A function f: E R is a preflow if: 1. Capacity Constraints: 0 <= f(e) <= c(e) 2. Instead of conservation constraints: → Excess(v) = � e into v f(e) − � e out of v f(e) Labeling h assigns a non-negative integer label h(v) to all v inV Push(v, w): Applies if excess(v) > 0, h(w) < h(v), (v, w) in Ef q = min(excess(v), cf(v, w)) Add q to f(v, w) Relabel(v): Applies if excess(v) > 0, for all w s.t (v, w) in Ef, h(w) >= h(v) Increase l(v) by 1
- 41. Pre-Flow Push: The Algorithm Start with labeling: h(s) = n, h(t) = 0, h(v) = 0, for all other v Start with preflow f: f(e) = c(e) for e = (s, v), f(e) = 0, for all other edges e While there is a node (other than t) with positive excess Pick a node v with excess(v) > 0 If there is an edge (v, w) in Ef such that push(v, w) can be applied Push(v, w) Else Relabel(v) Push(v, w): Applies if excess(v) > 0, h(w) < h(v), (v, w) in Ef q = min(excess(v), cf(v, w)) Add q to f(v, w) Relabel(v): Applies if excess(v) > 0, for all w s.t (v, w) in Ef, h(w) >= h(v) Increase h(v) by 1



![Gf = (V, Ef) where Ef E U ER
For any (u,v) in E or ER,
cf(u,v) = c(u,v) – f(u,v) + f(v,u)
[ignore edges with zero cf: don’t put them in Ef]
⊆
Last Class: Ford-Fulkerson Algorithm
1: Construct a residual graph Gf (“what’s left to take?”)
s
a
b
t
1
1
1
1
1
s
a
b
t
1
1
1
Example
G:
f:
Gf :
s
a
b
t
1
1
1
1
1
2: Find a path from s to t in Gf
3: Increase flow along this path, as much as possible
FF Algorithm: Start with zero flow
Repeat:
Find a path from s to t along which flow
can be increased
Increase the flow along that path
In any iteration, we have some flow f and we
are trying to improve it. How to do this?](https://image.slidesharecdn.com/lecture8-final-240612091041-ca98a387/85/lecture8-final-pdf-analysis-and-design-of-algorithm-4-320.jpg)