M.Tech Thesis on Simulation and Hardware Implementation of NLMS algorithm on TMS320C6713 Digital Signal Processor
- 1. Simulation and Hardware Implementation of NLMS algorithm on TMS320C6713 Digital Signal Processor A Dissertation submitted in partial fulfilment for the award of the Degree of Master of Technology in Department of Electronics & Communication Engineering (with specialization in Digital Communication) Supervisor Submitted By: S.K. Agrawal Raj Kumar Thenua Associate Professor Enrolment No.: 07E2SODCM30P611 Department of Electronics & Communication Engineering Sobhasaria Engineering College, Sikar Rajasthan Technical University April 2011
- 2. Candidate’s Declaration I hereby declare that the work, which is being presented in the Dissertation, entitled “Simulation and Hardware Implementation of NLMS algorithm on TMS320C6713 Digital Signal Processor” in partial fulfilment for the award of Degree of “Master of Technology” in Deptt. of Electronics & Communication Engineering with specialization in Digital Communication, and submitted to the Department of Electronics & Communication Engineering, Sobhasaria Engineering College Sikar, Rajasthan Technical University is a record of my own investigations carried under the Guidance of Shri Surendra Kumar Agrawal, Department of Electronics & Communication Engineering, , Sobhasaria Engineering College Sikar, Rajasthan. I have not submitted the matter presented in this Dissertation anywhere for the award of any other Degree. (Raj Kumar Thenua) Digital Communication Enrolment No.: 07E2SODCM30P611 Sobhasaria Engineering College Sikar Counter Signed by Name(s) of Supervisor(s) (S.K. Agrawal) ii
- 3. ACKNOWLEDGEMENT First of all, I would like to express my profound gratitude to my dissertation guide, Mr. S.K. Agrawal (Head of the Department), for his outstanding guidance and support during my dissertation work. I benefited greatly from working under his guidance. His encouragement, motivation and support have been invaluable throughout my studies at Sobhasaria Engineering College, Sikar. I would like to thank Mohd. Sabir Khan (M.Tech coordinator) for his excellent guidance and kind co-operation during the entire study at Sobhasaria Engineering College, Sikar. I would also like to thank all the faculty members of ECE department who have co-operated and encouraged during the study course. I would also like to thank all the staff (technical and non-technical) and librarians of Sobhasaria Engineering College, Sikar who have directly or indirectly helped during the course of my study. Finally, I would like to thank my family & friends for their constant love and support and for providing me with the opportunity and the encouragement to pursue my goals. Raj Kumar Thenua iii
- 4. CONTENTS Candidate’s Declaration ii Acknowledgement iii Contents iv-vi List of Tables vii List of Figures viii-x List of Abbreviations xi-xii List of Symbols xiii ABSTRACT 1 CHAPTER 1: INTRODUCTION 2 1.1 Overview 2 1.2 Motivation 3 1.3 Scope of the work 4 1.4 Objectives of the thesis 5 1.5 Organization of the thesis 5 CHAPTER 2: LITERATURE SURVEY 7 CHAPTER 3: ADAPTIVE FILTERS 12 3.1 Introduction 12 3.1.1 Adaptive Filter Configuration 13 3.1.2 Adaptive Noise Canceller (ANC) 16 Approaches to Adaptive filtering Algorithms 19 3.2.1 Least Mean Square (LMS) Algorithm 20 3.2 3.2.1.1 Derivation of the LMS Algorithm 20 3.2.1.2 Implementation of the LMS Algorithm 21 3.2.2 Normalized Least Mean Square (NLMS) Algorithm 22 3.2.2.1 Derivation of the NLMS Algorithm 23 3.2.2.2 Implementation of the NLMS Algorithm 24 3.2.3 Recursive Least Square (RLS) Algorithm iv 24
- 5. 3.2.3.1 Derivation of the RLS Algorithm 3.2.3.2 Implementation of the RLS Algorithm 3.3 25 27 Adaptive filtering using MATLAB 28 CHAPTER 4: SIMULINK MODEL DESIGN FOR HARDWARE IMPLEMENTATION 31 4.1 Introduction to Simulink 31 4.2 Model design 32 4.2.1 Common Blocks used in Building Model 32 4.2.1.1 C6713 DSK ADC Block 32 4.2.1.2 C6713 DSK DAC Block 33 4.2.1.3 C6713 DSK Target Preferences Block 33 4.2.1.4 C6713 DSK Reset Block 33 4.2.1.5 NLMS Filter Block 34 4.2.1.6 C6713 DSK LED Block 34 4.2.1.7 C6713 DSK DIP Switch Block 34 4.2.2 Building the model Model Reconfiguration 37 4.3.1 The ADC Setting 38 4.3.2 The DAC Settings 39 4.3.3 Setting the NLMS Filter Parameters 40 4.3.4 Setting the Delay Parameters 41 4.3.5 DIP Switch Settings 41 4.3.6 Setting the Constant Value 42 4.3.7 Setting the Constant Data Type 43 4.3.8 Setting the Relational Operator Type 43 4.3.9 Setting the Relational Operator Data Type 43 4.3.10 Switch Setting 4.3 34 44 CHAPTER 5: REAL TIME IMPLEMENTATION ON DSP PROCESSOR 45 5.1 Introduction to Digital Signal Processor (TMS320C6713) 45 5.1.1 Central Processing Unit Architecture 48 5.1.2 General purpose registers overview 49 v
- 6. 5.1.3 Interrupts 49 5.1.4 Audio Interface Codec 50 5.1.5 DSP/BIOS & RTDX 52 5.2 Code Composer Studio as Integrated Development Environment 54 5.3 MATLAB interfacing with CCS and DSP Processor 58 5.4 Real-time experimental Setup using DSP Processor 58 CHAPTER 6: RESULTS AND DISCUSSION 63 6.1 MATLAB simulation results for Adaptive Algorithms 63 6.1.1 LMS Algorithm Simulation Results 64 6.1.2 NLMS Algorithm Simulation Results 66 6.1.3 RLS Algorithm Simulation Results 67 6.1.4 Performance Comparison of Adaptive Algorithms 67 6.2 Hardware Implementation Results using TMS320C6713 Processor 71 6.2.1 Tone Signal Analysis using NLMS Algorithm 71 6.2.1.1 Effect on Filter Performance at Various Frequencies 73 6.2.1.2 Effect on Filter Performance at Various Amplitudes 75 6.2.2 ECG Signal Analysis using NLMS and LMS Algorithms and their 78 Performance Comparison CHAPTER 7: CONCLUSIONS 85 7.1 Conclusion 85 7.2 Future Work 86 REFERENCES 88 APPENDIX-I LIST OF PUBLICATIONS 93 APPENDIX-II MATLAB COMMANDS 94 vi
- 7. LIST OF TABLES Table No. Title Page No. Table 6.1 Mean Squared Error (MSE) Versus Step Size (µ) 65 Table 6.2 Mean Squared Error versus Filter-order (N) 69 Table 6.3 Performance comparison of various adaptive algorithms 70 Table 6.4 Comparison of Various Parameters for Adaptive Algorithms 70 Table 6.5 SNR Improvement versus voltage and frequency 78 Table 6.6 SNR Improvement versus noise level for a Tone Signal 78 Table 6.7 SNR Improvement versus noise variance for an ECG Signal 84 vii
- 8. LIST OF FIGURES Figure No. Title Page No. Fig.3.1 General adaptive filter configuration 14 Fig.3.2 Transversal FIR filter architecture 15 Fig.3.3 Block diagram for Adaptive Noise Canceller 16 Fig.3.4 MATLAB versatility diagram 29 Fig.4.1 Simulink applications 32 Fig.4.2 Adaptive Noise cancellation Simulink model 33 Fig.4.3 Simulink library browser 35 Fig.4.4 Blank new model window 36 Fig.4.5 Model window with ADC block 37 Fig.4.6 Model illustration before connections 38 Fig.4.7 Setting up the ADC for mono microphone input 39 Fig.4.8 Setting the DAC parameters 39 Fig.4.9 Setting the NLMS filter parameters 40 Fig.4.10 Setting the delay unit 41 Fig.4.11 Setting up the DIP switch values 42 Fig.4.12 Setting the constant parameters 42 Fig.4.13 Data type conversion to 16-bit integer 43 Fig.4.14 Changing the output data type 44 Fig.5.1 Block diagram of TMS320C6713 processor 47 Fig.5.2 Physical overview of the TMS320C6713 processor 47 Fig.5.3 Functional block diagram of TMS320C6713 CPU 48 Fig.5.4 Interrupt priority diagram 49 Fig.5.5 Interrupt handling procedure 50 viii
- 9. Figure No. Title Page No. Fig.5.6 Audio connection illustrating control and data signal 51 Fig.5.7 AIC23 codec interface 52 Fig.5.8 DSP BIOS and RTDX 53 Fig.5.9 Code composer studio platform 54 Fig.5.10 Embedded software development 54 Fig.5.11 Typical 67xx efficiency vs. efforts level for different codes 55 Fig.5.12 Code generation 55 Fig.5.13 Cross development environment 56 Fig.5.14 Signal flow during processing 56 Fig.5.15 Real-time analysis and data visualization 57 Fig.5.16 MATLAB interfacing with CCS and TI target processor 58 Fig.5.17 Experimental setup using Texas Instrument processor 59 Fig.5.18 Real-time setup using Texas Instrument processor 59 Fig.5.19 Model building using RTW 60 Fig.5.20 Code generation using RTDX link 60 Fig.5.21 Target processor in running status 61 Fig.5.22 (a) Switch at Position 0 62 Fig.5.22 (b) Switch at position 1 for NLMS noise reduction 62 Fig.6.1(a) Clean tone(sinusoidal) signal s(n) 63 Fig.6.1(b) Noise signal x(n) 63 Fig.6.1(c) Delayed noise signal x1(n) 64 Fig.6.1(d) Desired signal d(n) 64 Fig.6.2 MATLAB simulation for LMS algorithm; N=19, step size=0.001 64 Fig.6.3 MATLAB simulation for NLMS algorithm; N=19, step size=0.001 66 ix
- 10. Figure No. Title Page No. Fig.6.4 MATLAB simulation for RLS algorithm; N=19, λ =1 67 Fig.6.5 MSE versus step-size (µ) for LMS algorithm 67 Fig.6.6 MSE versus filter order (N) 68 Fig.6.7 Clean tone signal of 1 kHz 72 Fig.6.8 Noise corrupted tone signal 72 Fig.6.9 Filtered tone signal 73 Fig.6.10 Time delay in filtered signal 73 Fig.6.11(a) Filtered output signal at 2 kHz frequency 74 Fig.6.11(b) Filtered output signal at 3 kHz frequency 74 Fig.6.11(c) Filtered output signal at 4 kHz frequency 75 Fig.6.11(d) Filtered output signal at 5 kHz frequency 75 Fig.6.12(a) Filtered output signal at 3V 76 Fig.6.12(b) Filtered output signal at 4V 76 Fig.6.12(c) Filtered output signal at 5V 77 Fig.6.13 Filtered signal at high noise 77 Fig.6.14 ECG waveform 79 Fig.6.15 Clean ECG signal 80 Fig.6.16(a) NLMS filtered output for low level noisy ECG signal 81 Fig.6.16(b) LMS filtered output for low level noisy ECG signal 81 Fig.6.17(a) NLMS filtered output for medium level noisy ECG signal 82 Fig.6.17(b) LMS filtered output for medium level noisy ECG signal 82 Fig.6.18(a) NLMS filtered output for high level noisy ECG signal 83 Fig.6.18(b) LMS filtered output for high level noisy ECG signal 83 x
- 11. LIST OF ABBREBIATIONS ANC Adaptive Noise Cancellation API Application Program Interface AWGN Additive White Gaussian Noise BSL Board Support Library BIOS Basic Input Output System CSL Chip Support Library CCS Code Composer Studio CODEC Coder Decoder COFF Common Object File Format COM Component Object Model CPLD Complex Programmable Logic Device CSV Comma Separated Value DIP Dual Inline Package DSK Digital signal processor Starter Kit DSO Digital Storage Oscilloscope DSP Digital Signal Processor ECG Electrocardiogram EDMA Enhanced Direct Memory Access EMIF External Memory Interface FIR Finite Impulse Response FPGA Field Programmable Gate Array FTRLS Fast Transversal Recursive Least Square GEL General Extension Language GPIO General Purpose Input Output GUI Graphical User Interface HPI Host Port Interface IDE Integrated Development Environment IIR Infinite Impulse Response JTAG Joint Text Action Group LMS Least Mean Square xi
- 12. LSE Least Square Error MA Moving Average McBSP Multichannel Buffered Serial Port McASP Multichannel Audio Serial Port MSE Mean Square Error MMSE Minimum Mean Square Error NLMS Normalized Least Mean Square RLS Recursive Least Squares RTDX Real Time Data Exchange RTW Real Time Workshop SNR Signal to Noise Ratio TI Texas Instrument TVLMS Time Varying Least Mean Squared VLIW Very Long Instruction Word VSLMS Variable Step-size Least Mean Square VSSNLMS Variable Step Size Normalized Least Mean Square xii
- 13. LIST OF SYMBOLS s(n) Source signal x(n) Noise signal or reference signal x1(n) Delayed noise signal w(n) Filter weights d(n) Desired signal y(n) FIR filter output e(n) Error signal + e (n) Advance samples of error signal e (n) Error estimation n Sample number i Iteration N Filter order E Ensemble Z-1 Unit delay wT Transpose of weight vector µ Step size Gradient ξ Cost function x(n) 2 Squared Euclidian norm of the input vector x(n) at iteration n. c Constant term for normalization α NLMS adaption constant λ ~ Λ ( n) Small positive constant k(n) ~ ψ ( n) Gain vector λ ~ Diagonal matrix vector Intermediate matrix θλ Intermediate vector w ( n) Estimation of filter weight vector y ( n) Estimation of FIR filter output xiii
- 14. ABSTRACT Adaptive filtering constitutes one of the core technology in the field of digital signal processing and finds numerous application in the areas of science and technology viz. echo cancellation, channel equalization, adaptive noise cancellation, adaptive beam-forming, biomedical signal processing etc. Noise problems in the environment have gained attention due to the tremendous growth in upcoming technologies which gives spurious outcomes like noisy engines, heavy machinery, high electromagnetic radiation devices and other noise sources. Therefore, the problem of controlling the noise level in the area of signal processing has become the focus of a vast amount of research over the years. In this particular work an attempt has been made to explore the adaptive filtering techniques for noise cancellation using Least Mean Square (LMS), Normalized Least Mean Square (NLMS) and Recursive Least Mean Square (RLS) algorithms. The mentioned algorithms have been simulated in MATLAB and compared for evaluating the best performance in terms of Mean Squared Error (MSE), convergence rate, percentage noise removal, computational complexity and stability. In the specific example of tone signal, LMS has shown low convergence rate, with low computational complexity while RLS has fast convergence rate and shows best performance but at the cost of large computational complexity and memory requirement. However the NLMS provides a trade-off in convergence rate and computational complexity which makes it more suitable for hardware implementation. The hardware implementation of NLMS algorithm is performed for that a simulink model is designed to generate auto C code for the DSP processor. The generated C code is loaded on the DSP processor hardware and the task of real-time noise cancellation is done for the two types of signals i.e. tone signal and biomedical ECG signal. For both types of signals, three noisy signals of different noise levels are used to judge the performance of the designed system. The output results are analysed using Digital Storage Oscilloscope (DSO) in terms of filtered signal SNR improvement. The results have also been compared with the LMS algorithm to prove the superiority of NLMS algorithm. 1
- 15. Chapter-1 INTRODUCTION In the process of transmission of information from the source to receiver, noise from the surroundings automatically gets added to the signal. The noisy signal contains two components, one carries the information of interest i.e. the useful signal; the other consists of random errors or noise which is superimposed on the useful signal. These random errors or noise are unwanted because they diminish the accuracy and precision of the measured signal. Therefore the effective removal or reduction of noise in the field of signal processing is an active area of research. 1.1 Overview The use of adaptive filter [1] is one of the most popular proposed solutions to reduce the signal corruption caused by predictable and unpredictable noise. An adaptive filter has the property of self-modifying its frequency response to change its behavior with time. It allows the filter to adapt to the response as the input signal characteristics change. Due to this capability and the construction flexibility, the adaptive filters have been employed in many different applications like telephonic echo cancellation, radar signal processing, navigation systems, communications, channel equalization, bio-medical & biometric signal processing etc. In the field of adaptive filtering, there are mainly two algorithms that are used to force the filter to adapt its coefficients – Stochastic gradient based algorithm and Recursive Least Square based algorithm. Their implementations and adaptation properties are the determining factors for choice of application. The main requirements and the performance parameters for adaptive filters are the convergence speed and the asymptotic error. The convergence speed is the primary property of an adaptive filter which enables one to measure how quickly the filter is converging to the desired value. It is a major requirement as well as a limiting factor for most of the applications of adaptive filters. The asymptotic error represents the amount of error that the filter introduces at steady state after it has converged to the desired value. The RLS filters due to their computational structure have considerably better properties than the LMS filters both in terms of the 2
- 16. convergence speed and the asymptotic error. The RLS filters which outperform the LMS filters obtain their solution for the weight updated directly from the Mean Square Error (MSE) [2]. However, they are computationally very demanding and also very dependent upon the precision of the input signal. Their computational requirements are significant and imply the use of expensive and power demanding high-speed processors. Also, for the systems lacking the appropriate dynamic range, the adaptation algorithms can become unstable. In this manner to match the computational requirements a DSP processor can be a better substitute. 1.2 Motivation In the field of signal processing there is a significant need of a special class of digital filters known as adaptive filters. Adaptive filters are used commonly in many different configurations for different applications. These filters have various advantages over the standard digital filters. They can adapt their filter coefficients from the environment according to preset rules. The filters are capable of learning from the statistics of current conditions and change their coefficients in order to achieve a certain goal. In order to design a filter prior knowledge of the desired response is required. When such knowledge is not available due to the changing nature of the filter’s requirements, it is impossible to design a standard digital filter. In such situations, adaptive filters are desirable. The algorithms used to perform the adaptation and the configuration of the filter depends directly on the application of the filter. However, the basic computational engine that performs the adaptation of the filter coefficients can be the same for different algorithms and it is based on the statistics of the input signals to the system. The two classes of adaptive filtering algorithms namely Recursive Least Squares (RLS) and Least Mean Squared (LMS) are capable of performing the adaptation of the filter coefficients. When we talk about a real scenario where the information generated from the source side gets contaminated by the noise signal, this situation demands for the adaptive filtering algorithm which provides fast convergence while being numerically stable without incorporating much memory. 3
- 17. Hence, the motivation for the thesis is to search for an adaptive algorithm which has reduced computational complexity, reasonable convergence speed and good stability without degrading the performance of the adaptive filter and then realize the algorithm on an efficient hardware which makes it more practical in real time applications. 1.3 Scope of the Work In numerous application areas, including biomedical engineering, radar & sonar engineering, digital communications etc., the goal is to extract the useful signal corrupted by interferences and noises. In this wok an adaptive noise canceller will be designed that will more effective than available ones. To achieve an effective adaptive noise canceller, the simulation of various adaptive algorithms will be done on MATLAB. The obtained suitable algorithm will be implemented on the TMS320C6713 DSK hardware. The designed system will be tested for the filtering of a noisy ECG signal and tone signal and the system performance will be compared with the early designed available systems. The designed system may be useful for cancelling of interference in ECG signal, periodic interference in audio signal and broad-band interference in the side-lobes of an antenna array. In this work for the simulation, MATLAB version 7.4.0.287(R2007a) is used, though Labview version7 may also be applicable. For the hardware implementation, Texas Instrument (TI) TMS320C6713 digital signal processor is used. However, Field Programmable Gate Array (FPGA) may also be suitable. To assist the hardware implementation Simulink version 6.6 is appropriate to generate C code for the DSP hardware. To communicate with DSP processor, Integrated Development Environment (IDE) software Code Composer Studio V3.1 is essential. Function generator and noise generator or any other audio device can be used as an input source for signal analysis. For the analysis of output data DSO is essentially required however CRO may also be used. Current adaptive noise cancellation models [5], [9], [11] works on relatively low processing speed that is not suitable for real-time signals which results delay in output. In this direction, to increase the processing speed and to improve signal-to-noise ratio, a DSP processor can be useful because it is a fast special purpose microprocessor with a specialized type of architecture and an appropriate instruction set for signal processing. It is also well suited for numerically intensive calculations. 4
- 18. 1.4 Objectives of the Thesis The core of this thesis is to analyze and filter the noisy signals (real-time as well as non-real time) by various adaptive filtering techniques in software as well as in hardware, using MATLAB & DSP processor respectively. The basic objective is to focus on the hardware implementation of adaptive algorithms for filtering so the DSP processor is employed in this work as it can deal more efficiently with real-time as well as non-real time signals. The objectives of the thesis are as follows: (a) To perform the MATLAB simulation of Least Mean Squared (LMS), Normalized Least Mean Squared (NLMS) and Recursive Least Square (RLS) algorithms and to compare their relative performance with a tone signal. (b) Design a simulink model to generate auto C code for the hardware implementation of NLMS and LMS algorithms. (c) Hardware implementation of NLMS and LMS algorithms to perform the analysis of an ECG signal and tone signal. (d) To compare the performance of NLMS and LMS algorithms in terms of SNR improvement for an ECG signal. 1.5 Organization of the Thesis The work emphasizing on the implementation of various adaptive filtering algorithms using MATLAB, Simulink and DSP processor, in this regard the thesis is divided into seven chapters as follows: Chapter-2 deals with the literature survey for the presented work, where so many papers from IEEE and other refereed journals or proceedings are taken which relate the present work with recent research work going on worldwide and assure the consistency of the work. Chapter-3 presents a detailed introduction of adaptive filter theory and various adaptive filtering algorithms with problem definition. 5
- 19. Chapter-4 presents a brief introduction of simulink. An adaptive noise cancellation model is designed for adaptive noise cancellation with the capability of C code generation to implement on DSP processor. Chapter-5 illustrates experimental setup for the real-time implementation of an adaptive noise canceller on a DSK. Therefore a brief introduction of TMS320C6713 processor and code composer studio (CCS) with real-time workshop facility is also presented. Chapter-6 shows the experimental outcomes for the various algorithms. This chapter is divided in two parts, first part shows the MATLAB simulation results for a sinusoidal tone signal and the second part illustrates the real time DSP Processor implementation results for sinusoidal tone signal and ECG signal. The results from DSP processor are analyzed with the help of DSO. Chapter-7 summarizes the work and provides suggestions for future research. 6
- 20. Chapter-2 LITERATURE SURVEY In the last thirty years significant contributions have been made in the field of signal processing. The advances in digital circuit design have been the key technological development that sparked a growing interest in the field of digital signal processing. The resulting digital signal processing systems are attractive due to their low cost, reliability, accuracy, small physical sizes and flexibility. In numerous applications of signal processing, communications and biomedical we face the necessity to remove noise and distortion from the signals. These phenomena are due to time-varying physical processes which are unknown sometimes. One of these situations is during the transmission of a signal from one point to another. The channel which may be of wires, fibers, microwave beam etc., introduces noise and distortion due to the variations of its properties. These variations may be slow or fast. Since most of the time the variations are unknown, so there is a requirement of such type of filters that can work effectively in such unknown environment. The adaptive filter is the right choice that diminishes and sometimes completely eliminates the signal distortion. The most common adaptive filters which are used during the adaption process are the finite impulse response (FIR) types. These are preferable because they are stable, and no special adjustments are needed for their implementation. In adaptive filters, the filter weights are needed to be updated continuously according to certain rules. These rules are presented in form of algorithms. There are mainly two types of algorithms that are used for adaptive filtering. The first is stochastic gradient based algorithm known as Least Mean Squared (LMS) algorithm and second is based on least square estimation which is known as Recursive Least Square (RLS) algorithm. A great deal of research [1]-[5], [14], [15] has been carried out in subsequent years for finding new variant of these algorithms to achieve better performance in noise cancellation applications. Bernard Widrow et. al.[1] in 1975, described the adaptive noise cancelling as an alternative method of estimating signals which are corrupted by additive noise or interference by employing LMS algorithm. The method uses a “primary” input containing the corrupted signal and a “reference” input containing noise correlated in some unknown way with the 7
- 21. primary noise. The reference input is adaptively filtered and subtracted from the primary input to obtain the signal estimate. Widrow [1] focused on the usefulness of the adaptive noise cancellation technique in a variety of practical applications that included the cancelling of various forms of periodic interference in electrocardiography, the cancelling of periodic interference in speech signals, and the cancelling of broad-band interference in the side-lobes of an antenna array. In 1988, Ahmed S. Abutaleb [2] introduced a new principle- Pontryagin minimum principal to reduce the computational time of LMS algorithm. The proposed method reduces the computation time drastically without degrading the accuracy of the system. When compared to the LMS-based widrow [1] model, it was shown to have superior performance. The LMS based algorithms are simple and easy to implement but the convergence speed is slow. Abhishek Tandon et. al.[3] introduced an efficient, low-complexity Normalized least mean squared (NLMS) algorithm for echo cancellation in multiple audio channels. The performance of the proposed algorithm was compared with other adaptive algorithms for acoustic echo cancellation. It was shown that the proposed algorithm has reduced complexity, while providing a good overall performance. In NLMS algorithm, all the filter coefficients are updated for each input sample. Dong Hang et. al.[4] presented a multi-rate algorithm which can dynamically change the update rate of the coefficients of filter by analyzing the actual application environment. When the environment is varying, the rate increases while it decreases when the environment is stable. The results of noise cancellation indicate that the new method has faster convergence speed, low computation complexity, and the same minimum error as the traditional method. Ying He et. al.[5] presented the MATLAB simulation of RLS algorithm and the performance was compared with LMS algorithm. The convergence speed of RLS algorithm is much faster and produces a minimum mean squared error (MSE) among all available LMS based algorithms but at the cost of increased computational complexity which makes its implementation difficult on hardware. Nowadays the availability of high speed digital signal processors has attracted the attention of the research scholars towards the real-time implementation of the available algorithms on the hardware platform. Digital signal processors are fast special-purpose 8
- 22. microprocessors with a specialized type of architecture and an instruction set appropriate for signal processing. The architecture of the digital signal processor is very well suited for numerically intensive calculations. DSP techniques have been very successful because of the development of low-cost software and hardware support. DSP processors are concerned primarily with real-time signal processing. DSP processors exploit the advantages of microprocessors. They are easy to use, flexible, economical and can be reprogrammed easily. The starting of real-time hardware implementation was done by Edgar Andrei [6] initially on the Motorola DSP56307 in 2000. Later in year 2002, Michail D. Galanis et. al.[7] presented a DSP course for real-time systems design and implementation based on the TMS320C6211. This course emphasized the issue of transition from an advanced design and simulation environment like MATLAB to a DSP software environment like Code Composer Studio. Boo-Shik Ryu et. al.[8] implemented and investigated the performance of a noise canceller with DSP processor (TMS320C6713) using the LMS algorithm, NLMS algorithm and VSS-NLMS algorithm. Results showed that the proposed combination of hardware and VSS-NLMS algorithm has not only a faster convergence rate but also lower distortion when compared with the fixed step size LMS algorithm and NLMS algorithm in real time environments. In 2009, J. Gerardo Avalos et. al. [9] have done an implementation of a digital adaptive filter on the digital signal processor TMS320C6713 using a variant of the LMS algorithm which consists of error codification. The speed of convergence is increased and the complexity of design for its implementation in digital adaptive filters is reduced because the resulting codified error is composed of integer values. The LMS algorithm with codified error (ECLMS) was tested in an environmental noise canceller and the results demonstrate an increase in the convergence speed and a reduction of processing time. C.A. Duran et. al. [10] presented an implementation of the LMS, NLMS and other LMS based algorithms on the DSK TMS320C6713 with the intention to compare their performance, analyze their time & frequency behavior along with the processing speed of the algorithms. The objective of the NLMS algorithm is to obtain the best convergence factor considering the input signal power in order to improve the filter convergence time. The 9
- 23. obtained results show that the NLMS has better performance than the LMS. Unfortunately, the computational complexity increases which means more processing time. The work related to real-time implementation so far discussed was implemented on DSP processor by writing either assembly or C program directly in the editor of Code Composer Studio (CCS). The writing of assembly program needs so many efforts therefore only professional person can do this similarly C programming are not simple as far as hardware implementation concerned. There is a simple way to create C code automatically which requires less effort and is more efficient. Presently only few researchers [11]-[13] are aware about this facility which is provided by the MATLAB Version 7.1 and higher versions, using embedded target Real-time Workshop (RTW). Gaurav Saxena et. al. [11] have used this auto code generation facility and presented better results than the conventional C code writing. Gaurav Saxena et. al. [11] discussed the real time implementation of adaptive noise cancellation based on an improved adaptive wiener filter on Texas Instruments TMS320C6713 DSK. Then its performance was compared with the Lee’s adaptive wiener filter. Furthermore, a model based design of adaptive noise cancellation based on LMS filter using simulink was implemented on TI C6713. The auto-code generated by the Real Time Workshop for the simulink model of LMS filter was compared with the ‘C’ implementation of LMS filter on C6713 in terms of code length and computation time. It was found to have a large improvement in computation time but at the cost of increased code length. S.K. Daruwalla et. al. [12] focused on the development and the real time implementation of various audio effects using simulink blocks by employing an audio signal as input. This system has helped the sound engineers to easily configure/capture various audio effects in advance by simply varying the values of predefined simulink blocks. The digital signal processor is used to implement the designs; this broadens the versatility of system by allowing the user to employ the processor for any audio input in real-time. The work is enriched with the real-time concepts of controlling the various audio effects via onboard DIP switches on the C6713 DSK. 10
- 24. In Nov-2009, Yaghoub Mollaei [13] designed an adaptive FIR filter with normalized LMS algorithm to cancel the noise. A simulink model is created and linked to TMS320C6711 digital signal processor through embedded target for C6000 SIMULINK toolbox and realtime workshop to perform hardware adaptive noise cancellation. Three noises with different powers were used to test and judge the system performance in software and hardware. The background noises for speech and music track were eliminated adequately with reasonable rate for all the tested noises. The outcomes of the literature survey can be summarized as follows: The adaptive filters are attractive to work in an unknown environment and are suitable for noise cancellation applications in the field of digital signal processing. To update the adaptive filter weights two types of algorithms, LMS & RLS are used. RLS based algorithms have better performance but at the cost of larger computational complexity therefore very less work [5], [15] is going on in this direction. On the other hand, LMS based algorithms are simple to implement and its few variants like NLMS have comparable performance with RLS algorithm. So a large amount of research [1]-[5] through simulation has been carried out in this regard to improve the performance of LMS based algorithms. Simulation can be carried out on non-real time signals only. Therefore for real-time application there is a need of the hardware implementation of LMS based algorithms. The DSP processor has been found to be a suitable hardware for signal processing applications. Hence, there is a requirement to find out the easiest way for the hardware implementation of adaptive filter algorithms on a particular DSP processor. The use of simulink model [11]-[13] with embedded target and real time workshop has proved to be helpful for the same. Therefore the simulink based hardware implementation of NLMS algorithm for ECG signal analysis can be a good contribution in the field of adaptive filtering. 11
- 25. Chapter-3 ADAPTIVE FILTERS 3.1 Introduction Filtering is a signal processing operation. Its objective is to process a signal in order to manipulate the information contained in the signal. In other words, a filter is a device that maps its input signal to another output signal facilitating the extraction of the desired information contained in the input signal. A digital filter is the one that processes discretetime signals represented in digital format. For time-invariant filters the internal parameters and the structure of the filter are fixed, and if the filter is linear the output signal is a linear function of the input signal. Once the prescribed specifications are given, the design of timeinvariant linear filters entails three basic steps namely; the approximation of the specifications by a rational transfer function, the choice of an appropriate structure defining the algorithm, and the choice of the form of implementation for the algorithm. An adaptive filter [1], [2] is required when either the fixed specifications are unknown or the specifications cannot be satisfied by time-invariant filters. Strictly speaking, an adaptive filter is a nonlinear filter since its characteristics are dependent on the input signal and consequently the homogeneity and additivity conditions are not satisfied. However, if we freeze the filter parameters at a given instant of time, most adaptive filters are linear in the sense that their output signals are linear functions of their input signals. The adaptive filters are time-varying since their parameters are continuously changing in order to meet a performance requirement. In this sense, we can interpret an adaptive filter as a filter that performs the approximation step on-line. Usually, the definition of the performance criterion requires the existence of a reference signal that is usually hidden in the approximation step of fixed-filter design. Adaptive filters are considered nonlinear systems; therefore their behaviour analysis is more complicated than for fixed filters. On the other hand, since the adaptive filters are self designing filters from the practitioner’s point of view, their design can be considered less involved than the digital filters with fixed coefficients. 12
- 26. Adaptive filters work on the principle of minimizing the mean squared difference (or error) between the filter output and a target (or desired) signal. Adaptive filters are used for estimation of non-stationary signals and systems, or in applications where a sample-by sample adaptation of a process and a low processing delay is required. Adaptive filters are used in applications [26]-[29] that involve a combination of three broad signal processing problems: (1) De-noising and channel equalization – filtering a time-varying noisy signal to remove the effect of noise and channel distortions. (2) Trajectory estimation – tracking and prediction of the trajectory of a non stationary signal or parameter observed in noise. (3) System identification – adaptive estimation of the parameters of a time-varying system from a related observation. Adaptive linear filters work on the principle that the desired signal or parameters can be extracted from the input through a filtering or estimation operation. The adaptation of the filter parameters is based on minimizing the mean squared error between the filter output and a target (or desired) signal. The use of the Least Square Estimation (LSE) criterion is equivalent to the principal of orthogonality in which at any discrete time m the estimator is expected to use all the available information such that any estimation error at time m is orthogonal to all the information available up to time m. 3.1.1 Adaptive Filter Configuration The general set up of an adaptive-filtering environment is illustrated in Fig.3.1 [43], where n is the iteration number, x(n) denotes the input signal, y(n) is the adaptive-filter output signal, and d(n) defines the desired signal. The error signal e (n) is calculated as d (n) – y (n). The error signal is then used to form a performance function that is required by the adaptation algorithm in order to determine the appropriate updating of the filter coefficients. The minimization of the objective function implies that the adaptive-filter output signal is matching the desired signal in some sense. At each sampling time, an adaptation algorithm adjusts the filter coefficients w(n) =[w0(n)w1(n)….. wN−1(n)] to minimize the difference between the filter output and a desired or target signal. 13
- 27. d(n) y(n) Adaptive Filter x(n) _ ⊕ e(n) Adaptive Algorithm Fig.3.1. General Adaptive filter configuration The complete specification of an adaptive system, as shown in Fig. 3.1, consists of three things: (a) Input: The type of application is defined by the choice of the signals acquired from the environment to be the input and desired-output signals. The number of different applications in which adaptive techniques are being successfully used has increased enormously during the last two decades. Some examples are echo cancellation, equalization of dispersive channels, system identification, signal enhancement, adaptive beam-forming, noise cancelling and control. (b) Adaptive-filter structure: The adaptive filter can be implemented in a number of different structures or realizations. The choice of the structure can influence the computational complexity (amount of arithmetic operations per iteration) of the process and also the necessary number of iterations to achieve a desired performance level. Basically, there are two major classes of adaptive digital filter realization, distinguished by the form of the impulse response, namely the finite-duration impulse response (FIR) filter and the infinite-duration impulse response (IIR) filters. FIR filters are usually implemented with nonrecursive structures, whereas IIR filters utilize recursive realizations. Adaptive FIR filter realizations: The most widely used adaptive FIR filter structure is the transversal filter, also called tapped delay line, that implements an all-zero transfer function with a canonic direct form realization without feedback. For this realization, the output signal y(n) is a linear combination of the filter coefficients, that 14
- 28. yields a quadratic mean-square error (MSE = E[|e(n)|2]) function with a unique optimal solution. Other alternative adaptive FIR realizations are also used in order to obtain improvements as compared to the transversal filter structure, in terms of computational complexity, speed of convergence and finite word-length properties. Adaptive IIR filter realizations: The most widely used realization of adaptive IIR filters is the canonic direct form realization [42], due to its simple implementation and analysis. However, there are some inherent problems related to recursive adaptive filters which are structure dependent such as pole-stability monitoring requirement and slow speed of convergence. To address these problems, different realizations were proposed attempting to overcome the limitations of the direct form structure. (c) Algorithm: The algorithm is the procedure used to adjust the adaptive filter coefficients in order to minimize a prescribed criterion. The algorithm is determined by defining the search method (or minimization algorithm), the objective function and the nature of error signal. The choice of the algorithm determines several crucial aspects of the overall adaptive process, such as existence of sub-optimal solutions, biased optimal solution and computational complexity. x(n) w0 Z‐1 ⊗ x(n-1) w1 Z-1 Z-1 ⊗ wN-1 ⊕ y(n) ⊕ _ e(n) d(n) + Fig.3.2. Transversal FIR filter architecture 15 x(n-N+1) ⊗
- 29. 3.1.2 Adaptive Noise Canceller (ANC) The goal of adaptive noise cancellation system is to reduce the noise portion and to obtain the uncorrupted desired signal. In order to achieve this task, a reference of the noise signal is needed. That reference is fed to the system, and it is called a reference signal x(n). However, the reference signal is typically not the same signal as the noise portion of the primary signal; it can vary in amplitude, phase or time. Therefore, the reference signal cannot be simply subtracted from the primary signal to obtain the desired portion at the output. Signal Source Noise Source s(n) Primary Input d(n) x1(n) Reference Input x(n) Adaptive Filter + Σ e(n) Output _ y(n) Adaptive Noise Canceller Fig.3.3. Block diagram for Adaptive Noise Canceller Consider the Adaptive Noise Canceller (ANC) shown in Fig.3.3 [1]. The ANC has two inputs: the primary input d(n), which represents the desired signal corrupted with undesired noise and the reference input x(n), which is the undesired noise to be filtered out of the system. The primary input therefore comprises of two portions: - first, the desired signal and the other one is noise signal corrupting the desired portion of the primary signal. The basic idea for the adaptive filter is to predict the amount of noise in the primary signal and then subtract that noise from it. The prediction is based on filtering the reference signal x(n), which contains a solid reference of the noise present in the primary signal. The noise in the reference signal is filtered to compensate for the amplitude, phase and time delay and then subtracted from the primary signal. The filtered noise represented by y(n) is the system’s prediction of the noise portion of the primary signal and is subtracted from desired signal d(n) resulting in a signal called error signal e(n), and it presents the output of the system. Ideally, the resulting error signal should be only the desired portion of the primary signal. 16
- 30. In practice, it is difficult to achieve this, but it is possible to significantly reduce the amount of noise in the primary signal. This is the overall goal of the adaptive filters. This goal is achieved by constantly changing (or adapting) the filter coefficients (weights). The adaptation rules determine their performance and the requirements of the system used to implement the filters. A good example to illustrate the principles of adaptive noise cancellation is the noise removal from the pilot’s microphone in the airplane. Due to the high environmental noise produced by the airplane engine, the pilot’s voice in the microphone gets distorted with a high amount of noise and is very difficult to comprehend. In order to overcome this problem, an adaptive filter can be used. In this particular case, the desired signal is the pilot’s voice. This signal is corrupted with the noise from the airplane’s engine. Here, the pilot’s voice and the engine noise constitute primary signal d(n). Reference signal for the application would be a signal containing only the engine noise, which can be easily obtained from the microphone placed near the engine. This signal would not contain the pilot’s voice, and for this application it is the reference signal x(n). Adaptive filter shown in Fig.3.3 can be used for this application. The filter output y(n) is the system’s estimate of the engine noise as received in the pilot’s microphone. This estimate is subtracted from the primary signal (pilot’s voice plus engine noise), and at the output of the system e(n) should contain only the pilot’s voice without any noise from the airplane’s engine. It is not possible to subtract the engine noise from the pilot’s microphone directly, since the engine noise received in the pilot’s microphone and the engine noise received in the reference microphone are not the same signal. There are differences in amplitude and time delay. Also, these differences are not fixed. They change in time with pilot’s microphone position with respect to the airplane engine, and many other factors. Therefore, designing the fixed filter to perform the task would not obtain the desired results. The application requires adaptive solution. There are many forms of the adaptive filters and their performance depends on the objective set forth in the design. Theoretically, the major goal of any noise cancelling system is to reduce the undesired portion of the primary signal as much as possible, while preserving the integrity of the desired portion of the primary signal. 17
- 31. As noted above, the filter produces estimate of the noise in the primary signal adjusted for magnitude, phase and time delay. This estimate is then subtracted from the noise corrupted primary signal to obtain the desired signal. For the filter to work well, the adaptive algorithm has to adjust the filter coefficients such that output of the filter is a good estimate of the noise present in the primary signal. To determine the amount by which noise in the primary signal is reduced, the mean squared error technique is used. The Minimum Mean Squared Error (MMSE) is defined as [42]: min E[d (n) − XW T ] 2 = min E[(d (n) − y (n)) 2 ] (3.1) where d is the desired signal, X and W are the vectors of the input reference signal and the filter coefficients respectively. This represents the measure of how well the newly constructed filter (given as a convolution product y(n) = XW) estimates the noise present in the primary signal. The goal is to reduce this error to a minimum. Therefore, the algorithms that perform adaptive noise cancellation are constantly searching for a coefficient vector W, which produces the minimum mean squared error. Minimizing the mean squared of the error signal minimizes the noise portion of the primary signal but not the desired portion. To understand this principle, recall that the primary signal is made of the desired portion and the noise portion. The filtered reference signal y(n) is a reference of the noise portion of the primary signal and therefore is correlated with it. However, the reference signal is not correlated with the desired portion of the primary signal. Therefore, minimizing the mean squared of the error signal minimizes only the noise in the primary signal. This principle can be mathematically described as follows: If we denote the desired portion of primary signal with s(n), and the noise portion of desired signal as x1(n), it follows that d(n) = s(n) + x1(n). As shown in Fig.3.3, the output of the system can be written as [43]: e(n) = d (n) − y (n) (3.2) e ( n ) = s ( n ) + x1 ( n ) − y ( n ) e(n) 2 = s (n) 2 + (( x1 (n) − y (n)) 2 + 2 s (n)(( x1 (n) − y (n)) E[e(n) 2 ] = E[ s (n) 2 ] + (( x1 (n) − y (n)) 2 + 2 s (n)(( x1 (n) − y (n)) 18
- 32. E[e(n) 2 ] = E[ s (n) 2 ] + E[(( x1 (n) − y (n)) 2 ] + 2 E[ s (n)(( x1 (n) − y (n))] (3.3) Due to the fact that the s(n) is un-correlated to both x1(n) and y(n), as noted earlier, the last term is equal to zero, so we have E[e(n) 2 ] = E[ s (n) 2 ] + E[(( x1 (n) − y (n)) 2 ] min E[e(n) 2 ] = min E[ s(n) 2 ] + min E[(( x1 (n) − y (n))2 ] (3.4) and since s(n) is independent of W, we have min E[e(n) 2 ] = E[ s (n) 2 ] + min E[(( x1 (n) − y (n)) 2 ] (3.5) Therefore, minimizing the error signal, minimizes the mean squared of the difference between the noise portion of the primary signal x1(n), and the filter output y(n) . 3.2 Approaches to Adaptive Filtering Algorithms Basically two approaches can be defined for deriving the recursive formula for the operation of Adaptive Filters. They are as follows: (i) Stochastic Gradient Approach: In this approach to develop a recursive algorithm for updating the tap weights of the adaptive transversal filter, the process is carried out in two stages. First we use an iterative procedure to find the optimum Wiener solution [43]. The iterative procedure is based on the method of steepest descent. This method requires the use of a gradient vector, the value of which depends on two parameters: the correlation matrix of the tap inputs in the transversal filter and the cross-correlation vector between the desired response and the same tap inputs. Secondly, instantaneous values for these correlations are used to derive an estimate for the gradient vector. Least Mean Squared (LMS) and Normalized Least Mean Squared (NLMS) algorithms lie under this approach and are discussed in subsequent sections. (ii) Least Square Estimation: This approach is based on the method of least squares. According to this method, a cost function is minimized that is defined as the sum of weighted error squares, where the error is the difference between some desired response and actual filter output. This method is formulated with block estimation in mind. In block estimation, the input data stream is arranged in the form of blocks of equal length (duration) and the filtering of input data proceeds on a block by block basis, which requires a large memory for computation. The Recursive Least Square (RLS) algorithm 19
- 33. falls under this approach and is discussed in subsequent section. 3.2.1 Least Mean Square (LMS) Algorithm The Least Mean Square (LMS) algorithm [1] was first developed by Widrow and Hoff in 1959 through their studies of pattern recognition [42]. Thereon it has become one of the most widely used algorithm in adaptive filtering. The LMS algorithm is a type of adaptive filter known as stochastic gradient-based algorithm as it utilizes the gradient vector of the filter tap weights to converge on the optimal wiener solution. It is well known and widely used due to its computational simplicity. With each iteration of the LMS algorithm, the filter tap weights of the adaptive filter are updated according to the following formula: w( n + 1) = w( n) + 2 μe( n ) x ( n) (3.6) where x(n) is the input vector of time delayed input values, and is given by x(n) = [ x(n) x(n − 1) x(n − 2)....x(n − N + 1)]T (3.7) w( n) = [ w0 ( n) w1 ( n) w2 ( n)....w N −1 (n)]T represents the coefficients of the adaptive FIR filter tap weight vector at time n and μ is known as the step size parameter and is a small positive constant. The step size parameter controls the influence of the updating factor. Selection of a suitable value for μ is imperative to the performance of the LMS algorithm. If the value of μ is too small, the time an adaptive filter takes to converge on the optimal solution will be too long; if the value of μ is too large the adaptive filter becomes unstable and its output diverges [14], [15], [22]. 3.2.1.1 Derivation of the LMS Algorithm The derivation of the LMS algorithm builds upon the theory of the wiener solution for the optimal filter tap weights, w0, as outlined above. It also depends on the steepest descent algorithm that gives a formula which updates the filter coefficients using the current tap weight vector and the current gradient of the cost function with respect to the filter tap weight coefficient vector, ξ(n). w(n + 1) = w(n) − μ∇ξ ( n) (3.8) 20
- 34. where ξ (n) = E[e 2 (n)] (3.9) As the negative gradient vector points in the direction of steepest descent for the N dimensional quadratic cost function each recursion shifts the value of the filter coefficients closer towards their optimum value which corresponds to the minimum achievable value of the cost function, ξ(n). The LMS algorithm is a random process implementation of the steepest descent algorithm, from Eq. (3.9). Here the expectation for the error signal is not known so the instantaneous value is used as an estimate. The gradient of the cost function, ξ(n) can alternatively be expressed in the following form: ∇ξ (n) = ∇(e 2 (n)) = ∂e 2 (n) / ∂w = 2e(n)∂e(n) / ∂w = 2e( n)∂[d ( n) − y ( n)] / ∂w = −2e(n)∂ewT (n).x(n)] / ∂w = −2 e ( n ) x ( n ) (3.10) Substituting this into the steepest descent algorithm of Eq. (3.9), we arrive at the recursion for the LMS adaptive algorithm. w( n + 1) = w( n) + 2 μe( n) x ( n) (3.11) 3.2.1.2 Implementation of the LMS Algorithm For the Implementation of each iteration of the LMS algorithm requires three distinct steps in the following order: 1. The output of the FIR filter, y(n) is calculated using Eq. (3.12). N −1 y (n) = ∑ w( n)x(n − i ) = wT (n) x(n) (3.12) i =0 2. The value of the error estimation is calculated using Eq. (3.13). 21
- 35. e( n ) = d ( n ) − y ( n ) (3.13) 3. The tap weights of the FIR vector are updated in preparation for the next iteration, by Eq. (3.14). w( n + 1) = w( n) + 2 μe( n) x ( n) (3.14) The main reason for the popularity of LMS algorithms in adaptive filtering is its computational simplicity that makes its implementation easier than all other commonly used adaptive algorithms. For each iteration, the LMS algorithm requires 2N additions and 2N+1 multiplications (N for calculating the output, y(n), one for 2μe(n) and an additional N for the scalar by vector multiplication) . 3.2.2 Normalized Least Mean Square (NLMS) Algorithm In the standard LMS algorithm when the convergence factor μ is large, the algorithm experiences a gradient noise amplification problem. In order to solve this difficulty we can use the NLMS algorithm [14]-[17]. The correction applied to the weight vector w(n) at iteration n+1 is “normalized” with respect to the squared Euclidian norm of the input vector x(n) at iteration n. We may view the NLMS algorithm as a time-varying step-size algorithm, calculating the convergence factor μ as in Eq. (3.15)[10]. μ ( n) = α c + x ( n) (3.15) 2 where α is the NLMS adaption constant, which optimize the convergence rate of the algorithm and should satisfy the condition 0<α<2, and c is the constant term for normalization and is always less than 1. The Filter weights are updated by the Eq. (3.16). w(n + 1) = w(n) + α c + x ( n) 2 e( n ) x ( n ) (3.16) It is important to note that given an input data (at time n) represented by the input vector x(n) and desired response d(n), the NLMS algorithm updates the weight vector in such a way that the value w(n+1) computed at time n+1 exhibits the minimum change with respect 22
- 36. to the known value w(n) at time n. Hence, the NLMS is a manifestation of the principle of minimum disturbance [3]. 3.2.2.1 Derivation of the NLMS Algorithm This derivation of the normalized least mean square algorithm is based on FarhangBoroujeny and Diniz [43]. To derive the NLMS algorithm we consider the standard LMS recursion in which we select a variable step size parameter, μ(n). This parameter is selected so that the error value, e+(n), will be minimized using the updated filter tap weights, w(n+1), and the current input vector, x(n). w(n + 1) = w(n) + 2 μ (n)e(n) x(n) e + (n) = d (n) − wT (n + 1) x(n) = (1 − 2 μ (n) xT (n) x(n))e(n) (3.17) Next we minimize (e+(n))2, with respect to μ(n). Using this we can then find a value for µ(n) which forces e+(n) to zero. μ ( n) = 1 2 x ( n ) x ( n) (3.18) T This μ(n) is then substituted into the standard LMS recursion replacing μ, resulting in the following. w(n + 1) = w(n) + 2 μ (n)e(n) x(n) 1 w(n + 1) = w(n) + T e( n) x ( n) x ( n) x ( n) w(n + 1) = w(n ) + μ (n) x(n ) (3.19) , where μ (n) = α x x+c T (3.20) Often the NLMS algorithm as expressed in Eq. (3.20 is a slight modification of the standard NLMS algorithm detailed above. Here the value of c is a small positive constant in order to avoid division by zero when the values of the input vector are zero. This was not implemented in the real time as in practice the input signal is never allowed to reach zero due to noise from the microphone and from the ADC on the Texas Instruments DSK. The parameter α is a constant step size value used to alter the convergence rate of the NLMS algorithm, it is within the range of 0<α<2, usually being equal to 1. 23
- 37. 3.2.2.2 Implementation of the NLMS Algorithm The NLMS algorithm is implemented in MATLAB as outlined later in Chapter 6. It is essentially an improvement over LMS algorithm with the added calculation of step size parameter for each iteration. 1. The output of the adaptive filter is calculated as: N −1 y (n) = ∑ w( n)x(n − i ) = wT (n) x(n) (3.21) i =0 2. The error signal is calculated as the difference between the desired output and the filter output given by: e( n) = d ( n ) − y ( n) (3.22) 3. The step size and filter tap weight vectors are updated using the following equations in preparation for the next iteration: For i=0,1,2,…….N-1 μ i ( n) = α c + xi ( n ) (3.23) 2 w(n + 1) = w(n) + μ i (n)e(n) xi (n) (3.24) where α is the NLMS adaption constant and c is the constant term for normalization. With α =0.02 and c=0.001, each iteration of the NLMS algorithm requires 3N+1 multiplication operations. 3.2.3 Recursive Least Square (RLS) Algorithm The other class of adaptive filtering technique studied in this thesis is known as Recursive Least Squares (RLS) algorithm [42]-[44]. This algorithm attempts to minimize the cost function in Eq. (3.25) where k=1 is the time at which the RLS algorithm commences and λ is a small positive constant very close to, but smaller than 1. With values of λ<1, more importance is given to the most recent error estimates and thus the more recent input samples, that results in a scheme which emphasizes on recent samples of observed data and tends to forget the past values. 24
- 38. n 2 ξ ( n) = ∑ λ n − k e n ( k ) (3.25) k =1 Unlike the LMS algorithm and NLMS algorithm, the RLS algorithm directly considers the values of previous error estimations. RLS algorithm is known for excellent performance when working in time varying environments. These advantages come at the cost of an increased computational complexity and some stability problems. 3.2.3.1 Derivation of the RLS Algorithm The RLS cost function of Eq. (3.25) shows that at time n, all previous values of the estimation error since the commencement of the RLS algorithm are required. Clearly, as time progresses the amount of data required to process this algorithm increases. Limited memory and computation capabilities make the RLS algorithm a practical impossibility in its purest form. However, the derivation still assumes that all data values are processed. In practice only a finite number of previous values are considered, this number corresponds to the order of the RLS FIR filter, N. First we define yn(k) as the output of the FIR filter, at n, using the current tap weight vector and the input vector of a previous time k. The estimation error value en(k) is the difference between the desired output value at time k and the corresponding value of yn(k). These and other appropriate definitions are expressed below, for k=1,2, 3,., n. yn (k ) = wT (n) x(k ) en (k ) = d (k ) − yn (k ) d (n) = [d (1), d (2).....d (n)]T y (n) = [ yn (1), yn (2)..... yn (n)]T e(n) = [en (1), en (2).....en (n)]T e( n ) = d ( n ) − y ( n ) (3.26) If we define X(n) as the matrix consisting of the n previous input column vector up to the present time then y(n) can also be expressed as Eq. (3.27). X (n) = [ x(1), x(2),....... x( n)] y (n) = X T (n) w(n) (3.27) 25
- 39. The cost function can be expressed in matrix vector form using a diagonal matrix, Λ(n) consisting of the weighting factors. n 2 ξ ( n) = ∑ λ n − k e n ( k ) k =1 ~ = eT (n)Λ (n)e(n) ⎡ λn −1 ⎢ ⎢ 0 ~ where Λ (n) = ⎢ 0 ⎢ ⎢ ... ⎢ 0 ⎣ 0 λ n−2 0 0 λn −3 0 ... 0 ... 0 0 0 0 ... 0 0 0 0 ... 1 ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ (3.28) Substituting values from Eq. (3.26) and (3.27), the cost function can be expanded and then reduced as in Eq. (3.29). (Temporarily dropping (n) notation for clarity). ~ ξ ( n ) = eT ( n ) Λ ( n ) e ( n ) ~ ~ ~ ~ = d T Λd − d T Λy − y T Λd + yT Λy ~ ~ ~ ~ = d T Λd − d T Λ ( X T w) − ( X T w)T Λd + ( X T w)T Λ ( X T w) ~ ~ ~ = d T Λd − 2θ w + wTψ w λ λ (3.29) where ~ ~ ψ λ = X ( n) Λ ( n) X T ( n) ~ ~ θ λ = X ( n) Λ ( n) d ( n) We derive the gradient of the above expression for the cost function with respect to the filter tap weights. By forcing this to zero we find the coefficients for the filter w(n), which minimizes the cost function. ~ ~ ψ λ (n) w(n) = θ λ (n) ~ −1 ~ w(n) = ψ λ (n)θ λ (n) (3.30) The matrix Ψ(n) in the above equation can be expanded and rearranged in recursive form. We can use the special form of the matrix inversion lemma to find an inverse for this matrix which is required to calculate the tap weight vector update. The vector k(n) is known as the gain vector and is included in order to simplify the calculation. 26
- 40. ~− ~− ψ λ 1 (n) = λψ λ 1 (n − 1) + x(n) xT (n) ~− = λ−1ψ λ 1 (n − 1) − ~− ~− λ− 2ψ λ 1 (n − 1) x(n) xT (n)ψ λ 1 (n − 1) ~− 1 + λ−1 xT (n)ψ λ 1 (n − 1) x(n) ~− ~− = λ−1 (ψ λ 1 (n − 1) − k (n) xT (n)ψ λ 1 (n − 1)) where ~− λ−1ψ λ 1 (n − 1) x(n) ~− 1 + λ−1 xT (n)ψ λ 1 (n − 1) x(n) k ( n) = ~− = ψ λ 1 ( n) x ( n) (3.31) The vector θλ(n) of Eq. (3.29) can also be expressed in a recursive form. Using this and substituting Ψ-1(n) from equation (3.31) into Eq. (3.30) we can finally arrive at the filter weight update vector for the RLS algorithm, as in Eq. (3.32). ~ ~ θ λ (n) = λθ λ (n − 1) + x(n)d (n) ~ −1 ~ w (n) = ψ (n)θ (n) λ ~ =ψ λ λ −1 ~ ~ ~ −1 (n − 1)θ λ (n − 1) − k (n) xTψ λ (n − 1)θ λ (n − 1) + k (n)d (n) = w (n − 1) − k (n) xT (n) w (n − 1) + k (n)d (n) = w (n − 1) + k (n)(d (n) − w T (n − 1) x(n)) w (n) = w (n − 1) + k (n)en −1 (n) (3.32) where en −1 (n) = d (n) − w T (n − 1) x(n) 3.2.3.2 Implementation of the RLS Algorithm: As stated previously, the memory of the RLS algorithm is confined to a finite number of values corresponding to the order of the filter tap weight vector. Two factors of the RLS implementation must be noted: first, although matrix inversion is essential for derivation of the RLS algorithm, no matrix inversion calculations are required for the implementation; thus greatly reducing the amount of computational complexity of the algorithm. Secondly, unlike the LMS based algorithms, current variables are updated within the iteration they are to be used using values from the previous iteration. To implement the RLS algorithm, the following steps are executed in the following order: 1. The filter output is calculated using the filter tap weights from the previous iteration and the current input vector. yn −1 (n) = w T (n − 1) x(n) (3.33) 27
- 41. 2. The intermediate gain vector is calculated using Eq. (3.34). −1 u (n) = wλ (n − 1) x(n) k (n) = u (n) /(λ + x T (n)u (n)) (3.34) 3. The estimation error value is calculated using Eq. (3.35). en −1 (n) = d (n) − yn −1 (n) (3.35) 4. The filter tap weight vector is updated using Eq. (3.36) and the gain vector calculated in Eq. (3.34). w(n) = w T (n − 1) + k (n)en −1 (n) (3.36) 5. The inverse matrix is calculated using Eq. (3.37). ψ λ −1 ( n) = λ −1 (ψ λ −1 ( n − 1) − k ( n)[ x T ( n)ψ λ −1 ( n − 1)] (3.37) When we calculate for each iteration of the RLS algorithm, it requires 4N2 multiplication and 3N2 addition operations. 3.3 Adaptive Filtering using MATLAB MATLAB is the acronym of Matrix Laboratory was originally designed to serve as the interactive link to the numerical computation libraries LINPACK and EISPACK that were used by engineers and scientists when they were dealing with sets of equations. The MATLAB software was originally developed at the University of New Mexico and Stanford University in the late 1970s. By 1984, a company was established named as Matwork by Jack Little and Cleve Moler with the clear objective of commercializing MATLAB. Over a million engineers and scientists use MATLAB today in well over 3000 universities worldwide and it is considered a standard tool in education, business, and industry. The basic element in MATLAB is the matrix and unlike other computer languages it does not have to be dimensioned or declared. MATLAB’s main objective was to solve mathematical problems in linear algebra, numerical analysis, and optimization but it quickly evolved as the preferred tool for data analysis, statistics, signal processing, control systems, economics, weather forecast, and many other applications. Over the years, MATLAB has evolved creating an extended library of specialized built-in functions that are used to generate among other things two-dimensional (2-D) and 3-D graphics and animation and offers 28
- 42. numerous supplemental packages called toolboxes that provide additional software power in special areas of interest such as• Curve fitting • Optimization • Signal processing • Image processing • Filter design • Neural network design • Control systems MATLAB Stand alone Application Simulink Application Development Stateflow Toolboxes Blocksets Data Sources Data Access Tools Student Products Code Generation Tools Mathworks Partner Products C Code Fig.3.4. MATLAB versatility diagram The MATLAB is an intuitive language and offers a technical computing environment. It provides core mathematics and advance graphical tools for data analysis visualization and algorithm and application development. The MATLAB is becoming a standard in industry, education, and business because the MATLAB environment is user-friendly and the objective of the software is to spend time in learning the physical and mathematical principles of a problem and not about the software. The term friendly is used in the following sense: the MATLAB software executes one instruction at a time. By analyzing the partial results and based on these results, new instructions can be executed that interact with the existing information already stored in the computer memory without the formal compiling required by other competing high-level computer languages. 29
- 43. Major Software Characteristics: i. Matrix based numeric computation. ii. High level programming language. iii. Toolboxes provide application-specific functionality. iv. Multiple Platform Support. v. Open and Extensible System Architecture. vi. Interfaces to other language (C, FORTRAN etc). For the simulation of the algorithms discussed in sec.3.2 MATLAB Version 7.4.0.287(R2007a) software is used. In the experimental setup, first of all high level MATLAB programs [5],[20] are written for LMS , NLMS and RLS algorithms as per the implementation steps described in sec.3.2.1.2, sec.3.2.2.2 and sec. 3.2.3.2 respectively [44] . Then the simulation of above algorithms is done with a noisy tone signal generated through MATLAB commands (refer sec. 6.1). The inputs to the programs are; the tone signal as primary input s(n), random noise signal as reference input x(n), order of filter (N), step size value (µ) ,number of iterations (refer Fig. 6.1) whereas the outputs are: the filtered output and MSE which can be seen in the graphical results obtained after simulation gets over( refer Fig.6.2). The output results for the MATLAB simulation of LMS, NLMS and RLS algorithm are presented and discussed later in the chapter-6. 30
- 44. Chapter-4 SIMULINK MODEL DESIGN FOR HARDWARE IMPLEMENTATION 4.1 Introduction to Simulink Simulink is a software package for modeling, simulating and analyzing dynamic systems [46]. It supports linear and nonlinear systems modeled in continuous time, sampled time, or a hybrid of the two. Systems can also be multi rate, i.e. have different parts that are sampled or updated at different rates. For modeling, simulink provides a graphical user interface (GUI) for building models as block diagrams, using click-and-drag mouse operations. With this interface, we can draw the models just as we would with pencil and paper (or as most textbooks depict them). Simulink includes a comprehensive block library of sinks, sources, linear and nonlinear components, and connectors. We can also customize and create our own blocks. Models are hierarchical, so we can build models using both top-down and bottom-up approaches. We can view the system at a high level and then double-click blocks to go down through the levels and thus visualize the model details. This approach provides insight into how a model is organized and how its parts interact. After we define a model, we can simulate it using a choice of integration methods either from the simulink menu or by entering commands in the MATLAB command window. In simulink, the menu is particularly convenient for interactive work. The command line approach is very useful for running a batch of simulations (for example, if we want to sweep a parameter across a range of values). Using scopes and other display blocks, we can see the simulation results while the simulation is running. In addition, we can change many parameters and see what happens. The simulation results can be put in the MATLAB workspace for post processing and visualization. The simulink model can be applied for modeling various time-varying systems that includes control systems, signal processing systems, video processing systems, image processing systems, communication and satellite systems, ship systems, automotive systems, monetary systems, aircraft & spacecraft dynamics systems, and biological systems as illustrated in Fig.4.1. 31
- 45. Fig.4.1. Simulink Applications 4.2 Model Design In the experimental setup for noise cancellation, simulink tool box has been used which provides the capability to model a system and to analyze its behavior. Its library is enriched with various functions which mimics the real system. The designed model for Adaptive Noise Cancellation (ANC) using simulink toolbox is shown in Fig.4.2. 4.2.1 Common Blocks used in Building Model 4.2.1.1 C6713 DSK ADC Block This block is used to capture and digitize analog signals from external sources such as signal generators, frequency generators or audio devices. Dragging and dropping C6713 DSK ADC block in simulink block diagram allows audio coder-decoder module (codec) on the C6713 DSK to convert an analog input signal to a digital signal for the digital signal processing. Most of the configuration options in the block affect the codec. However, the output data type, samples per frame and scaling options are related to the model that we are using in simulink. 32
- 46. Fig.4.2. Adaptive Noise Cancellation Simulink model 4.2.1.2 C6713 DSK DAC Block Simulink model provides the means to generate output of an analog signal through the analog output jack on the C6713 DSK. When C6713 DSK DAC block is added to the model, the digital signal received by the codec is converted to an analog signal. Codec sends signal to the output jack after converting the digital signal to analog form using digital-to-analog conversion (D/A). 4.2.1.3 C6713 DSK Target Preferences Block This block provides access to the processor hardware settings that need to be configured for generating the code from Real-Time Workshop (RTW) to run on the target. It is mandatory to add this block to the simulink model for the embedded target C6713. This block is located in the Target Preferences in Embedded Target for TI C6000 DSP for TI DSP library. 4.2.1.4 C6713 DSK Reset Block This block is used to reset the C6713 DSK to initial conditions from the simulink model. Double-clicking this block in a simulink model window resets the C6713 DSK that is running the executable code built from the model. When we double-click the Reset block, the 33
- 47. block runs the software reset function provided by CCS that resets the processor on C6713 DSK. Applications running on the board stop and the signal processor returns to the initial conditions that we defined. 4.2.1.5 NLMS Filter Block This block adapts the filter weights based on the NLMS algorithm for filtering the input signal. We select the adapt port check box to create an adapt port on the block. When the input to this port is nonzero, the block continuously updates the filter weights. When the input to this port is zero, the filter weights remain constant. If the reset port is enabled and a reset event occurs, the block resets the filter weights to their initial values. 4.2.1.6 C6713 DSK LED Block This block triggers the entire three user LEDs located on the C6711 DSK. When we add this block to a model and send a real scalar to the block input, the block sets the LED state based on the input value it receives: When the block receives an input value equal to 0, the LEDs are turned OFF. When the block receives a nonzero input value, the LEDs are turned ON. 4.2.1.7 C6713 DSK DIP Switch Block Outputs state of user switches located on C6713 DSK board. In boolean mode, output is a vector of 4 Boolean values, with the least-significant bit (LSB) first. In Integer mode, output is an integer from 0 to 15. For simulation, checkboxes in the block dialog are used in place of the physical switches. 4.2.2 Building the Model To create the model, first type simulink in the MATLAB command window or directly click on the shortcut icon . On Microsoft Windows, the simulink library browser appears as shown in Fig. 4.3. 34
- 48. Fig.4.3. Simulink library browser To create a new model, select Model from the New submenu of the simulink library window's File menu. To create a new model on Windows, select the New Model button on the Library Browser's toolbar. Simulink opens a new model window like Fig. 4.4. 35
- 49. Fig.4.4. Blank new model window To create Adaptive Noise Cancellation (ANC) model, we will need to copy blocks into the model from the following simulink block libraries: • Target for TI C6700 library (ADC, DAC, DIP, and LED blocks) • Signal processing library (NLMS filter block) • Commonly used blocks library (Constant block, Switch block and Relational block) • Discrete library (Delay block) To copy the ADC block from the Library Browser, first expand the Library Browser tree to display the blocks in the Target for TI C6700 library. Do this by clicking on the library node to display the library blocks. Then select the C6713 DSK board support sub library and finally, click on the respective block to select it. Now drag the ADC block from the browser and drop it in the model window. Simulink creates a copy of the blocks at the point where you dropped the node icon as illustrated in Fig.4.5. 36
- 50. Fig.4.5. Model window with ADC block Copy the rest of the blocks in a similar manner from their respective libraries into the model window. We can move a block from one place to another place by dragging the block in the model window. We can move a block a short distance by selecting the block and then pressing the arrow keys. With all the blocks copied into the model window, the model should look something like Fig.4.6. If we examine the block icons, we see an angle bracket on the right of the ADC block and two on the left of the NLMS filter block. The > symbol pointing out of a block is an output port; if the symbol points to a block, it is an input port. A signal travels out of an output port and into an input port of another block through a connecting line. When the blocks are connected, the port symbols disappear. Now it's time to connect the blocks. Position the pointer over the output port on the right side of the ADC block and connect it to the input port of delay, NLMS filter and switch block. Similarly make all connection as in Fig.4.2. 4.3 Model Reconfiguration Once the model is designed we have to reconfigure the model as per the requirement of the desired application. The simulink blocks parameters are adjusted as per the input output devices used. The input devices may be function generator or microphone and the output devices may be DSO or headphone respectively. This section explains and illustrates the reconfiguration setting of each simulink block like ADC, DAC, Adaptive filter, DIP, 37
- 51. LED, relational operator, switch block, and all that are used in the design of adaptive noise canceller. Fig.4.6. Model illustration before connections 4.3.1 The ADC Settings This block can be reconfigured to receive the input either from microphone or function generator. Input is applied through microphone when ADC source is kept at “Mic In” and through function generator when ADC source is kept at “Line In” as shown in Fig.4.7. The other settings are as follows: Double-click on the blue box to the left marked “DSK6713 ADC”. The screen as shown in Fig.4.7 will appear. Change the “ADC source” to “Line In” or “Mic In”. If we have a quiet microphone, select “+20dB Mic gain boost”. Set the “Sampling rate (Hz)” to “48 kHz”. Set the “Samples per frame” to 64. When done, click on “OK”. Important: Make sure the “Stereo” box is empty. 38
- 52. 4.3.2 The DAC Settings The DAC setting needs to be matched to those of the ADC. The major parameter is the sampling rate that is kept at the same rate of ADC i.e. 48 kHz as shown in Fig.4.8. Fig.4.7. Setting up the ADC for mono microphone input Fig.4.8. Setting the DAC parameters 39
- 53. 4.3.3 NLMS Filter Parameters Settings The most critical variable in an NLMS filter is the initial setup of “Step size (mu)”. If “mu” is too small, the filter has very fine resolution but reacts too slowly to the input signal. If “mu” is too large, the filter reacts very quickly but the error also remains large. The major parameters values that we have to change for the designed model are (shown in Fig.4.9): Step size (mu) = 0.001, Filter length =19 Select the Adapt port check box to create an Adapt port on the block. When the input to this port is nonzero, the block continuously updates the filter weights. When the input to this port is zero, the filter weights remain constant. Fig.4.9. Setting the NLMS filter parameters 40
- 54. 4.3.4 Delay Parameters Settings Delay parameter is required to delay the discrete-time input signal by a specified number of samples or frames. Because we are working with frames of 64 samples, it is convenient to configure the delay using frames. The steps for setting are described below and are illustrated in Fig. 4.10. Double-click on the “Delay” block. Change the “Delay units” to Frames. Set the “Delay (frames)” to 1. This makes the delay 64 samples. Fig.4.10. Setting the delay unit 4.3.5 DIP Switches Settings DIP switches are manual electric switches that are packaged in a group in a standard dual in-line package (DIP).These switches can work in two modes; Boolean mode, Integer mode. In Boolean mode, outputs are a vector of 4 boolean values with the least-significant bit (LSB) first. In Integer mode, outputs are an integer from 0 to 15. The DIP switches needs to be configured as shown in Fig. 4.11. 41
- 55. The “Sample time” should set to be “–1”. Fig.4.11. Setting up the DIP switch values 4.3.6 Constant Value Settings The switch values lie between 0 and 15. We will use switch values 0 and 1. For settings, Double-click on the “Constant” block. Set the “Constant value” to 1 and the “Sample time” to “inf” as shown in Fig.4.12. Fig.4.12. Setting the constant parameters 42
- 56. 4.3.7 Constant Data Type Settings The signal data type for the constant used in ANC model is set to “int16” as shown in Fig. 4.13. The setting of parameter can be done as follows: Click on the “Signal Data Types” tab. Set the “Output data type mode” to “int16”. This is compatible with the DAC on the DSK6713. Fig.4.13. Data type conversion to 16-bit integer 4.3.8 Relational Operator Type Settings Relational operator is used to check the given condition for the input signal. The relational operator setting for the designed model can be done as follows: Double click on the “Relational Operator” block. Change the “Relational operator” to “==”. Click on the “Signal Data Types” tab. 4.3.9 Relational Operator Data Type Settings Set the “Output data type mode” to “Boolean”. Click on “OK”. ( refer Fig.4.14) 43
- 57. Fig.4.14. Changing the output data type 4.3.10 Switch Settings The switch which is used in this model has three inputs viz. input 1, input 2 and input 3 numbered from top to bottom (refer Fig 4.2). The input 1 & input 3 are data inputs and input 2 is the control input. When input 2 satisfies the selection criteria, input 1 is passed to the output port otherwise input 3. The switch is configured as: Double click on the “switch” Set the criteria for passing first input to “u2>=Threshold” Click “ok” The simulink model for the hardware implementation of NLMS algorithm is designed successfully and the designed model is reconfigured to meet the requirement of TMS320C6713 DSP Processor environment. The reconfigured model shown in Fig.4.2 is ready to connect with Code Composer Studio [50] and DSP Processor with the help of RTDX link and Real-Time Workshop [47]. This is presented in chapter5. 44
- 58. Chapter-5 REAL-TIME IMPLEMENTATION ON DSP PROCESSOR Digital signal processors are fast special-purpose microprocessors with a specialized type of architecture and an instruction set appropriate for signal processing [45]. The architecture of the digital signal processor is very well suited for numerically intensive calculations. Digital signal processors are used for a wide range of applications which includes communication, control, speech processing, image processing etc. These processors have become the products of choice for a number of consumer applications, because they are very cost-effective and can be reprogrammed easily for different applications. DSP techniques have been very successful because of the development of low-cost software and hardware support [48]. DSP processors are concerned primarily with real-time signal processing. Real-time processing requires the processing to keep pace with some external event, whereas non-real-time processing has no such timing constraint. The external event is usually the analog input. Analog-based systems with discrete electronic components such as resistors can be more sensitive to temperature changes whereas DSP-based systems are less affected by environmental conditions. In this chapter we will learn how we can realize or implement an adaptive filter on hardware for real-time experiments. The model which was designed in previous chapter will be linked to the DSP processor with help of Real Time Data Exchange (RTDX) utility provided in simulink. 5.1 Introduction to Digital Signal Processor (TMS320C6713) The TMS320C6713 is a low cost board designed to allow the user to evaluate the capabilities of the C6713 DSP and develop C6713-based products [49]. It demonstrates how the DSP can be interfaced with various kinds of memories, peripherals, Joint Text Action Group (JTAG) and parallel peripheral interfaces. The board is approximately 5 inches wide and 8 inches long as shown in Fig.5.2 and is designed to sit on the desktop external to a host PC. It connects to the host PC through a USB port. The processor board includes a C6713 floating-point digital signal processor and a 45
- 59. 32-bit stereo codec TLV320AIC23 (AIC23) for input and output. The onboard codec AIC23 uses a sigma–delta technology that provides ADC and DAC. It connects to a 12-MHz system clock. Variable sampling rates from 8 to 96 kHz can be set readily [51]. A daughter card expansion is also provided on the DSK board. Two 80-pin connectors provide for external peripheral and external memory interfaces. The external memory interface (EMIF) performs the task of interfacing with the other memory subsystems. Lightemitting diodes (LEDs) and liquid-crystal displays (LCDs) are used for spectrum display. The DSK board includes 16MB (Megabytes) of synchronous dynamic random access memory (SDRAM) and 256kB (Kilobytes) of flash memory. Four connectors on the board provide inputs and outputs: MIC IN for microphone input, LINE IN for line input, LINE OUT for line output, and HEADPHONE for a headphone output (multiplexed with line output). The status of the four users DIP switches on the DSK board can be read from a program and provides the user with a feedback control interface (refer Fig.5.1 & Fig.5.2). The DSK operates at 225MHz.Also onboard are the voltage regulators that provide 1.26 V for the C6713 core and 3.3V for its memory and peripherals. The major DSK hardware features are: A C6713 DSP operating at 225 MHz. An AIC23 stereo codec with Line In, Line Out, MIC, and headphone stereo jacks. 16 Mbytes of synchronous DRAM (SDRAM). 512 Kbytes of non-volatile Flash memory (256 Kbytes usable in default configuration). Four user accessible LEDs and DIP switches. Software board configuration through registers implemented in complex logic device. Configurable boot options. Expansion connectors for daughter cards. JTAG emulation through onboard JTAG emulator with USB host interface or external Emulator. Single voltage power supply (+5V). 46
- 60. Fig.5.1. Block diagram of TMS320C6713 processor Fig.5.2. Physical overview of the TMS320C6713 processor 47
- 61. 5.1.1 Central Processing Unit Architecture The CPU has Very Large Instruction Word (VLIW) architecture [53]. The CPU always fetches eight 32-bit instructions at once and there is a 256-bit bus to the internal program memory. Each group of eight instructions is called a fetch packet. The CPU has eight functional units that can operate in parallel and are equally split into two halves, A and B. All eight units do not have to be given instruction words if they are not ready. Therefore, instructions are dispatched to the functional units as execution packets with a variable number of 32-bit instruction words. The functional block diagram of Texas Instrument (TI) processor architecture is shown below in Fig.5.3. 32 EMIF McASP1 McASP0 McBSP0 Pin Multiplexing I2C1 I2C0 Timer 1 Timer 0 Enhanced DMA Controller (16 Channel) McBSP1 L2 Cache Memory 4 Banks 64K Bytes Total (Up to 4‐ way) L2 Memory 192K Bytes C67x CPU Instruction Fetch Instruction Dispatch Instruction Decode Data Path A Data Path B A Register File B Register .L1 .S1 .M1 .D1 .D2 .M2 .S2 .L2 HPI Control Register Control Test In‐Circuit Emulation Interrupt Control L1D Cache 2‐Way Set Associative 4K Bytes Clock Generator Oscillator and PLL ×4 through ×25 Multiplier /1 through /32 Divider GPIO 16 LIP Cache Direct Mapped 4 Bytes Total Power – Down Logic Fig.5.3. Functional block diagram of TMS320C6713 CPU The eight functional units include: Four ALU that can perform fixed and floating-point operations (.L1, .L2, .S1, .S2). Two ALU’s that perform only fixed-point operations (.D1, .D2). 48
- 62. Two multipliers that can perform fixed or floating-point multiplications (.M1, .M2). 5.1.2 General Purpose Registers Overview The CPU has thirty two 32-bit general purpose registers split equally between the A and B sides. The CPU has a load/store architecture in which all instructions operate on registers. The data-addressing unit .D1 and .D2 are in charge of all data transfers between the register files and memory. The four functional units on a side freely share the 16 registers on that side. Each side has a single data bus connected to all the registers on the other side so that functional units on one side can access data in the registers on the other side. Access to a register on the same side uses one clock cycle while access to a register on the other side requires two clock cycles i.e. read and write cycle. 5.1.3 Interrupts The C6000 CPUs contain a vectored priority interrupt controller. The highest priority interrupt is RESET which is connected to the hardware reset pin and cannot be masked. The next priority interrupt is the NMI which is generally used to alert the CPU of a serious hardware problem like a power failure. Then, there are twelve lower priority maskable interrupts INT4–INT15 with INT4 having the highest and INT15 the lowest priority. Fig.5.4. Interrupt priority diagram 49
- 63. The following Fig. 5.5 depicts how the processor handles an interrupt when it arrives. Interrupt handling mechanism is a vital feature of microprocessor. Fig.5.5. Interrupt handling procedure These maskable interrupts can be selected from up to 32 sources (C6000 family). The sources vary between family members. For the C6713, they include external interrupt pins selected by the GPIO unit, and interrupts from internal peripherals such as timers, McBSP serial ports, McASP serial ports, EDMA channels, and the host port interface. The CPUs have a multiplexer called the interrupt selector that allows the user to select and connect interrupt sources to INT4 through INT15.As soon as the interrupt is serviced, processor resumes to the same operation which was under processing prior to interrupt request. 5.1.4 Audio Interface Codec The C6713 uses a Texas AIC23 codec. In the default configuration, the codec is connected to the two serial ports, McBSP0 and McBSP1. McBSP0 is used as a unidirectional channel to control the codec's internal configuration registers. It should be programmed to send a 16-bit control word to the AIC23 in SPI format. The top 7 bits of the control word specify the register to be modified and the lower 9 bits contain the register value. Once the 50
- 64. codec is configured, the control channel is normally idle while audio data is being transmitted. McBSP1 is used as the bi-directional data channel for ADC input and DAC output samples. The codec supports a variety of sample formats. For the experiments in this work, the codec should be configured to use 16-bit samples in two’s complement signed format. The codec should be set to operate in master mode so as to supply the frame synchronization and bit clocks at the correct sample rate to McBSP1. The preferred serial format is DSP mode which is designed specifically to operate with the McBSP ports on TI DSPs. The codec has a 12 MHz system clock which is same as the frequency used in many USB systems. The AIC23 can divide down the 12 MHz clock frequency to provide sampling rates of 8000 Hz, 16000 Hz, 24000 Hz, 32000 Hz, 44100 Hz, 48000 Hz, and 96000 Hz. DSK DSP CPU McBSP McBSP AIC23 Fig.5.6. Audio connection illustrating control and data signal The DSK uses two McBSPs to communicate with the AIC23 codec, one for control, another for data. The C6713 supplies a 12 MHz clock to the AIC23 codec which is divided down internally in the AIC23 to give the sampling rates. The codec can be set to these sampling rates by using the function DSK6713_AIC23_setFreq (handle,freq ID) from the BSL. This function puts the quantity “Value” into AIC23 control register 8. Some of the AIC23 analog interface properties are: The ADC for the line inputs has a full-scale range of 1.0 V RMS. 51
- 65. The microphone input is a high-impedance, low-capacitance input compatible with a wide range of microphones. The DAC for the line outputs has a full-scale output voltage range of 1.0 V RMS. The stereo headphone outputs are designed to drive 16 or 32-ohm headphones. The AIC23 has an analog bypass mode that directly connects the analog line inputs to the analog line outputs. The AIC23 has a side tone insertion mode where the microphone input is routed to the line and headphone outputs. AIC23 Codec FSX1 CLKX1 TX1 CONTROL SPI Format CS SCLK SD IN Digital Control Registers McBSP0 0 1 2 3 4 5 6 7 8 9 15 LEFT IN VOL RIGHT IN VOL LEFT HP VOL RIGHT HP VOL ANAPATH DIGPATH POWER DOWN DIGIF SAMPLE RATE DIGACT RESET DATA McBSP1 DR2 FX2 CLKR CLKX FSR2 DX2 D OUT LRC OUT B CLK LRC IN D IN MIC IN LINE IN Analog LINE OUT MIC IN ADC LINE IN DAC LINE OUT HP OUT HP OUT Fig.5.7. AIC23 codec interface 5.1.5 DSP/BIOS & RTDX The DSP/BIOS facilities utilize the Real-Time Data Exchange (RTDX) link to obtain and monitor target data in real-time [47]. I utilized the RTDX link to create my own customized interfaces to the DSP target by using the RTDX API Library. The RTDX transfers data between a host computer and target devices without interfering with the target application. This bi-directional communication path provides data collection by the host as well as host interaction while running target application. RTDX also enables host systems to provide data stimulation to the target application and algorithms. 52
- 66. Data transfer to the host occurs in real-time while the target application is running. On the host platform, an RTDX host library operates in conjunction with Code Composer Studio IDE. Data visualization and analysis tools communicate with RTDX through COM APIs to obtain the target data and/or to send data to the DSP application. The host library supports two modes of receiving data from a target application: continuous and non-continuous. Code Composer Studio CCS MATLAB Embedded Target for Texas Instruments DSP + Real Time Workshop Texas Instruments DSP Simulink Model Build and Download Application + DSP/BIOS Kernel RTDX DSP/BIOS Tools RTDX Fig.5.8. DSP BIOS and RTDX In continuous mode, the data is simply buffered by the RTDX Host Library and is not written to a log file. Continuous mode should be used when the developer wants to continuously obtain and display the data from a target application and does not need to store the data in a log file. The realization of an interface is possible thanks to the Real-Time Data Exchange (RTDX). RTDX allows transferring data between a host computer and target devices without interfering with the target application. The data can be analyzed and visualized on the host using the COM interface provided by RTDX. Clients such as Visual Basic, Visual C++, Excel, LabView, MATLAB, and others are readily capable of utilizing the COM interface. 53
- 67. 5.2 Code Composer Studio as Integrated Development Environment Code Composer Studio is the DSP industry's first fully integrated development environment (IDE) [50] with DSP-specific functionality. With a familiar environment like MS-based C++TM; Code Composer lets you edit, build, debug, profile and manage projects from a single unified environment. Other unique features include graphical signal analysis, injection/extraction of data signals via file I/O, multi-processor debugging, automated testing and customization via a C-interpretive scripting language and much more. Fig.5.9. Code compose studio platform Real-time analysis can be performed using real-time data exchange (RTDX). RTDX allows for data exchange between the host PC and the target DSK, as well as analysis in real time without stopping the target. Key statistics and performance can be monitored in real time. Through the joint team action group (JTAG), communication with on-chip emulation support occurs to control and monitor program execution. The C6713 DSK board includes a JTAG interface through the USB port. Fig.5.10. Embedded software development 54
- 68. Source Efficiency Effort Compiler Optimizer 80‐100% Low Linear ASM Assembly Optimizer 95‐100% Med ASM Hand Optimizer 100% High C C++ Fig.5.11. Typical 67xx efficiency vs. efforts level for different codes The Code composer studio supports three file formats (.c/c++, .sa, .asm) for writing codes. Fig.5.11 shows the efficiency vs. efforts level for three kinds of source codes. If we write the code in linear assembly then ASM optimizer is required to convert linear assembly file (.sa) to assembly file (.asm). Similarly if the code is written in C, the C compiler is required to produce an assembly source file with extension .asm. The assembler assembles .asm source file to produce a machine language object file with extension .obj. The linker combines object files and object libraries as input to produce an executable file with extension .out. This executable file represents a linked common object file format (COFF), popular in Unix-based systems and adopted by several digital signal processor developers [52]. This executable file can be loaded and run directly on the C6713 processor. Fig.5.12 and Fig.5.13 illustrate the process of target file generation. .sa ASM Optimizer Text Editor Link.cm Assembler .asm Linker .obj .c/.cpp .map Compiler Fig.5.12. Code generation 55 .out
- 69. C ASM File C Assembler Compiler Binary File Binary File Binary File Debugger Linker Profiler Library Exec. File Fig.5.13. Cross development environment To create an application project, one can “add” the appropriate files to the project. Compiler/linker options can readily be specified. A number of debugging features are available, including setting breakpoints and watching variables, viewing memory, registers, mixing C and assembly code, graphing results, and monitoring execution time. One can step through a program in different ways (step into, over, or out). Fig. 5.14 shows the signal flow during the processing. Fig.5.14. Signal flow during processing 56
- 70. Code composer features include: IDE with an editor, compiler, assembler, optimizer, debugger, etc. ‘C/C++’ compiler, assembly optimizes and linker. Simulator. Real-time operating system (DSP/BIOS™). Real-Time Data Exchange (RTDX™) between the host and target. Real-time analysis and data visualization. Advanced watch windows. Integrated editor. File I/O, Probe Points, and graphical algorithm scope probes. Advanced graphical signal analysis. Visual project management system. Multi-processor debugging. Fig.5.15. Real-time analysis and data visualization 57
- 71. 5.3 MATLAB interfacing with CCS and DSP Processor Fig.5.16. MATLAB interfacing with CCS and DSP processor Fig.5.16 depicts how the MATLAB is used as an interface for calling code composer studio (CCS) and then the program is loaded into the TI instrument target. First of all MATLAB code for the desired algorithm is written and then simulated for obtaining the results in MATLAB graph window. However if we want that the code written for MATLAB or the designed simulink model can be loaded in to the TI target then we can also perform some real time results depending upon the used algorithm. 5.4 Real-time Experimental Setup using DSP Processor The basic experimental setup for the hardware implementation of adaptive noise canceller is depicted in Fig.5.17 and the real image of setup is shown in Fig.5.18. The input signal can be provided to the DSP processor either through microphone or function generator on MIC IN or LINE IN port respectively. The development software, Code Composer Studio and simulation software MATLAB version 7.4 are installed on the PC and are used for coding the algorithm and linking the coded algorithm to the target processor. The input signal reaches to processor in digital form after the conversion by AIC23 onboard codec. The C code is generated using real-time workshop available in MATLAB & Simulink and loaded on the DSP processor. The input signal is processed according to code loaded into the processor memory. For interactive feedback 4 DIP switches can be used. When the signal processing is 58
- 72. completed the output can be taken at HP OUT or LINE OUT port with the help of headphone or CRO/DSO (refer Fig.5.17). Fig.5.17. Experimental setup using Texas Instrument processor Fig.5.18. Real-time experimental setup using DSP processor The real time implementation can be done in the following manner: First of all, the simulink model is developed (refer section 4.2) for NLMS algorithm and then connected to the CCS by RTDX link to create a project in the CCS as shown in Fig.5.19 [47]. 59
- 73. Fig.5.19. Model building using RTW When the link get establish the CCS opens, the project is created automatically and the process of code generation started as shown in Fig.5.20. Fig.5.20. Code generation using RTDX link 60
- 74. After code generation the code is compiled and during the compilation process compiler and debugger check the generated code for the errors. If there is any error code compile operation gets fail and gives the information about the error. Further these errors can be rectified and compilation process continues. When the compilation gets over the project is rebuild to generate .out executable file which is to be loaded on the target processor. Once the executable file is loaded in the processor memory, the processor is ready to use. Fig.5.21 shows the target processor in running position. Now the input can be applied to the processor through line-in port using a function generator and output can be taken from line-out port using DSO as shown in Fig.5.18. Fig.5.21. Target processor in running status If we investigate the simulink model (refer Fig.4.2), a DIP switch is used to control the flow of output signal and is configured as: When switch position is 0: The input of processor is directed toward output without filtering. The DIP switch at ‘Zero’ position is shown in Fig.5.22 (a).When Switch Position is 1: The NLMS filter start working and the output is the filtered version of input. The DIP switch at ‘one’ position is shown in Fig.5.22 (b). 61
- 75. Fig.5.22 (a) Switch at Position 0 Fig.5.22 (b) Switch at position 1 for NLMS noise reduction In this chapter an introduction of TMS320C6713 DSK hardware with features was presented. Then a brief introduction of the software environment CCStudio that used to build the project and create executable file for the DSP processor was also discussed. A model which was designed in previous chapter using simulink is connected to the DSP processor with the Real-Time Workshop (RTW) and the code is generated. The generated code is downloaded from host to target processor using RTDX link and run on processor. The output results are presented and discussed next in the chapter-6. 62
- 76. Chapter-6 RESULTS AND DISCUSSION In this chapter MATLAB simulation and real-time hardware implementation results for adaptive noise cancellation system are presented. The results are arranged in two sections; first section deals with the MATLAB simulation of LMS, NLMS and RLS adaptive filter algorithms when tone signal is applied as an input signal. A fair performance comparison of simulation results for all three algorithms is also presented in terms of mean squared error, computational complexity, percentage noise removal and stability. The next section shows the hardware implementation results for NLMS & LMS algorithms when implemented on TMS320C6713 DSP processor. Primarily the filtering is done for a tone signal. The effect of frequency and amplitude variation of a tone signal on the filter performance is also investigated. Further the filtering is done when an ECG signal is taken as an input to make the designed system more practical and implementable. Finally a SNR improvement comparison for NLMS and LMS algorithms is presented when ECG is taken as input signal and implemented on DSK hardware. 6.1 MATLAB Simulation Results for Adaptive Algorithms In the MATLAB simulation the reference input signal x(n) is a white Gaussian noise of power 2-dB generated using randn function, s(n) is a clean sinusoidal tone signal of amplitude 2V. The desired signal d(n) obtained by adding a delayed version of x(n) into clean signal s(n), d(n) = s(n) + x1(n) as shown in Fig.6.1. Fig.6.1. (a) Clean tone (sinusoid) signal s(n),(b)Noise signal x(n) 63
- 77. Fig.6.1. (c) Delayed noise signal x1(n), (d) desired signal d(n) 6.1.1 LMS Algorithm Simulation Results The simulation of the LMS algorithm is carried out with the following specifications: Filter order N=19, step size µ= 0.001, and iterations= 8000. Fig.6.2. MATLAB simulation for LMS algorithm; N=19, step size=0.001 The LMS algorithm is simple and easy to implement but the convergence speed is slow, it can be seen from the simulation results derived in Fig.6.2. The LMS based filter adopts the approximate correct output in 2800 samples as shown in Fig.6.2 (a), the corresponding mean squared error generated as per adaption of filter parameters is shown in Fig.6.2 (b). The average Mean Squared Error (MSE) achieved for LMS algorithm is 2.5×10-2. The value of MSE for LMS algorithm highly depends on the step size µ. This is illustrated in Fig 6.3, which is derived by the simulation of LMS algorithm at different values of step size, varied from 0.0001 to 0.01. The corresponding numeric data for the Fig.6.3 is presented in Table 6.1. 64
- 78. TABLE 6.1 MEAN SQUARED ERROR (MSE) VERSUS S TEP SIZE (µ) S.N. Step-size(µ) Mean Squared Error(MSE) 1. 0.0001 0.1281 2. 0.0002 0.0738 3. 0.0003 0.0516 4. 0.0004 0.0404 5. 0.0005 0.0340 6. 0.0006 0.0300 7. 0.0007 0.0275 8. 0.0008 0.0259 9. 0.0009 0.0249 10. 0.001 0.0244 11. 0.002 0.0308 12. 0.003 .0448 13. 0.004 0.0618 14. 0.005 0.0805 15. 0.006 0.1005 16. 0.007 0.1215 17. 0.008 0.1437 18. 0.009 0.1671 19. 0.01 0.1918 65
- 79. Fig.6.3. MSE versus step-size (µ) for LMS algorithm From Table 6.1 and Fig.6.3 it is clear that when the value of µ is too small (0.0001) the mean squared error is too large (0.1281). As we increase the step-size, the mean squared error gets reduced but after a limit (µ=0.001) the mean squared error starts increasing as we increase the step-size (µ>0.001). Hence the selection of the proper value of step-size for specific application is prominent in getting good results. 6.1.2 NLMS Algorithm Simulation Results The simulation of the NLMS algorithm is also carried out with the same parameters as for LMS algorithm: Filter order N=19, step size µ= 0.001 and iterations= 8000. In case of NLMS algorithm step size is not fixed, it varies at each iteration on the basis of the input signal energy. Therefore the filter performance improves and less time is required as compared to LMS algorithm to converge on the optimum solution. The NLMS based filter adopt the approximate correct output in 2300 samples as shown in Fig.6.4 (a), the corresponding mean squared error generated as per adaption of filter parameters is shown in Fig.6.4 (b). The average MSE achieved for NLMS algorithm is 2.1×10-2. 66
- 80. Fig.6.4. MATLAB simulation for NLMS algorithm; N=19, step size=0.001 6.1.3 RLS Algorithm Simulation Results The simulation of the RLS algorithm is carried out with the following specifications: Filter order N=19, iterations= 8000, and a positive constant λ=1. Fig.6.5. MATLAB simulation for RLS algorithm; N=19, λ=1 The RLS algorithm is much faster and produces a minimum mean squared error , it can be seen in Fig.6.5. The RLS based filter adopt the approximate correct output in 300 samples as shown in Fig.6.5 (a), the corresponding mean squared error generated as per adaption of filter parameters is shown in Fig.6.5 (b). The average MSE achieved for RLS algorithm is 1.7×10-2. 6.1.4 Performance Comparison of Adaptive Algorithms If we compare the filtered output and mean squared error of all algorithms(refer Fig.6.2,Fig.6.4, Fig.6.5), LMS adopt the approximate correct output in 2800 samples with an average MSE of 2.5×10-2, NLMS adopt in 2300 samples with an average MSE of 2.1×10-2 and RLS adopt in 300 samples with an average MSE of 1.7×10-2. This shows that RLS has 67
- 81. faster learning rate with least MSE. But in practical applications the implementation of RLS algorithm is limited due to the larger computational complexity and memory requirements. The filter order also affects the performance of a noise cancellation system. Fig.6.6 illustrates how the MSE changes as we change filter order. When filter order is less (<15), LMS has good MSE as compared to NLMS and RLS but as the filter order increases (>15) the performance of RLS becomes better and LMS has poor performance. It justifies the fact that the selection of right filter order is necessary to achieve the best performance. In this work the appropriate filter order is 19 therefore all simulations are carried out at N=19. Fig.6.6. MSE versus filter order (N) For proper filtering filter order should be higher but as we increase the filter order the convergence speed of the filter get slower, therefore a proper selection of filter order and suitable adaptive algorithm is imperative to the performance of the system. Table 6.2 illustrates the performance comparison of LMS, NLMS and RLS algorithms in terms of MSE when filter order is changed. 68
- 82. TABLE 6.2 MEAN SQUARED ERROR (MSE) VERSUS FILTER-ORDER (N) S.N 1. 2. 3. Filter-order(N) 1 2 3 MSE (LMS) 0.3044 0.3061 0.3075 MSE(NLMS) 0.6092 0.4261 0.3699 MSE(RLS) 0.3059 0.3123 0.3121 4. 5. 6. 7. 4 5 6 7 0.3088 0.3098 0.3104 0.3113 0.3487 0.3408 0.3380 0.3352 0.3082 0.3059 0.2977 0.3121 8. 9. 10. 11. 8 9 10 11 0.3127 0.3135 0.3143 0.3142 0.3330 0.3305 0.3280 0.3250 0.3103 0.3109 0.3139 0.3249 12. 13. 14. 15. 12 13 14 15 0.3146 0.3094 0.3105 0.2508 0.3227 0.3155 0.3146 0.2524 0.3032 0.3394 0.3207 0.2448 16. 17. 18. 19. 16 17 18 19 0.1001 0.0408 0.0421 0.0374 0.0995 0.0388 0.0394 0.0344 0.0914 0.0390 0.0254 0.0188 20. 21. 22. 23. 20 21 22 23 0.0384 0.0382 0.0394 0.0401 0.0349 0.0344 0.0355 0.0358 0.0214 0.0278 0.0312 0.0264 24. 25. 26. 27. 24 25 26 27 0.0411 0.0420 0.0430 0.0441 0.0363 0.0367 0.0373 0.0380 0.0232 0.0400 0.0440 0.0468 28. 29. 30. 31. 28 29 30 31 0.0452 0.0463 0.0473 0.0483 0.0388 0.0397 0.0405 0.0412 0.0407 0.0531 0.0342 0.0344 32. 33. 32 33 0.0492 0.0501 0.0418 0.0425 0.0469 0.0476 69
- 83. S.N 34. 35. 36. Filter-order(N) 34 35 36 MSE (LMS) 0.0509 0.0519 0.0529 MSE(NLMS) 0.0435 0.0446 0.0456 MSE(RLS) 0.0500 0.0542 0.0577 37. 38. 39. 40. 37 38 39 40 0.0539 0.0547 0.0555 0.0563 0.0464 0.0469 0.0476 0.0484 0.0594 0.0604 0.0663 0.0777 41. 42. 43. 44. 41 42 43 44 0.0571 0.0580 0.0589 0.0598 0.0493 0.0501 0.0510 0.0518 0.0953 0.1142 0.1185 0.1231 45. 45 0.0606 0.0525 0.1350 TABLE 6.3 PERFORMANCE COMPARISON OF VARIOUS ADAPTIVE ALGORITHMS S.N Algorithm MSE 1. LMS 2. 3. % Noise Reduction Complexity (No. of multiplications per Stability 2.5×10-2 91.62% 2N+1 Highly Stable -2 93.85% 3N+1 Stable 2.1×10 NLMS -2 1.7×10 RLS 98.78% 4N 2 less Stable TABLE 6.4 COMPARISON OF VARIOUS PARAMETERS FOR ADAPTIVE ALGORITHMS Algorithm LMS NLMS RLS Convergence Time Very slow Slow Fast Complexity Very Simple Simple High MIPS consumption Very Low Low High Implementation Very Simple Simple Complex Parameters 70
- 84. Table 6.3 and Table 6.4 represent the performance analysis of adaptive filter algorithms. In Table 6.3 performance analysis of all three algorithms is presented in term of MSE, percentage noise reduction, computational complexity and stability. It is clear from the Table 6.3 that computational complexity and stability problems increases in an algorithm as we try to reduce the mean squared error. The LMS algorithm has 2N+1 number of multiplications at each iteration with 91.62% noise reduction. The NLMS algorithm has 3N+1 number of multiplications at each iteration with 93.85% noise reduction. The RLS algorithm has 4N2 number of multiplications at each iteration with 98.78% noise reduction. These results shows that the noise reduction in RLS algorithm is highest but at the same time computational complexity is also higher and also encounters stability problems sometimes. NLMS algorithm has only N number of additional multiplications as compared to LMS algorithm for better filtering and is stable, less complex as compared to RLS algorithm. Therefore, NLMS is the favorable choice for most of the industries and practical applications. 6.2 Hardware Implementation Results using TMS320C6713 Processor The experimental setup for real-time noise cancellation is depicted in Chapter 5 (Fig.5.18). The model is created in simulink and is connected to the TMS320C6713 processor using real-time workshop (refer Fig.5.19). The model is tested with two types of signals viz. tone signal and ECG signal. The output results are measured with the help of DSO. 6.2.1 Tone Signal Analysis using NLMS Algorithm In this section real-time results of DSP Processor for a tone (sinusoidal) signal are presented. Initially a clean tone-signal of 2-dB power and 1 kHz frequency as shown in Fig.6.7 is generated using function generator and then random noise is added to it with the help of noise generator so the signal becomes a noisy signal as illustrated in Fig. 6.8.This noisy signal is applied at the “Line In” port of DSK, which is processed as per the program running on the DSK and the filtered output is taken from “Line Out” port of the processor kit. A MATLAB program is written to calculate the SNR of the noisy signal and filtered signal. The filtered output in Fig.6.9 shows a considerable improvement in the signal quality with an average SNR improvement of 11dB. 71
- 85. Fig.6.7. Clean tone signal of 1 kHz Fig.6.8. Noise corrupted tone signal Fig. 6.10 illustrates the time delay introduced by hardware components where the filtered output is delayed by a period of 0.4ms. The delay time between the desired signal and the filtered signal is very short which enables the noise-cancellation in real-time. Although the power of filtered signal is reduced but the accuracy in filtered signal is excellent. The reduced power of the filtered signal can be amplified by the amplifier as per the requirement of the application. 72
- 86. Fig.6.9. Filtered tone signal Fig.6.10. Time delay in filtered signal 6.2.1.1 Effect on Filter Performance at Various Frequencies Investigations are carried out for the tone signals at various frequencies. When we increase the signal frequency the voltage level gets reduced which has to be maintained at certain level. Here the voltage level is kept at 2V for the sake of experimentation and the frequencies are varied from 2 kHz to 5 kHz. The effect of frequency variations on the filter performance can be visualized in the Fig. 6.11. 73
- 87. Fig.6.11. (a) Filtered output signal at 2 kHz frequency Fig.6.11. (b) Filtered output signal at 3 kHz frequency Fig. 6.11 illustrates how the noisy signal and its filtering gets affected as we increase the frequency of the clean signal. When we increase the frequency, the noise component in desired signal gets increased or decreased as per the frequency correlation of noise and clean signal. When the noise lies in the same frequency band of clean signal, signal gets more noisy and results in poor filtering as shown in Fig.6.11 (d), When the frequency of noise and clean signal is not matched, the desired signal is less affected by the noise and results in fine filtering as illustrated in Fig. 6.11 (a), Fig.6.11 (b) & Fig. 6.11 (c). 74
- 88. Fig.6.11. (c) Filtered output signal at 4 kHz frequency Fig.6.11. (d) Filtered output signal at 5 kHz frequency 6.2.1.2 Effect on Filter Performance at Various Amplitudes Now some other kinds of measurements are taken to check effect of noise on the filtered signal when the amplitude of clean signal is varied. The tone signal frequency is fixed at 1 kHz and the amplitude of tone signal is varied from 3V to 5V. 75
- 89. Fig.6.12. (a) Filtered output signal at 3V Fig.6.12. (b) Filtered output signal at 4V When the amplitude of clean tone signal is increased the comparative amplitude of noise get reduced which marginally effects the clean signal and results in a higher degree of SNR improvement up to 13dB. Fig. 6.12 shows the corresponding waveforms. 76
- 90. Fig.6.12. (c) Filtered output signal at 5V Fig.6.13. Filtered signal at high noise The investigation so far carried out for tone signal was based on low or medium noise environments where the obtained result shows a reasonable level of SNR improvement. Fig.6.13 shows the system consistency in high level noise environment by making an average SNR improvement of 10dB for filtered signal. A tabular presentation of SNR improvement versus frequency & amplitude variations is presented in Table 6.5 and SNR Improvement versus Noise Level is presented in Table 6.6. 77
- 91. TABLE 6.5 SNR IMPROVEMENT VERSUS VOLTAGE AND FREQUENCY S.N. Amplitude (V) Frequency (kHz) SNR Improvement (dB) 1. 2 1 11.00 2. 3 1 11.52 3. 4 1 11.93 4. 5 1 12.80 5. 2 2 11.58 6. 2 3 11.93 7. 2 4 12.08 8. 2 5 11.66 TABLE 6.6 SNR IMPROVEMENT VERSUS NOISE LEVEL FOR A TONE SIGNAL S.N. Noise Level Noise Variance SNR Improvement (dB) 1. Low 0.02 13 2. Medium 0.05 12 3. High 0.15 10 6.2.2 ECG Signal Analysis using NLMS and LMS Algorithms and their Performance Comparison The ECG or the electrocardiogram is a biomedical signal. It is the electrical manifestation of the contractile activity of the heart. ECG is a quasi- periodical, rhythmically repeating signal, synchronized by the function of the heart which acts as the generator of bioelectrical events. A typical ECG cycle is defined by the various features (P, Q, R, S, and T) of the electrical wave. 78
- 92. Fig.6.14. ECG waveform The P wave marks the activation of the atria, which are the chambers of the heart that receive blood from the body. The activation of the left atrium which collects oxygen-rich blood from the lungs and the right atrium which gathers oxygen-deficient blood from the body takes about 90 msec. Next in the ECG cycle comes the QRS complex. The heart beat cycle is measured as the time between the second of the three parts of the QRS complex, the large R peak. The QRS complex represents the activation of the left ventricle which sends oxygen-rich blood to the body, and the right ventricle which sends oxygen-deficient blood to the lungs. During the QRS complex, which lasts about 80 msec, the atria prepare for the next beat, and the ventricles relax in the long T wave. These are the features of the ECG signal by which a cardiologist uses to analyze the health of the heart and note various disorders, such as atrial flutter, fibrillation, and bundle branch blocks. The ECG signal is a very weak time varying signal (about 0.5mV) and has a frequency between 0.5Hz to 100Hz. Therefore it is more prone to interference from the environmental noise. Thus the waveforms recorded have been standardized in terms of amplitude and phase relationships and any deviation from this would reflect the presence of an abnormality. Abnormal patterns of ECG may be due to undesirable artifacts, Normally ECG is contaminated by power-line interference of 50Hz. So it is desired to eliminate this noise and to find how best the signal can be improved. 79
- 93. In this section, an attempt is made to denoise an ECG signal with the help of Least Mean Square based adaptive filters implemented on TMS320C6713 DSP processor in realtime environment. Then a performance comparison of NLMS & LMS algorithms based on average SNR improvement is presented for a real-time biomedical signal. Fig.6.15 shows a clean (amplified) ECG signal with 1000 sample values of amplitude 260mV and frequency 35 Hz generated through twelve lead configurations, sampled at a frequency of 1.5 kHz. Fig.6.15. Clean ECG signal The NLMS & LMS based designed adaptive filter models are tested for three levels (low, medium and high) of noise corrupted ECG signals. The samples of noisy and filtered ECG signals are stored in a comma separated value (.csv) file with the help of DSO. This (.csv) file is used in a MATLAB program to calculate SNR before filtering and after filtering, which gives an estimate of an average SNR improvement in the filtered signal. If we analyse the filtered output of low noise ECG signal (Fig.6.16), we find that there is a high degree of filtering with an average SNR improvement of 9.89 dB for NLMS and 8.85 dB for LMS algorithms. This shows that the filtered signal is approximately equal to the clean signal. 80
- 94. Fig.6.16. (a) NLMS filtered output for low level noisy ECG signal Fig.6.16. (b) LMS filtered output for low level noisy ECG signal In the second case (refer Fig.6.17), when medium level of noise contaminates the signal, the average SNR improvements in filtered signals are 8.62 dB and 7.55 dB for NLMS & LMS algorithms respectively. The last case (refer Fig.6.18) deals with high level of noisy environment where due to noise, the peaks of R wave matches with the peaks of T wave which makes it difficult to measure the heart rate of a patient because heart rate is measured with help of peaks of QRS complex. 81
- 95. Fig.6.17. (a) NLMS filtered output for medium level noisy ECG signal Fig.6.17. (b) LMS filtered output for medium level noisy ECG signal The problem is solved in the filtered signal (Fig.6.18) which preserves the peaks of each QRS complex and cuts down the peak of noisy T waves with an average SNR improvement of 6.38 dB & 5.12 dB for NLMS & LMS algorithm respectively. 82
- 96. Fig.6.18. (a) NLMS filtered output for high level noisy ECG signal Fig.6.18. (b) LMS filtered output for high level noisy ECG signal In Table 6.7, an analysis of SNR Improvement is presented with respect to the noise variance for NLMS filtered and LMS filtered waves. It is clear from the Table 6.7, the performance of NLMS algorithm based filter is much better than LMS based filter with an average SNR difference upto 1.26 dB. 83
- 97. TABLE 6.7 SNR IMPROVEMENT VERSUS NOISE VARIANCE FOR AN ECG S IGNAL S.N. Noise Variance Sampling Rate (kHz) SNR Improvement NLMS (dB) SNR Improvement LMS (dB) 1. 0.02 1.5 9.89 8.85 2. 0.05 1.5 8.62 7.55 3. 0.1 1.5 6.38 5.12 The above results justify that the proposed real-time hardware implementation of NLMS algorithm shows a considerable improvement in the SNR of a noisy signal and the performance of the proposed system is better than the available LMS based systems. The hardware implementation of NLMS algorithm enables one to work with real-time biomedical and other kind of signals whereas simulation does not provide real-time working environment. The background noise for tone and ECG signals were eliminated adequately with reasonable rate for all the tested noises. When system is tested with tone signal in low and medium power noises, the system showed SNR improvement upto 13 dB and in high power noise environment SNR improvement is of 10 dB. When the measurements are carried out with a biomedical ECG signal, the SNR improvement is achieved upto 9.89 dB at low, 8.62 dB at medium noise and 6.38 dB for high noise environment. The filtered output preserves all the parameters of biomedical signal which are used for diagnosis purpose. Therefore based on these results, the designed system proves to be successful in the removal of noise form a desired signal such as ECG signal or any other type of biomedical diagnostic signal. 84
- 98. Chapter-7 CONCLUSIONS 7.1 Conclusion In the present work three adaptive filter algorithms; LMS, NLMS & RLS are implemented on MATLAB and the simulation results are analyzed for a tone signal. A fair performance comparison has been presented among the discussed algorithms based on the popular performance indices like Mean Squared Error (MSE), convergence speed, computational complexity etc. The simulation results show that the LMS algorithm has slow convergence, high MSE (2.5×10-2) but it is simple to implement and gives good results if step size is chosen correctly. The RLS algorithm has the highest convergence speed, less MSE (1.7×10-2) but at the cost of large computational complexity and memory requirement that makes it difficult to realize on the hardware. In case of NLMS algorithm, the MSE is 2.1×10-2, hence its performance lies between LMS and RLS algorithms. Therefore it provides a trade-off in convergence speed and computational complexity. The NLMS and LMS algorithms are then implemented on the TMS320C6713 processor for real-time noise cancellation. The filter performance is measured in terms of SNR improvement. The results were analyzed for two types of signals; tone signal and ECG signal with the help of DSO. The tone signal has been analyzed at various frequencies and voltage level to check the effect of noise on the filtering. We find that the effect of noise gets more prominent when the frequency of noise and clean signal is highly correlated or noise signal has higher amplitude. The designed system is further tested for three ECG signals of different noise level for NLMS algorithm and LMS algorithm. A fair amount of SNR improvement (upto 9.89 dB and 8.85 dB respectively) is achieved in both algorithms and the filtered ECG signal was found useful for medical diagnosis purposes. When the results of two algorithms were compared, it is found that the NLMS algorithm has shown better performance with the advancement of 1.26 dB in the average SNR improvement. 85
- 99. 7.2 Future Scope Considering the nature of the experiment, there are a number of viable directions for the extension of the research. An interesting extension would be implementing different kind of adaptive filter algorithms like Time Varying LMS (TVLMS), Variable Step Size NLMS (VSSNLMS), Fast Transversal RLS (FTRLS) etc. that may perform with faster convergence and better noise reduction. Another useful extension of this thesis would be in the use of larger number of filter coefficients. Depending on the application, many of the adaptive filters in practice use a large number of filter coefficients. This is necessary when the time delay spread of a system is large requiring long filters as in the case of noise cancellation. It is common to find the filters of order 2048 or larger. In such applications, the convergence speed is significantly slower than it is for the shorter filter lengths. Therefore, in those cases the convergence speed and the ways to improve performance becomes a critical factor. Performing this experiment, however, requires redesigning the current hardware platform enabling the use of more powerful processor that could handle the extended computational load. There are many other possibilities for further development in this discipline. Some of them are as follows: The noise cancellation system was implemented successfully using the TMS320C6713 DSK. However, the system was implemented using auto C code generation which takes more memory on the board which limits the hardware performance. Coding in assembler could allow for further optimization and an improvement in the systems performance. The implemented noise cancellation system is mainly analysed for tone signals and ECG signals. However someone can also analyse it for other kind of noise corrupted signals. The noise cancellation system was developed on the DSK board. This has certain parameters such as sampling rate that are unalterable by the developer. Another possible way to increase the performance of the noise cancellation system is to use the 86
- 100. C6713 digital signal processor in a custom made circuit which can properly utilize its full potential. This thesis deals with transversal FIR adaptive filters; this is only one of many methods of digital filtering. Other techniques such as infinite impulse response (IIR) or lattice filtering may prove to be more effective in an adaptive noise reduction application but ask for enough memory requirements. The algorithms studied in this thesis perform best under purely stationary signal conditions. Further work could be done in developing techniques specifically designed for non-stationary signals. For different applications, different characteristics and performance measures are important. Wavelet transforms can give advantages and disadvantages in different aspects of the application. Such an experiment could be done on the same or similar hardware as the one used in this experiment. I feel that the goals of this thesis have been accomplished. But, the field of digital signal processing and in particular adaptive filtering is vast and further research and development in this discipline can only lead to an improvement on the methods for Adaptive noise cancellation systems studied in this dissertation. 87
- 101. REFERENCES REFERENCE FROM PAPERS & JOURNALS: [1] Bernard Widrow, John R. Glover, John M. Mccool, John Kaunitz, Charles S. Williams, Robert H. Hean, James R. Zeidler, Eugene Dong, Jr. and Robert C. Goodlin, “Adaptive Noise Cancelling: Principles and Applications”, Proceedings of the IEEE, vol.-63 , no.-12 , pp. 1692-1716, December 1975. [2] Abutaleb, A.S, “An adaptive filter for noise cancelling”, IEEE Transactions on Circuits and Systems, vol.-35, no.-10, pp. 1201-1209, October 1988. [3] Abhishek Tandon, M. Omair Ahmad, “An efficient, low-complexity, Normalized LMS algorithm for echo cancellation” The 2nd Annual IEEE Northeast Workshop on Circuits and Systems, pp. 161-164, June 2004. [4] DONG Hang and SUN Hong, “Multirate Algorithm for Updating the Coefficients of Adaptive Filter”, First International Conference on Intelligent Networks and Intelligent Systems, pp. 581-584, November 2008. [5] Ying He, Hong He, Yi Wu and Hongyan Pan, “The Applications and Simulation of Adaptive Filter in Noise Canceling”, International Conference on Computer Science and Software Engineering, vol.-4, pp. 1-4, December 2008. [6] Edgar Andrei Vega Ochoa and Manuel Edgardo Guzman Renteria, “A real time acoustic echo canceller implemented on the Motorola DSP56307”, IEEE International Symposium on Industrial Electronics, vol.-2, pp. 625-630, December 2000. [7] Michail D. Galanis and Athanassios Papazacharias, “A DSP Course for Real-Time Systems Design and Implementation based on TMS320C6211 DSK”, 14th International Conference on Digital Signal Processing, vol.-2, pp. 853-856, December 2002. [8] Boo-Shik Ryu, Jae-Kyun Lee, Joonwan Kim, Chae-Wook Lee, “The Performance of an adaptive noise canceller with DSP processor”, 40th IEEE Southeastern Symposium on System Theory, pp. 42-45, March 2008. [9] Gerardo Avalos, Daniel Espinobarro, Jose Velazquez, Juan C. Sanchez, “Adaptive Noise Canceller using LMS algorithm with codified error in a DSP”, 52nd IEEE International Midwest Symposium on Circuits and Systems, pp. 657-662, August 2009. [10] J.C. Duran Villalobos, C.A., Tavares Reyes, J.A., Sanchez Garcia, “Implementation and Analysis of the NLMS Algorithm on TMS320C6713 DSP”, 52nd IEEE International Midwest Symposium on Circuits and Systems, pp. 1091-1096, August 2009. 88
- 102. [11] Gaurav Saxena, Subramaniam Ganesan, and Manohar Das, “Real time implementation of adaptive noise cancellation”, IEEE International conference on electro/information technology, pp. 431-436, May 2008. [12] Hasnain, S.K. Daruwalla, A.D. Saleem, “A unified approach in audio signal processing using the TMS320C6713 and simulink blocksets”, 2nd International Conference on Computer, Control and Communication, pp. 1-5, February 2009. [13] Yaghoub Mollaei, “Hardware Implementation of Adaptive filters”, Proceedings of IEEE Student Conference on Research and Development, UPM Serdang, Malaysia, pp. 45-48, November 2009. [14] Slock, D.T.M., “On the convergence behavior of the LMS and the normalized LMS algorithms”, IEEE Transactions on Signal Processing, vol.- 41, no.- 9, pp. 2811-2825, September 1993. [15] Sanaullah Khan, M.Arif and T.Majeed, “Comparison of LMS, RLS and Notch Based Adaptive Algorithms for Noise Cancellation of a typical Industrial Workroom”, 8th International Multi-topic Conference, pp. 169-173, December 2004. [16] Yuu-Seng Lau, Zahir M. Hussian and Richard Harris, “Performance of Adaptive Filtering Algorithms: A Comparative Study”, Australian Telecommunications, Networks and Applications Conference (ATNAC), Melbourne, 2003. [17] Thomas Schertler, “Selective Block Update of NLMS type Algorithms”, IEEE International Conference on Acoustics, Speech and Signal Processing, vol.-3, pp. 17171720, May1998. [18] Andy W. H. Khong, “Stereophonic Acoustic Echo Cancellation Employing SelectiveTap Adaptive Algorithms”, IEEE Transactions on Audio, Speech, and Language Processing, vol.- 14, no.- 3, pp. 785-796, May 2006. [19] Amit S. Chhetri, Jack W. Stokes, Dinei A. Florˆencio, “Acoustic Echo Cancelation for High Noise Environments”, IEEE International Conference on Multimedia and Expo, pp. 905-908, July 2006. [20] Amrita Rai and Amit Kumar Kohli, “Analysis and Simulation of Adaptive Filter with LMS Algorithm”, International Journal of Electronics Engineering, vol.-2, no.-1, pp. 121-123, January 2010. [21] J. Benesty , F. Amand , A. Gilloire and Y. Grenier , “Adaptive Filtering Algorithms for Stereophonic Acoustic Echo Cancellation”, International Conference on Acoustics, Speech, and Signal Processing, vol.-5, pp. 3099-3102, May 1995. 89
- 103. [22] Nuha A. S. Alwan, “On the Effect of Tap Length on LMS Adaptive Echo Canceller Performance”, International conference on Computer engineering and Systems, pp. 197-201, November 2006. [23] Sen. M. Kuo and Huan Zhao, “A Real-Time Acoustic Echo Cancellation System”, IEEE International Conference on Systems Engineering, pp. 168-171, August 1990. [24] Andre' H.C. Carezia, Phillip M.S. Burt, Max Gerken, Maria D. Mirandat, Magno T.M. da Silva, “A Stable and Efficient DSP Implementation of A LSL Algorithm for Acoustic Echo Cancelling”, IEEE International Conference on Acoustics, Speech, and Signal Processing, vol.-2, pp. 921-924, May 2001. [25] G. Di Natale, A. Serra, C. Turcotti, “A Board Implementation for Fast APA Acoustic Echo Canceller Using ADSP-21065L DSP”, IEEE International Conference on Automation, Quality Testing and Robotics, vol.2-, pp. 339-344, May 2006. [26] Ali A. Milani, Issa M.S Panahi, Richard Briggs, “Distortion Analysis of Subband Adaptive Filtering Methods for fMRI Active Noise Control Systems”, IEEE Proceedings of the 29th Annual International Conference of the IEEE EMBS Cité Internationale, Lyon, France, pp. 3296-3299, August 2007. [27] Dornean, M. Topa, B.S. Kirei, G. Oltean, “HDL Implementation of the Variable Step Size N-LMS Adaptive Algorithm”, IEEE International conference on Automation, Quality and testing,Robotics, vol.-3, pp. 243-246, May 2008. [28] Satoshi Yamazaki, David K.Asano, “A Serial Unequal Error Protection Code System using Trellis Coded Modulation and an Adaptive Equalizer for Fading Channels”, 14th Asia-Pacific IEEE Conference on Communications, pp. 1-5, October 2008. [29] Gye-Tae Gil, “Normalized LMS Adaptive Cancellation of Self-Image in DirectConversion Receivers”, IEEE Transactions on vehicular technology, vol.- 58, no.- 2, pp. 535-545, February 2009 [30] Sorin Zoican, “A Nonlinear Acoustic Echo Cancellation Scheme Implementation Using the Blackfin Microcomputer”, 9th International IEEE Conference on Telecommunication in Modern Satellite, Cable, and Broadcasting Services, pp. 237240, October 2009. [31] Cristian Anghel, Constantin Paleologu, Jacob Benesty, and Silviu Ciochină, “FPGA Implementation of an Acoustic Echo Canceller Using a VSS-NLMS Algorithm”, International Symposium on Signals, Circuits and Systems, pp. 1-4, July 2009. [32] Sangil Park, “Real-Time Implementation of New Adaptive Detection Structures using the DSP56001”, IEEE International Conference on Systems Engineering, pp. 281-284, August 1989. 90
- 104. [33] Paulo A. C. Lopes, Gonc¸alo Tavares and Jos´e B. Gerald, “A New type of Normalized LMS Algorithm based on The Kalman Filter”, IEEE International Conference on Acoustics, Speech and Signal Processing, pp. 1345-1348, April 2007. [34] John Hakon , “A Circulantly Preconditioned NLMS-type Adaptive Filter”, 17th International Conference Radioelektronika, pp. 1-5, April 2007. [35] Jinhong Wu and Milos Doroslovacki, “A Mean Convergence Analysis for Partial Update NLMS Algorithms”, 41st Annual IEEE Conference on Information Sciences and Systems, pp. 31-34, March 2007. [36] John H˚akon Husøy, Øyvind Lunde Rørtveit, “An NLMS-type Adaptive Filter Using Multiple Fixed Preconditioning Matrices”, International Conference on Signals and Electronic Systems, Kraków, September, 2008. [37] Ch. Renumadhavi, Dr. S.Madhava Kumar, Dr. A. G. Ananth, Nirupama Srinivasan, “A New Approach for Evaluating SNR of ECG Signals and Its Implementation”, Proceedings of the 6th WSEAS International Conference on Simulation, Modelling and Optimization, Lisbon, Portugal, September 2006. [38] Riitta Niemist¨o and Tuomo M¨akel, “On Performance of Linear Adaptive Filtering Algorithms in Acoustic Echo Control in Presence of Distorting Loudspeakers”, International Workshop on Acoustic echo and Noise Control, Kyoto, Japan, September 2003. [39] Cristina Gabriela SĂRĂCIN, Marin SĂRĂCIN, Mihai DASCĂLU, Ana-Maria LEPAR, “Echo Cancellation Using The LMS Algorithm”, U.P.B. Sci. Bull., Series C, vol.- 71, no.- 4, April 2009. [40] Ajay Kr. Singh, G. Singh, D. S. Chauhan, “Implementation of Real Time Programs on the TMSC6713DSK Processor”, International Journal of Signal and Image Processing, vol.- 1, no.-3, pp. 160-168, March 2010. [41] Ali O. Abid Noor, Salina Abdul Samad and Aini Hussain, “Improved, Low Complexity Noise Cancellation Technique for Speech Signals”, World Applied Sciences Journal, vol.- 6, no.-2, pp. 272-278, February 2009. REFERENCE FROM BOOKS & MANUALS: [42] Simon Haykin, “Adaptive Filter Theory”, ISBN 978-0130901262, Prentice Hall, 4th edition, 2001. [43] Paulo S.R. Diniz, “Adaptive Filtering: Algorithms and Practical Implementations”, ISBN 978-0-387-31274-3, Kluwer Academic Publisher © 2008 Springer Science+Business Media, LLC. 91
- 105. [44] Alexander D. Poularikas “Adaptive filtering Primer with MATLAB”, ISBN 978-08493-7043-4, CRC Press, 2006. [45] Donald Reay, “Digital Signal Processing and Applications with the TMS320C6713 and TMS320C6416 DSK”, ISBN 978-0-470-13866-3, John Wiley & Sons, Inc., Edition- 2nd 2008. [46] MathWorks Documentation, “Simulink 6.6 User’s Guide”, March 2007. [47] MathWorks Documentation, “Real-Time Workshop 6.6 User’s Guide” March 2007. [48] MathWorks User’s Guide, “Target Support Package for Use with TI’s C6000™ 4”. [49] Texas Instruments Tutorial, “TMS320C6713 Floating-Point Digital Signal Processor”, (December 2001 – Revised November 2005), SPRS186L [50] Texas Instruments Tutorial, “Code Composer Studio Development Tools v3.3 Getting Started Guide”, (Oct 2006), SPRU509H [51] Texas Instruments Tutorial, “TMS320C6000 Instruction Set Simulator Technical Reference Manual”, (April 2007), SPRS600I [52] Texas Instruments Tutorial, “How to Begin Development Today With the TMS320C6713 Floating-Point DSP”, (October 2002), SPRA809A [53] Texas Instruments Tutorial, “TMS320C6713 Hardware Designers Resource Guide”, (July 2004), SPRAA33 92
- 106. APPENDIX-I LIST OF PUBLICATIONS International/ National Journals (Published/Accepted) [1] Raj kumar Thenua and S.K. Agarwal, “Simulation and Performance Analysis of Adaptive Filter in Noise Cancellation”, International Journal of Engineering Science and Technology (IJEST), ISSN: 0975-5462, Vol. 2(9), 2010, Page no. 4374-4379. (Published) International/ National Conferences (Published/Accepted) [2] Raj kumar Thenua and S.K. Agarwal, “Hardware Implementation of Adaptive algorithms for Noise Cancellation”, IEEE International Conference on Network Communication and Computer (ICNCC 2011), 21st -23rd Mar 2011, organized by International Association of Computer Science and Information Technology (IACSIT) and Singapore Institute of Electronics (SIE) at New Delhi, India. (Published) [3] Raj kumar Thenua, S.K. Agarwal and Mohd. Ayub khan, “Performance analyses of Adaptive Noise Canceller for an ECG signal” International Conference on Recent Trends in Engineering, Technology and Management on 26th -27th Feb 2011 at BIET, Jhansi, India. (Published) [4] Raj kumar Thenua and S.K. Agarwal, “Hardware Implementation of NLMS Algorithm for Adaptive Noise Cancellation”, National Conference on Electronics and Communication (NCEC-2010) on 22nd -24th December 2010 at MITS, Gwalior. (Published) [5] Raj kumar Thenua and S.K. Agarwal, “Real-time Noise Cancellation using Digital Signal Processor”, National conference on Electronics, Computers and Communications (NCECC-2010) on 06th -07th March 2010 at MITS, Gwalior. (Published) 93
- 107. APPENDIX-II MATLAB COMMANDS load Load workspace variables from disk randn Normally distributed random numbers fir1 Window-based finite impulse response filter design filter 1-D digital filter zeros Create array of all zeros dot Vector dot product mean Average or mean value of array sum Sum of array elements abs Absolute value and complex magnitude eye Identity matrix hold Retain current graph in figure disp Display text or array simulink Open Simulink block library wavwrite Writes data to 8-, 16-, 24-, and 32-bit .wav files csvread Read comma-separated value file ccsboardinfo Information about boards and simulators known to CCS IDE ccsdsp Create link to CCS IDE enable Enable RTDX interface, specified channel, or all RTDX channels 94















![Chapter-1
INTRODUCTION
In the process of transmission of information from the source to receiver, noise from
the surroundings automatically gets added to the signal. The noisy signal contains two
components, one carries the information of interest i.e. the useful signal; the other consists of
random errors or noise which is superimposed on the useful signal. These random errors or
noise are unwanted because they diminish the accuracy and precision of the measured signal.
Therefore the effective removal or reduction of noise in the field of signal processing is an
active area of research.
1.1
Overview
The use of adaptive filter [1] is one of the most popular proposed solutions to reduce
the signal corruption caused by predictable and unpredictable noise. An adaptive filter has
the property of self-modifying its frequency response to change its behavior with time. It
allows the filter to adapt to the response as the input signal characteristics change. Due to this
capability and the construction flexibility, the adaptive filters have been employed in many
different applications like telephonic echo cancellation, radar signal processing, navigation
systems, communications, channel equalization, bio-medical & biometric signal processing
etc.
In the field of adaptive filtering, there are mainly two algorithms that are used to force
the filter to adapt its coefficients – Stochastic gradient based algorithm and Recursive Least
Square based algorithm. Their implementations and adaptation properties are the determining
factors for choice of application. The main requirements and the performance parameters for
adaptive filters are the convergence speed and the asymptotic error. The convergence speed is
the primary property of an adaptive filter which enables one to measure how quickly the filter
is converging to the desired value. It is a major requirement as well as a limiting factor for
most of the applications of adaptive filters.
The asymptotic error represents the amount of error that the filter introduces at steady
state after it has converged to the desired value. The RLS filters due to their computational
structure have considerably better properties than the LMS filters both in terms of the
2](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-15-320.jpg)
![convergence speed and the asymptotic error. The RLS filters which outperform the LMS
filters obtain their solution for the weight updated directly from the Mean Square Error
(MSE) [2]. However, they are computationally very demanding and also very dependent
upon the precision of the input signal. Their computational requirements are significant and
imply the use of expensive and power demanding high-speed processors. Also, for the
systems lacking the appropriate dynamic range, the adaptation algorithms can become
unstable. In this manner to match the computational requirements a DSP processor can be a
better substitute.
1.2
Motivation
In the field of signal processing there is a significant need of a special class of digital
filters known as adaptive filters. Adaptive filters are used commonly in many different
configurations for different applications. These filters have various advantages over the
standard digital filters. They can adapt their filter coefficients from the environment
according to preset rules. The filters are capable of learning from the statistics of current
conditions and change their coefficients in order to achieve a certain goal. In order to design a
filter prior knowledge of the desired response is required. When such knowledge is not
available due to the changing nature of the filter’s requirements, it is impossible to design a
standard digital filter. In such situations, adaptive filters are desirable.
The algorithms used to perform the adaptation and the configuration of the filter
depends directly on the application of the filter. However, the basic computational engine that
performs the adaptation of the filter coefficients can be the same for different algorithms and
it is based on the statistics of the input signals to the system. The two classes of adaptive
filtering algorithms namely Recursive Least Squares (RLS) and Least Mean Squared (LMS)
are capable of performing the adaptation of the filter coefficients.
When we talk about a real scenario where the information generated from the source
side gets contaminated by the noise signal, this situation demands for the adaptive filtering
algorithm which provides fast convergence while being numerically stable without
incorporating much memory.
3](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-16-320.jpg)
![Hence, the motivation for the thesis is to search for an adaptive algorithm which has
reduced computational complexity, reasonable convergence speed and good stability without
degrading the performance of the adaptive filter and then realize the algorithm on an efficient
hardware which makes it more practical in real time applications.
1.3
Scope of the Work
In numerous application areas, including biomedical engineering, radar & sonar
engineering, digital communications etc., the goal is to extract the useful signal corrupted by
interferences and noises. In this wok an adaptive noise canceller will be designed that will
more effective than available ones. To achieve an effective adaptive noise canceller, the
simulation of various adaptive algorithms will be done on MATLAB. The obtained suitable
algorithm will be implemented on the TMS320C6713 DSK hardware. The designed system
will be tested for the filtering of a noisy ECG signal and tone signal and the system
performance will be compared with the early designed available systems. The designed
system may be useful for cancelling of interference in ECG signal, periodic interference in
audio signal and broad-band interference in the side-lobes of an antenna array.
In this work for the simulation, MATLAB version 7.4.0.287(R2007a) is used, though
Labview version7 may also be applicable. For the hardware implementation, Texas
Instrument (TI) TMS320C6713 digital signal processor is used. However, Field
Programmable Gate Array (FPGA) may also be suitable. To assist the hardware
implementation Simulink version 6.6 is appropriate to generate C code for the DSP hardware.
To communicate with DSP processor, Integrated Development Environment (IDE) software
Code Composer Studio V3.1 is essential. Function generator and noise generator or any other
audio device can be used as an input source for signal analysis. For the analysis of output data
DSO is essentially required however CRO may also be used.
Current adaptive noise cancellation models [5], [9], [11] works on relatively low
processing speed that is not suitable for real-time signals which results delay in output. In this
direction, to increase the processing speed and to improve signal-to-noise ratio, a DSP
processor can be useful because it is a fast special purpose microprocessor with a specialized
type of architecture and an appropriate instruction set for signal processing. It is also well
suited for numerically intensive calculations.
4](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-17-320.jpg)


![Chapter-2
LITERATURE SURVEY
In the last thirty years significant contributions have been made in the field of signal
processing. The advances in digital circuit design have been the key technological
development that sparked a growing interest in the field of digital signal processing. The
resulting digital signal processing systems are attractive due to their low cost, reliability,
accuracy, small physical sizes and flexibility.
In numerous applications of signal processing, communications and biomedical we
face the necessity to remove noise and distortion from the signals. These phenomena are due
to time-varying physical processes which are unknown sometimes. One of these situations is
during the transmission of a signal from one point to another. The channel which may be of
wires, fibers, microwave beam etc., introduces noise and distortion due to the variations of its
properties. These variations may be slow or fast. Since most of the time the variations are
unknown, so there is a requirement of such type of filters that can work effectively in such
unknown environment. The adaptive filter is the right choice that diminishes and sometimes
completely eliminates the signal distortion.
The most common adaptive filters which are used during the adaption process are the
finite impulse response (FIR) types. These are preferable because they are stable, and no
special adjustments are needed for their implementation. In adaptive filters, the filter weights
are needed to be updated continuously according to certain rules. These rules are presented in
form of algorithms. There are mainly two types of algorithms that are used for adaptive
filtering. The first is stochastic gradient based algorithm known as Least Mean Squared
(LMS) algorithm and second is based on least square estimation which is known as Recursive
Least Square (RLS) algorithm. A great deal of research [1]-[5], [14], [15] has been carried
out in subsequent years for finding new variant of these algorithms to achieve better
performance in noise cancellation applications.
Bernard Widrow et. al.[1] in 1975, described the adaptive noise cancelling as an
alternative method of estimating signals which are corrupted by additive noise or interference
by employing LMS algorithm. The method uses a “primary” input containing the corrupted
signal and a “reference” input containing noise correlated in some unknown way with the
7](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-20-320.jpg)
![primary noise. The reference input is adaptively filtered and subtracted from the primary
input to obtain the signal estimate. Widrow [1] focused on the usefulness of the adaptive
noise cancellation technique in a variety of practical applications that included the cancelling
of various forms of periodic interference in electrocardiography, the cancelling of periodic
interference in speech signals, and the cancelling of broad-band interference in the side-lobes
of an antenna array.
In 1988, Ahmed S. Abutaleb [2] introduced a new principle- Pontryagin minimum
principal to reduce the computational time of LMS algorithm. The proposed method reduces
the computation time drastically without degrading the accuracy of the system. When
compared to the LMS-based widrow [1] model, it was shown to have superior performance.
The LMS based algorithms are simple and easy to implement but the convergence speed is
slow. Abhishek Tandon et. al.[3] introduced an efficient, low-complexity Normalized least
mean squared (NLMS) algorithm for echo cancellation in multiple audio channels. The
performance of the proposed algorithm was compared with other adaptive algorithms for
acoustic echo cancellation. It was shown that the proposed algorithm has reduced complexity,
while providing a good overall performance.
In NLMS algorithm, all the filter coefficients are updated for each input sample. Dong
Hang et. al.[4] presented a multi-rate algorithm which can dynamically change the update
rate of the coefficients of filter by analyzing the actual application environment. When the
environment is varying, the rate increases while it decreases when the environment is stable.
The results of noise cancellation indicate that the new method has faster convergence speed,
low computation complexity, and the same minimum error as the traditional method.
Ying He et. al.[5] presented the MATLAB simulation of RLS algorithm and the
performance was compared with LMS algorithm. The convergence speed of RLS algorithm
is much faster and produces a minimum mean squared error (MSE) among all available LMS
based algorithms but at the cost of increased computational complexity which makes its
implementation difficult on hardware.
Nowadays the availability of high speed digital signal processors has attracted the
attention of the research scholars towards the real-time implementation of the available
algorithms on the hardware platform. Digital signal processors are fast special-purpose
8](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-21-320.jpg)
![microprocessors with a specialized type of architecture and an instruction set appropriate for
signal processing. The architecture of the digital signal processor is very well suited for
numerically intensive calculations. DSP techniques have been very successful because of the
development of low-cost software and hardware support. DSP processors are concerned
primarily with real-time signal processing.
DSP processors exploit the advantages of
microprocessors. They are easy to use, flexible, economical and can be reprogrammed easily.
The starting of real-time hardware implementation was done by Edgar Andrei [6]
initially on the Motorola DSP56307 in 2000. Later in year 2002, Michail D. Galanis et. al.[7]
presented a DSP course for real-time systems design and implementation based on the
TMS320C6211. This course emphasized the issue of transition from an advanced design and
simulation environment like MATLAB to a DSP software environment like Code Composer
Studio.
Boo-Shik Ryu et. al.[8] implemented and investigated the performance of a noise
canceller with DSP processor (TMS320C6713) using the LMS algorithm, NLMS algorithm
and VSS-NLMS algorithm. Results showed that the proposed combination of hardware and
VSS-NLMS algorithm has not only a faster convergence rate but also lower distortion when
compared with the fixed step size LMS algorithm and NLMS algorithm in real time
environments.
In 2009, J. Gerardo Avalos et. al. [9] have done an implementation of a digital
adaptive filter on the digital signal processor TMS320C6713 using a variant of the LMS
algorithm which consists of error codification. The speed of convergence is increased and the
complexity of design for its implementation in digital adaptive filters is reduced because the
resulting codified error is composed of integer values. The LMS algorithm with codified error
(ECLMS) was tested in an environmental noise canceller and the results demonstrate an
increase in the convergence speed and a reduction of processing time.
C.A. Duran et. al. [10] presented an implementation of the LMS, NLMS and other
LMS based algorithms on the DSK TMS320C6713 with the intention to compare their
performance, analyze their time & frequency behavior along with the processing speed of the
algorithms. The objective of the NLMS algorithm is to obtain the best convergence factor
considering the input signal power in order to improve the filter convergence time. The
9](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-22-320.jpg)
![obtained results show that the NLMS has better performance than the LMS. Unfortunately,
the computational complexity increases which means more processing time.
The work related to real-time implementation so far discussed was implemented on
DSP processor by writing either assembly or C program directly in the editor of Code
Composer Studio (CCS). The writing of assembly program needs so many efforts therefore
only professional person can do this similarly C programming are not simple as far as
hardware implementation concerned.
There is a simple way to create C code automatically which requires less effort and is
more efficient. Presently only few researchers [11]-[13] are aware about this facility which is
provided by the MATLAB Version 7.1 and higher versions, using embedded target Real-time
Workshop (RTW). Gaurav Saxena et. al. [11] have used this auto code generation facility
and presented better results than the conventional C code writing.
Gaurav Saxena et. al. [11] discussed the real time implementation of adaptive noise
cancellation based on an improved adaptive wiener filter on Texas Instruments
TMS320C6713 DSK. Then its performance was compared with the Lee’s adaptive wiener
filter. Furthermore, a model based design of adaptive noise cancellation based on LMS filter
using simulink was implemented on TI C6713. The auto-code generated by the Real Time
Workshop for the simulink model of LMS filter was compared with the ‘C’ implementation
of LMS filter on C6713 in terms of code length and computation time. It was found to have a
large improvement in computation time but at the cost of increased code length.
S.K. Daruwalla et. al. [12] focused on the development and the real time
implementation of various audio effects using simulink blocks by employing an audio signal
as input. This system has helped the sound engineers to easily configure/capture various
audio effects in advance by simply varying the values of predefined simulink blocks. The
digital signal processor is used to implement the designs; this broadens the versatility of
system by allowing the user to employ the processor for any audio input in real-time. The
work is enriched with the real-time concepts of controlling the various audio effects via onboard DIP switches on the C6713 DSK.
10](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-23-320.jpg)
![In Nov-2009, Yaghoub Mollaei [13] designed an adaptive FIR filter with normalized
LMS algorithm to cancel the noise. A simulink model is created and linked to TMS320C6711
digital signal processor through embedded target for C6000 SIMULINK toolbox and realtime workshop to perform hardware adaptive noise cancellation. Three noises with different
powers were used to test and judge the system performance in software and hardware. The
background noises for speech and music track were eliminated adequately with reasonable
rate for all the tested noises.
The outcomes of the literature survey can be summarized as follows:
The adaptive filters are attractive to work in an unknown environment and are suitable
for noise cancellation applications in the field of digital signal processing.
To update the adaptive filter weights two types of algorithms, LMS & RLS are used.
RLS based algorithms have better performance but at the cost of larger computational
complexity therefore very less work [5], [15] is going on in this direction. On the
other hand, LMS based algorithms are simple to implement and its few variants like
NLMS have comparable performance with RLS algorithm. So a large amount of
research [1]-[5] through simulation has been carried out in this regard to improve the
performance of LMS based algorithms.
Simulation can be carried out on non-real time signals only. Therefore for real-time
application there is a need of the hardware implementation of LMS based algorithms.
The DSP processor has been found to be a suitable hardware for signal processing
applications.
Hence, there is a requirement to find out the easiest way for the hardware
implementation of adaptive filter algorithms on a particular DSP processor. The use
of simulink model [11]-[13] with embedded target and real time workshop has proved
to be helpful for the same.
Therefore the simulink based hardware implementation of NLMS algorithm for ECG
signal analysis can be a good contribution in the field of adaptive filtering.
11](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-24-320.jpg)
![Chapter-3
ADAPTIVE FILTERS
3.1
Introduction
Filtering is a signal processing operation. Its objective is to process a signal in order to
manipulate the information contained in the signal. In other words, a filter is a device that
maps its input signal to another output signal facilitating the extraction of the desired
information contained in the input signal. A digital filter is the one that processes discretetime signals represented in digital format. For time-invariant filters the internal parameters
and the structure of the filter are fixed, and if the filter is linear the output signal is a linear
function of the input signal. Once the prescribed specifications are given, the design of timeinvariant linear filters entails three basic steps namely; the approximation of the
specifications by a rational transfer function, the choice of an appropriate structure defining
the algorithm, and the choice of the form of implementation for the algorithm.
An adaptive filter [1], [2] is required when either the fixed specifications are unknown
or the specifications cannot be satisfied by time-invariant filters. Strictly speaking, an
adaptive filter is a nonlinear filter since its characteristics are dependent on the input signal
and consequently the homogeneity and additivity conditions are not satisfied. However, if we
freeze the filter parameters at a given instant of time, most adaptive filters are linear in the
sense that their output signals are linear functions of their input signals.
The adaptive filters are time-varying since their parameters are continuously changing
in order to meet a performance requirement. In this sense, we can interpret an adaptive filter
as a filter that performs the approximation step on-line. Usually, the definition of the
performance criterion requires the existence of a reference signal that is usually hidden in the
approximation step of fixed-filter design.
Adaptive filters are considered nonlinear systems; therefore their behaviour analysis is
more complicated than for fixed filters. On the other hand, since the adaptive filters are self
designing filters from the practitioner’s point of view, their design can be considered less
involved than the digital filters with fixed coefficients.
12](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-25-320.jpg)
![Adaptive filters work on the principle of minimizing the mean squared difference
(or error) between the filter output and a target (or desired) signal. Adaptive filters are used
for estimation of non-stationary signals and systems, or in applications where a sample-by
sample adaptation of a process and a low processing delay is required.
Adaptive filters are used in applications [26]-[29] that involve a combination of three
broad signal processing problems:
(1) De-noising and channel equalization – filtering a time-varying noisy signal to remove the
effect of noise and channel distortions.
(2) Trajectory estimation – tracking and prediction of the trajectory of a non stationary signal
or parameter observed in noise.
(3) System identification – adaptive estimation of the parameters of a time-varying system
from a related observation.
Adaptive linear filters work on the principle that the desired signal or parameters can
be extracted from the input through a filtering or estimation operation. The adaptation of the
filter parameters is based on minimizing the mean squared error between the filter output and
a target (or desired) signal. The use of the Least Square Estimation (LSE) criterion is
equivalent to the principal of orthogonality in which at any discrete time m the estimator is
expected to use all the available information such that any estimation error at time m is
orthogonal to all the information available up to time m.
3.1.1 Adaptive Filter Configuration
The general set up of an adaptive-filtering environment is illustrated in Fig.3.1 [43],
where n is the iteration number, x(n) denotes the input signal, y(n) is the adaptive-filter output
signal, and d(n) defines the desired signal. The error signal e (n) is calculated as d (n) – y (n).
The error signal is then used to form a performance function that is required by the adaptation
algorithm in order to determine the appropriate updating of the filter coefficients. The
minimization of the objective function implies that the adaptive-filter output signal is
matching the desired signal in some sense. At each sampling time, an adaptation algorithm
adjusts the filter coefficients w(n) =[w0(n)w1(n)….. wN−1(n)] to minimize the difference
between the filter output and a desired or target signal.
13](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-26-320.jpg)

![yields a quadratic mean-square error (MSE = E[|e(n)|2]) function with a unique
optimal solution. Other alternative adaptive FIR realizations are also used in order to
obtain improvements as compared to the transversal filter structure, in terms of
computational complexity, speed of convergence and finite word-length properties.
Adaptive IIR filter realizations: The most widely used realization of adaptive IIR
filters is the canonic direct form realization [42], due to its simple implementation and
analysis. However, there are some inherent problems related to recursive adaptive
filters which are structure dependent such as pole-stability monitoring requirement
and slow speed of convergence. To address these problems, different realizations
were proposed attempting to overcome the limitations of the direct form structure.
(c) Algorithm: The algorithm is the procedure used to adjust the adaptive filter
coefficients in order to minimize a prescribed criterion. The algorithm is determined by
defining the search method (or minimization algorithm), the objective function and the nature
of error signal. The choice of the algorithm determines several crucial aspects of the overall
adaptive process, such as existence of sub-optimal solutions, biased optimal solution and
computational complexity.
x(n)
w0
Z‐1
⊗
x(n-1)
w1
Z-1
Z-1
⊗
wN-1
⊕
y(n)
⊕
_
e(n)
d(n)
+
Fig.3.2. Transversal FIR filter architecture
15
x(n-N+1)
⊗](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-28-320.jpg)
![3.1.2 Adaptive Noise Canceller (ANC)
The goal of adaptive noise cancellation system is to reduce the noise portion and to
obtain the uncorrupted desired signal. In order to achieve this task, a reference of the noise
signal is needed. That reference is fed to the system, and it is called a reference signal x(n).
However, the reference signal is typically not the same signal as the noise portion of the
primary signal; it can vary in amplitude, phase or time. Therefore, the reference signal cannot
be simply subtracted from the primary signal to obtain the desired portion at the output.
Signal
Source
Noise
Source
s(n)
Primary Input
d(n)
x1(n)
Reference Input
x(n)
Adaptive
Filter
+
Σ
e(n)
Output
_
y(n)
Adaptive Noise Canceller
Fig.3.3. Block diagram for Adaptive Noise Canceller
Consider the Adaptive Noise Canceller (ANC) shown in Fig.3.3 [1]. The ANC has
two inputs: the primary input d(n), which represents the desired signal corrupted with
undesired noise and the reference input x(n), which is the undesired noise to be filtered out of
the system. The primary input therefore comprises of two portions: - first, the desired signal
and the other one is noise signal corrupting the desired portion of the primary signal.
The basic idea for the adaptive filter is to predict the amount of noise in the primary
signal and then subtract that noise from it. The prediction is based on filtering the reference
signal x(n), which contains a solid reference of the noise present in the primary signal. The
noise in the reference signal is filtered to compensate for the amplitude, phase and time delay
and then subtracted from the primary signal. The filtered noise represented by y(n) is the
system’s prediction of the noise portion of the primary signal and is subtracted from desired
signal d(n) resulting in a signal called error signal e(n), and it presents the output of the
system. Ideally, the resulting error signal should be only the desired portion of the primary
signal.
16](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-29-320.jpg)

![As noted above, the filter produces estimate of the noise in the primary signal
adjusted for magnitude, phase and time delay. This estimate is then subtracted from the noise
corrupted primary signal to obtain the desired signal. For the filter to work well, the adaptive
algorithm has to adjust the filter coefficients such that output of the filter is a good estimate
of the noise present in the primary signal.
To determine the amount by which noise in the primary signal is reduced, the mean
squared error technique is used. The Minimum Mean Squared Error (MMSE) is defined as
[42]:
min E[d (n) − XW T ] 2 = min E[(d (n) − y (n)) 2 ]
(3.1)
where d is the desired signal, X and W are the vectors of the input reference signal and
the filter coefficients respectively. This represents the measure of how well the newly
constructed filter (given as a convolution product y(n) = XW) estimates the noise present in
the primary signal. The goal is to reduce this error to a minimum. Therefore, the algorithms
that perform adaptive noise cancellation are constantly searching for a coefficient vector W,
which produces the minimum mean squared error.
Minimizing the mean squared of the error signal minimizes the noise portion of the
primary signal but not the desired portion. To understand this principle, recall that the
primary signal is made of the desired portion and the noise portion. The filtered reference
signal y(n) is a reference of the noise portion of the primary signal and therefore is correlated
with it. However, the reference signal is not correlated with the desired portion of the primary
signal. Therefore, minimizing the mean squared of the error signal minimizes only the noise
in the primary signal. This principle can be mathematically described as follows:
If we denote the desired portion of primary signal with s(n), and the noise portion of
desired signal as x1(n), it follows that d(n) = s(n) + x1(n). As shown in Fig.3.3, the output of
the system can be written as [43]:
e(n) = d (n) − y (n)
(3.2)
e ( n ) = s ( n ) + x1 ( n ) − y ( n )
e(n) 2 = s (n) 2 + (( x1 (n) − y (n)) 2 + 2 s (n)(( x1 (n) − y (n))
E[e(n) 2 ] = E[ s (n) 2 ] + (( x1 (n) − y (n)) 2 + 2 s (n)(( x1 (n) − y (n))
18](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-31-320.jpg)
![E[e(n) 2 ] = E[ s (n) 2 ] + E[(( x1 (n) − y (n)) 2 ] + 2 E[ s (n)(( x1 (n) − y (n))]
(3.3)
Due to the fact that the s(n) is un-correlated to both x1(n) and y(n), as noted earlier, the
last term is equal to zero, so we have
E[e(n) 2 ] = E[ s (n) 2 ] + E[(( x1 (n) − y (n)) 2 ]
min E[e(n) 2 ] = min E[ s(n) 2 ] + min E[(( x1 (n) − y (n))2 ]
(3.4)
and since s(n) is independent of W, we have
min E[e(n) 2 ] = E[ s (n) 2 ] + min E[(( x1 (n) − y (n)) 2 ]
(3.5)
Therefore, minimizing the error signal, minimizes the mean squared of the difference
between the noise portion of the primary signal x1(n), and the filter output y(n) .
3.2
Approaches to Adaptive Filtering Algorithms
Basically two approaches can be defined for deriving the recursive formula for the
operation of Adaptive Filters. They are as follows:
(i) Stochastic Gradient Approach: In this approach to develop a recursive algorithm for
updating the tap weights of the adaptive transversal filter, the process is carried out in two
stages. First we use an iterative procedure to find the optimum Wiener solution [43]. The
iterative procedure is based on the method of steepest descent. This method requires the
use of a gradient vector, the value of which depends on two parameters: the correlation
matrix of the tap inputs in the transversal filter and the cross-correlation vector between
the desired response and the same tap inputs. Secondly, instantaneous values for these
correlations are used to derive an estimate for the gradient vector. Least Mean Squared
(LMS) and Normalized Least Mean Squared (NLMS) algorithms lie under this approach
and are discussed in subsequent sections.
(ii) Least Square Estimation: This approach is based on the method of least squares.
According to this method, a cost function is minimized that is defined as the sum of
weighted error squares, where the error is the difference between some desired response
and actual filter output. This method is formulated with block estimation in mind. In
block estimation, the input data stream is arranged in the form of blocks of equal length
(duration) and the filtering of input data proceeds on a block by block basis, which
requires a large memory for computation. The Recursive Least Square (RLS) algorithm
19](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-32-320.jpg)
![falls under this approach and is discussed in subsequent section.
3.2.1
Least Mean Square (LMS) Algorithm
The Least Mean Square (LMS) algorithm [1] was first developed by Widrow and
Hoff in 1959 through their studies of pattern recognition [42]. Thereon it has become one of
the most widely used algorithm in adaptive filtering. The LMS algorithm is a type of adaptive
filter known as stochastic gradient-based algorithm as it utilizes the gradient vector of the
filter tap weights to converge on the optimal wiener solution. It is well known and widely
used due to its computational simplicity. With each iteration of the LMS algorithm, the filter
tap weights of the adaptive filter are updated according to the following formula:
w( n + 1) = w( n) + 2 μe( n ) x ( n)
(3.6)
where x(n) is the input vector of time delayed input values, and is given by
x(n) = [ x(n) x(n − 1) x(n − 2)....x(n − N + 1)]T
(3.7)
w( n) = [ w0 ( n) w1 ( n) w2 ( n)....w N −1 (n)]T represents the coefficients of the adaptive FIR
filter tap weight vector at time n and μ is known as the step size parameter and is a small
positive constant.
The step size parameter controls the influence of the updating factor. Selection of a
suitable value for μ is imperative to the performance of the LMS algorithm. If the value of μ
is too small, the time an adaptive filter takes to converge on the optimal solution will be too
long; if the value of μ is too large the adaptive filter becomes unstable and its output diverges
[14], [15], [22].
3.2.1.1 Derivation of the LMS Algorithm
The derivation of the LMS algorithm builds upon the theory of the wiener solution for
the optimal filter tap weights, w0, as outlined above. It also depends on the steepest descent
algorithm that gives a formula which updates the filter coefficients using the current tap
weight vector and the current gradient of the cost function with respect to the filter tap weight
coefficient vector, ξ(n).
w(n + 1) = w(n) − μ∇ξ ( n)
(3.8)
20](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-33-320.jpg)
![where
ξ (n) = E[e 2 (n)]
(3.9)
As the negative gradient vector points in the direction of steepest descent for the N
dimensional quadratic cost function each recursion shifts the value of the filter coefficients
closer towards their optimum value which corresponds to the minimum achievable value of
the cost function, ξ(n). The LMS algorithm is a random process implementation of the
steepest descent algorithm, from Eq. (3.9). Here the expectation for the error signal is not
known so the instantaneous value is used as an estimate. The gradient of the cost function,
ξ(n) can alternatively be expressed in the following form:
∇ξ (n) = ∇(e 2 (n))
= ∂e 2 (n) / ∂w
= 2e(n)∂e(n) / ∂w
= 2e( n)∂[d ( n) − y ( n)] / ∂w
= −2e(n)∂ewT (n).x(n)] / ∂w
= −2 e ( n ) x ( n )
(3.10)
Substituting this into the steepest descent algorithm of Eq. (3.9), we arrive at the
recursion for the LMS adaptive algorithm.
w( n + 1) = w( n) + 2 μe( n) x ( n)
(3.11)
3.2.1.2 Implementation of the LMS Algorithm
For the Implementation of each iteration of the LMS algorithm requires three distinct
steps in the following order:
1. The output of the FIR filter, y(n) is calculated using Eq. (3.12).
N −1
y (n) = ∑ w( n)x(n − i ) = wT (n) x(n)
(3.12)
i =0
2. The value of the error estimation is calculated using Eq. (3.13).
21](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-34-320.jpg)
![e( n ) = d ( n ) − y ( n )
(3.13)
3. The tap weights of the FIR vector are updated in preparation for the next iteration, by
Eq. (3.14).
w( n + 1) = w( n) + 2 μe( n) x ( n)
(3.14)
The main reason for the popularity of LMS algorithms in adaptive filtering is its
computational simplicity that makes its implementation easier than all other commonly used
adaptive algorithms. For each iteration, the LMS algorithm requires 2N additions and 2N+1
multiplications (N for calculating the output, y(n), one for 2μe(n) and an additional N for the
scalar by vector multiplication) .
3.2.2
Normalized Least Mean Square (NLMS) Algorithm
In the standard LMS algorithm when the convergence factor μ is large, the algorithm
experiences a gradient noise amplification problem. In order to solve this difficulty we can
use the NLMS algorithm [14]-[17]. The correction applied to the weight vector w(n) at
iteration n+1 is “normalized” with respect to the squared Euclidian norm of the input vector
x(n) at iteration n. We may view the NLMS algorithm as a time-varying step-size algorithm,
calculating the convergence factor μ as in Eq. (3.15)[10].
μ ( n) =
α
c + x ( n)
(3.15)
2
where α is the NLMS adaption constant, which optimize the convergence rate of the
algorithm and should satisfy the condition 0<α<2, and c is the constant term for
normalization and is always less than 1.
The Filter weights are updated by the Eq. (3.16).
w(n + 1) = w(n) +
α
c + x ( n)
2
e( n ) x ( n )
(3.16)
It is important to note that given an input data (at time n) represented by the input
vector x(n) and desired response d(n), the NLMS algorithm updates the weight vector in such
a way that the value w(n+1) computed at time n+1 exhibits the minimum change with respect
22](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-35-320.jpg)
![to the known value w(n) at time n. Hence, the NLMS is a manifestation of the principle of
minimum disturbance [3].
3.2.2.1 Derivation of the NLMS Algorithm
This derivation of the normalized least mean square algorithm is based on FarhangBoroujeny and Diniz [43]. To derive the NLMS algorithm we consider the standard LMS
recursion in which we select a variable step size parameter, μ(n). This parameter is selected
so that the error value, e+(n), will be minimized using the updated filter tap weights, w(n+1),
and the current input vector, x(n).
w(n + 1) = w(n) + 2 μ (n)e(n) x(n)
e + (n) = d (n) − wT (n + 1) x(n)
= (1 − 2 μ (n) xT (n) x(n))e(n)
(3.17)
Next we minimize (e+(n))2, with respect to μ(n). Using this we can then find a value
for µ(n) which forces e+(n) to zero.
μ ( n) =
1
2 x ( n ) x ( n)
(3.18)
T
This μ(n) is then substituted into the standard LMS recursion replacing μ, resulting in
the following.
w(n + 1) = w(n) + 2 μ (n)e(n) x(n)
1
w(n + 1) = w(n) + T
e( n) x ( n)
x ( n) x ( n)
w(n + 1) = w(n ) + μ (n) x(n )
(3.19)
, where μ (n) =
α
x x+c
T
(3.20)
Often the NLMS algorithm as expressed in Eq. (3.20 is a slight modification of the
standard NLMS algorithm detailed above. Here the value of c is a small positive constant in
order to avoid division by zero when the values of the input vector are zero. This was not
implemented in the real time as in practice the input signal is never allowed to reach zero due
to noise from the microphone and from the ADC on the Texas Instruments DSK. The
parameter α is a constant step size value used to alter the convergence rate of the NLMS
algorithm, it is within the range of 0<α<2, usually being equal to 1.
23](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-36-320.jpg)
![3.2.2.2 Implementation of the NLMS Algorithm
The NLMS algorithm is implemented in MATLAB as outlined later in Chapter 6. It is
essentially an improvement over LMS algorithm with the added calculation of step size
parameter for each iteration.
1. The output of the adaptive filter is calculated as:
N −1
y (n) = ∑ w( n)x(n − i ) = wT (n) x(n)
(3.21)
i =0
2. The error signal is calculated as the difference between the desired output and the filter
output given by:
e( n) = d ( n ) − y ( n)
(3.22)
3. The step size and filter tap weight vectors are updated using the following equations in
preparation for the next iteration:
For i=0,1,2,…….N-1
μ i ( n) =
α
c + xi ( n )
(3.23)
2
w(n + 1) = w(n) + μ i (n)e(n) xi (n)
(3.24)
where α is the NLMS adaption constant and c is the constant term for normalization.
With α =0.02 and c=0.001, each iteration of the NLMS algorithm requires 3N+1
multiplication operations.
3.2.3
Recursive Least Square (RLS) Algorithm
The other class of adaptive filtering technique studied in this thesis is known as
Recursive Least Squares (RLS) algorithm [42]-[44]. This algorithm attempts to minimize the
cost function in Eq. (3.25) where k=1 is the time at which the RLS algorithm commences and
λ is a small positive constant very close to, but smaller than 1. With values of λ<1, more
importance is given to the most recent error estimates and thus the more recent input samples,
that results in a scheme which emphasizes on recent samples of observed data and tends to
forget the past values.
24](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-37-320.jpg)
![n
2
ξ ( n) = ∑ λ n − k e n ( k )
(3.25)
k =1
Unlike the LMS algorithm and NLMS algorithm, the RLS algorithm directly
considers the values of previous error estimations. RLS algorithm is known for excellent
performance when working in time varying environments. These advantages come at the cost
of an increased computational complexity and some stability problems.
3.2.3.1 Derivation of the RLS Algorithm
The RLS cost function of Eq. (3.25) shows that at time n, all previous values of the
estimation error since the commencement of the RLS algorithm are required. Clearly, as time
progresses the amount of data required to process this algorithm increases. Limited memory
and computation capabilities make the RLS algorithm a practical impossibility in its purest
form. However, the derivation still assumes that all data values are processed. In practice
only a finite number of previous values are considered, this number corresponds to the order
of the RLS FIR filter, N.
First we define yn(k) as the output of the FIR filter, at n, using the current tap weight
vector and the input vector of a previous time k. The estimation error value en(k) is the
difference between the desired output value at time k and the corresponding value of yn(k).
These and other appropriate definitions are expressed below, for k=1,2, 3,., n.
yn (k ) = wT (n) x(k )
en (k ) = d (k ) − yn (k )
d (n) = [d (1), d (2).....d (n)]T
y (n) = [ yn (1), yn (2)..... yn (n)]T
e(n) = [en (1), en (2).....en (n)]T
e( n ) = d ( n ) − y ( n )
(3.26)
If we define X(n) as the matrix consisting of the n previous input column vector up to
the present time then y(n) can also be expressed as Eq. (3.27).
X (n) = [ x(1), x(2),....... x( n)]
y (n) = X T (n) w(n)
(3.27)
25](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-38-320.jpg)


![2. The intermediate gain vector is calculated using Eq. (3.34).
−1
u (n) = wλ (n − 1) x(n)
k (n) = u (n) /(λ + x T (n)u (n))
(3.34)
3. The estimation error value is calculated using Eq. (3.35).
en −1 (n) = d (n) − yn −1 (n)
(3.35)
4. The filter tap weight vector is updated using Eq. (3.36) and the gain vector calculated
in Eq. (3.34).
w(n) = w T (n − 1) + k (n)en −1 (n)
(3.36)
5. The inverse matrix is calculated using Eq. (3.37).
ψ λ −1 ( n) = λ −1 (ψ λ −1 ( n − 1) − k ( n)[ x T ( n)ψ λ −1 ( n − 1)]
(3.37)
When we calculate for each iteration of the RLS algorithm, it requires 4N2
multiplication and 3N2 addition operations.
3.3
Adaptive Filtering using MATLAB
MATLAB is the acronym of Matrix Laboratory was originally designed to serve as
the interactive link to the numerical computation libraries LINPACK and EISPACK that
were used by engineers and scientists when they were dealing with sets of equations. The
MATLAB software was originally developed at the University of New Mexico and Stanford
University in the late 1970s. By 1984, a company was established named as Matwork by Jack
Little and Cleve Moler with the clear objective of commercializing MATLAB. Over a million
engineers and scientists use MATLAB today in well over 3000 universities worldwide and it
is considered a standard tool in education, business, and industry.
The basic element in MATLAB is the matrix and unlike other computer languages it
does not have to be dimensioned or declared. MATLAB’s main objective was to solve
mathematical problems in linear algebra, numerical analysis, and optimization but it quickly
evolved as the preferred tool for data analysis, statistics, signal processing, control systems,
economics, weather forecast, and many other applications. Over the years, MATLAB has
evolved creating an extended library of specialized built-in functions that are used to generate
among other things two-dimensional (2-D) and 3-D graphics and animation and offers
28](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-41-320.jpg)

![Major Software Characteristics:
i.
Matrix based numeric computation.
ii.
High level programming language.
iii.
Toolboxes provide application-specific functionality.
iv.
Multiple Platform Support.
v.
Open and Extensible System Architecture.
vi.
Interfaces to other language (C, FORTRAN etc).
For the simulation of the algorithms discussed in sec.3.2 MATLAB Version
7.4.0.287(R2007a) software is used. In the experimental setup, first of all high level
MATLAB programs [5],[20] are written for LMS , NLMS and RLS algorithms as per the
implementation steps described in sec.3.2.1.2, sec.3.2.2.2 and sec. 3.2.3.2 respectively [44] .
Then the simulation of above algorithms is done with a noisy tone signal generated through
MATLAB commands (refer sec. 6.1). The inputs to the programs are; the tone signal as
primary input s(n), random noise signal as reference input x(n), order of filter (N), step size
value (µ) ,number of iterations (refer Fig. 6.1) whereas the outputs are: the filtered output and
MSE which can be seen in the graphical results obtained after simulation gets over( refer
Fig.6.2).
The output results for the MATLAB simulation of LMS, NLMS and RLS algorithm
are presented and discussed later in the chapter-6.
30](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-43-320.jpg)
![Chapter-4
SIMULINK MODEL DESIGN FOR HARDWARE IMPLEMENTATION
4.1
Introduction to Simulink
Simulink is a software package for modeling, simulating and analyzing dynamic
systems [46]. It supports linear and nonlinear systems modeled in continuous time, sampled
time, or a hybrid of the two. Systems can also be multi rate, i.e. have different parts that are
sampled or updated at different rates. For modeling, simulink provides a graphical user
interface (GUI) for building models as block diagrams, using click-and-drag mouse
operations. With this interface, we can draw the models just as we would with pencil and
paper (or as most textbooks depict them). Simulink includes a comprehensive block library of
sinks, sources, linear and nonlinear components, and connectors. We can also customize and
create our own blocks.
Models are hierarchical, so we can build models using both top-down and bottom-up
approaches. We can view the system at a high level and then double-click blocks to go down
through the levels and thus visualize the model details. This approach provides insight into
how a model is organized and how its parts interact. After we define a model, we can
simulate it using a choice of integration methods either from the simulink menu or by
entering commands in the MATLAB command window.
In simulink, the menu is particularly convenient for interactive work. The command
line approach is very useful for running a batch of simulations (for example, if we want to
sweep a parameter across a range of values). Using scopes and other display blocks, we can
see the simulation results while the simulation is running. In addition, we can change many
parameters and see what happens. The simulation results can be put in the MATLAB
workspace for post processing and visualization.
The simulink model can be applied for modeling various time-varying systems that
includes control systems, signal processing systems, video processing systems, image
processing systems, communication and satellite systems, ship systems, automotive systems,
monetary systems, aircraft & spacecraft dynamics systems, and biological systems as
illustrated in Fig.4.1.
31](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-44-320.jpg)












![Fig.4.14. Changing the output data type
4.3.10 Switch Settings
The switch which is used in this model has three inputs viz. input 1, input 2 and input
3 numbered from top to bottom (refer Fig 4.2). The input 1 & input 3 are data inputs and
input 2 is the control input. When input 2 satisfies the selection criteria, input 1 is passed to
the output port otherwise input 3. The switch is configured as:
Double click on the “switch”
Set the criteria for passing first input to “u2>=Threshold”
Click “ok”
The simulink model for the hardware implementation of NLMS algorithm is
designed successfully and the designed model is reconfigured to meet the requirement of
TMS320C6713 DSP Processor environment. The reconfigured model shown in Fig.4.2 is
ready to connect with Code Composer Studio [50] and DSP Processor with the help of RTDX
link and Real-Time Workshop [47]. This is presented in chapter5.
44](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-57-320.jpg)
![Chapter-5
REAL-TIME IMPLEMENTATION ON DSP PROCESSOR
Digital signal processors are fast special-purpose microprocessors with a specialized
type of architecture and an instruction set appropriate for signal processing [45]. The
architecture of the digital signal processor is very well suited for numerically intensive
calculations. Digital signal processors are used for a wide range of applications which
includes communication, control, speech processing, image processing etc. These processors
have become the products of choice for a number of consumer applications, because they are
very cost-effective and can be reprogrammed easily for different applications.
DSP techniques have been very successful because of the development of low-cost
software and hardware support [48]. DSP processors are concerned primarily with real-time
signal processing. Real-time processing requires the processing to keep pace with some
external event, whereas non-real-time processing has no such timing constraint. The external
event is usually the analog input. Analog-based systems with discrete electronic components
such as resistors can be more sensitive to temperature changes whereas DSP-based systems
are less affected by environmental conditions.
In this chapter we will learn how we can realize or implement an adaptive filter on
hardware for real-time experiments. The model which was designed in previous chapter will
be linked to the DSP processor with help of Real Time Data Exchange (RTDX) utility
provided in simulink.
5.1
Introduction to Digital Signal Processor (TMS320C6713)
The TMS320C6713 is a low cost board designed to allow the user to evaluate the
capabilities of the C6713 DSP and develop C6713-based products [49]. It demonstrates how
the DSP can be interfaced with various kinds of memories, peripherals, Joint Text Action
Group (JTAG) and parallel peripheral interfaces.
The board is approximately 5 inches wide and 8 inches long as shown in Fig.5.2 and
is designed to sit on the desktop external to a host PC. It connects to the host PC through a
USB port. The processor board includes a C6713 floating-point digital signal processor and a
45](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-58-320.jpg)
![32-bit stereo codec TLV320AIC23 (AIC23) for input and output. The onboard codec AIC23
uses a sigma–delta technology that provides ADC and DAC. It connects to a 12-MHz system
clock. Variable sampling rates from 8 to 96 kHz can be set readily [51].
A daughter card expansion is also provided on the DSK board. Two 80-pin connectors
provide for external peripheral and external memory interfaces. The external memory
interface (EMIF) performs the task of interfacing with the other memory subsystems. Lightemitting diodes (LEDs) and liquid-crystal displays (LCDs) are used for spectrum display.
The DSK board includes 16MB (Megabytes) of synchronous dynamic random access
memory (SDRAM) and 256kB (Kilobytes) of flash memory.
Four connectors on the board provide inputs and outputs: MIC IN for microphone
input, LINE IN for line input, LINE OUT for line output, and HEADPHONE for a
headphone output (multiplexed with line output). The status of the four users DIP switches on
the DSK board can be read from a program and provides the user with a feedback control
interface (refer Fig.5.1 & Fig.5.2). The DSK operates at 225MHz.Also onboard are the
voltage regulators that provide 1.26 V for the C6713 core and 3.3V for its memory and
peripherals.
The major DSK hardware features are:
A C6713 DSP operating at 225 MHz.
An AIC23 stereo codec with Line In, Line Out, MIC, and headphone stereo jacks.
16 Mbytes of synchronous DRAM (SDRAM).
512 Kbytes of non-volatile Flash memory (256 Kbytes usable in default
configuration).
Four user accessible LEDs and DIP switches.
Software board configuration through registers implemented in complex logic device.
Configurable boot options.
Expansion connectors for daughter cards.
JTAG emulation through onboard JTAG emulator with USB host interface or external
Emulator.
Single voltage power supply (+5V).
46](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-59-320.jpg)

![5.1.1
Central Processing Unit Architecture
The CPU has Very Large Instruction Word (VLIW) architecture [53]. The CPU
always fetches eight 32-bit instructions at once and there is a 256-bit bus to the internal
program memory. Each group of eight instructions is called a fetch packet. The CPU has
eight functional units that can operate in parallel and are equally split into two halves, A and
B. All eight units do not have to be given instruction words if they are not ready. Therefore,
instructions are dispatched to the functional units as execution packets with a variable
number of 32-bit instruction words. The functional block diagram of Texas Instrument (TI)
processor architecture is shown below in Fig.5.3.
32
EMIF
McASP1
McASP0
McBSP0
Pin Multiplexing
I2C1
I2C0
Timer 1
Timer 0
Enhanced DMA Controller
(16 Channel)
McBSP1
L2 Cache
Memory
4 Banks
64K Bytes
Total
(Up to 4‐
way)
L2
Memory
192K
Bytes
C67x CPU
Instruction Fetch
Instruction Dispatch
Instruction Decode
Data Path A Data Path B
A Register File B Register
.L1 .S1 .M1 .D1
.D2 .M2 .S2 .L2
HPI
Control
Register
Control
Test
In‐Circuit
Emulation
Interrupt
Control
L1D Cache
2‐Way
Set Associative
4K Bytes
Clock Generator
Oscillator and PLL
×4 through ×25
Multiplier
/1 through /32 Divider
GPIO
16
LIP Cache
Direct Mapped
4 Bytes Total
Power –
Down Logic
Fig.5.3. Functional block diagram of TMS320C6713 CPU
The eight functional units include:
Four ALU that can perform fixed and floating-point operations (.L1, .L2, .S1, .S2).
Two ALU’s that perform only fixed-point operations (.D1, .D2).
48](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-61-320.jpg)



![The microphone input is a high-impedance, low-capacitance input compatible with a
wide range of microphones.
The DAC for the line outputs has a full-scale output voltage range of 1.0 V RMS.
The stereo headphone outputs are designed to drive 16 or 32-ohm headphones.
The AIC23 has an analog bypass mode that directly connects the analog line inputs to
the analog line outputs.
The AIC23 has a side tone insertion mode where the microphone input is routed to the
line and headphone outputs.
AIC23 Codec
FSX1
CLKX1
TX1
CONTROL
SPI Format
CS
SCLK
SD IN
Digital
Control Registers
McBSP0
0
1
2
3
4
5
6
7
8
9
15
LEFT IN VOL
RIGHT IN VOL
LEFT HP VOL
RIGHT HP VOL
ANAPATH
DIGPATH
POWER DOWN
DIGIF
SAMPLE RATE
DIGACT
RESET
DATA
McBSP1
DR2
FX2
CLKR
CLKX
FSR2
DX2
D OUT
LRC OUT
B CLK
LRC IN
D IN
MIC IN
LINE IN
Analog
LINE OUT
MIC IN
ADC
LINE IN
DAC
LINE OUT
HP OUT
HP OUT
Fig.5.7. AIC23 codec interface
5.1.5 DSP/BIOS & RTDX
The DSP/BIOS facilities utilize the Real-Time Data Exchange (RTDX) link to obtain
and monitor target data in real-time [47]. I utilized the RTDX link to create my own
customized interfaces to the DSP target by using the RTDX API Library. The RTDX
transfers data between a host computer and target devices without interfering with the target
application. This bi-directional communication path provides data collection by the host as
well as host interaction while running target application. RTDX also enables host systems to
provide data stimulation to the target application and algorithms.
52](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-65-320.jpg)

![5.2 Code Composer Studio as Integrated Development Environment
Code Composer Studio is the DSP industry's first fully integrated development
environment (IDE) [50] with DSP-specific functionality. With a familiar environment like
MS-based C++TM; Code Composer lets you edit, build, debug, profile and manage projects
from a single unified environment. Other unique features include graphical signal analysis,
injection/extraction of data signals via file I/O, multi-processor debugging, automated testing
and customization via a C-interpretive scripting language and much more.
Fig.5.9. Code compose studio platform
Real-time analysis can be performed using real-time data exchange (RTDX). RTDX allows
for data exchange between the host PC and the target DSK, as well as analysis in real time without
stopping the target. Key statistics and performance can be monitored in real time. Through the joint
team action group (JTAG), communication with on-chip emulation support occurs to control and
monitor program execution. The C6713 DSK board includes a JTAG interface through the USB port.
Fig.5.10. Embedded software development
54](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-67-320.jpg)
![Source
Efficiency
Effort
Compiler
Optimizer
80‐100%
Low
Linear
ASM
Assembly
Optimizer
95‐100%
Med
ASM
Hand
Optimizer
100%
High
C
C++
Fig.5.11. Typical 67xx efficiency vs. efforts level for different codes
The Code composer studio supports three file formats (.c/c++, .sa, .asm) for writing
codes. Fig.5.11 shows the efficiency vs. efforts level for three kinds of source codes. If we
write the code in linear assembly then ASM optimizer is required to convert linear assembly
file (.sa) to assembly file (.asm). Similarly if the code is written in C, the C compiler is
required to produce an assembly source file with extension .asm. The assembler assembles
.asm source file to produce a machine language object file with extension .obj. The linker
combines object files and object libraries as input to produce an executable file with
extension .out. This executable file represents a linked common object file format (COFF),
popular in Unix-based systems and adopted by several digital signal processor developers
[52]. This executable file can be loaded and run directly on the C6713 processor. Fig.5.12
and Fig.5.13 illustrate the process of target file generation.
.sa
ASM
Optimizer
Text
Editor
Link.cm
Assembler
.asm
Linker
.obj
.c/.cpp
.map
Compiler
Fig.5.12. Code generation
55
.out](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-68-320.jpg)



![completed the output can be taken at HP OUT or LINE OUT port with the help of headphone
or CRO/DSO (refer Fig.5.17).
Fig.5.17. Experimental setup using Texas Instrument processor
Fig.5.18. Real-time experimental setup using DSP processor
The real time implementation can be done in the following manner: First of all, the
simulink model is developed (refer section 4.2) for NLMS algorithm and then connected to
the CCS by RTDX link to create a project in the CCS as shown in Fig.5.19 [47].
59](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-72-320.jpg)












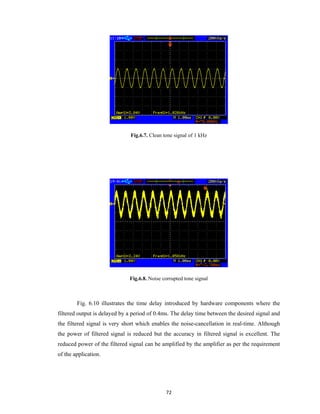















![REFERENCES
REFERENCE FROM PAPERS & JOURNALS:
[1]
Bernard Widrow, John R. Glover, John M. Mccool, John Kaunitz, Charles S. Williams,
Robert H. Hean, James R. Zeidler, Eugene Dong, Jr. and Robert C. Goodlin,
“Adaptive Noise Cancelling: Principles and Applications”, Proceedings of the IEEE,
vol.-63 , no.-12 , pp. 1692-1716, December 1975.
[2]
Abutaleb, A.S, “An adaptive filter for noise cancelling”, IEEE Transactions on Circuits
and Systems, vol.-35, no.-10, pp. 1201-1209, October 1988.
[3]
Abhishek Tandon, M. Omair Ahmad, “An efficient, low-complexity, Normalized LMS
algorithm for echo cancellation” The 2nd Annual IEEE Northeast Workshop on Circuits
and Systems, pp. 161-164, June 2004.
[4]
DONG Hang and SUN Hong, “Multirate Algorithm for Updating the Coefficients of
Adaptive Filter”, First International Conference on Intelligent Networks and Intelligent
Systems, pp. 581-584, November 2008.
[5]
Ying He, Hong He, Yi Wu and Hongyan Pan, “The Applications and Simulation of
Adaptive Filter in Noise Canceling”, International Conference on Computer Science
and Software Engineering, vol.-4, pp. 1-4, December 2008.
[6]
Edgar Andrei Vega Ochoa and Manuel Edgardo Guzman Renteria, “A real time
acoustic echo canceller implemented on the Motorola DSP56307”, IEEE International
Symposium on Industrial Electronics, vol.-2, pp. 625-630, December 2000.
[7]
Michail D. Galanis and Athanassios Papazacharias, “A DSP Course for Real-Time
Systems Design and Implementation based on TMS320C6211 DSK”, 14th
International Conference on Digital Signal Processing, vol.-2, pp. 853-856,
December 2002.
[8]
Boo-Shik Ryu, Jae-Kyun Lee, Joonwan Kim, Chae-Wook Lee, “The Performance of an
adaptive noise canceller with DSP processor”, 40th IEEE Southeastern Symposium on
System Theory, pp. 42-45, March 2008.
[9]
Gerardo Avalos, Daniel Espinobarro, Jose Velazquez, Juan C. Sanchez, “Adaptive
Noise Canceller using LMS algorithm with codified error in a DSP”, 52nd IEEE
International Midwest Symposium on Circuits and Systems, pp. 657-662, August 2009.
[10] J.C. Duran Villalobos, C.A., Tavares Reyes, J.A., Sanchez Garcia, “Implementation and
Analysis of the NLMS Algorithm on TMS320C6713 DSP”, 52nd IEEE International
Midwest Symposium on Circuits and Systems, pp. 1091-1096, August 2009.
88](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-101-320.jpg)
![[11] Gaurav Saxena, Subramaniam Ganesan, and Manohar Das, “Real time implementation
of adaptive noise cancellation”, IEEE International conference on electro/information
technology, pp. 431-436, May 2008.
[12] Hasnain, S.K. Daruwalla, A.D. Saleem, “A unified approach in audio signal
processing using the TMS320C6713 and simulink blocksets”, 2nd International
Conference on Computer, Control and Communication, pp. 1-5, February 2009.
[13] Yaghoub Mollaei, “Hardware Implementation of Adaptive filters”, Proceedings of
IEEE Student Conference on Research and Development, UPM Serdang, Malaysia,
pp. 45-48, November 2009.
[14] Slock, D.T.M., “On the convergence behavior of the LMS and the normalized LMS
algorithms”, IEEE Transactions on Signal Processing, vol.- 41, no.- 9, pp. 2811-2825,
September 1993.
[15] Sanaullah Khan, M.Arif and T.Majeed, “Comparison of LMS, RLS and Notch Based
Adaptive Algorithms for Noise Cancellation of a typical Industrial Workroom”, 8th
International Multi-topic Conference, pp. 169-173, December 2004.
[16] Yuu-Seng Lau, Zahir M. Hussian and Richard Harris, “Performance of Adaptive
Filtering Algorithms: A Comparative Study”, Australian Telecommunications,
Networks and Applications Conference (ATNAC), Melbourne, 2003.
[17] Thomas Schertler, “Selective Block Update of NLMS type Algorithms”, IEEE
International Conference on Acoustics, Speech and Signal Processing, vol.-3, pp. 17171720, May1998.
[18] Andy W. H. Khong, “Stereophonic Acoustic Echo Cancellation Employing SelectiveTap Adaptive Algorithms”, IEEE Transactions on Audio, Speech, and Language
Processing, vol.- 14, no.- 3, pp. 785-796, May 2006.
[19] Amit S. Chhetri, Jack W. Stokes, Dinei A. Florˆencio, “Acoustic Echo Cancelation for
High Noise Environments”, IEEE International Conference on Multimedia and Expo,
pp. 905-908, July 2006.
[20] Amrita Rai and Amit Kumar Kohli, “Analysis and Simulation of Adaptive Filter with
LMS Algorithm”, International Journal of Electronics Engineering, vol.-2, no.-1, pp.
121-123, January 2010.
[21] J. Benesty , F. Amand , A. Gilloire and Y. Grenier , “Adaptive Filtering Algorithms for
Stereophonic Acoustic Echo Cancellation”, International Conference on Acoustics,
Speech, and Signal Processing, vol.-5, pp. 3099-3102, May 1995.
89](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-102-320.jpg)
![[22] Nuha A. S. Alwan, “On the Effect of Tap Length on LMS Adaptive Echo Canceller
Performance”, International conference on Computer engineering and Systems,
pp. 197-201, November 2006.
[23] Sen. M. Kuo and Huan Zhao, “A Real-Time Acoustic Echo Cancellation System”,
IEEE International Conference on Systems Engineering, pp. 168-171, August 1990.
[24] Andre' H.C. Carezia, Phillip M.S. Burt, Max Gerken, Maria D. Mirandat, Magno T.M.
da Silva, “A Stable and Efficient DSP Implementation of A LSL Algorithm for
Acoustic Echo Cancelling”, IEEE International Conference on Acoustics, Speech, and
Signal Processing, vol.-2, pp. 921-924, May 2001.
[25] G. Di Natale, A. Serra, C. Turcotti, “A Board Implementation for Fast APA Acoustic
Echo Canceller Using ADSP-21065L DSP”, IEEE International Conference on
Automation, Quality Testing and Robotics, vol.2-, pp. 339-344, May 2006.
[26] Ali A. Milani, Issa M.S Panahi, Richard Briggs, “Distortion Analysis of Subband
Adaptive Filtering Methods for fMRI Active Noise Control Systems”, IEEE
Proceedings of the 29th Annual International Conference of the IEEE EMBS Cité
Internationale, Lyon, France, pp. 3296-3299, August 2007.
[27] Dornean, M. Topa, B.S. Kirei, G. Oltean, “HDL Implementation of the Variable Step
Size N-LMS Adaptive Algorithm”, IEEE International conference on Automation,
Quality and testing,Robotics, vol.-3, pp. 243-246, May 2008.
[28] Satoshi Yamazaki, David K.Asano, “A Serial Unequal Error Protection Code System
using Trellis Coded Modulation and an Adaptive Equalizer for Fading Channels”, 14th
Asia-Pacific IEEE Conference on Communications, pp. 1-5, October 2008.
[29] Gye-Tae Gil, “Normalized LMS Adaptive Cancellation of Self-Image in DirectConversion Receivers”, IEEE Transactions on vehicular technology, vol.- 58, no.- 2,
pp. 535-545, February 2009
[30] Sorin Zoican, “A Nonlinear Acoustic Echo Cancellation Scheme Implementation Using
the Blackfin Microcomputer”, 9th International IEEE Conference on
Telecommunication in Modern Satellite, Cable, and Broadcasting Services, pp. 237240, October 2009.
[31] Cristian Anghel, Constantin Paleologu, Jacob Benesty, and Silviu Ciochină, “FPGA
Implementation of an Acoustic Echo Canceller Using a VSS-NLMS Algorithm”,
International Symposium on Signals, Circuits and Systems, pp. 1-4, July 2009.
[32] Sangil Park, “Real-Time Implementation of New Adaptive Detection Structures using
the DSP56001”, IEEE International Conference on Systems Engineering, pp. 281-284,
August 1989.
90](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-103-320.jpg)
![[33] Paulo A. C. Lopes, Gonc¸alo Tavares and Jos´e B. Gerald, “A New type of Normalized
LMS Algorithm based on The Kalman Filter”, IEEE International Conference on
Acoustics, Speech and Signal Processing, pp. 1345-1348, April 2007.
[34] John Hakon , “A Circulantly Preconditioned NLMS-type Adaptive Filter”, 17th
International Conference Radioelektronika, pp. 1-5, April 2007.
[35] Jinhong Wu and Milos Doroslovacki, “A Mean Convergence Analysis for Partial
Update NLMS Algorithms”, 41st Annual IEEE Conference on Information Sciences
and Systems, pp. 31-34, March 2007.
[36] John H˚akon Husøy, Øyvind Lunde Rørtveit, “An NLMS-type Adaptive Filter Using
Multiple Fixed Preconditioning Matrices”, International Conference on Signals and
Electronic Systems, Kraków, September, 2008.
[37] Ch. Renumadhavi, Dr. S.Madhava Kumar, Dr. A. G. Ananth, Nirupama Srinivasan, “A
New Approach for Evaluating SNR of ECG Signals and Its Implementation”,
Proceedings of the 6th WSEAS International Conference on Simulation, Modelling and
Optimization, Lisbon, Portugal, September 2006.
[38] Riitta Niemist¨o and Tuomo M¨akel, “On Performance of Linear Adaptive Filtering
Algorithms in Acoustic Echo Control in Presence of Distorting Loudspeakers”,
International Workshop on Acoustic echo and Noise Control, Kyoto, Japan,
September 2003.
[39] Cristina Gabriela SĂRĂCIN, Marin SĂRĂCIN, Mihai DASCĂLU, Ana-Maria
LEPAR, “Echo Cancellation Using The LMS Algorithm”, U.P.B. Sci. Bull., Series C,
vol.- 71, no.- 4, April 2009.
[40] Ajay Kr. Singh, G. Singh, D. S. Chauhan, “Implementation of Real Time Programs on
the TMSC6713DSK Processor”, International Journal of Signal and Image Processing,
vol.- 1, no.-3, pp. 160-168, March 2010.
[41] Ali O. Abid Noor, Salina Abdul Samad and Aini Hussain, “Improved, Low Complexity
Noise Cancellation Technique for Speech Signals”, World Applied Sciences Journal,
vol.- 6, no.-2, pp. 272-278, February 2009.
REFERENCE FROM BOOKS & MANUALS:
[42] Simon Haykin, “Adaptive Filter Theory”, ISBN 978-0130901262, Prentice Hall,
4th edition, 2001.
[43] Paulo S.R. Diniz, “Adaptive Filtering: Algorithms and Practical Implementations”,
ISBN 978-0-387-31274-3, Kluwer Academic Publisher © 2008 Springer
Science+Business Media, LLC.
91](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-104-320.jpg)
![[44] Alexander D. Poularikas “Adaptive filtering Primer with MATLAB”, ISBN 978-08493-7043-4, CRC Press, 2006.
[45] Donald Reay, “Digital Signal Processing and Applications with the TMS320C6713 and
TMS320C6416 DSK”, ISBN 978-0-470-13866-3, John Wiley & Sons, Inc., Edition- 2nd
2008.
[46] MathWorks Documentation, “Simulink 6.6 User’s Guide”, March 2007.
[47] MathWorks Documentation, “Real-Time Workshop 6.6 User’s Guide” March 2007.
[48] MathWorks User’s Guide, “Target Support Package for Use with TI’s C6000™ 4”.
[49] Texas Instruments Tutorial, “TMS320C6713 Floating-Point Digital Signal Processor”,
(December 2001 – Revised November 2005), SPRS186L
[50] Texas Instruments Tutorial, “Code Composer Studio Development Tools v3.3 Getting
Started Guide”, (Oct 2006), SPRU509H
[51] Texas Instruments Tutorial, “TMS320C6000 Instruction Set Simulator Technical
Reference Manual”, (April 2007), SPRS600I
[52] Texas Instruments Tutorial, “How to Begin Development Today With the
TMS320C6713 Floating-Point DSP”, (October 2002), SPRA809A
[53] Texas Instruments Tutorial, “TMS320C6713 Hardware Designers Resource Guide”,
(July 2004), SPRAA33
92](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-105-320.jpg)
![APPENDIX-I
LIST OF PUBLICATIONS
International/ National Journals (Published/Accepted)
[1] Raj kumar Thenua and S.K. Agarwal, “Simulation and Performance Analysis of
Adaptive Filter in Noise Cancellation”, International Journal of Engineering Science
and Technology (IJEST), ISSN: 0975-5462, Vol. 2(9), 2010, Page no. 4374-4379.
(Published)
International/ National Conferences (Published/Accepted)
[2] Raj kumar Thenua and S.K. Agarwal, “Hardware Implementation of Adaptive
algorithms for Noise Cancellation”, IEEE International Conference on Network
Communication and Computer (ICNCC 2011), 21st -23rd Mar 2011, organized by
International Association of Computer Science and Information Technology (IACSIT)
and Singapore Institute of Electronics (SIE) at New Delhi, India. (Published)
[3] Raj kumar Thenua, S.K. Agarwal and Mohd. Ayub khan, “Performance analyses of
Adaptive Noise Canceller for an ECG signal” International Conference on Recent
Trends in Engineering, Technology and Management on 26th -27th Feb 2011 at BIET,
Jhansi, India. (Published)
[4] Raj kumar Thenua and S.K. Agarwal, “Hardware Implementation of NLMS
Algorithm for Adaptive Noise Cancellation”, National Conference on Electronics and
Communication (NCEC-2010) on 22nd -24th December 2010 at MITS, Gwalior.
(Published)
[5] Raj kumar Thenua and S.K. Agarwal, “Real-time Noise Cancellation using Digital
Signal Processor”, National conference on Electronics, Computers and
Communications (NCECC-2010) on 06th -07th March 2010 at MITS, Gwalior.
(Published)
93](https://image.slidesharecdn.com/rajkumarthenuathesisfinal-131203040808-phpapp01/85/M-Tech-Thesis-on-Simulation-and-Hardware-Implementation-of-NLMS-algorithm-on-TMS320C6713-Digital-Signal-Processor-106-320.jpg)
