Optimal binary search tree dynamic programming
1 like3,552 views
The document discusses optimal binary search trees (OBST) and describes the process of creating one. It begins by introducing OBST and noting that the method can minimize average number of comparisons in a successful search. It then shows the step-by-step process of calculating the costs for different partitions to arrive at the optimal binary search tree for a given sample dataset with keys and frequencies. The process involves calculating Catalan numbers for each partition and choosing the minimum cost at each step as the optimal is determined.
![OBST CREATION
No. of Nodes = 0
(j-i)=0
(0-0) = 0 = C[0,0]
(1-1) = 0 = C[1,1]
(2-2) = 0 = C[2,2]
(3-3) = 0 = C[3,3]
(4-4) = 0 = C[4,4]
Item 1 2 3 4
Key 10 20 30 40
Freq 4 2 6 3
i j 0 1 2 3 4
0 0
1 0
2 0
3 0
4 0
6](https://image.slidesharecdn.com/optimalbinarysearchtree-dynamicprogramming-200407124300/85/Optimal-binary-search-tree-dynamic-programming-6-320.jpg)
![OBST CREATION
No. of Nodes = 1
(j-i)=1
(1-0) = 1 = C[0,1]
(2-1) = 1 = C[1,2]
(3-2) = 1 = C[2,3]
(4-3) = 1 = C[3,4]
Item 1 2 3 4
Key 10 20 30 40
Freq 4 2 6 3
i j 0 1 2 3 4
0 0
1 0
2 0
3 0
4 0
Dr. P. Subathra, KAMARAJ College of Engg &
Tech (AUTONOMOUS), Madurai,
Tamil Nadu, India
7](https://image.slidesharecdn.com/optimalbinarysearchtree-dynamicprogramming-200407124300/85/Optimal-binary-search-tree-dynamic-programming-7-320.jpg)
![OBST CREATION
No. of Nodes = 1
(j-i)=1
(1-0) = 1 = C[0,1] = 41
(2-1) = 1 = C[1,2]
(3-2) = 1 = C[2,3]
(4-3) = 1 = C[3,4]
Item 1 2 3 4
Key 10 20 30 40
Freq 4 2 6 3
i j 0 1 2 3 4
0 0 41
1 0
2 0
3 0
4 0
Dr. P. Subathra, KAMARAJ College of Engg &
Tech (AUTONOMOUS), Madurai,
Tamil Nadu, India
8](https://image.slidesharecdn.com/optimalbinarysearchtree-dynamicprogramming-200407124300/85/Optimal-binary-search-tree-dynamic-programming-8-320.jpg)
![OBST CREATION
No. of Nodes = 1
(j-i)=1
(1-0) = 1 = C[0,1] = 41
(2-1) = 1 = C[1,2] = 22
(3-2) = 1 = C[2,3]
(4-3) = 1 = C[3,4]
Item 1 2 3 4
Key 10 20 30 40
Freq 4 2 6 3
i j 0 1 2 3 4
0 0 41
1 0 22
2 0
3 0
4 0
Dr. P. Subathra, KAMARAJ College of Engg &
Tech (AUTONOMOUS), Madurai,
Tamil Nadu, India
9](https://image.slidesharecdn.com/optimalbinarysearchtree-dynamicprogramming-200407124300/85/Optimal-binary-search-tree-dynamic-programming-9-320.jpg)
![OBST CREATION
No. of Nodes = 1
(j-i)=1
(1-0) = 1 = C[0,1] = 41
(2-1) = 1 = C[1,2] = 22
(3-2) = 1 = C[2,3] = 63
(4-3) = 1 = C[3,4]
Item 1 2 3 4
Key 10 20 30 40
Freq 4 2 6 3
i j 0 1 2 3 4
0 0 41
1 0 22
2 0 63
3 0
4 0
Dr. P. Subathra, KAMARAJ College of Engg &
Tech (AUTONOMOUS), Madurai,
Tamil Nadu, India
10](https://image.slidesharecdn.com/optimalbinarysearchtree-dynamicprogramming-200407124300/85/Optimal-binary-search-tree-dynamic-programming-10-320.jpg)
![OBST CREATION
No. of Nodes = 1
(j-i)=1
(1-0) = 1 = C[0,1] = 41
(2-1) = 1 = C[1,2] = 22
(3-2) = 1 = C[2,3] = 63
(4-3) = 1 = C[3,4] = 34
Item 1 2 3 4
Key 10 20 30 40
Freq 4 2 6 3
i j 0 1 2 3 4
0 0 41
1 0 22
2 0 63
3 0 34
4 0
Dr. P. Subathra, KAMARAJ College of Engg &
Tech (AUTONOMOUS), Madurai,
Tamil Nadu, India
11](https://image.slidesharecdn.com/optimalbinarysearchtree-dynamicprogramming-200407124300/85/Optimal-binary-search-tree-dynamic-programming-11-320.jpg)
![OBST CREATION
No. of Nodes = 2
(j-i)=2
(2-0) = 2 = C[0,2]
(3-1) = 2 = C[1,3]
(4-2) = 2 = C[2,4]
Item 1 2 3 4
Key 10 20 30 40
Freq 4 2 6 3
i j 0 1 2 3 4
0 0 41
1 0 22
2 0 63
3 0 34
4 0
Dr. P. Subathra, KAMARAJ College of Engg &
Tech (AUTONOMOUS), Madurai,
Tamil Nadu, India
12](https://image.slidesharecdn.com/optimalbinarysearchtree-dynamicprogramming-200407124300/85/Optimal-binary-search-tree-dynamic-programming-12-320.jpg)
![OBST CREATION
No. of Nodes = 2 : (1&2)
C[0,2] : i = 0; j =2; k = 1, 2;
k =1
C[0, 1-1] + C[1, 2]
= min k=2 + (W1+W2)
C[0, 2-1] + C[2, 2]
= min k= 1 (0+2)
k= 2 (0+6)
= 2 + 6 = 81
Item 1 2 3 4
Key 10 20 30 40
Freq (W) 4 2 6 3
i j 0 1 2 3 4
0 0 41 81
1 0 22
2 0 63
3 0 34
4 0
+ (4+2)
13](https://image.slidesharecdn.com/optimalbinarysearchtree-dynamicprogramming-200407124300/85/Optimal-binary-search-tree-dynamic-programming-13-320.jpg)
![OBST CREATION
No. of Nodes = 2 : (2&3)
C[1,3] : i = 1; j =3; k = 2, 3;
k =2
C[1, 2-1] + C[2, 3]
= min k=3 + (W2+W3)
C[1, 3-1] + C[3, 3]
= min k= 2 (0+6)
k= 3 (2+0)
= 2 + 8 = 103
Item 1 2 3 4
Key 10 20 30 40
Freq
(W)
4 2 6 3
i j 0 1 2 3 4
0 0 41 81
1 0 22 103
2 0 63
3 0 34
4 0
+ (2+6)
14](https://image.slidesharecdn.com/optimalbinarysearchtree-dynamicprogramming-200407124300/85/Optimal-binary-search-tree-dynamic-programming-14-320.jpg)
![OBST CREATION
No. of Nodes = 2 : (3&4)
C[2,4] : i = 2; j =4; k = 3, 4;
k =3
C[2, 3-1] + C[3, 4]
= min k=4 + (W2+W3)
C[2, 4-1] + C[4, 4]
= min k= 3 (0+3)
k= 4 (6+0)
= 3 + 9 = 123
Item 1 2 3 4
Key 10 20 30 40
Freq (W) 4 2 6 3
i j 0 1 2 3 4
0 0 41 81
1 0 22 103
2 0 63 123
3 0 34
4 0
+ (6+3)
15](https://image.slidesharecdn.com/optimalbinarysearchtree-dynamicprogramming-200407124300/85/Optimal-binary-search-tree-dynamic-programming-15-320.jpg)
![OBST CREATION
No. of Nodes = 3 :
(j-i) = 3
(3-0) = 3 = C[0,3]
(4-1) = 3 = C[1,4]
Item 1 2 3 4
Key 10 20 30 40
Freq (W) 4 2 6 3
i j 0 1 2 3 4
0 0 41 81
1 0 22 103
2 0 63 123
3 0 34
4 0
Dr. P. Subathra, KAMARAJ College of Engg &
Tech (AUTONOMOUS), Madurai,
Tamil Nadu, India
16](https://image.slidesharecdn.com/optimalbinarysearchtree-dynamicprogramming-200407124300/85/Optimal-binary-search-tree-dynamic-programming-16-320.jpg)
![OBST CREATION
No. of Nodes = 3 : (1,2&3)
C[0,3] : i = 0; j =3; k = 1,2,3;
k =1
C[0, 1-1] + C[1, 3]
= min k=2
C[0, 2-1] + C[2, 3]
k=3 + (W1+W2+W3)
C[0, 3-1] + C[3, 3]
= min k= 1 (0+10)
k= 2 (4+6)
k= 3 (8+0)
= 8 + 12 = 203
Item 1 2 3 4
Key 10 20 30 40
Freq (W) 4 2 6 3
i j 0 1 2 3 4
0 0 41 81 203
1 0 22 103
2 0 63 123
3 0 34
4 0
+ (4+2+6)
17](https://image.slidesharecdn.com/optimalbinarysearchtree-dynamicprogramming-200407124300/85/Optimal-binary-search-tree-dynamic-programming-17-320.jpg)
![OBST CREATION
No. of Nodes = 3 : (2,3 & 4)
C[1,4] : i = 1; j =4; k = 2,3,4;
k =2
C[1, 2-1] + C[2, 4]
= min k=3
C[1, 3-1] + C[3, 4]
k=4 + (W2+W3+W4)
C[1, 4-1] + C[4, 4]
= min k= 2 (0+12)
k= 3 (2+3)
k= 4 (10+0)
= 5 + 11 = 163
Item 1 2 3 4
Key 10 20 30 40
Freq (W) 4 2 6 3
i j 0 1 2 3 4
0 0 41 81 203
1 0 22 103 163
2 0 63 123
3 0 34
4 0
+ (2+6+3)
18](https://image.slidesharecdn.com/optimalbinarysearchtree-dynamicprogramming-200407124300/85/Optimal-binary-search-tree-dynamic-programming-18-320.jpg)
![OBST CREATION
No. of Nodes = 4 :
(j-i) = 4
(4-0) = 4 = C[0,4]
Item 1 2 3 4
Key 10 20 30 40
Freq (W) 4 2 6 3
i j 0 1 2 3 4
0 0 41 81 203
1 0 22 103 163
2 0 63 123
3 0 34
4 0
Dr. P. Subathra, KAMARAJ College of Engg &
Tech (AUTONOMOUS), Madurai,
Tamil Nadu, India
19](https://image.slidesharecdn.com/optimalbinarysearchtree-dynamicprogramming-200407124300/85/Optimal-binary-search-tree-dynamic-programming-19-320.jpg)
![OBST CREATION
No. of Nodes = 4 : (1,2,3 & 4)
C[0,4] : i = 0; j =4; k = 1,2,3,4;
k=1
C[0, 1-1] + C[1, 4]
k =2
C[0, 2-1] + C[2, 4]
= min k=3
C[0, 3-1] + C[3, 4]
k=4 + (W1+W2+W3+W4)
C[0, 4-1] + C[4, 4]
= min k=1 (0+16)
k= 2 (4+12)
k= 3 (8+3)
k= 4 (20+0)
= 11 + 15 = 263
Item 1 2 3 4
Key 10 20 30 40
Freq (W) 4 2 6 3
i j 0 1 2 3 4
0 0 41 81 203 263
1 0 22 103 163
2 0 63 123
3 0 34
4 0
+ (4+2+6+3)
20](https://image.slidesharecdn.com/optimalbinarysearchtree-dynamicprogramming-200407124300/85/Optimal-binary-search-tree-dynamic-programming-20-320.jpg)
Optimal binary search tree dynamic programming
- 1. Optimal Binary Search Tree Dr. P. Subathra Prof/ IT KAMARAJ College of Engg. & Tech (AUTONOMOUS) Madurai Tamil Nadu India
- 2. • If probabilities of searching for elements of a set are known—e.g., from accumulated data about past searches—it is natural to pose a question about an optimal binary search tree for which the average number of comparisons in a search is the smallest possible. • we limit our discussion to minimizing the average number of comparisons in a successful search. • The method can be extended to include unsuccessful searches as well. Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 2
- 3. • The total number of binary search trees with n keys is equal to the nth Catalan number Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 3
- 4. Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 4
- 5. OBST CREATION (j-i)=0 Item 1 2 3 4 Key 10 20 30 40 Freq 4 2 6 3 i j 0 1 2 3 4 0 1 2 3 4 Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 5
- 6. OBST CREATION No. of Nodes = 0 (j-i)=0 (0-0) = 0 = C[0,0] (1-1) = 0 = C[1,1] (2-2) = 0 = C[2,2] (3-3) = 0 = C[3,3] (4-4) = 0 = C[4,4] Item 1 2 3 4 Key 10 20 30 40 Freq 4 2 6 3 i j 0 1 2 3 4 0 0 1 0 2 0 3 0 4 0 6
- 7. OBST CREATION No. of Nodes = 1 (j-i)=1 (1-0) = 1 = C[0,1] (2-1) = 1 = C[1,2] (3-2) = 1 = C[2,3] (4-3) = 1 = C[3,4] Item 1 2 3 4 Key 10 20 30 40 Freq 4 2 6 3 i j 0 1 2 3 4 0 0 1 0 2 0 3 0 4 0 Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 7
- 8. OBST CREATION No. of Nodes = 1 (j-i)=1 (1-0) = 1 = C[0,1] = 41 (2-1) = 1 = C[1,2] (3-2) = 1 = C[2,3] (4-3) = 1 = C[3,4] Item 1 2 3 4 Key 10 20 30 40 Freq 4 2 6 3 i j 0 1 2 3 4 0 0 41 1 0 2 0 3 0 4 0 Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 8
- 9. OBST CREATION No. of Nodes = 1 (j-i)=1 (1-0) = 1 = C[0,1] = 41 (2-1) = 1 = C[1,2] = 22 (3-2) = 1 = C[2,3] (4-3) = 1 = C[3,4] Item 1 2 3 4 Key 10 20 30 40 Freq 4 2 6 3 i j 0 1 2 3 4 0 0 41 1 0 22 2 0 3 0 4 0 Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 9
- 10. OBST CREATION No. of Nodes = 1 (j-i)=1 (1-0) = 1 = C[0,1] = 41 (2-1) = 1 = C[1,2] = 22 (3-2) = 1 = C[2,3] = 63 (4-3) = 1 = C[3,4] Item 1 2 3 4 Key 10 20 30 40 Freq 4 2 6 3 i j 0 1 2 3 4 0 0 41 1 0 22 2 0 63 3 0 4 0 Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 10
- 11. OBST CREATION No. of Nodes = 1 (j-i)=1 (1-0) = 1 = C[0,1] = 41 (2-1) = 1 = C[1,2] = 22 (3-2) = 1 = C[2,3] = 63 (4-3) = 1 = C[3,4] = 34 Item 1 2 3 4 Key 10 20 30 40 Freq 4 2 6 3 i j 0 1 2 3 4 0 0 41 1 0 22 2 0 63 3 0 34 4 0 Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 11
- 12. OBST CREATION No. of Nodes = 2 (j-i)=2 (2-0) = 2 = C[0,2] (3-1) = 2 = C[1,3] (4-2) = 2 = C[2,4] Item 1 2 3 4 Key 10 20 30 40 Freq 4 2 6 3 i j 0 1 2 3 4 0 0 41 1 0 22 2 0 63 3 0 34 4 0 Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 12
- 13. OBST CREATION No. of Nodes = 2 : (1&2) C[0,2] : i = 0; j =2; k = 1, 2; k =1 C[0, 1-1] + C[1, 2] = min k=2 + (W1+W2) C[0, 2-1] + C[2, 2] = min k= 1 (0+2) k= 2 (0+6) = 2 + 6 = 81 Item 1 2 3 4 Key 10 20 30 40 Freq (W) 4 2 6 3 i j 0 1 2 3 4 0 0 41 81 1 0 22 2 0 63 3 0 34 4 0 + (4+2) 13
- 14. OBST CREATION No. of Nodes = 2 : (2&3) C[1,3] : i = 1; j =3; k = 2, 3; k =2 C[1, 2-1] + C[2, 3] = min k=3 + (W2+W3) C[1, 3-1] + C[3, 3] = min k= 2 (0+6) k= 3 (2+0) = 2 + 8 = 103 Item 1 2 3 4 Key 10 20 30 40 Freq (W) 4 2 6 3 i j 0 1 2 3 4 0 0 41 81 1 0 22 103 2 0 63 3 0 34 4 0 + (2+6) 14
- 15. OBST CREATION No. of Nodes = 2 : (3&4) C[2,4] : i = 2; j =4; k = 3, 4; k =3 C[2, 3-1] + C[3, 4] = min k=4 + (W2+W3) C[2, 4-1] + C[4, 4] = min k= 3 (0+3) k= 4 (6+0) = 3 + 9 = 123 Item 1 2 3 4 Key 10 20 30 40 Freq (W) 4 2 6 3 i j 0 1 2 3 4 0 0 41 81 1 0 22 103 2 0 63 123 3 0 34 4 0 + (6+3) 15
- 16. OBST CREATION No. of Nodes = 3 : (j-i) = 3 (3-0) = 3 = C[0,3] (4-1) = 3 = C[1,4] Item 1 2 3 4 Key 10 20 30 40 Freq (W) 4 2 6 3 i j 0 1 2 3 4 0 0 41 81 1 0 22 103 2 0 63 123 3 0 34 4 0 Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 16
- 17. OBST CREATION No. of Nodes = 3 : (1,2&3) C[0,3] : i = 0; j =3; k = 1,2,3; k =1 C[0, 1-1] + C[1, 3] = min k=2 C[0, 2-1] + C[2, 3] k=3 + (W1+W2+W3) C[0, 3-1] + C[3, 3] = min k= 1 (0+10) k= 2 (4+6) k= 3 (8+0) = 8 + 12 = 203 Item 1 2 3 4 Key 10 20 30 40 Freq (W) 4 2 6 3 i j 0 1 2 3 4 0 0 41 81 203 1 0 22 103 2 0 63 123 3 0 34 4 0 + (4+2+6) 17
- 18. OBST CREATION No. of Nodes = 3 : (2,3 & 4) C[1,4] : i = 1; j =4; k = 2,3,4; k =2 C[1, 2-1] + C[2, 4] = min k=3 C[1, 3-1] + C[3, 4] k=4 + (W2+W3+W4) C[1, 4-1] + C[4, 4] = min k= 2 (0+12) k= 3 (2+3) k= 4 (10+0) = 5 + 11 = 163 Item 1 2 3 4 Key 10 20 30 40 Freq (W) 4 2 6 3 i j 0 1 2 3 4 0 0 41 81 203 1 0 22 103 163 2 0 63 123 3 0 34 4 0 + (2+6+3) 18
- 19. OBST CREATION No. of Nodes = 4 : (j-i) = 4 (4-0) = 4 = C[0,4] Item 1 2 3 4 Key 10 20 30 40 Freq (W) 4 2 6 3 i j 0 1 2 3 4 0 0 41 81 203 1 0 22 103 163 2 0 63 123 3 0 34 4 0 Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 19
- 20. OBST CREATION No. of Nodes = 4 : (1,2,3 & 4) C[0,4] : i = 0; j =4; k = 1,2,3,4; k=1 C[0, 1-1] + C[1, 4] k =2 C[0, 2-1] + C[2, 4] = min k=3 C[0, 3-1] + C[3, 4] k=4 + (W1+W2+W3+W4) C[0, 4-1] + C[4, 4] = min k=1 (0+16) k= 2 (4+12) k= 3 (8+3) k= 4 (20+0) = 11 + 15 = 263 Item 1 2 3 4 Key 10 20 30 40 Freq (W) 4 2 6 3 i j 0 1 2 3 4 0 0 41 81 203 263 1 0 22 103 163 2 0 63 123 3 0 34 4 0 + (4+2+6+3) 20
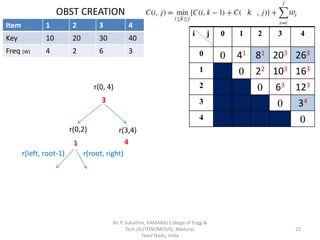
- 21. OBST CREATION Item 1 2 3 4 Key 10 20 30 40 Freq (W) 4 2 6 3 i j 0 1 2 3 4 0 0 41 81 203 263 1 0 22 103 163 2 0 63 123 3 0 34 4 0 r(0, 4) 3 Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 21
- 22. OBST CREATION Item 1 2 3 4 Key 10 20 30 40 Freq (W) 4 2 6 3 i j 0 1 2 3 4 0 0 41 81 203 263 1 0 22 103 163 2 0 63 123 3 0 34 4 0 r(0, 4) 3 r(left, root-1) r(root, right) Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 22
- 23. OBST CREATION Item 1 2 3 4 Key 10 20 30 40 Freq (W) 4 2 6 3 i j 0 1 2 3 4 0 0 41 81 203 263 1 0 22 103 163 2 0 63 123 3 0 34 4 0 r(0, 4) r(0,2) r(3,4) 3 r(left, root-1) r(root, right) Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 23
- 24. OBST CREATION Item 1 2 3 4 Key 10 20 30 40 Freq (W) 4 2 6 3 i j 0 1 2 3 4 0 0 41 81 203 263 1 0 22 103 163 2 0 63 123 3 0 34 4 0 r(0, 4) r(0,2) r(3,4) 3 1 4 Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 24
- 25. OBST CREATION Item 1 2 3 4 Key 10 20 30 40 Freq (W) 4 2 6 3 i j 0 1 2 3 4 0 0 41 81 203 263 1 0 22 103 163 2 0 63 123 3 0 34 4 0 r(0, 4) r(0,2) r(3,4) 3 1 4 r(left, root-1) r(root, right) Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 25
- 26. OBST CREATION Item 1 2 3 4 Key 10 20 30 40 Freq (W) 4 2 6 3 i j 0 1 2 3 4 0 0 41 81 203 263 1 0 22 103 163 2 0 63 123 3 0 34 4 0 r(0, 4) r(0,2) r(3,4) 3 1 4 r(0,0) r(1,2) r(left, root-1) r(root, right) 2 Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 26
- 27. OBST CREATION Item 1 2 3 4 Key 10 20 30 40 Freq (W) 4 2 6 3 i j 0 1 2 3 4 0 0 41 81 203 263 1 0 22 103 163 2 0 63 123 3 0 34 4 0 r(0, 4) r(0,2) r(3,4) 3 1 4 r(0,0) r(1,2) r(left, root-1) r(root, right) 2 Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 27
- 28. OBST CREATION Item 1 2 3 4 Key 10 20 30 40 Freq (W) 4 2 6 3 i j 0 1 2 3 4 0 0 41 81 203 263 1 0 22 103 163 2 0 63 123 3 0 34 4 0 r(0, 4) r(0,2) r(3,4) 3 1 4 r(0,0) r(1,2) r(left, root-1) r(root, right) 2 r(1,1) r(2,2) Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 28
- 29. OBST CREATION Item 1 2 3 4 Key 10 20 30 40 Freq (W) 4 2 6 3 i j 0 1 2 3 4 0 0 41 81 203 263 1 0 22 103 163 2 0 63 123 3 0 34 4 0 r(0, 4) r(0,2) r(3,4) 3 1 4 r(0,0) r(1,2) r(left, root-1) r(root, right) 2 r(1,1) r(2,2) Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 29
- 30. OBST CREATION Item 1 2 3 4 Key 10 20 30 40 Freq (W) 4 2 6 3 i j 0 1 2 3 4 0 0 41 81 203 263 1 0 22 103 163 2 0 63 123 3 0 34 4 0 r(0, 4) r(0,2) r(3,4) 3 1 4 r(0,0) r(1,2) r(left, root-1) r(root, right) 2 r(1,1) r(2,2) Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 30
- 31. OBST CREATION Item 1 2 3 4 Key 10 20 30 40 Freq (W) 4 2 6 3 i j 0 1 2 3 4 0 0 41 81 203 263 1 0 22 103 163 2 0 63 123 3 0 34 4 0 r(0, 4) r(0,2) r(3,4) 3 1 4 r(0,0) r(1,2) r(left, root-1) r(root, right) 2 r(1,1) r(2,2) r(3,3) r(4,4) Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 31
- 32. OBST CREATION Item 1 2 3 4 Key 10 20 30 40 Freq (W) 4 2 6 3 i j 0 1 2 3 4 0 0 41 81 203 263 1 0 22 103 163 2 0 63 123 3 0 34 4 0 r(0, 4) r(0,2) r(3,4) 3 1 4 r(0,0) r(1,2) r(left, root-1) r(root, right) 2 r(1,1) r(2,2) r(3,3) r(4,4) Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 32
- 33. OBST CREATION Item 1 2 3 4 Key 10 20 30 40 Freq (W) 4 2 6 3 i j 0 1 2 3 4 0 0 41 81 203 263 1 0 22 103 163 2 0 63 123 3 0 34 4 0 3 1 4 2 Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 33
- 34. OBST CREATION Item 1 2 3 4 Key 10 20 30 40 Freq (W) 4 2 6 3 i j 0 1 2 3 4 0 0 41 81 203 263 1 0 22 103 163 2 0 63 123 3 0 34 4 0 3 1 4 2 Dr. P. Subathra, KAMARAJ College of Engg & Tech (AUTONOMOUS), Madurai, Tamil Nadu, India 34
- 35. END…!!!