Optimization algorithms for solving computer vision problems
Download as pptx, pdf1 like596 views
The document discusses optimization algorithms for solving computer vision problems. It describes how computer vision problems can be formulated as energy minimization problems over pixel labels. Specific examples of segmentation and depth estimation are provided. Graph cuts is presented as an efficient algorithm for minimizing energies that can be expressed as sums of unary and pairwise terms. The algorithm works by finding the minimum s-t cut in a graph constructed from the energy terms.
![Example 1
Binary segmentation
Labels 𝑓𝑥,𝑦 are black(0) and white (1)
Input image 𝐼 𝑥, 𝑦 𝜖[0..1]
| ∙ | Linear luminance penalty
Regularization
4-pixel neighbourhood
|∙| Linear segment index difference penalty
9
Left Right
Top
Bottom
dx,y
dx,y-1
dx,y+1
dx-1,y dx+1,y
}
Unary terms
Pairwise terms
𝐸 =
𝑥,𝑦
𝐼 𝑥, 𝑦 − 𝑓𝑥,𝑦
+ 𝑓𝑥,𝑦 − 𝑓𝑥+1,𝑦 ∙ 𝛼
+ 𝑓𝑥,𝑦 − 𝑓𝑥−1,𝑦 ∙ 𝛼
+ 𝑓𝑥,𝑦 − 𝑓𝑥,𝑦−1 ∙ 𝛼
+ 𝑓𝑥,𝑦 − 𝑓𝑥,𝑦+1 ∙ 𝛼](https://image.slidesharecdn.com/gc-20150413-1300-170317210914/85/Optimization-algorithms-for-solving-computer-vision-problems-9-320.jpg)
![Minimum s-t cuts
Special nodes
S - Source
T - Sink (Terminal)
Algorithms
Augmenting paths [Ford & Fulkerson, 1962]
Push-relabel [Goldberg-Tarjan, 1986]
14](https://image.slidesharecdn.com/gc-20150413-1300-170317210914/85/Optimization-algorithms-for-solving-computer-vision-problems-14-320.jpg)
Optimization algorithms for solving computer vision problems
- 1. Optimization algorithms for solving computer vision problems Olgierd Stankiewicz Krzysztof Wegner Chair of Multimedia Telecommunications and Microelectronics Poznań University of Technology Poznań, April 2015
- 2. Computer Vision Problems Segmentation Assigning each pixel of the image to a certain segment Depth estimation Assigning a depth value to each pixel of the image 2
- 3. Computer Vision Problems Image stitching Assigning each pixel of the output image to a certain source image (transformed) Image restoration Assigning to each pixel of the output image a colour from the source image 3
- 4. Computer Vision Generalization Can be seen as labeling problem Assigning to each pixel of the output image a label defined in a certain way Label is an index from all possible answers Segment index Disparity Stitched image index Colour 4 1 2 5 5 6 2 1 4 3 5 3 4 4 1 8 3 5 4 0 4 7 2 9 6 7 2 2 4 5 3 6 8 2 1 4 0 0 3 4 3 𝑑 𝑥,𝑦 - label
- 5. Energy minimization There are many ways to label pixels in an image Which one is better? What it the goal? Energy minimalization problem 5 𝐸 𝑓0,0, 𝑓0,1, … , 𝑓 𝑊−1,0, 𝑓1,0, … … 𝑓 𝑊−1,𝐻−1 = 𝑚𝑖𝑛 𝑓𝑥,𝑦 – label for pixel x,y 𝑊, 𝐻 – image size
- 6. Simple? Not simple! Multivariable, e.g. 1920 x 1080 ≈ 2M varables Energy function can be very complex Non-monotonic Non-linear Implicit, with inter-label references Classic Stepest Desent Not too efficient Would probably not find the solution anyway 6
- 7. Efficient minimalization Special class of energy functions can be minimalized more efficiently Energy function decomposed into sum of: Unary terms Pairwise terms Unary and pairwise terms 7 𝐸 = 𝑥,𝑦 𝑈 𝑥,𝑦 𝑓𝑥,𝑦 𝐸 = 𝑥,𝑦,𝑧,𝑤 𝑇𝑥,𝑦,𝑧,𝑤 𝑓𝑥,𝑦, 𝑓𝑧,𝑤
- 8. Efficient minimalization Even more efficient when Binary labeling problem Function argument can be 0 or 1 Energy function is convex (submodular) Triangle inequality E.g. Monotone Linear (Planar etc.) 8 𝑥 + 𝑦 ≤ 𝑥 + |𝑦|
- 9. Example 1 Binary segmentation Labels 𝑓𝑥,𝑦 are black(0) and white (1) Input image 𝐼 𝑥, 𝑦 𝜖[0..1] | ∙ | Linear luminance penalty Regularization 4-pixel neighbourhood |∙| Linear segment index difference penalty 9 Left Right Top Bottom dx,y dx,y-1 dx,y+1 dx-1,y dx+1,y } Unary terms Pairwise terms 𝐸 = 𝑥,𝑦 𝐼 𝑥, 𝑦 − 𝑓𝑥,𝑦 + 𝑓𝑥,𝑦 − 𝑓𝑥+1,𝑦 ∙ 𝛼 + 𝑓𝑥,𝑦 − 𝑓𝑥−1,𝑦 ∙ 𝛼 + 𝑓𝑥,𝑦 − 𝑓𝑥,𝑦−1 ∙ 𝛼 + 𝑓𝑥,𝑦 − 𝑓𝑥,𝑦+1 ∙ 𝛼
- 10. Example 2 Depth estimation Labels 𝑑 𝑥,𝑦 are disparities Image matching between pixels in the left/right image | ∙ | Linear luminance penalty Regularization 4-pixel neighbourhood |∙| Linear disparity difference penalty 10 Left Right Top Bottom dx,y dx,y-1 dx,y+1 dx-1,y dx+1,y } Unary terms Pairwise terms 𝐸 = 𝑥,𝑦 𝐿 𝑥 + 𝑑 𝑥,𝑦, 𝑦 − 𝑅 𝑥, 𝑦 + 𝑑 𝑥,𝑦 − 𝑑 𝑥+1,𝑦 ∙ 𝛼 + 𝑑 𝑥,𝑦 − 𝑑 𝑥−1,𝑦 ∙ 𝛼 + 𝑑 𝑥,𝑦 − 𝑑 𝑥,𝑦−1 ∙ 𝛼 + 𝑑 𝑥,𝑦 − 𝑑 𝑥,𝑦+1 ∙ 𝛼
- 11. Optimization algorithms Viterbi State transitions Well knowm Belief Propagation Message passing Presented before Graph Cuts 11 Node of Markov field, defined by all possible disparities and their probabilities Two-directional connection between nodes of Markov field ........ ........ One-directional connection between nodes of Markov field a) b) each-to-each each-to-each Transition between the states
- 12. Graph Cuts Graph Cuts can be used for efficient unary and pairwise energy minimization Min Cut == Max Flow theorem Solving of Minimal Cut problem in a graph is equal to solving of Maximal Flow problem in the same graph Efficient generic algorithms Expression of energy minimization problem as MinCut 12
- 13. Graphs Nodes Edges Capacity Flow (in a particular solution) Constraints Flow ≤ Capacity Flow conservation E.g. communication network 13
- 14. Minimum s-t cuts Special nodes S - Source T - Sink (Terminal) Algorithms Augmenting paths [Ford & Fulkerson, 1962] Push-relabel [Goldberg-Tarjan, 1986] 14
- 15. Augmenting Paths Find a path from S to T along non-saturated edges Increase flow along this path until some edge saturates 15
- 16. Augmenting Paths Find next path Increase flow 16
- 17. Augmenting Paths Iterate until all paths from S to T have at least one saturated edge 17
- 18. Example Let’s assume a graph Nodes: s,o,p,q,r,t Flow=0 18 s t o p q r sink terminal 0/3 0/3 0/2 0/3 0/2 0/3 0/4 0/2
- 19. Example Path 1, Free Capacity:2 19 s t o p q r sink terminal 0/3 0/3 0/2 0/3 0/2 0/3 0/4 0/2
- 20. Example Path 1, Add Flow:2 20 s t o p q r sink terminal 2/3 0/3 0/2 2/3 2/2 0/3 0/4 0/2
- 21. Example Path 2, Free Capacity:1 21 s t o p q r sink terminal 2/3 0/3 0/2 2/3 2/2 0/3 0/4 0/2
- 22. Example Path 2, Add Flow:1 22 s t o p q r sink terminal 3/3 0/3 0/2 3/3 2/2 1/3 1/4 0/2
- 23. Example Path 3, Free Capacity:0 23 s t o p q r sink terminal 3/3 0/3 0/2 3/3 2/2 1/3 1/4 0/2
- 24. Example Path 4, Free Capacity:2 24 s t o p q r sink terminal 3/3 0/3 0/2 3/3 2/2 1/3 1/4 0/2
- 25. Example Path 4, Add Flow:2 25 s t o p q r sink terminal 3/3 2/3 0/2 3/3 2/2 3/3 1/4 2/2
- 26. Example - flow Flow from sink: 5 = Flow to terminal: 5 Maximal flow = 5 26 s t o p q r sink terminal 3/3 2/3 0/2 3/3 2/2 3/3 1/4 2/2
- 27. Example - cut All possible cuts 27 s t o p q r sink terminal 3 3 2 3 2 3 4 2 6 8 7 10 8 5 5
- 28. Example – minimal cut Minimal Cut = 5 Two equi-optimal cuts 28 s t o p q r sink terminal 3 3 2 3 2 3 4 2 5 5
- 29. Complexity V – number of nodes E – number of edges Augmenting paths 𝑂(𝑉 ∙ 𝐸) via bucket data sorting Kolmogorov 𝑂 𝑉 ∙ 𝐸 Push-relabel 𝑂 𝑉2 𝐸 But parrarelizable 29
- 30. Graph construction 30 min 𝑓1,𝑓2,…,𝑓𝑛−1,𝑓𝑛 𝐸 𝑓1, 𝑓2, … , 𝑓𝑛−1, 𝑓𝑛 𝐸 𝑓1, 𝑓2, … , 𝑓𝑛−1, 𝑓𝑛 = 𝑖 𝐸𝑖 𝑓𝑖 + 𝑖 𝐸𝑖,𝑗 𝑓𝑖, 𝑓𝑗 Each cut throught the graph must represent energy (some potential solution) The graph is a sum of elementary graphs for each energy term
- 31. Graph construction 31 min 𝑓1,𝑓2,…,𝑓𝑛−1,𝑓𝑛 𝐸 𝑓1, 𝑓2, … , 𝑓𝑛−1, 𝑓𝑛 𝐸 𝑓1, 𝑓2, … , 𝑓𝑛−1, 𝑓𝑛 = 𝑖 𝐸𝑖 𝑓𝑖 + 𝑖 𝐸𝑖,𝑗 𝑓𝑖, 𝑓𝑗 𝐸𝑖 1 − 𝐸𝑖 0 𝑓=1s 𝑓=0t 𝐸𝑖 0 − 𝐸𝑖 1 𝑓=1s 𝑓=0t 𝐸𝑖 1 > 𝐸𝑖 0 𝐸𝑖 1 < 𝐸𝑖 0 𝑓𝑖=0 𝑓𝑖=1 𝐸𝑖 𝑓𝑖 2 3 𝑣𝑖 𝑣𝑖
- 32. Graph construction x 32 min 𝑓1,𝑓2,…,𝑓𝑛−1,𝑓𝑛 𝐸 𝑓1, 𝑓2, … , 𝑓𝑛−1, 𝑓𝑛 𝐸 𝑓1, 𝑓2, … , 𝑓𝑛−1, 𝑓𝑛 = 𝑖 𝐸𝑖 𝑓𝑖 + 𝑖 𝐸𝑖,𝑗 𝑓𝑖, 𝑓𝑗 𝐸𝑖,𝑗 1,0 − 𝐸𝑖,𝑗 0,0 𝑓=1s 𝑓=0t 𝑣𝑖 𝑣𝑗 𝐸𝑖,𝑗 1,0 − 𝐸𝑖,𝑗 1,1 𝐸𝑖,𝑗 0,1 + 𝐸𝑖,𝑗 1,0 − 𝐸𝑖,𝑗 0,0 -𝐸𝑖,𝑗 1,1 𝐸𝑖,j 𝑓𝑖, 𝑓𝑗 𝑓j=0 𝑓j=1 𝑓𝑖=0 2 3 𝑓𝑖=1 4 5
- 33. Graph construction 33 𝐸𝑖,j 𝑓𝑖, 𝑓𝑗 𝑓j=0 𝑓j=1 𝑓𝑖=0 𝐸𝑖,j 0,0 𝐸𝑖,j 0,1 𝑓𝑖=1 𝐸𝑖,j 1,0 𝐸𝑖,j 1,1 Assume that 𝐸𝑖,j 0,0 is the biggest 𝐸𝑖,j 0,0 𝐸𝑖,j 0,1 𝐸𝑖,j 1,0 𝐸𝑖,j 1,1 =𝐸𝑖,j 0,0 + 0 𝐸𝑖,j 0,1 -𝐸𝑖,j 0,0 𝐸𝑖,j 1,0 -𝐸𝑖,j 0,0 𝐸𝑖,j 1,1 -𝐸𝑖,j 0,0 =𝐸𝑖,j 0,0 + = 0 0 𝐸𝑖,j 1,0 -𝐸𝑖,j 0,0 𝐸𝑖,j 1,0 -𝐸𝑖,j 0,0 + 0 𝐸𝑖,j 1,1 -𝐸𝑖,j 1,0 0 𝐸𝑖,j 1,1 -𝐸𝑖,j 1,0 + 0 𝐸𝑖,j 0,1 + 𝐸𝑖,j 1,0 − 𝐸𝑖,j 0,0 − 𝐸𝑖,j 1,1 0 0 +
- 34. Graph construction 34 min 𝑓1,𝑓2,…,𝑓𝑛−1,𝑓𝑛 𝐸 𝑓1, 𝑓2, … , 𝑓𝑛−1, 𝑓𝑛 𝐸 𝑓1, 𝑓2, … , 𝑓𝑛−1, 𝑓𝑛 = 𝑖 𝐸𝑖 𝑓𝑖 + 𝑖 𝐸𝑖,𝑗 𝑓𝑖, 𝑓𝑗 𝑓=1s 𝑓=0t 𝑣1 𝑣 𝑛𝑣 𝑛−1𝑣2 𝑣…
- 35. Multilabel energy 𝑓𝑖 can be not only binary Multilabel The are two graphs constructions commonly used Ishikawa multilabel graph Move graph construction 35
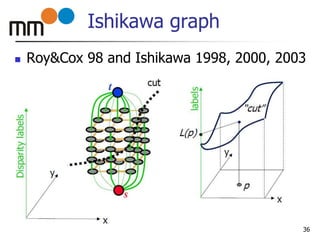
- 36. Ishikawa graph Roy&Cox 98 and Ishikawa 1998, 2000, 2003 36
- 38. Ishikawa graph 38 Many nodes required at once Many edges Very slow Restricted only to linear, pairwise terms
- 39. a-expansion Solves series of binary problems 𝑓𝑖 can be: 0 – keep the current label 1 – change the label to a 39
- 40. a-expansion Start with any* initial solution For each label a in any (e.g. random) order Compute optimal a-expansion move (binary problem) Reject the move if there is no energy decrease Stop when no expansion move would decrease energy 40
- 41. a-expansion Typically two cycles throught all labels are required *Depends on the initial solution At given iteration „some” solution is known In Ishikawa only after solving the whole graph 41
- 42. Thank you for attention Questions? 42