Overview on Optimization algorithms in Deep Learning
- 1. Gradient Descent Optimization Algorithms Van Phu Quang Huy Ta Duc Tung Pham Quang Khang 1
- 2. Topics of today’s talk ● Function optimization ● Basics optimization algorithms and limitation ● Challenges in gradient descent optimization ● Practical gradient descent algorithms 2
- 3. Optimization in Machine learning ● Machine learning cares about performance measure P, that is defined with respect to the test set and may also be intractable ● Learning process: optimize P indirectly by optimizing a cost function J(θ), in the hope that doing so will improve P ● First problem of machine learning: optimization for cost function J(θ) 3
- 5. What is function optimization ● Optimization = minimizing or maximizing ● Maximizing a function f may be accomplished via minimizing -f ● f is called an objective function or criterion ● In the case of minimization, f is also called cost function, loss function, or error function 5
- 6. Optimization Problem ● Example: find extrema of function f(x,y)=x2 +y2 6
- 7. Optimization Problem ● Example: find extrema of function f(x,y)=x2 +y2 ● Easy? 7
- 8. Optimization Problem ● Example: find extrema of function f(x,y)=x2 +y2 ● Easy? ● How about f(x,y)=-x2 -y2 8
- 9. Optimization Problem ● Example: find extrema of function f(x,y)=x2 +y2 ● Easy? ● How about f(x,y)=-x2 -y2 ● Still easy? 9
- 10. Optimization Problem ● Example: find extrema of function f(x,y)=x2 +y2 ● Easy? ● How about f(x,y)=-x2 -y2 ● Still easy? ● How about f(x,y)=x2 -y2 10
- 11. Maxima, minima, and saddle points 11 f(x,y)=x2 +y2 f(x,y)=-x2 -y2 f(x,y)=x2 -y2
- 12. Gradient and the Hessian matrix ● Gradient: vector of first-order partial derivatives 12 ● Hessian: matrix of second-order partial derivatives
- 13. Second Partial Derivative Test f is a multivariate function ● Stationary points: points that make ∇f = 0 ● Second partial derivative test: A stationary point is ○ Local minimum if all eigenvalues of the Hessian positive ○ Local maximum if all eigenvalues of the Hessian negative ○ Saddle point if the Hessian has both positive and negative eigenvalues ○ Inconclusive if the Hessian is invertible 13
- 14. Since H has 2 eigenvalues 1,3 > 0 then (0,0) is a minimum 14 Example: f(x,y) = x2 -xy+y2
- 16. Batch Gradient Descent Blindfolded Hiker: how to get to the lowest place? 16 θ* : Position What we need to find J(θ): Height
- 17. Batch Gradient Descent Blindfolded Hiker: how to get to the lowest place? 17 Go step-by-step ● Which direction? Left or Right? ● How far should I step? Gradient Learning Rate
- 18. Batch Gradient Descent Solution: θ := θ - η∇θ J(θ) 1. Initiate step size η 2. Start with a random point θ 3. Calculate gradient ∇θ J(θ) at point θ 4. Follow the inversed direction of gradient → get new θ 5. Repeat until reach minima a. Stop condition? → gradient is small enough 18
- 19. Batch Gradient Descent Pros ● Stable convergence Cons ● Need to calculate gradient for whole dataset ● Slow if is not implemented wisely 19
- 20. Stochastic Gradient Descent Principle: Same as Batch Gradient Descent Difference: ● Updating θ at each example of training dataset 20 θ := θ - η∇θ J(θ) θ := θ - η∇θ J(θ;x(i) ,y(i) )
- 21. Stochastic Gradient Descent Pros ● Faster than Batch Gradient ● Possible to learn online Cons ● Unstable convergence ● Not use optimized vector operation 21 Image Credit: Pham Quang Khang Fluctuation in Stochastic Gradient Descent
- 22. Optimization in Machine Learning 22
- 23. Example of a cost function ● Example: cross entropy in logistic regression where xn is vector input, yn is label, w is weight matrix, N is number of training examples, σ is sigmoid function ● The shape of the cost function is poorly understood 23
- 24. Convexity problem ● In traditional machine learning, objective functions are designed carefully to be convex ○ Example: objective function of SVM is convex. ● When training neural networks, we must confront the non-convex case ○ Many local minima → infeasible to find global minima ○ Dealing with saddle points ○ Flat regions exist 24
- 25. Local minima ● In practice, local minima is not a major problem ● [1] gives some theoretical insights about local minima: ○ For large-size networks, most local minima are equivalent and yield similar performance on a test set ○ The probability of finding a “bad” (high value) local minimum is non-zero for small-size networks and decreases quickly with network size ○ Struggling to find the global minimum on the training set (as opposed to one of the many good local ones) is not useful in practice and may lead to overfitting 25[1] Choromanska et al. 2014.
- 26. Saddle points ● For high-dimensional non-convex functions, saddle points are much more than local minima (and maxima) [1] ● Saddle points slow down training process ○ Batch Gradient Descent may be stuck at saddle points ○ Stochastic Gradient Descent seems to be able to escape saddle points in many cases [2] 26 [1] Dauphin et al. 2014. [2] Goodfellow et al. 2015.
- 27. Flat regions ● Flat regions: regions of constant value, where the gradient and the Hessian are both 0 ● Big problem when those regions have high value of the objective function ● Escaping from those regions is extremely difficult 27y = x5
- 28. ● At (0,0) the gradient and the Hessian are both 0 → f is super flat at (0,0) ● Second partial derivative test can’t determine whether (0,0) is a local minimum, a local maximum or a saddle point ● In this case, (0,0) is a global maximum 28 Flat regions: example of cost function f(x,y) = -x2 y2
- 29. Flat regions: example of cost function f(x,y) = xy(x+y)(1+y) ● At (0,0) the gradient and the Hessian are both 0 too ● But in this case, (0,0) is a saddle point 29
- 30. Practical Gradient Descent Algorithms 30
- 31. Gradient descent optimization problem ● Objective: to find the parameters θ that minimize the lost function J(θ) ● Approach: iteratively update the params θ by utilizing the gradient ∇J(θ) ● Gradient descent conventional method: θt = θt-1 - η∇J(θ) 31
- 32. Momentum ● Add momentum to params updater: vt = αvt-1 - η∇J(θt-1 ) θt = θt-1 + vt ● Essential meaning of Momentum: ○ Accelerate the learning rate during the training process ○ In physic: add the momentum to the ball that rolling down the hill ○ The momentum parameter α is less than 1 as there is always resistance force to slow the ball down and usually picked as 0.9 32
- 33. Adaptive learning rate ● Previous algorithm always use the fixed learning rate throughout the learning process ○ The learning rate has to be either set to be very small at the beginning or periodically decrease the learning rate ● Adaptive learning rate: learning rate is automatically decreased in the learning process ● Adaptive learning rate algo: AdaGrad, RMSprop, Adam 33
- 34. Adagrad ● Essential meaning: the larger the params change the slower it get updated ● Algorithms: Accumulated sum-square ht = ht-1 + ∇J(θt-1 )・∇J(θt-1 ) Params updater θt = θt-1 - η(1/sqrt(ht ))・∇J(θ) ● The learning rate is decreased as the number of update step increases 34
- 35. RMSprop ● Adagrad decreases the learning rate too fast as it adds all previous square gradients ● Consider partially previous added up sum square gradient: Accumulated sum-square ht = γht-1 + (1-γ)∇J(θt-1 )・∇J(θt-1 ) Params updater θt = θt-1 - η(1/sqrt(ht ))・∇J(θt-1 ) ● Good practice γ = 0.9 35
- 36. Adam (Adaptive momentum estimation) ● Utilizing the advantage of both Momentum and Adagrad ● Algorithm Momentum: vt = β1 vt-1 + (1 - β1 )∇J(θt-1 ) Learning rate: ht = β2 ht-1 + (1 - β2 )∇J(θt-1 )・∇J(θt-1 ) To avoid momentum and learning rate decay to be too small, zero-bias counteract is calculated: Vt ’ = vt /(1 - β1 t ), ht ’ = ht /(1 - β2 t ) Param update: θt = θt-1 - ηVt ’/(sqrt(ht ’) + ε) 36
- 37. Compare all 4 algorithms +SGD on benchmark data ● Data: part of MNIST ● Input size: 28x28x1, output size: 10 ● Model: NN with 4 hidden layers, 100 units each layer ● Train data number: 800, test data number: 200 ● Batch size: 100 ● Number of epoch: 1000 ● Initial weight: Ɲ(0, 0.1) 37
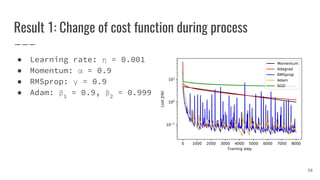
- 38. Result 1: Change of cost function during process ● Learning rate: η = 0.001 ● Momentum: α = 0.9 ● RMSprop: γ = 0.9 ● Adam: β1 = 0.9, β2 = 0.999 38
- 39. Result 2: Accuracy of training Training set 39 Test set
- 40. Simple CNN test ● Conv - pool - fully connected - softmax ● Conv params: ○ Filter number: 30 ○ Filter size: 5x5x1 ○ Pad: 0 ○ Stride: 1 ● Input size: 28x28x1, output size: 10 ● Train data: 800, test: 200 ● Number epoch: 50 ● FC layer size: 100 40
- 41. Simple CNN result1: cost function ● Learning rate: η = 0.001 ● Momentum: α = 0.9 ● RMSProp: γ = 0.9 ● Adam: β1 = 0.9, β2 = 0.999 41
- 42. Simple CNN result 2: accuracy Train 42 Test
- 43. References 43
- 44. Machine Learning Definition "A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P if its performance at tasks in T, as measured by P, improves with experience E." [1] [1] Mitchell, T. (1997). Machine Learning. McGraw Hill. p2. 44
- 45. Exploding Gradients ● Cliffs: where the gradient is super big ● One update step of gradient descent can move the parameters extremely far, usually over the minimum point ● Solution: gradient clipping 45 Goodfellow et al, Deep Learning book, p289
- 46. Vanishing Gradients ● Is a major problem when training deep networks ● The gradient tends to get smaller as we move backward through the hidden layers when running backpropagation ● Weights in the earlier layers may not be learned ● Solutions: ○ Use good activation functions (e.g. ReLU) instead of sigmoid ○ Good initialization ○ Better network architectures (LSTMs/GRUs instead of basic RNNs) 46
- 47. Sharp and Wide Minima [1] ● Large-batch Gradient Descent tends to converge to sharp minima → poorer generalization ● Small-batch Gradient Descent consistently converges to wide minima → better generalization 47[1] Keskar et al. 2017.

























![Local minima
● In practice, local minima is not a major problem
● [1] gives some theoretical insights about local minima:
○ For large-size networks, most local minima are equivalent and yield
similar performance on a test set
○ The probability of finding a “bad” (high value) local minimum is
non-zero for small-size networks and decreases quickly with network
size
○ Struggling to find the global minimum on the training set (as opposed
to one of the many good local ones) is not useful in practice and may
lead to overfitting
25[1] Choromanska et al. 2014.](https://image.slidesharecdn.com/optimizationalgorithms-170625041750/85/Overview-on-Optimization-algorithms-in-Deep-Learning-25-320.jpg)
![Saddle points
● For high-dimensional non-convex functions, saddle points
are much more than local minima (and maxima) [1]
● Saddle points slow down training process
○ Batch Gradient Descent may be stuck at saddle points
○ Stochastic Gradient Descent seems to be able to escape saddle points
in many cases [2]
26
[1] Dauphin et al. 2014.
[2] Goodfellow et al. 2015.](https://image.slidesharecdn.com/optimizationalgorithms-170625041750/85/Overview-on-Optimization-algorithms-in-Deep-Learning-26-320.jpg)
















![Machine Learning Definition
"A computer program is said to learn from experience E with
respect to some class of tasks T and performance measure P
if its performance at tasks in T, as measured by P, improves
with experience E." [1]
[1] Mitchell, T. (1997). Machine Learning. McGraw Hill. p2.
44](https://image.slidesharecdn.com/optimizationalgorithms-170625041750/85/Overview-on-Optimization-algorithms-in-Deep-Learning-44-320.jpg)


![Sharp and Wide Minima [1]
● Large-batch Gradient Descent tends to converge to sharp minima
→ poorer generalization
● Small-batch Gradient Descent consistently converges to wide minima
→ better generalization
47[1] Keskar et al. 2017.](https://image.slidesharecdn.com/optimizationalgorithms-170625041750/85/Overview-on-Optimization-algorithms-in-Deep-Learning-47-320.jpg)