Selection sort algorithm presentation, selection sort example using power point

Sep 14, 2018Download as pptx, pdf

2 likes1,078 views

University of Science and Technology Chitttagong

The slide was made for computer science student who try to easily understand selection by a easy example. if u need u can watch it.

Selection sort algorithm presentation, selection sort example using power point

#Presentation submitted to:
Sohrab Hossain, Assistant professor of CSE
FSET,USTC
#Presentation submitted by:
Md Abdul Kuddus
Department of CSE
ID:15010102
Batch:25th

#Presentation Name:
Write a program to sort the element of
an array using selection sort.
#What is selection sort??
 Repeatedly searches for the largest value in a section of the
data
 Moves that value into its correct position in a sorted
section of the list
 Uses the Find Largest algorithm

#Example:
Given array: 34 8 64 51 32 21
sorted comparison item unsorted
comparison time
0 1 2 3 4 5

Most read

#source code:
#include <stdio.h>
int *selectionSort(int A[],int n)
{
int j ,k ,temp;
for (k= 0; k < n; k++)
{
for(j = k+1; j < n; j++)
{
if(A[k] > A[j])
{
temp = A[k];
A[k] = A[j];
A[j] = temp;
}
}
}
return A;
}

int main()
{
int A[1000],k,n;
printf("Enter the number of element you want to Sort : ");
scanf("%d",&n);
printf("Enter Elements in the list : ");
for(k = 0; k < n; k++)
{
scanf("%d",&A[k]);
}
int *sortArray = selectionSort(A,n);
printf("Sorted list : ");
for(k = 0; k < n; k++ )
{
printf("%dt",sortArray[k]);
}
}

#Time efficiency
 Comparisons: n(n-1)/2
 Exchanges: n (swapping largest into place)
 Overall: (n2), best and worst cases
#Space efficiency
 Space for the input sequence, plus a constant number of local
variables

*pass 1: compare 1st position with minimum item
After pass1
*pass2: compare 2nd position with next minimum item
After pass2
34 8 64 51 21
8
34 64 51 218
34 64 51 21
8 21 64 51 34

*pass3: compare 3rd position with next minimum item
After pass3
*pass4: compare 4th position with next minimum item
After pass4
Array is sorted
8 21 64 51 34
8 21 34 51 64
8 21 34 51 64
8 21 34 51 64

*Algorithm:
Algorithm SELECTION(A,N)
Step1 : Repeat steps 2 and 3 for k=1,2,….N-1;
Step2 : Call MIN(A,K,N,LOC).
Step3: [Interchange A[k] and A[LOC].]
Set TEMP:=A[k],
A[k]:=A[LOC] and
A[LOC]:=TEMP.
[End of step 1 loop]
Step4:Exit.

Selection sort is a sorting algorithm that works by repeatedly finding the minimum element from an unsorted sublist and putting it at the front. It has the following steps: 1. Start with an unsorted list. 2. Find the minimum element in the list and swap it with the first element. 3. Repeat step 2 for the remaining elements, each time considering one less element at the front that is already in sorted order. The algorithm runs in O(n2) time as the inner loop needs to run n-1 times for n elements. It works for both ascending and descending order by changing the comparison operator in the inner loop.

Presentation on the topic selection sortDistrict Administration

The document presents an overview of selection sort, including its definition, algorithm, example, advantages, and disadvantages. Selection sort works by iteratively finding the minimum element in an unsorted sublist and exchanging it with the first element. It has a time complexity of O(n2) but performs well on small lists since it is an in-place sorting algorithm with minimal additional storage requirements. However, it is not efficient for huge datasets due to its quadratic time complexity.

Merge sort algorithmShubham Dwivedi

Insertion sortalmaqboli

Insertion sort works by iterating through an array, inserting each element into its sorted position by shifting other elements over. It finds the location where each element should be inserted into the sorted portion using a linear search, moving larger elements out of the way to make room. This sorting algorithm is most effective for small data sets and can be implemented recursively or iteratively through comparisons and shifts.

Quick sort algorithnKumar

- Quicksort is a simple and fast sorting algorithm that can sort arrays "in place" without using extra space. - It works by recursively partitioning the array around a pivot value, sorting the left and right subarrays, and then combining them. - On average, it has a runtime of O(n log n) but in the worst case of an already sorted array it can have a quadratic runtime of O(n^2) like bubble sort. However, its randomized choice of pivots means it rarely encounters worst-case inputs in practice.

Quick Sort , Merge Sort , Heap SortMohammed Hussein

The document discusses various sorting algorithms that use the divide-and-conquer approach, including quicksort, mergesort, and heapsort. It provides examples of how each algorithm works by recursively dividing problems into subproblems until a base case is reached. Code implementations and pseudocode are presented for key steps like partitioning arrays in quicksort, merging sorted subarrays in mergesort, and adding and removing elements from a heap data structure in heapsort. The algorithms are compared in terms of their time and space complexity and best uses.

Prefix, Infix and Post-fix NotationsAfaq Mansoor Khan

Sorting AlgorithmsMohammed Hussein

This document discusses different sorting algorithms including bubble sort, insertion sort, and selection sort. It provides details on each algorithm, including time complexity, code examples, and graphical examples. Bubble sort is an O(n2) algorithm that works by repeatedly comparing and swapping adjacent elements. Insertion sort also has O(n2) time complexity but is more efficient than bubble sort for small or partially sorted lists. Selection sort finds the minimum value and swaps it into place at each step.

SORTING techniques.pptxDr.Shweta

Sorting in data structures is a fundamental operation that is crucial for optimizing the efficiency of data retrieval and manipulation. By ordering data elements according to a defined sequence (numerical, lexicographical, etc.), sorting makes it possible to search for elements more quickly than would be possible in an unsorted structure, especially with algorithms like binary search that rely on a sorted array to operate effectively. In addition, sorting is essential for tasks that require an ordered dataset, such as finding median values, generating frequency counts, or performing range queries. It also lays the groundwork for more complex operations, such as merging datasets, which requires sorted data to be carried out efficiently.

linked lists in data structuresDurgaDeviCbit

Insertion SortingFarihaHabib123

The document describes insertion sort, a sorting algorithm. It lists the group members who researched insertion sort and provides an introduction. It then explains how insertion sort works by example, showing how it iterates through an array and inserts elements into the sorted portion. Pseudocode and analysis of insertion sort's runtime is provided. Comparisons are made between insertion sort and other algorithms like bubble sort, selection sort, and merge sort, analyzing their time complexities in best, average, and worst cases.

Quick sortJehat Hassan

The document provides an overview of the quick sort algorithm through diagrams and explanations. It begins by introducing quick sort and stating that it is one of the fastest sorting algorithms because it runs in O(n log n) time and uses less memory than other algorithms like merge sort. It then provides step-by-step examples to demonstrate how quick sort works by picking a pivot element, partitioning the array around the pivot, and recursively sorting the subarrays. The summary concludes by restating that quick sort is an efficient sorting algorithm due to its speed and memory usage.

sparse matrix in data structureMAHALAKSHMI P

This document discusses sparse matrices. It defines a sparse matrix as a matrix with more zero values than non-zero values. Sparse matrices can save space by only storing the non-zero elements and their indices rather than allocating space for all elements. Two common representations for sparse matrices are the triplet representation, which stores the non-zero values and their row and column indices, and the linked representation, which connects the non-zero elements. Applications of sparse matrices include solving large systems of equations.

Queue data structureanooppjoseph

Hashing Technique In Data StructuresSHAKOOR AB

This document discusses different searching methods like sequential, binary, and hashing. It defines searching as finding an element within a list. Sequential search searches lists sequentially until the element is found or the end is reached, with efficiency of O(n) in worst case. Binary search works on sorted arrays by eliminating half of remaining elements at each step, with efficiency of O(log n). Hashing maps keys to table positions using a hash function, allowing searches, inserts and deletes in O(1) time on average. Good hash functions uniformly distribute keys and generate different hashes for similar keys.

Stacks in c++Vineeta Garg

The document discusses stacks in C++. It defines a stack as a data structure that follows LIFO (Last In First Out) principle where the last element added is the first to be removed. Stacks can be implemented using arrays or linked lists. The key operations on a stack are push which adds an element and pop which removes an element. Example applications of stacks include function call stacks, converting infix to postfix notation, and reversing arrays.

StackSeema Sharma

This document discusses stacks and their applications. It defines a stack as a Last In First Out (LIFO) data structure where newly added items are placed on top. The core stack operations of PUSH, POP, and PEEK are described. An array implementation of stacks is presented and animations demonstrate push and pop operations. Applications of stacks like checking for balanced braces, converting infix to postfix notation, and postfix calculators are explained with examples. Pseudocode provides an algorithm for infix to postfix conversion using a stack.

Priority Queue in Data StructureMeghaj Mallick

This document discusses priority queues. It defines a priority queue as a queue where insertion and deletion are based on some priority property. Items with higher priority are removed before lower priority items. There are two main types: ascending priority queues remove the smallest item, while descending priority queues remove the largest item. Priority queues are useful for scheduling jobs in operating systems, where real-time jobs have highest priority and are scheduled first. They are also used in network communication to manage limited bandwidth.

Ppt bubble sortprabhakar jalasutram

The document describes the bubble sort algorithm. It takes an array of numbers as input, such as {1,3,5,2,4,6}, and sorts it in ascending order through multiple passes where adjacent elements are compared and swapped if in the wrong order, resulting in the sorted array {1,2,3,4,5,6}. The algorithm works by making multiple passes through the array, swapping adjacent elements that are out of order on each pass until the array is fully sorted.

PPT On Sorting And Searching Concepts In Data Structure | In Programming Lang...Umesh Kumar

The document discusses various sorting and searching algorithms: - Bubble sort, selection sort, merge sort, quicksort are sorting algorithms that arrange data in a particular order like numerical or alphabetical. - Linear search and binary search are searching algorithms where linear search sequentially checks each item while binary search divides the data set in half with each comparison. - Examples are provided to illustrate how each algorithm works step-by-step on sample data sets.

Insertion sort bubble sort selection sortUmmar Hayat

The document discusses three sorting algorithms: insertion sort, bubble sort, and selection sort. Insertion sort has best-case linear time but worst-case quadratic time, sorting elements in place. Bubble sort repeatedly compares and swaps adjacent elements, having quadratic time in all cases. Selection sort finds the minimum element and exchanges it into the sorted portion of the array in each pass, with quadratic time.

Searching and sortingPoojithaBollikonda

Insertion sort algorithm power point presentation University of Science and Technology Chitttagong

Insertion sort Monalisa Patel

This document discusses insertion sort, including its mechanism, algorithm, runtime analysis, advantages, and disadvantages. Insertion sort works by iterating through an unsorted array and inserting each element into its sorted position by shifting other elements over. Its worst case runtime is O(n^2) when the array is reverse sorted, but it performs well on small, nearly sorted lists. While simple to implement, insertion sort is inefficient for large datasets compared to other algorithms.

Linked List, Types of Linked LIst, Various Operations, Applications of Linked...Balwant Gorad

Sorting algorithmsTrupti Agrawal

The document discusses various sorting algorithms. It describes how sorting algorithms arrange elements of a list in a certain order. Efficient sorting is important as a subroutine for algorithms that require sorted input, such as search and merge algorithms. Common sorting algorithms covered include insertion sort, selection sort, bubble sort, merge sort, and quicksort. Quicksort is highlighted as an efficient divide and conquer algorithm that recursively partitions elements around a pivot point.

Data Types - Premetive and Non Premetive Raj Naik

This document discusses data types in C programming. It describes primitive data types like integers, floats, characters and their syntax. It also covers non-primitive data types like arrays, structures, unions, and linked lists. Arrays store a collection of similar data types, structures group different data types, and unions store different types in the same memory location. Linked lists are dynamic data structures using pointers. The document also provides overviews of stacks and queues, describing their LIFO and FIFO properties respectively.

Data structuresSneha Chopra

This document provides an overview of different data structures and sorting algorithms. It begins with an introduction to data structures and describes linear data structures like arrays, stacks, queues, and linked lists as well as non-linear data structures like trees and graphs. It then provides more detailed descriptions of stacks, queues, linked lists, and common sorting algorithms like selection sort and bubble sort.

Data structure using c module 3smruti sarangi

DSA-sortijejjejjdjjdjdjjsjsjsjsjsjsjng.pptxsuryatom5775

More Related Content

What's hot (20)

SORTING techniques.pptxDr.Shweta

linked lists in data structuresDurgaDeviCbit

Insertion SortingFarihaHabib123

Quick sortJehat Hassan

sparse matrix in data structureMAHALAKSHMI P

Queue data structureanooppjoseph

Hashing Technique In Data StructuresSHAKOOR AB

Stacks in c++Vineeta Garg

StackSeema Sharma

Priority Queue in Data StructureMeghaj Mallick

Ppt bubble sortprabhakar jalasutram

PPT On Sorting And Searching Concepts In Data Structure | In Programming Lang...Umesh Kumar

Insertion sort bubble sort selection sortUmmar Hayat

Searching and sortingPoojithaBollikonda

Insertion sort algorithm power point presentation University of Science and Technology Chitttagong

Insertion sort Monalisa Patel

Linked List, Types of Linked LIst, Various Operations, Applications of Linked...Balwant Gorad

Sorting algorithmsTrupti Agrawal

Data Types - Premetive and Non Premetive Raj Naik

Data structuresSneha Chopra

SORTING techniques.pptxDr.Shweta

linked lists in data structuresDurgaDeviCbit

Insertion SortingFarihaHabib123

Quick sortJehat Hassan

sparse matrix in data structureMAHALAKSHMI P

Queue data structureanooppjoseph

Hashing Technique In Data StructuresSHAKOOR AB

Stacks in c++Vineeta Garg

StackSeema Sharma

Priority Queue in Data StructureMeghaj Mallick

Ppt bubble sortprabhakar jalasutram

PPT On Sorting And Searching Concepts In Data Structure | In Programming Lang...Umesh Kumar

Insertion sort bubble sort selection sortUmmar Hayat

Searching and sortingPoojithaBollikonda

Insertion sort algorithm power point presentation University of Science and Technology Chitttagong

Insertion sort Monalisa Patel

Linked List, Types of Linked LIst, Various Operations, Applications of Linked...Balwant Gorad

Sorting algorithmsTrupti Agrawal

Data Types - Premetive and Non Premetive Raj Naik

Data structuresSneha Chopra

Similar to Selection sort algorithm presentation, selection sort example using power point (20)

Data structure using c module 3smruti sarangi

DSA-sortijejjejjdjjdjdjjsjsjsjsjsjsjng.pptxsuryatom5775

Searching_Sorting.pptx21BD1A058RSahithi

The document provides information about different searching and sorting algorithms. It defines linear search and binary search as two common searching methods. Linear search sequentially checks each element until a match is found, while binary search can only be used on a sorted list and successively divides the list in half. The document also describes selection sort, bubble sort, and insertion sort sorting algorithms. Selection sort finds the minimum element and swaps it into position, bubble sort compares and swaps adjacent elements, and insertion sort inserts elements into the sorted position.

Insertion sortDelowar Hossain

The document presents information on insertion sort, including: - Insertion sort works by partitioning an array into sorted and unsorted portions, iteratively finding the correct insertion point for elements in the unsorted portion and shifting other elements over to make space. - The insertion sort algorithm uses a nested loop structure to iterate through the array, comparing elements and shifting them if needed to insert the current element in the proper sorted position. - The time complexity of insertion sort is O(n^2) in the worst case when the array is reverse sorted, requiring up to n(n-1)/2 comparisons and shifts, but it is O(n) in the best case of a presorted array. On average,

Chapter 3 - Elementary Searching and Sorting Algorithms.pptAbdisaAwel

CHAP 3 ALGORITHM for infomatique ingenieure .pptFarahHarrathi1

Unit III Version I.pptxssuserd602fd

The document discusses various sorting and searching algorithms. It begins by introducing selection sort, insertion sort, and bubble sort. It then covers merge sort and explains how it works by dividing the list, sorting sublists recursively, and merging the results. Finally, it discusses linear/sequential search and binary search, noting that sequential search checks every element while binary search repeatedly halves the search space.

lecture-k-sorting.pptSushantRaj25

3.pptganeshyadav184128

Lecture k-sortingVijayaraj Raj

The document outlines different sorting algorithms including selection sort, bubble sort, insertion sort, shell sort, merge sort, and quicksort. It discusses how to use the standard sorting methods in Java's API and provides pseudocode and examples of implementing selection sort, bubble sort, insertion sort, and merge sort. It analyzes the time complexity of these algorithms and discusses which are best for small, medium, and large arrays.

Sorting and Searching TechniquesProf Ansari

Searching Information retrieval in the required format is the common activity in all computer applications. This involves searching, sorting and merging. Searching methods are designed to take advantage of the file organization and optimize the search for a particular record or establish its absence. Sequential Search The simplest technique for searching an unordered table for a particular record is to scan each entry in the table in a sequential manner until the desired record is found. This is the most natural way of searching. In this method, we simply go through a list or a file till the required record is found or end of list or file is encountered. Ordering of list is not important

lecture to proide studeny with F-k-sorting.pptindranilbanerji25109

advanced searching and sorting.pdfharamaya university

Data Structures_ Sorting & SearchingThenmozhiK5

The document discusses various searching and sorting algorithms. It begins by defining searching as finding an item in a list. It describes sequential and binary search techniques. For sorting, it covers bubble, selection, insertion, merge, quick and heap sorts. It provides pseudocode examples and analyzes the time complexity of algorithms like selection sort and quicksort. Key aspects covered include the divide and conquer approach of quicksort and the efficiency of various sorting methods.

DS - Unit 2 FINAL (2).pptxprakashvs7

Chapter3.pptxASMAALWADEE2

Searching and sorting Techniques in Data structuresPRIANKA R

Sorting and hashing conceptsLJ Projects

Sorting arranges data in a specific order by comparing elements according to a key value. The main sorting methods are bubble sort, selection sort, insertion sort, quicksort, mergesort, heapsort, and radix sort. Hashing maps data to table indexes using a hash function to provide direct access, with the potential for collisions. Common hash functions include division, mid-square, and folding methods.

Sorting and hashing conceptsLJ Projects

Address calculation-sortVasim Pathan

Bucket sort is a distribution sorting algorithm that works by distributing elements of an array into buckets. It then sorts the elements within each bucket using a simpler sorting algorithm like insertion sort. The sorted buckets are then concatenated together to produce the final sorted array. Radix sort is a multiple pass sorting algorithm that distributes elements into buckets based on the value of each digit of the key. It processes keys digit-by-digit until the array is fully sorted. Address calculation sort uses a hash function to distribute elements into buckets (subfiles) based on the result of the hash function applied to each key. Elements are inserted into the buckets and sorted within using another sorting algorithm like insertion sort before concatenating the buckets to get the final sorted list

Data structure using c module 3smruti sarangi

DSA-sortijejjejjdjjdjdjjsjsjsjsjsjsjng.pptxsuryatom5775

Searching_Sorting.pptx21BD1A058RSahithi

Insertion sortDelowar Hossain

Chapter 3 - Elementary Searching and Sorting Algorithms.pptAbdisaAwel

CHAP 3 ALGORITHM for infomatique ingenieure .pptFarahHarrathi1

Unit III Version I.pptxssuserd602fd

lecture-k-sorting.pptSushantRaj25

3.pptganeshyadav184128

Lecture k-sortingVijayaraj Raj

Sorting and Searching TechniquesProf Ansari

lecture to proide studeny with F-k-sorting.pptindranilbanerji25109

advanced searching and sorting.pdfharamaya university

Data Structures_ Sorting & SearchingThenmozhiK5

DS - Unit 2 FINAL (2).pptxprakashvs7

Chapter3.pptxASMAALWADEE2

Searching and sorting Techniques in Data structuresPRIANKA R

Sorting and hashing conceptsLJ Projects

Address calculation-sortVasim Pathan

Recently uploaded (20)

Engineering Mechanics Introduction and its ApplicationSakthivel M

Flow Chart Proses Bisnis prosscesss.docxrifka575530

Great power lithium iron phosphate cellssalmankhan835951

Rearchitecturing a 9-year-old legacy Laravel application.pdfTakumi Amitani

An initiative to re-architect a Laravel legacy application that had been running for 9 years using the following approaches, with the goal of improving the system’s modifiability: ・Event Storming ・Use Case Driven Object Modeling ・Domain Driven Design ・Modular Monolith ・Clean Architecture This slide was used in PHPxTKY June 2025. https://phpxtky.connpass.com/event/352685/

最新版美国圣莫尼卡学院毕业证（SMC毕业证书）原版定制Taqyea

鉴于此，定制圣莫尼卡学院学位证书提升履历【q薇1954292140】原版高仿圣莫尼卡学院毕业证(SMC毕业证书)可先看成品样本【q薇1954292140】帮您解决在美国圣莫尼卡学院未毕业难题，美国毕业证购买，美国文凭购买，【q微1954292140】美国文凭购买，美国文凭定制，美国文凭补办。专业在线定制美国大学文凭，定做美国本科文凭，【q微1954292140】复制美国Santa Monica College completion letter。在线快速补办美国本科毕业证、硕士文凭证书，购买美国学位证、圣莫尼卡学院Offer，美国大学文凭在线购买。如果您处于以下几种情况： ◇在校期间，因各种原因未能顺利毕业……拿不到官方毕业证 ◇面对父母的压力，希望尽快拿到； ◇不清楚认证流程以及材料该如何准备； ◇回国时间很长，忘记办理； ◇回国马上就要找工作，办给用人单位看； ◇企事业单位必须要求办理的 ◇需要报考公务员、购买免税车、落转户口 ◇申请留学生创业基金【复刻一套圣莫尼卡学院毕业证成绩单信封等材料最强攻略,Buy Santa Monica College Transcripts】购买日韩成绩单、英国大学成绩单、美国大学成绩单、澳洲大学成绩单、加拿大大学成绩单（q微1954292140）新加坡大学成绩单、新西兰大学成绩单、爱尔兰成绩单、西班牙成绩单、德国成绩单。成绩单的意义主要体现在证明学习能力、评估学术背景、展示综合素质、提高录取率，以及是作为留信认证申请材料的一部分。圣莫尼卡学院成绩单能够体现您的的学习能力，包括圣莫尼卡学院课程成绩、专业能力、研究能力。（q微1954292140）具体来说，成绩报告单通常包含学生的学习技能与习惯、各科成绩以及老师评语等部分，因此，成绩单不仅是学生学术能力的证明，也是评估学生是否适合某个教育项目的重要依据！

02 - Ethics & Professionalism - BEM, IEM, MySET.PPTSharinAbGhani1

362 Alec Data Center Solutions-Slysium Data Center-AUH-ABB Furse.pdfdjiceramil

362 Alec Data Center Solutions-Slysium Data Center-AUH-Adaptaflex.pdfdjiceramil

Rigor, ethics, wellbeing and resilience in the ICT doctoral journeyYannis

The doctoral thesis trajectory has been often characterized as a “long and windy road” or a journey to “Ithaka”, suggesting the promises and challenges of this journey of initiation to research. The doctoral candidates need to complete such journey (i) preserving and even enhancing their wellbeing, (ii) overcoming the many challenges through resilience, while keeping (iii) high standards of ethics and (iv) scientific rigor. This talk will provide a personal account of lessons learnt and recommendations from a senior researcher over his 30+ years of doctoral supervision and care for doctoral students. Specific attention will be paid on the special features of the (i) interdisciplinary doctoral research that involves Information and Communications Technologies (ICT) and other scientific traditions, and (ii) the challenges faced in the complex technological and research landscape dominated by Artificial Intelligence.

chemistry investigatory project for class 12Susis10

Water demand - Types , variations and WDSdhanashree78

社内勉強会資料_Chain of Thought .NABLAS株式会社

本資料「To CoT or not to CoT?」では、大規模言語モデルにおけるChain of Thought（CoT）プロンプトの効果について詳しく解説しています。 CoTはあらゆるタスクに効く万能な手法ではなく、特に数学的・論理的・アルゴリズム的な推論を伴う課題で高い効果を発揮することが実験から示されています。一方で、常識や一般知識を問う問題に対しては効果が限定的であることも明らかになりました。複雑な問題を段階的に分解・実行する「計画と実行」のプロセスにおいて、CoTの強みが活かされる点も注目ポイントです。 This presentation explores when Chain of Thought (CoT) prompting is truly effective in large language models. The findings show that CoT significantly improves performance on tasks involving mathematical or logical reasoning, while its impact is limited on general knowledge or commonsense tasks.

SEW make Brake BE05 – BE30 Brake – Repair Kitprojectultramechanix

TEA2016AAT 160 W TV application design examplessuser1be9ce

operationg systemsdocumentmemorymanagementSNIGDHAAPPANABHOTLA

362 Alec Data Center Solutions-Slysium Data Center-AUH-Glands & Lugs, Simplex...djiceramil

IntroSlides-June-GDG-Cloud-Munich community gathering@Netlight.pdf

IntroSlides-June-GDG-Cloud-Munich community [email protected]Luiz Carneiro

A Comprehensive Investigation into the Accuracy of Soft Computing Tools for D...Journal of Soft Computing in Civil Engineering

This study will provide the audience with an understanding of the capabilities of soft tools such as Artificial Neural Networks (ANN), Support Vector Regression (SVR), Model Trees (MT), and Multi-Gene Genetic Programming (MGGP) as a statistical downscaling tool. Many projects are underway around the world to downscale the data from Global Climate Models (GCM). The majority of the statistical tools have a lengthy downscaling pipeline to follow. To improve its accuracy, the GCM data is re-gridded according to the grid points of the observed data, standardized, and, sometimes, bias-removal is required. The current work suggests that future precipitation can be predicted by using precipitation data from the nearest four grid points as input to soft tools and observed precipitation as output. This research aims to estimate precipitation trends in the near future (2021-2050), using 5 GCMs, for Pune, in the state of Maharashtra, India. The findings indicate that each one of the soft tools can model the precipitation with excellent accuracy as compared to the traditional method of Distribution Based Scaling (DBS). The results show that ANN models appear to give the best results, followed by MT, then MGGP, and finally SVR. This work is one of a kind in that it provides insights into the changing monsoon season in Pune. The anticipated average precipitation levels depict a rise of 300–500% in January, along with increases of 200-300% in February and March, and a 100-150% increase for April and December. In contrast, rainfall appears to be decreasing by 20-30% between June and September.

grade 9 science q1 quiz.pptx science quiznorfapangolima

22PCOAM16 _ML_Unit 3 Notes & Question bankGuru Nanak Technical Institutions

Engineering Mechanics Introduction and its ApplicationSakthivel M

Flow Chart Proses Bisnis prosscesss.docxrifka575530

Great power lithium iron phosphate cellssalmankhan835951

Rearchitecturing a 9-year-old legacy Laravel application.pdfTakumi Amitani

最新版美国圣莫尼卡学院毕业证（SMC毕业证书）原版定制Taqyea

02 - Ethics & Professionalism - BEM, IEM, MySET.PPTSharinAbGhani1

362 Alec Data Center Solutions-Slysium Data Center-AUH-ABB Furse.pdfdjiceramil

362 Alec Data Center Solutions-Slysium Data Center-AUH-Adaptaflex.pdfdjiceramil

Rigor, ethics, wellbeing and resilience in the ICT doctoral journeyYannis

chemistry investigatory project for class 12Susis10

Water demand - Types , variations and WDSdhanashree78

社内勉強会資料_Chain of Thought .NABLAS株式会社

SEW make Brake BE05 – BE30 Brake – Repair Kitprojectultramechanix

TEA2016AAT 160 W TV application design examplessuser1be9ce

operationg systemsdocumentmemorymanagementSNIGDHAAPPANABHOTLA

362 Alec Data Center Solutions-Slysium Data Center-AUH-Glands & Lugs, Simplex...djiceramil

IntroSlides-June-GDG-Cloud-Munich community [email protected]Luiz Carneiro

A Comprehensive Investigation into the Accuracy of Soft Computing Tools for D...Journal of Soft Computing in Civil Engineering

grade 9 science q1 quiz.pptx science quiznorfapangolima

22PCOAM16 _ML_Unit 3 Notes & Question bankGuru Nanak Technical Institutions

Selection sort algorithm presentation, selection sort example using power point

2. #Presentation submitted to: Sohrab Hossain, Assistant professor of CSE FSET,USTC #Presentation submitted by: Md Abdul Kuddus Department of CSE ID:15010102 Batch:25th

3. #Presentation Name: Write a program to sort the element of an array using selection sort. #What is selection sort??  Repeatedly searches for the largest value in a section of the data  Moves that value into its correct position in a sorted section of the list  Uses the Find Largest algorithm

4. #Example: Given array: 34 8 64 51 32 21 sorted comparison item unsorted comparison time 0 1 2 3 4 5

5. *pass 1: compare 1st position with minimum item After pass1 *pass2: compare 2nd position with next minimum item After pass2 34 8 64 51 21 8 34 64 51 218 34 64 51 21 8 21 64 51 34

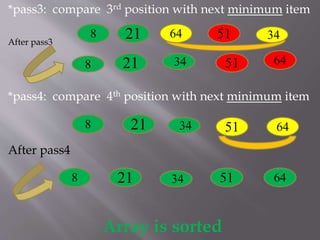
6. *pass3: compare 3rd position with next minimum item After pass3 *pass4: compare 4th position with next minimum item After pass4 Array is sorted 8 21 64 51 34 8 21 34 51 64 8 21 34 51 64 8 21 34 51 64

7. *Algorithm: Algorithm SELECTION(A,N) Step1 : Repeat steps 2 and 3 for k=1,2,….N-1; Step2 : Call MIN(A,K,N,LOC). Step3: [Interchange A[k] and A[LOC].] Set TEMP:=A[k], A[k]:=A[LOC] and A[LOC]:=TEMP. [End of step 1 loop] Step4:Exit.

8. #source code: #include <stdio.h> int *selectionSort(int A[],int n) { int j ,k ,temp; for (k= 0; k < n; k++) { for(j = k+1; j < n; j++) { if(A[k] > A[j]) { temp = A[k]; A[k] = A[j]; A[j] = temp; } } } return A; }

9. int main() { int A[1000],k,n; printf("Enter the number of element you want to Sort : "); scanf("%d",&n); printf("Enter Elements in the list : "); for(k = 0; k < n; k++) { scanf("%d",&A[k]); } int *sortArray = selectionSort(A,n); printf("Sorted list : "); for(k = 0; k < n; k++ ) { printf("%dt",sortArray[k]); } }

10. #Time efficiency  Comparisons: n(n-1)/2  Exchanges: n (swapping largest into place)  Overall: (n2), best and worst cases #Space efficiency  Space for the input sequence, plus a constant number of local variables

Selection sort algorithm presentation, selection sort example using power point

Recommended

More Related Content

What's hot (20)

Similar to Selection sort algorithm presentation, selection sort example using power point (20)

Recently uploaded (20)

Selection sort algorithm presentation, selection sort example using power point