slides-linear-programming-introduction.pdf

Linear Programming: Introduction
Frédéric Giroire
F. Giroire LP - Introduction 1/28

Course Schedule
• Session 1: Introduction to optimization.
Modelling and Solving simple problems.
Modelling combinatorial problems.
• Session 2: Duality or Assessing the quality of a solution.
• Session 3: Solving problems in practice or using solvers (Glpk or
Cplex).

Motivation
Why linear programming is a very important topic?
• A lot of problems can be formulated as linear programmes, and
• There exist efficient methods to solve them
• or at least give good approximations.
• Solve difficult problems: e.g. original example given by the
inventor of the theory, Dantzig. Best assignment of 70 people to
70 tasks.
→ Magic algorithmic box.

What is a linear programme?
• Optimization problem consisting in
• maximizing (or minimizing) a linear objective function
• of n decision variables
• subject to a set of constraints expressed by linear equations or
inequalities.
• Originally, military context: "programme"="resource planning".
Now "programme"="problem"
• Terminology due to George B. Dantzig, inventor of the Simplex
Algorithm (1947)

Terminology
max 350x1 +300x2
subject to
x1 +x2 ≤ 200
9x1 +6x2 ≤ 1566
12x1 +16x2 ≤ 2880
x1,x2 ≥ 0
x1,x2 : Decision variables
Objective function
Constraints

Terminology
max 350x1 +300x2
subject to
x1 +x2 ≤ 200
9x1 +6x2 ≤ 1566
12x1 +16x2 ≤ 2880
x1,x2 ≥ 0
x1,x2 : Decision variables
Objective function
Constraints
In linear programme: objective function + constraints are all linear
Typically (not always): variables are non-negative
If variables are integer: system called Integer Programme (IP)

Terminology
Linear programmes can be written under the standard form:
Maximize ∑n
j=1 cj xj
Subject to: ∑n
j=1 aij xj ≤ bi for all 1 ≤ i ≤ m
xj ≥ 0 for all 1 ≤ j ≤ n.
(1)
• the problem is a maximization;
• all constraints are inequalities (and not equations);
• all variables are non-negative.

Example 1: a resource allocation problem
A company produces copper cable of 5 and 10 mm of diameter on a
single production line with the following constraints:
• The available copper allows to produces 21000 meters of cable of
5 mm diameter per week.
• A meter of 10 mm diameter copper consumes 4 times more
copper than a meter of 5 mm diameter copper.
Due to demand, the weekly production of 5 mm cable is limited to
15000 meters and the production of 10 mm cable should not exceed
40% of the total production. Cable are respectively sold 50 and 200
euros the meter.
What should the company produce in order to maximize its weekly
revenue?

Define two decision variables:
• x1: the number of thousands of meters of 5 mm cables produced
every week
• x2: the number of thousands meters of 10 mm cables produced
every week
The revenue associated to a production (x1,x2) is
z = 50x1 +200x2.
The capacity of production cannot be exceeded
x1 +4x2 ≤ 21.

The demand constraints have to be satisfied
x2 ≤
4
10
(x1 +x2)
x1 ≤ 15
Negative quantities cannot be produced
x1 ≥ 0,x2 ≥ 0.

The model: To maximize the sell revenue, determine the solutions of
the following linear programme x1 and x2:
max z = 50x1 +20x2
subject to
x1 +4x2 ≤ 21
−4x1 +6x2 ≤ 0
x1 ≤ 15
x1,x2 ≥ 0

Example 2: Scheduling
• m = 3 machines
• n = 8 tasks
• Each task lasts x units of
time
Objective: affect the tasks to the machines in order to minimize the
duration
• Here, the 8 tasks are finished after 7 units of times on 3
machines.

• m = 3 machines
• n = 8 tasks
time
Objective: affect the tasks to the machines in order to minimize the
duration
• Now, the 8 tasks are accomplished after 6.5 units of time: OPT?
• mn
possibilities! (Here 38
= 6561)

• m = 3 machines
• n = 8 tasks
time
Solution: LP model.
min t
subject to
∑1≤i≤n ti x
j
i ≤ t (∀j,1 ≤ j ≤ m)
∑1≤j≤m x
j
i = 1 (∀i,1 ≤ i ≤ n)
with x
j
i = 1 if task i is affected to machine j.

Solving Difficult Problems
• Difficulty: Large number of solutions.
• Choose the best solution among 2n
or n! possibilities: all solutions
cannot be enumerated.
• Complexity of studied problems: often NP-complete.
• Solving methods:
• Optimal solutions:
• Graphical method (2 variables only).
• Simplex method.
• Approximations:
• Theory of duality (assert the quality of a solution).
• Approximation algorithms.

Graphical Method
• The constraints of a linear programme define a zone of solutions.
• The best point of the zone corresponds to the optimal solution.
• For problem with 2 variables, easy to draw the zone of solutions
and to find the optimal solution graphically.

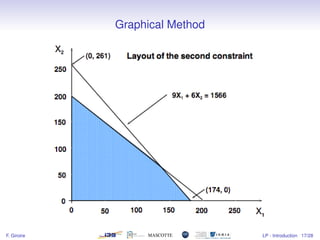
Graphical Method
Example:
max 350x1 +300x2
subject to
x1 +x2 ≤ 200
9x1 +6x2 ≤ 1566
12x1 +16x2 ≤ 2880
x1,x2 ≥ 0

Graphical Method

Computation of the optimal solution
The optimal solution is at the intersection of the constraints:
x1 +x2 = 200 (2)
9x1 +6x2 = 1566 (3)
We get:
x1 = 122
x2 = 78
Objective = 66100.

Optimal Solutions: Different Cases

Three different possible cases:
• a single optimal solution,
• an infinite number of optimal solutions, or
• no optimal solutions.

Three different possible cases:
• a single optimal solution,
• an infinite number of optimal solutions, or
• no optimal solutions.
If an optimal solution exists, there is always a corner point optimal
solution!

Solving Linear Programmes

• The constraints of an LP give rise to a geometrical shape: a
polyhedron.
• If we can determine all the corner points of the polyhedron, then
we calculate the objective function at these points and take the
best one as our optimal solution.
• The Simplex Method intelligently moves from corner to corner
until it can prove that it has found the optimal solution.

• Geometric method impossible in higher dimensions
• Algebraical methods:
• Simplex method (George B. Dantzig 1949): skim through the
feasible solution polytope.
Similar to a "Gaussian elimination".
Very good in practice, but can take an exponential time.
• Polynomial methods exist:
• Leonid Khachiyan 1979: ellipsoid method. But more theoretical
than practical.
• Narendra Karmarkar 1984: a new interior method. Can be used in
practice.

But Integer Programming (IP) is different!
• Feasible region: a set of
discrete points.
• Corner point solution not
assured.
• No "efficient" way to solve
an IP.
• Solving it as an LP provides
a relaxation and a bound on
the solution.

Summary: To be remembered
• What is a linear programme.
• The graphical method of resolution.
• Linear programs can be solved efficiently (polynomial).
• Integer programs are a lot harder (in general no polynomial
algorithms).
In this case, we look for approximate solutions.

slides-linear-programming-introduction.pdf

More Related Content

Similar to slides-linear-programming-introduction.pdf (20)

More from SantiagoGarridoBulln (16)

Recently uploaded (20)

slides-linear-programming-introduction.pdf