Structure tensor-based Gaussian kernel edge-adaptive depth map refinement with triangular point view in images

IAES International Journal of Artificial Intelligence (IJ-AI)
Vol. 13, No. 2, June 2024, pp. 1945~1953
ISSN: 2252-8938, DOI: 10.11591/ijai.v13.i2.pp1945-1953  1945
Journal homepage: http://ijai.iaescore.com
Structure tensor-based Gaussian kernel edge-adaptive depth
map refinement with triangular point view in images
H. Shalma1
, P. Selvaraj2
1
Department of Computing Technologies, School of computing, SRM Institute of Science and Technology, Tamil Nadu, India
2
Department of Computing Technologies, Faculty of Engineering and Technology, SRM Institute of Science and Technology, Tamil
Nadu, India
Article Info ABSTRACT
Article history:
Received May 6, 2023
Revised Oct 27, 2023
Accepted Dec 14, 2023
Image reconstruction is the process of restoring the image resolution. In 3D
image reconstruction, the objects in different viewpoints are processed with
the triangular point view (TPV) method to estimate object geometry
structure for 3D model. This work proposes a depth refinement methodology
in preserving the geometric structure of objects using the structure tensor
method with a Gaussian filter by transforming a series of 2D input images
into a 3D model. The computation of depth map errors can be found by
comparing the masked area/patch with the distribution of the original
image's greyscale levels using the error pixel-based patch extraction
algorithm. The presence of errors in the depth estimation could seriously
deteriorate the quality of the 3D effect. The depth maps were iteratively
refined based on histogram bins number to improve the accuracy of initial
depth maps reconstructed from rigid objects. The existing datasets such as
the dataset tanks and unit (DTU) and Middlebury datasets, were used to
build the model out of the object scene structure. The results of this work
have demonstrated that the proposed patch analysis outperformed the
existing state of the art models depth refinement methods in terms of
accuracy.
Keywords:
Correspondence point
Image matching
Multi-view images
Object recognition
Reconstruction
Triangulation
This is an open access article under the CC BY-SA license.
Corresponding Author:
P. Selvaraj
Department of Computing Technologies, Faculty of Engineering and Technology
SRM Institute of Science and Technology
Kattankulathur-603203, Chengalpattu District, Tamil Nadu, India
Email: selvarap@srmist.edu.in
1. INTRODUCTION
Stereoscopy plays a vital role in computer vision-based systems. Stereo vision involves the process
of estimating the 3D models of the scene. Stereo vision employs techniques like triangulation. The process of
3D reconstruction applies triangulation to generate the 3D models from a set of images. The projection of a
3D scene onto a 2D plane leads to some depth loss, as the corresponding image points are constrained to the
line of sight from a human's viewpoint. From a single view, the corresponding image points with the line of
sight are difficult to match for 3D projection. This problem can be tackled by using multiple images where
the correspondence image point can be found by the intersection of two projection rays from the object. This
process refers to triangulation, followed to identify the structure or pose of the particular object in the image
and the camera calibration.
In the triangulation process, the convolutional neural network (CNN) with multi-view stereo (MVS)
[1] based stereo matching approach was predominantly applied. Multiple 2D images can be converted into
3D models by exploiting the extrinsic and intrinsic camera parameters. Chang and Ho [2] proposed the depth

 ISSN: 2252-8938
Int J Artif Intell, Vol. 13, No. 2, June 2024: 1945-1953
1946
determination of contours from the image point coordination between pairs of images. Moreover, they have
mentioned that the correspondence problem of finding the matched images can be triangulated in 3D space.
The measure of disparity would be used to identify the structure or pose of a particular object. The
measure of disparity can be used to predict the object distance from the camera viewpoint. The item closest
to the camera is the one closest in depth. Khalil et al. [3] proposed a disparity measure based depth map
estimation. The value of the left and right pictures was used to calculate the depth map for the stereo images
at the correspondence point pixel. They have augmented the depth map depending on the structural
magnitude of the 3D model. The lesser the disparity value, the greater the object's depth. Owing to this fact,
the generated adaptive object structure has produced convincing visual quality.
The state-of-the-art models have shown better precision in depth estimation and refinement. The
stereo matching and MVS vision techniques needs to be exploited to recognize objects in patches over the
images. The following, section 2 describes the related works. The methods to calculate the camera
parameters are discussed in section 3. The point-matching algorithm for determining the defect using the
pixel-wise calculation for both the left and right images is discussed in section 4. Finally, section 5 concludes
the work.
2. RELATED WORK
This section discusses the various approaches to handle image reconstruction with stereo matching
and multi-view stereo network (MVSNet) using similarity metrices. Scharstein and Szeliski [4] reviewed that
the stereo unification/match algorithm usually consists of steps, such as matching of cost calculation,
matching of aggregation cost, disparity value calculation, and disparity enhancement. Aggregation of match
costs with the neighborhood pixel points for local or specific methods [5]–[7] would choose the optimal
disparity based on the winner-take-all strategy. Global or generic methods proposed in [8], [9] depicted that
the energy function could be used to minimize the optimal disparity.
According to Huang et al. [10], a semi-global matching algorithm was designed for the
approximation of optimizing global methods with dynamic programming. Kendall et al. [11], the regression
of disparity maps obtained from the stereo pair matching and learning of geometric structure by the deep
stereo network was done with MVS. Zhang et al. [12] the contextual information from the cost volume was
learned using 3D convolutions using end-to-end architecture. MVSNet [13] and pyramid stereo matching
network (PSMNet) [14] represented the underlying/base networks for demonstrating the cascade cost volume
applications in stereo matching tasks. In the context of CNN based networks, the similarity measure of small
patch images was used in stereo matching methods with softmax argmin operation to provide better matching
results for 3D cost volume in stereo [15]. The 3D cost volume can boost the overall performance. However,
they are less prone to down-sampled cost volumes, and to generate high-resolution disparity images, they
rely on interpolation [16] operations. The most availed method in 3D is the cost volume, first introduced by
the global context network (GCNet) [8] for stereo vision, which uses the regression technique for finding the
best match results with the identification of the intensity range of masked and unmasked regions using
softargmin operation.
The cascade cost volume proposed by Gu et al. [17] demonstrated a method for MVS stereo and
stereo matching and compared their results with the learning-based approaches for accuracy and less memory
usage. This method has used homography warping with CNN for hypothesis depth estimation using feature
pyramids utilizing the low-level features with the downsampling technique. In the areas of ill-posed
occurrences, which are mainly caused by repeated patterns, occluded regions, texture-less regions, and
reflexive planes, the cost of estimating the pixel-wise is generally ambiguous. To overcome this issue, cost
volume-based 3D CNN at multiple scales was used to aggregate the contextual information of the images.
This approach has resulted with regularized noise-contamination with high cost.
MVS has higher accuracy in comparison with stereo matching and structure from motion [18]. The
MVS technique, based on cost volume, estimates the relationship between the surface and the voxel. Then,
the 3D point cloud-based method considers 3D points for iterative processing and regression. Depth map
reconstruction finds the depth map and estimation using the reference image and a few source images.
Greene and Roy [19] attenuation aware MVS was designed to improve the matching confidence of volume
using pixel-wise contextual information of extracted features from the local scenes and regularizing the
confidence pair volume with multi-level ray fusion modules.
Recurrent MVSNet [20] was one of the methods used in the MVSNet for object recognition using
recurrent neural networks, which aids in reducing the computational cost by regularizing the 2D cost maps
using gated recurrent unit (GRU) following the depth direction for better prediction. Structural orientation is
essential to elevate the image quality. The enhancement of structural magnitude and orientation also plays a
vital role in the field of 3D imaging application. The geometric structure of the objects could be easily

Int J Artif Intell ISSN: 2252-8938 
Structure tensor-based Gaussian kernel edge-adaptive depth map refinement with … (H. Shalma)
1947
deteriorated with the presence of noises/blurriness and occlusions in the image. So the edge adaptive
mechanisms of metrics such as structural similarity index measure (SSIM), which is superior to mean
squared error, signal to noise ratio, peak signal noise ratio are failed to concentrate on the textured regions
[21]. The image quality prediction in accumulated error areas reveals less structural information for building
a 3D model. The drawback of the structure tensor-based edge adaptive method was analyzed and the gap in
studies were identified. In the proposed approach the structure tensor with Gaussian kernel was applied in
attaining the geometric structure information. The proposed approach is expected to overcome the drawbacks
of the coarse depth maps obtained from traditional methods with increased resolution.
3. PROPOSED METHODOLOGY
Stereo network is the process of creating 3D images from a given set of 2D images taken in multiple
sets or 2 views concerning the camera parameters. The stereo camera positions are similar to human eye
vision in determining objects with the left and right eye simultaneously. The input images from the stereo
vision were preprocessed so as to remove the barrel and tangential distortion. The projection matching with
the image rectification was done after confirming that the images were paired with their respective plane
coordinates. Then, the measures of pixel shifts were used to calculate the disparity map. The Algorithm 1 for
the triangulation point view with stereoNet-based disparity calculation is discussed. The K-nearest neighbor
(KNN) based distance metric was used to determine the distance between the nearby pixels for generating
depth maps based on the camera parameters.
Algorithm 1: Triangulation point view in MVS
Input: Set of images with labeled data
image orientations and resolutions
depth map construction, d is the disparity value
output: depth map enhancement
depth map estimation
while depth map unification do
if d is similar to K-neighboring views, then
if pixel label = class of interest, then
keep d;
project point in X 3D;
else
discard;
end
else
discard;
end
end
3.1. Network architecture for triangulation in stereo networks
Triangulation point view is the method for determining images in a triangle viewpoint for robustly
identifying the scene's structure. The convolutional neural net structure extracts the features of the input
images, and the correspondence matching describes those features among the image pixel-wise for both the
left and right stereo images in a triangulation convergence for understanding the scene structure. Multi-view
triangulation methods [22] suffer from high computational costs. So robust triangulation was proposed to
tackle this problem. The geometric verification was done to find the image matching, and the mismatch will
lead to an adjustment in the rectification of the object geometry structure for coordinating the camera
calibration using the structure tensor method [23].
The pixel-wise matching in both the left and right images is shown in Figure 1(a) with the triangular
point view (TPV) for matching the image coordinate concerning the world coordinate system. The pixel a in
the left image is considered to find the similarity between the pixel from the right image a' that is if the pixel
values a and a' are similar or not is seen by the pixel matching algorithm [24], which is discussed. Figure 1(b)
describes the point projection in a MVSNet with a triangulation point view for the predictions from coarse to
fine-tuning parameters through CNN and the point flow module. The point flow is one of the methods used
to determine the projection of point flows from the camera parameters for obtaining the point cloud as the
data representation. The TPV method was used to refine coarse depth prediction to achieve a better
refinement strategy using 3D CNN regression.

 ISSN: 2252-8938
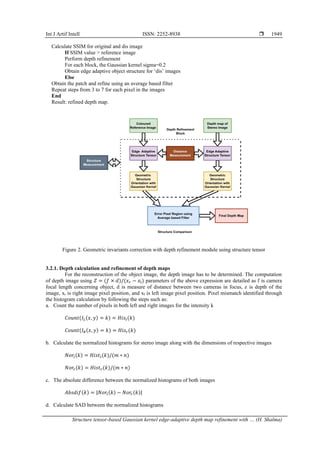
1948
(a)
(b)
Figure 1. Stereo image pair patch selection, (a) for pixel-wise matching in stereo-based images and (b)
projection of return on investmen (ROI) in triangulation viewpoint
3.2. Depth refinement methodology
To triangulate the scene, the correspondence search in the given set of images was performed with
the overlapped regions and the projections of the same points were found. The features were detected as
invariant to any geometric changes; feature matching was also done to provide the output as the
correspondence feature pair for linearity. This technique suits well for the smaller sets of images, which are
less error-prone than the more extensive set of images. Figure 2 describes the structure comparison before
and after the refinement of depth maps.
The point matching finds the difference of given images by the following sum of absolute difference
(SAD) metric or SSIM; usually, in the 3D reconstruction model, the representation of multiple 2D images in
the form as I = {𝐼1 , 𝐼2, . . . . . . . . . 𝐼𝑛} and the corresponding matching of the pixels of the input image was done
using the stereo matching technique with the TPV-based images from the camera viewpoint are denoted as
𝐼𝑖 = 𝑚𝑎𝑡𝑐ℎ(𝑥1, 𝑡1) where the x1 represents the pixel value of the input image into consideration. Moreover,
the t1 is the template pixel or ground truth value for the matching image. The matching of images was done
either by template match or the pixel-wise match (Algorithm 2).
Algorithm 2: For pixel matching and finding deterioration among images
Input: Coarse Depth Map
Output: Refined Depth Map
Read the input RGB stereo image.
Calculate disparity ‘dis’
Set numdisparities=64 and block size=11 based on resolution

1949
Calculate SSIM for original and dis image
If SSIM value > reference image
Perform depth refinement
For each block, the Gaussian kernel sigma=0.2
Obtain edge adaptive object structure for ‘dis’ images
Else
Obtain the patch and refine using an average based filter
Repeat steps from 3 to 7 for each pixel in the images
End
Result: refined depth map.
Figure 2. Geometric invariants correction with depth refinement module using structure tensor
3.2.1. Depth calculation and refinement of depth maps
For the reconstruction of the object image, the depth image has to be determined. The computation
of depth image using 𝑍 = (𝑓 × 𝑑)/(𝑥𝑟 − 𝑥l) parameters of the above expression are detailed as f is camera
focal length concerning object, d is measure of distance between two cameras in focus, z is depth of the
image, xr is right image pixel position, and xl is left image pixel position. Pixel mismatch identified through
the histogram calculation by following the steps such as:
a. Count the number of pixels in both left and right images for the intensity k
𝐶𝑜𝑢𝑛𝑡(𝐼𝐿(𝑥, 𝑦) = 𝑘) = 𝐻𝑖𝑠𝑙(𝑘)
𝐶𝑜𝑢𝑛𝑡(𝐼𝑅(𝑥, 𝑦) = 𝑘) = 𝐻𝑖𝑠𝑟(𝑘)
b. Calculate the normalized histograms for stereo image along with the dimensions of respective images
𝑁𝑜𝑟𝑙(𝑘) = 𝐻𝑖𝑠𝑡𝑙(𝑘)/(𝑚 ∗ 𝑛)
𝑁𝑜𝑟𝑟(𝑘) = 𝐻𝑖𝑠𝑡𝑟(𝑘)/(𝑚 ∗ 𝑛)
c. The absolute difference between the normalized histograms of both images
𝐴𝑏𝑠𝑑𝑖𝑓(𝑘) = |𝑁𝑜𝑟𝑙(𝑘) − 𝑁𝑜𝑟𝑟(𝑘)|
d. Calculate SAD between the normalized histograms

 ISSN: 2252-8938
1950
𝑆𝐴𝐷𝑛𝑜𝑟𝑚ℎ𝑖𝑠𝑡 = 𝑠𝑢𝑚(𝐴𝑏𝑠𝑑𝑖𝑓(𝑘))
𝑤ℎ𝑒𝑟𝑒 𝑘 = 0,1,2, … . 𝐿 − 1 where L is the maximum intensity level (usually 256 for 8-bit images).
4. EXPERIMENTAL RESULTS
In the proposed work, the DTU and the Middlebury datasets were used [25] for evaluating the
triangulation and pyramidal structure in this MVSNet. These datasets contain images taken under different
lighting conditions covering 124 scenes examined in 7 different lighting conditions at 49 or 64 view
directions. Then, the real-world scene correspondence with small-depth scale images taken from the Tanks
and Temple dataset [26], contains realistic scenes with small depth ranges. These training sets were evaluated
with TPV method and compared with several MVSNet structures such as FastMVS (extracts features before
projecting onto plane), DeepMVS and PyramidMVS.
4.1. Implementation
The accuracy and completeness measures of the DTU datasets were computed for the scenes
exposed under different lighting conditions. The input taken from the DTU dataset was fed into the
prediction pattern of CNN to identify the dissimilarity measure among the different sets of inputs for object
recognition. The training image, taken from the MVS strategy, was analyzed with the state of the models for
comparative results. Figure 3(a) to Figure 3(d) describes the intensity variation result and disparity image for
the provided inputs using the subtraction method and distance measurement of pixel match, respectively. The
input ill-posed images, such as those that underwent different lighting, texture, and occlusions considered for
reconstruction, are done via different model architectures.
Figure 4(a) to Figure 4(d) describes the processing of stereo images by the edge adaptive structure
method in obtaining the fine depth map from the coarse depth map. The depth map was enhanced using
kernel parameter with sigma=0.2. The edge adaptive kernel based on the blocksize was choosen to get a
refined depth map for better visualization quality in a 3D model.
(a) (b) (c) (d)
Figure 3. Stereo imaging correspondence pixel coordination (a) Left Image (b) Right Image, (c) initial depth
map, and (d) disparity map without pixel matching
(a) (b) (c) (d)
Figure 4. Structure preserving smoothness a) disparity map with distance pixel measurement using color, (b)
coarse depth map, (c) edge adaptive kernel-based structure tensor method for predicting geometric structure
of objects visibility in construction of 3D model, and (d) final refined depth maps.

1951
Table 1 describes the similarity measure from the input stereo images with rectification and without
rectification values. The value of SSIM rectified stereo images is nearer to the max value, and the accuracy of
final depth map compared with initial depth maps is higher. Refining depth maps using the structure tensor
method with Gaussian kernel obtains the refined depth map with better accuracy. Table 2 describes the
quantitative measure of TPV with histogram patch matching is compared with the algorithm grab-cut and
Traditional histogram for analyzing the pixel probability distribution range. The ranges are decided based on
the bin selected for various objects in the image. The precision results of the images are evaluated using
metrics such as the mean absolute elevation error and root mean square error (RMSE). The edge adaptive
structure tensor method using TPV in correspondence pixel match achieves higher accuracy than other
models using grab-cut optimization parameters. The lesser mean absolute error value in pixel matching
reduces the complexity of the deteriorate effect in the selective patch.
Table 1. Similarity metric for rectified and unrectified images
Image MAE RMSE SSIM Structure tensor similarity measure
Unrectified stereo images 5864.73 76.5 0.407,0.415 17.014
Rectified stereo images 1292.95 35.9 0.544,0.607 10.448
Table 2. The RMSE and mean elevation error (pixels)
Algorithms Masked region UnMasked region
RMSE Mean absolute elevation error RMSE Mean absolute elevation error
Grab-cut method 0.117 0.326 0.119 0.371
Traditional histogram 0.806 0.114 0.128 0.602
TPV method +histogram patch matching 0.108 0.136 0.052 0.214
4.2. Stereo matching
This section uses the histogram analysis method to describe the datasets used for stereo-matching
images in creating disparity maps for the respective problem. The histogram calculation for the given images
uses the OpenCV histogram method, which takes a positional argument as the input image, channels, mask,
intensity values, and pixel value for every pixel. The mask was chosen based on the user's decision to select
the region on which the algorithm has to work/depend for pixel matching. The class intervals are calculated
based on the data points in the image. Figure 5 shows how the mask is chosen for the particular patch to
identify the occluded or mismatched pixel region. The masked histogram can show the pixel deformity and
aid smoothing using filters. The results shown in Figure 5 are taken from Middlebury dataset.
Figure 5. Image histogram for the mask and unmask region
Mask region suggested using the number of bins in a color histogram to represent the distance
between classes. Histograms of good quality require patches with sufficiently large numbers of sample
pixels. A non-contextual edge detector such as the conventional Canny operator produces strong responses to
texture areas when textures and object sizes are comparable. Object contours may be obscured in the final
product of such an operator. Compare the colors of masked and unmasked patches of images for precision
evaluation with traditional methods. Figure 6 demonstrates how accuracy is achieved with the different
methods in the iterative refinement of depth maps concerning iterations. The depth map is refined to correct
the boundaries and check the misalignment between the red, green, blue (RGB) image and the depth map.

 ISSN: 2252-8938
1952
Figure 6. Number of Iterations for achieving accuracy using different methods
5. CONCLUSION
Hence a novel TPV-based object texture identification was proposed. We have analyzed the
efficiency of the proposed algorithm under different lighting conditions using the SAD method. The
determination of pixel-wise similarity matching was done using the pixel match algorithm for both the left
and right images and they were analysed with the other metrics such as SSIM and mean square error. The
TPV method, along with the camera parameter, serves as the input for pixel matching and the depth maps
were found to process the input image for better perception of the scene. The histogram of images determines
the pixel intensity variations due to occlusion or discontinuities in the disparity map. This identification has
led the system to deal with the problem caused by object occlusion in stereo images. As a future
enhancement utilization of super-pixels in the patch-based method will be tested instead of taking all patches
of an image in a holistic manner.
REFERENCES
[1] E. K. Stathopoulou and F. Remondino, “Multi view stereo with semantic priors,” International Archives of the Photogrammetry,
Remote Sensing and Spatial Information Sciences-ISPRS Archives, pp. 1135-1140, 2020, doi: 10.5194/isprs-archives-XLII-2-
W15-1135-2019.
[2] Y. J. Chang and Y. S. Ho, “Disparity map enhancement in pixel based stereo matching method using distance transform,” Journal
of Visual Communication and Image Representation, vol. 40, pp. 118–127, 2016, doi: 10.1016/j.jvcir.2016.06.017.
[3] S. A.-Khalil, S. A.-Rahman, S. Mutalib, S. I. Kamarudin, and S. S. Kamaruddin, “A review on object detection for autonomous
mobile robot,” IAES International Journal of Artificial Intelligence, vol. 12, no. 3, pp. 1033–1043, 2023, doi:
10.11591/ijai.v12.i3.pp1033-1043.
[4] D. Scharstein and R. Szeliski, “A taxonomy and evaluation of dense two-frame stereo correspondence algorithms,” International
Journal of Computer Vision, vol. 47, no. 1–3, pp. 7–42, 2002, doi: 10.1023/A:1014573219977.
[5] X. Mei, X. Sun, W. Dong, H. Wang, and X. Zhang, “Segment-tree based cost aggregation for stereo matching,” in 2013 IEEE
Conference on Computer Vision and Pattern Recognition, 2013, pp. 313–320, doi: 10.1109/CVPR.2013.47.
[6] Q. Yang, “A non-local cost aggregation method for stereo matching,” in 2012 IEEE Conference on Computer Vision and Pattern
Recognition, 2012, pp. 1402–1409, doi: 10.1109/CVPR.2012.6247827.
[7] K. Zhang, J. Lu, and G. Lafruit, “Cross-based local stereo matching using orthogonal integral images,” IEEE Transactions on
Circuits and Systems for Video Technology, vol. 19, no. 7, pp. 1073–1079, 2009, doi: 10.1109/TCSVT.2009.2020478.
[8] H. Hirschmüller, “Stereo processing by semiglobal matching and mutual information,” IEEE Transactions on Pattern Analysis
and Machine Intelligence, vol. 30, no. 2, pp. 328–341, 2008, doi: 10.1109/TPAMI.2007.1166.
[9] A. Klaus, M. Sormann, and K. Karner, “Segment-based stereo matching using belief propagation and a self-adapting dissimilarity
measure,” in 18th International Conference on Pattern Recognition (ICPR'06), 2006, pp. 15–18, doi: 10.1109/ICPR.2006.1033.
[10] Z. Huang, J. Gu, J. Li, and X. Yu, “A stereo matching algorithm based on the improved PSMNet,” PLoS ONE, vol. 16, no. 8, pp.
1–16, 2021, doi: 10.1371/journal.pone.0251657.
[11] A. Kendall et al., “End-to-end learning of geometry and context for deep stereo regression,” in 2017 IEEE International
Conference on Computer Vision (ICCV), Oct. 2017, pp. 66–75, doi: 10.1109/ICCV.2017.17.
[12] M. Ji, J. Zhang, Q. Dai, and L. Fang, “SurfaceNet+: An End-to-end 3D neural network for very sparse multi-view stereopsis,”
IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 43, no. 11, pp. 4078–4093, 2021, doi:
10.1109/TPAMI.2020.2996798.
[13] J. Yang, J. M. Alvarez, and M. Liu, “Self-supervised learning of depth inference for multi-view stereo,” in 2021 IEEE/CVF
Conference on Computer Vision and Pattern Recognition (CVPR), Jun. 2021, pp. 7522–7530, doi:
10.1109/CVPR46437.2021.00744.
[14] J. R. Chang and Y. S. Chen, “Pyramid stereo matching network,” in 2018 IEEE/CVF Conference on Computer Vision and Pattern
Recognition, 2018, pp. 5410–5418, doi: 10.1109/CVPR.2018.00567.
[15] J. Žbontar and Y. Le Cun, “Computing the stereo matching cost with a convolutional neural network,” in 2015 IEEE Conference
on Computer Vision and Pattern Recognition (CVPR), 2015, pp. 1592–1599, doi: 10.1109/CVPR.2015.7298767.
[16] S. Agarwal, S. Khade, Y. Dandawate, and P. Khandekar, “Three dimensional image reconstruction using interpolation of distance
and image registration,” in IEEE International Conference on Computer Communication and Control, IC4 2015, 2016, pp. 4–8,
doi: 10.1109/IC4.2015.7375709.
[17] X. Gu, Z. Fan, S. Zhu, Z. Dai, F. Tan, and P. Tan, “Cascade cost volume for high-resolution multi-view stereo and stereo
0
0.2
0.4
0.6
0.8
1
1 2 3 4 5
Deep MVS
Fast MVS
TPV+StructureTensorwithpyramidMVS
Pyramid MVS

1953
matching,” in 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2020, pp. 2492–2501, doi:
10.1109/CVPR42600.2020.00257.
[18] J. L. Schonberger and J. M. Frahm, “Structure-from-motion revisited,” in 2016 IEEE Conference on Computer Vision and Pattern
Recognition (CVPR), 2016, pp. 4104–4113, doi: 10.1109/CVPR.2016.445.
[19] W. N. Greene and N. Roy, “MultiViewStereoNet: fast multi-view stereo depth estimation using incremental viewpoint-
compensated feature extraction,” in 2021 IEEE International Conference on Robotics and Automation (ICRA), 2021, pp. 9242–
9248, doi: 10.1109/icra48506.2021.9562096.
[20] Y. Yao, Z. Luo, S. Li, T. Shen, T. Fang, and L. Quan, “Recurrent MVSNet for high-resolution multi-view stereo depth inference,”
in 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Jun. 2019, pp. 5520–5529, doi:
10.1109/CVPR.2019.00567.
[21] X. Fei, L. Xiao, Y. Sun, and Z. Wei, “Perceptual image quality assessment based on structural similarity and visual masking,”
Signal Processing: Image Communication, vol. 27, no. 7, pp. 772–783, 2012, doi: 10.1016/j.image.2012.04.005.
[22] C. Aholt, S. Agarwal, and R. Thomas, “A QCQP approach to triangulation,” in Computer Vision–ECCV 2012), Berlin,
Heidelberg: Springer, 2012, pp. 654–667, doi: 10.1007/978-3-642-33718-5_47.
[23] N. Ma, P. F. Sun, Y. B. Men, C. G. Men, and X. Li, “A Subpixel matching method for stereovision of narrow baseline remotely
sensed imagery,” Mathematical Problems in Engineering, vol. 2017, pp. 1-15, 2017, doi: 10.1155/2017/7901692.
[24] R. Chen, S. Han, J. Xu, and H. Su, “Visibility-aware point-based multi-view stereo network,” IEEE Transactions on Pattern
Analysis and Machine Intelligence, vol. 43, no. 10, pp. 3695–3708, 2021, doi: 10.1109/TPAMI.2020.2988729.
[25] H. Aanæs, R. R. Jensen, G. Vogiatzis, E. Tola, and A. B. Dahl, “Large-scale data for multiple-view stereopsis,” International
Journal of Computer Vision, vol. 120, no. 2, pp. 153–168, 2016, doi: 10.1007/s11263-016-0902-9.
[26] R. Chen, S. Han, J. Xu, and H. Su, “Point-based multi-view stereo network,” in 2019 IEEE/CVF International Conference on
Computer Vision (ICCV), Oct. 2019, pp. 1538–1547, doi: 10.1109/ICCV.2019.00162.
BIOGRAPHIES OF AUTHORS
H. Shalma holds a Bachelor of Engineering (B.E) in Computer Science and
Engineering in 2012, Master of Engineering (M.E) in Computer Science and Engineering in
2014, and currently Pursuing Ph.D. in Computer Science and Engineering at SRM University,
Chennai. She has the teaching experience of 4 years in Computer Science and Engineering.
Her research areas of interest include artificial intelligent, deep learning, computer vision,
pattern recognition, and photogrammetry. She has published few research papers in
international journal and conferences. She can be contacted at email: Sh3369@srmist.edu.in.
P. Selvaraj is currently working as an associate professor in the Department of
Computing Technologies, SRM Institute of Science and Technology, Kattankulathur,
Chennai, Tamil Nadu, India. He has been working in SRMIST for the past 18 years. He
published 37 indexed journals in the fields of IoT, bigdata, computer vision, and intelligent
networks. He is constantly involved in research related to artificial intelligence with IoT. He is
currently guiding 5 research scholars. He can be contacted at email: selvarap@srmist.edu.in.

Structure tensor-based Gaussian kernel edge-adaptive depth map refinement with triangular point view in images

More Related Content

Similar to Structure tensor-based Gaussian kernel edge-adaptive depth map refinement with triangular point view in images (20)

More from IAESIJAI (20)

Recently uploaded (20)

Structure tensor-based Gaussian kernel edge-adaptive depth map refinement with triangular point view in images