(chapter 9) A Concise and Practical Introduction to Programming Algorithms in Java
- 1. 1 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Frank NIELSEN [email protected] A Concise and Practical Introduction to Programming Algorithms in Java Chapter 9: Combinatorial optimization algorithms
- 2. 2 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen A few algorithms and paradigms: - I/ Exhaustive search - II/ Greedy algorithm (set cover problems) - III/ Dynamic programming (knapsack) Agenda +...Merging two lists...
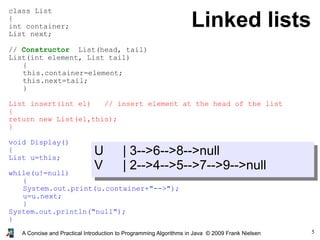
- 3. 3 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Linked lists public class List { int container; List next; // a reference to a cell of a list // Constructor List(head, tail) // Build a cell so that // the reference to the next cell is the tail List(int element, List tail) { this.container=element; this.next=tail; } } next=null
- 4. 4 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Merging ordered linked lists ● Two linked lists u and v of increasing integers ● Build a new linked list in increasing order... ● ...using only cells of u and v (no cell creation, new) U | 3-->6-->8-->null V | 2-->4-->5-->7-->9-->null Merge(U,V) | 2-->3-->4-->5-->6-->7-->8-->9-->null For example:
- 5. 5 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Linked lists class List { int container; List next; // Constructor List(head, tail) List(int element, List tail) { this.container=element; this.next=tail; } List insert(int el) // insert element at the head of the list { return new List(el,this); } void Display() { List u=this; while(u!=null) { System.out.print(u.container+"-->"); u=u.next; } System.out.println("null"); } } U | 3-->6-->8-->null V | 2-->4-->5-->7-->9-->null
- 6. 6 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen class MergeList { // // Merge two ordered lists // static List mergeRec(List u, List v) { if (u==null) return v; if (v==null) return u; if (u.container < v.container) { // Recycle cells/ no new u.next=mergeRec(u.next,v); return u; } else { // Recycle cells/no new v.next=mergeRec(u,v.next); return v; } } public static void main(String [] args) { List u=new List(8,null); u=u.insert(6);u=u.insert(3); u.Display(); List v=new List(9,null); v=v.insert(7);v=v.insert(5); v=v.insert(4);v=v.insert(2); v.Display(); List w=mergeRec(u,v); w.Display(); }
- 7. 7 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen static List sortRec(List u) { int i,l=u.length(), lr; List l1, l2, split, psplit; // references to cells if (l<=1) return u; else { l1=u; psplit=split=u; i=0;lr=l/2; while (i<lr) {i++; psplit=split; split=split.next;} l2=split; // terminates with a null psplit.next=null; return mergeRec( sortRec(l1), sortRec(l2) ); } } Sort in O(n log n) time: ● Split list in two halves ● Recursively apply sorting ● Merge ordered lists
- 8. 8 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen public static void main(String [] args) { List u=new List(3,null); u=u.insert(2); u=u.insert(9); u=u.insert(6);u=u.insert(1); u=u.insert(15);u=u.insert(17); u=u.insert(23);u=u.insert(21); u=u.insert(19);u=u.insert(20); u.Display(); List sortu=sortRec(u); System.out.println("Sorted linked list:"); sortu.Display(); } 20-->19-->21-->23-->17-->15-->1-->6-->9-->2-->3-->null Sorted linked list: 1-->2-->3-->6-->9-->15-->17-->19-->20-->21-->23-->null
- 9. 9 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Exhaustive search (Brute force search) The Eight Queens puzzle: ● 92 distinct solutions ● 12 non-naive distinct solutions (rotation/symmetry) ● Good exercise for designing algorithms ● Generalize to n-queens Max Bezzel (1848, chess player) Find safe positions of 8 queens on a 8x8 chessboard
- 10. 10 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Exhaustive search & Backtracking Brute force (naive) algorithm: Check all 64x63x...x57/8! = 283,274,583,552 ?! solutions... Easy to check that a configuration is not safe (check horizontal/vertical/diagonal lines) → Two queens cannot be on the same line... Therefore, incrementally place queen i (0...7) on the i-th row, on the first free column If there is no more free columns left, then backtrack... backtrack...
- 11. 11 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Exhaustive search & Backtracking Incrementally place queen i (0...7) on the first free column If there is no more free columns left, then backtrack: backtrack: Consider the previous queen position and increment its column position, etc., etc., etc. ... until we find a solution (=reach a successful location for queen indexed 7) queen: 1D Array that specifies the column position Queen i is located at position (i,queen[i]) (with i ranging from 0 to 7) search: Static function that returns a/all solution(s).
- 12. 12 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen // Are queen (i1,j1) and queen (i2,j2) safe ? static boolean WrongPos(int i1, int j1, int i2, int j2) { // same row?, same col?, same diag? return (i1==i2 || j1==j2 || Math.abs(i1-i2) == Math.abs(j1-j2)); } // Place safely queen i at column j? static boolean FreeMove(int i, int j) { boolean result=true; for(int k=0;k<i;k++) result=result&&!WrongPos(i,j,k,queen[k]); return result; } Check for the queens placed so far on the chessboard Static functions to check for collisions
- 13. 13 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen static boolean search(int row) { boolean result=false; if (row==n) {// Terminal case DisplayChessboard(); nbsol++; } else {// Exhaustive search int j=0; while(!result && j<n) { if (FreeMove(row,j)) { queen[row]=j; result=search(row+1); // RECURSION/BACKTRACK } j++; // explore all columns } } return result; } Increment the number of found solutions (static class variable)
- 14. 14 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen public static void main(String [] arguments) { nbsol=0; search(0); // Call exhaustive search procedure System.out.println("Total number of solutions:"+nbsol); } static final int n=8; static int [] queen=new int[n]; static int nbsol; static void DisplayChessboard() { int i,j; System.out.println(""); for(i=0;i<n;i++) { for(j=0;j<n;j++) { if (queen[i]!=j) System.out.print("0"); else System.out.print("1"); } System.out.println(""); } }
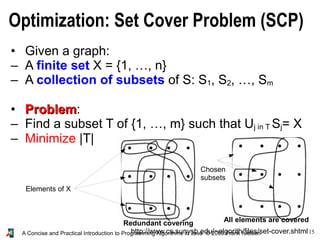
- 15. 15 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Optimization: Set Cover Problem (SCP) http://www.cs.sunysb.edu/~algorith/files/set-cover.shtml • Given a graph: – A finite set X = {1, …, n} – A collection of subsets of S: S1, S2, …, Sm • Problem Problem: – Find a subset T of {1, …, m} such that Uj in T Sj= X – Minimize |T| Elements of X Chosen subsets All elements are covered Redundant covering
- 16. 16 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Applications of set cover problems ● Choose base stations for quality of service (cell phone network, etc) ● Discretize terrain using a regular grid (set X) ● Each position of antenna -> subset of covered grid areas (S) ● Minimize the number of chosen antennas (X) Wave propagation patterns of a single antenna Mountains City
- 17. 17 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen • Given a graph: – A finite set X = {1, …, n} (=regular grid elements) – A collection of subsets of S (=antenna patterns) S1, S2, …, Sm • Problem Problem: – Find a subset T of {1, …, m} (=subset of antennas) such that Uj in T Sj= X – Minimize |T| Covered once Covered twice Covered thrice
- 18. 18 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen GREEDY-SET-COVER(X,S) 1 M X // all elements must be covered ← 2 C Ø // chosen subsets ← 3 while M ≠ Ø do 4 select an Q Є S that maximizes |Q ח M| 5 M M – Q ← 6 C C U {Q} ← 7 return C A greedy algorithm (algorithme glouton) Set Cover solution Input Output
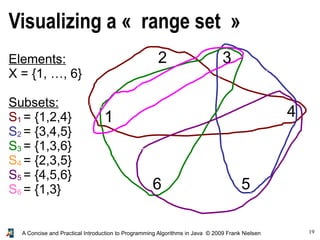
- 19. 19 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Elements: X = {1, …, 6} Subsets: S1 = {1,2,4} S2 = {3,4,5} S3 = {1,3,6} S4 = {2,3,5} S5 = {4,5,6} S6 = {1,3} 1 3 6 5 4 2 Visualizing a « range set »
- 20. 20 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Data-structure for the set cover problem Incidence matrix: boolean matrix X = {1, …, 6} S1 = {1,2,4} S2 = {3,4,5} S3 = {1,3,6} S4 = {2,3,5} S5 = {4,5,6} S6 = {1,3} 1 2 3 4 5 6 1 1 0 1 0 0 S1 0 0 1 1 1 0 S2 1 0 1 0 0 1 S3 0 1 1 0 1 0 S4 0 0 0 1 1 1 S5 1 0 1 0 0 0 S6 N=6 ELEMENTS M=6 SUBSETS
- 21. 21 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen class SetCover { int nbelements; int nbsubsets; boolean [][] incidenceMatrix; //Constructor SetCover(int nn, int mm) { this.nbelements=nn; this.nbsubsets=mm; incidenceMatrix=new boolean[nbsubsets][nbelements]; for(int i=0;i<nbsubsets;i++) for(int j=0;j<nbelements;j++) incidenceMatrix[i][j]=false; } void SetSubsets(int [] [] array) // Set incidence matrix {for(int j=0;j<array.length;j++) {for(int i=0;i<array[j].length;i++) incidenceMatrix[j][array[j][i]]=true; } } }
- 22. 22 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen void Display() { for(int i=0;i<nbsubsets;i++){ for(int j=0;j<nbelements;j++) if (incidenceMatrix[i][j]) System.out.print("1"); else System.out.print("0"); System.out.println(""); } } public static void main(String [] args) { int [][] subsets={{0,1,3},{2,3,4}, {0,2,5},{1,2,4},{3,4,5},{0,2}}; SetCover setcover=new SetCover(6,6); setcover.SetSubsets(subsets); System.out.println("Set cover problem:"); setcover.Display(); }
- 23. 23 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen static boolean [] GreedySCP(SetCover problem) { boolean [] result=new boolean[problem.nbsubsets]; int cover=0; int select; for(int i=0;i<problem.nbsubsets;i++) // initially no subsets result[i]=false; while(cover!=problem.nbelements) { // Choose largest not-yet covered subset select=problem.LargestSubset(); result[select]=true; // Update covered matrix cover+=problem.Cover(select); // Update incidence matrix problem.Update(select); System.out.println("Selected "+select+" Number of covered elements="+cover); problem.Display(); } return result; } Greedy algorithm
- 24. 24 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen // Number of covered element by subset i int Cover(int i) { int nbEl=0; for(int j=0;j<nbelements;j++) if (incidenceMatrix[i][j]) ++nbEl; return nbEl; } // Report the current largest subset int LargestSubset() { int i, nbel, max, select; max=-1;select=-1; for(i=0;i<nbsubsets;i++) { nbel=Cover(i); if (nbel>max) {max=nbel; select=i;} } return select; } Methods of class SetCover
- 25. 25 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Methods of class SetCover // Update the incidence matrix void Update(int sel) { int i,j; for(i=0;i<nbsubsets;i++) { if (i!=sel) //use sel below so don't modify it { for(j=0;j<nbelements;j++) if (incidenceMatrix[sel][j]) incidenceMatrix[i][j]=false; } } // Remove the chosen subset as well for(j=0;j<nbelements;j++) incidenceMatrix[sel][j]=false; }
- 26. 26 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen public static void main(String [] args) { int [] [] subsets ={{0,1,3},{2,3,4}, {0,2,5},{1,2,4}, {3,4,5},{0,2}}; SetCover setcover=new SetCover(6,6); setcover.SetSubsets(subsets); System.out.println("Set cover problem:"); setcover.Display(); boolean [] solution=GreedySCP(setcover); System.out.print("Solution:"); for(int i=0;i<setcover.nbsubsets;i++) if (solution[i]) System.out.print(" "+i); System.out.println(""); } Set cover problem: 110100 001110 101001 011010 000111 101000 Selected 0 Number of covered elements=3 000000 001010 001001 001010 000011 001000 Selected 1 Number of covered elements=5 000000 000000 000001 000000 000001 000000 Selected 2 Number of covered elements=6 000000 000000 000000 000000 000000 000000 Solution: 0 1 2
- 27. 27 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Optimization bounds for greedy algorithm Lower bound: Approximation factor can be as big as Omega(log(n)) Difficult to approximate: cannot beat (1-eps)Opt unless P=NP Upper bound: Approximation factor is at most H(n)<=log(n) 2 sets is optimal solution but greedy chooses 3 sets here CoptT<= Cgreedy <= ApproximationFactor x Copt
- 28. 28 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen int [] [] subsets={{0,1,2,3,4,5,6},{7,8,9,10,11,12,13}, {0,7},{1,2,8,9},{3,4,5,6,10,11,12,13}}; SetCover setcover=new SetCover(14,5); Set cover problem: 11111110000000 00000001111111 10000001000000 01100000110000 00011110001111 Selected 4 Number of covered elements=8 11100000000000 00000001110000 10000001000000 01100000110000 00000000000000 Selected 3 Number of covered elements=12 10000000000000 00000001000000 10000001000000 00000000000000 00000000000000 Selected 2 Number of covered elements=14 00000000000000 00000000000000 00000000000000 00000000000000 00000000000000 Solution: 2 3 4 Etc... Easy to build generic examples where greedy does not behave well with O(log n) approximation ratio
- 29. 29 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Knapsack problem (sac a dos) (First version) Given: ● A set of n Objects O1, ..., On with corresponding weights W1, ..., Wn ● And a bag (knapsack) of capacity W Find: All the ways of choosing objects to fully fill the bag
- 30. 30 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Filling the knapsack Need to enumerate all possibilities: n objects => 2^n choices (2, 4, 8, 16, 32, 64, ...) How to program this? n is a variable (cannot fix the number of nest loops) Need to enumerate all combinations: = Exhaustive search n=4 2^4=16 1 1 1 1 1 1 1 0 1 1 0 1 1 1 0 0 1 0 1 1 1 0 1 0 1 0 0 1 1 0 0 0 0 1 1 1 0 1 1 0 0 1 0 1 0 1 0 0 0 0 1 1 0 0 1 0 0 0 0 1 0 0 0 0
- 31. 31 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Enumerating: A recursive approach static void Display(boolean [] tab) { for(int i=0;i<tab.length;i++) if (tab[i]) System.out.print("1 "); else System.out.print("0 "); System.out.println(""); } static void Enumerate(boolean [] selection, int pos) { if (pos==selection.length-1) Display(selection); else { pos++; selection[pos]=true; Enumerate(selection,pos); selection[pos]=false; Enumerate(selection,pos); } } public static void main(String[] args) { int n=4; int i; boolean [] select=new boolean[n]; for(i=0;i<n;i++) select[i]=false; Enumerate(select,-1); }
- 32. 32 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Fully filling the knapsack static void SolveKnapSack(boolean [] chosen, int goal, int i, int total) { numbercall++; // keep track of total number of calls if ((i>=chosen.length)&&(total!=goal)) return; if (total==goal) { Display(chosen, goal); numbersol++; // total number of solutions } else { chosen[i]=true;// add item first SolveKnapSack(chosen,goal,i+1,total+weight[i]); chosen[i]=false; // and then remove it SolveKnapSack(chosen,goal,i+1,total); } } final static int n=10; // 10 objects static int [] weight={2,3,5,7,9,11,4,13,23,27};
- 33. 33 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen final static int n=10; // 10 objects static int [] weight={2,3,5,7,9,11,4,13,23,27}; public static void main(String [] args) { int totalweight=51; numbersol=0; numbercall=0; System.out.println("Knapsack:"); boolean [] chosen=new boolean[n]; SolveKnapSack(chosen, totalweight, 0, 0); System.out.println("Total number of solutions:"+numbersol); System.out.println(" #calls="+numbercall); } Knapsack: 2+3+5+7+11+23+0=51 2+5+7+9+11+4+13+0=51 2+5+4+13+27+0=51 2+7+11+4+27+0=51 2+9+4+13+23+0=51 2+9+13+27+0=51 3+5+7+9+4+23+0=51 3+5+7+9+27+0=51 3+5+7+13+23+0=51 3+5+9+11+23+0=51 7+4+13+27+0=51 9+11+4+27+0=51 11+4+13+23+0=51 11+13+27+0=51 Total number of solutions:14 #calls=2029
- 34. 34 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Exhaustive search: Branch & bound static void SolveKnapSack(boolean [] chosen, int goal, int i, int total) { numbercall++; if (total>goal) return; // cut if ((i>=chosen.length)&&(total!=goal)) return; if (total==goal) { Display(chosen, goal); numbersol++; } else { chosen[i]=true;// add item first SolveKnapSack(chosen,goal,i+1,total+weight[i]); chosen[i]=false; // and then remove it SolveKnapSack(chosen,goal,i+1,total); } } Stop recursion if we already exceed the weight amount
- 35. 35 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Knapsack: Fundamental optimization problem Given a bag capacity (15 kg), maximize the utility (price) of selected objects (NP-hard problem)
- 36. 36 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Knapsack optimization problem Given weights utility Optimize such that (Maybe there exists several solutions) Maximum weight (capacity of bag)
- 37. 37 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Knapsack: Example = 12 weight utility 8 objects
- 38. 38 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Dynamic programming (Knapsack) Dynamic programming computes a table... ... from which a solution can be retrieved. Requires a relational equation to deduce solutions progressively.
- 39. 39 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Dynamic programming (Knapsack) Let u(i,j) be the maximum utility by taking objects in {1, ...,i} with total weight <=j ● If i=1 then u(i,j)=0 for j<p1 and u(i,j)=A1 for j>=P1 ● If i>1 u(i,j)=max( u(i-1,j) , u(i-1,j-Pi)+Ai ) Take object Oi: ● gain Ai ● but leave room: Pi Do not take object Oi
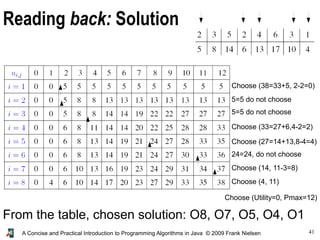
- 40. 40 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen u(i,j)=max( u(i-1,j) , u(i-1,j-Pi)+Ai ) weight utility Pmax= 12 Optimization result: Maximum utility, given Pmax
- 41. 41 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Reading back: Solution Choose (4, 11) Choose (14, 11-3=8) Choose (27=14+13,8-4=4) Choose (33=27+6,4-2=2) Choose (38=33+5, 2-2=0) From the table, chosen solution: O8, O7, O5, O4, O1 Choose (Utility=0, Pmax=12) 24=24, do not choose 5=5 do not choose 5=5 do not choose
- 42. 42 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen static int nbObjects=8; static int [] weight={2,3,5,2,4,6,3,1}; static int [] utility={5,8,14,6,13,17,10,4}; static int weightmax=12; static int [] [] array; static void SolveDP() { int i,j; array=new int[nbObjects][weightmax+1]; // initialize the first row for(j=0;j<=weightmax;j++) if (j<weight[0]) array[0][j]=0; else array[0][j]=utility[0]; // for all other rows for(i=1;i<nbObjects;i++) { for(j=0;j<=weightmax;j++) if (j-weight[i]<0) array[i][j]=array[i-1][j]; else array[i][j]=max( array[i-1][j], array[i-1][j-weight[i]]+utility[i]); } }
- 43. 43 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen static void InterpretArray() { int i,u,w; u=0; w=weightmax; for(i=nbObjects-1;i>=1;i--) { if (array[i][w]!=array[i-1][w]) {System.out.print((i+1)+" "); w=w-weight[i]; u=u+utility[i]; } } if (array[0][w]!=0); {System.out.println("1"); w=w-weight[0]; u=u+utility[0]; } System.out.println("Cross check:"+u+" remaining weight "+w); }
- 44. 44 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen public static void main(String[] args) { System.out.println("Solving knapsack using the dynamic programming paradigm."); SolveDP(); Display(); System.out.println("Reading solution:"); InterpretArray(); }
- 45. 45 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Dynamic programming: binocular stereo matching Benchmark: http://vision.middlebury.edu/~schar/stereo/web/results.php Dynamic Programming
- 46. 46 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Optimization: A brief summary ● Exhaustive search: recursion but O(2^n) complexity ● Can be improved by backtracking (cuts) ● Greedy algorithm: Polynomial O(n^3) ● but yields an approximation ● Dynamic programming yields an exact solution but requires O(weightxobjects) time (weights should not be too bigs)
- 47. 47 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Last but not least: Java applets! Applets are special java programs... ...that can run into your favorite Internet browser You need to: (1) write a web page with <APPLET> </APPLET> tags (2) write and compile the Java applet code (javac) Advantages of applets are: (1) to be accessible worldwide (2) to provide graphics
- 48. 48 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen import java.awt.*; import java.applet.*; class Point2D {double x,y; Point2D() {this.x=300.0*Math.random(); this.y=300.0*Math.random();}} public class AppletINF311 extends Applet { final static int n=100; static Point2D [] set; public void init() { int i; set=new Point2D[n]; for(i=0;i<n;i++) set[i]=new Point2D();} public void paint(Graphics g) {int i; for(i=0;i<n;i++) { int xi, yi; xi=(int)set[i].x; yi=(int)set[i].y; g.drawRect(xi, yi,1,1); } g.drawString("INF311!", 50, 60 ); } }
- 49. 49 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Java applets <APPLET code = "AppletINF311.class" width = "500" height = "300" > </APPLET>
- 50. 50 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Java applets for online demos... Two technologies in use: ● Image segmentation ● Texture synthesis (hole filling) Try it !!! http://www.sonycsl.co.jp/person/nielsen/ClickRemoval/ F. Nielsen, R. Nock ClickRemoval: interactive pinpoint image object removal. ACM Multimedia 2005 Hallucination (mirage)
- 51. 51 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen There is much more in Java! JDKTM 6 Documentation
- 52. 52 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen A glimpse at object inheritance All objects inherit from the topmost object: Object ...meaning some methods are already predefined Can overwrite the method toString
- 53. 53 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen A glimpse at object inheritance Object public String toString() (superclass) Point2D public String toString() class Point2D {double x,y; // Constructor Point2D(double xi, double yi) {this.x=xi;this.y=yi; } // Overrides default method public String toString() {return "["+x+" "+y+"]"; } } class SuperClass { public static void main(String [] a) { Point2D myPoint=new Point2D(Math.PI, Math.E); System.out.println("Point:"+myPoint); } }
- 54. 54 A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen





![6
A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen
class MergeList
{
//
// Merge two ordered lists
//
static List mergeRec(List u, List v)
{
if (u==null) return v;
if (v==null) return u;
if (u.container < v.container)
{
// Recycle cells/ no new
u.next=mergeRec(u.next,v);
return u;
}
else
{
// Recycle cells/no new
v.next=mergeRec(u,v.next);
return v;
}
}
public static void main(String [] args)
{
List u=new List(8,null);
u=u.insert(6);u=u.insert(3);
u.Display();
List v=new List(9,null);
v=v.insert(7);v=v.insert(5);
v=v.insert(4);v=v.insert(2);
v.Display();
List w=mergeRec(u,v);
w.Display();
}](https://image.slidesharecdn.com/programmingalgorithmsjava-9-140701005620-phpapp01/85/chapter-9-A-Concise-and-Practical-Introduction-to-Programming-Algorithms-in-Java-6-320.jpg)

![8
A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen
public static void main(String [] args)
{
List u=new List(3,null);
u=u.insert(2);
u=u.insert(9);
u=u.insert(6);u=u.insert(1);
u=u.insert(15);u=u.insert(17);
u=u.insert(23);u=u.insert(21);
u=u.insert(19);u=u.insert(20);
u.Display();
List sortu=sortRec(u);
System.out.println("Sorted linked list:");
sortu.Display();
}
20-->19-->21-->23-->17-->15-->1-->6-->9-->2-->3-->null
Sorted linked list:
1-->2-->3-->6-->9-->15-->17-->19-->20-->21-->23-->null](https://image.slidesharecdn.com/programmingalgorithmsjava-9-140701005620-phpapp01/85/chapter-9-A-Concise-and-Practical-Introduction-to-Programming-Algorithms-in-Java-8-320.jpg)


![11
A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen
Exhaustive search & Backtracking
Incrementally place queen i (0...7) on the first free column
If there is no more free columns left, then backtrack:
backtrack:
Consider the previous queen position and increment its
column position, etc., etc., etc.
... until we find a solution
(=reach a successful location for queen indexed 7)
queen: 1D Array that specifies the column position
Queen i is located at position (i,queen[i])
(with i ranging from 0 to 7)
search: Static function that returns a/all solution(s).](https://image.slidesharecdn.com/programmingalgorithmsjava-9-140701005620-phpapp01/85/chapter-9-A-Concise-and-Practical-Introduction-to-Programming-Algorithms-in-Java-11-320.jpg)
![12
A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen
// Are queen (i1,j1) and queen (i2,j2) safe ?
static boolean WrongPos(int i1, int j1, int i2, int j2)
{ // same row?, same col?, same diag?
return (i1==i2 ||
j1==j2 ||
Math.abs(i1-i2) == Math.abs(j1-j2));
}
// Place safely queen i at column j?
static boolean FreeMove(int i, int j)
{
boolean result=true;
for(int k=0;k<i;k++)
result=result&&!WrongPos(i,j,k,queen[k]);
return result;
}
Check for the queens
placed so far
on the chessboard
Static functions to check for collisions](https://image.slidesharecdn.com/programmingalgorithmsjava-9-140701005620-phpapp01/85/chapter-9-A-Concise-and-Practical-Introduction-to-Programming-Algorithms-in-Java-12-320.jpg)
![13
A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen
static boolean search(int row)
{
boolean result=false;
if (row==n)
{// Terminal case
DisplayChessboard();
nbsol++;
}
else
{// Exhaustive search
int j=0;
while(!result && j<n)
{
if (FreeMove(row,j))
{
queen[row]=j;
result=search(row+1); // RECURSION/BACKTRACK
}
j++; // explore all columns
}
}
return result;
}
Increment the number
of found solutions
(static class variable)](https://image.slidesharecdn.com/programmingalgorithmsjava-9-140701005620-phpapp01/85/chapter-9-A-Concise-and-Practical-Introduction-to-Programming-Algorithms-in-Java-13-320.jpg)
![14
A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen
public static void main(String [] arguments)
{
nbsol=0;
search(0); // Call exhaustive search procedure
System.out.println("Total number of solutions:"+nbsol);
}
static final int n=8;
static int [] queen=new int[n];
static int nbsol;
static void DisplayChessboard()
{
int i,j;
System.out.println("");
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
{
if (queen[i]!=j) System.out.print("0");
else System.out.print("1");
}
System.out.println("");
}
}](https://image.slidesharecdn.com/programmingalgorithmsjava-9-140701005620-phpapp01/85/chapter-9-A-Concise-and-Practical-Introduction-to-Programming-Algorithms-in-Java-14-320.jpg)




![21
A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen
class SetCover
{
int nbelements;
int nbsubsets;
boolean [][] incidenceMatrix;
//Constructor
SetCover(int nn, int mm)
{
this.nbelements=nn; this.nbsubsets=mm;
incidenceMatrix=new boolean[nbsubsets][nbelements];
for(int i=0;i<nbsubsets;i++)
for(int j=0;j<nbelements;j++)
incidenceMatrix[i][j]=false;
}
void SetSubsets(int [] [] array) // Set incidence matrix
{for(int j=0;j<array.length;j++)
{for(int i=0;i<array[j].length;i++)
incidenceMatrix[j][array[j][i]]=true;
}
}
}](https://image.slidesharecdn.com/programmingalgorithmsjava-9-140701005620-phpapp01/85/chapter-9-A-Concise-and-Practical-Introduction-to-Programming-Algorithms-in-Java-21-320.jpg)
![22
A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen
void Display()
{
for(int i=0;i<nbsubsets;i++){
for(int j=0;j<nbelements;j++)
if (incidenceMatrix[i][j]) System.out.print("1");
else System.out.print("0");
System.out.println("");
}
}
public static void main(String [] args)
{
int [][] subsets={{0,1,3},{2,3,4}, {0,2,5},{1,2,4},{3,4,5},{0,2}};
SetCover setcover=new SetCover(6,6);
setcover.SetSubsets(subsets);
System.out.println("Set cover problem:");
setcover.Display();
}](https://image.slidesharecdn.com/programmingalgorithmsjava-9-140701005620-phpapp01/85/chapter-9-A-Concise-and-Practical-Introduction-to-Programming-Algorithms-in-Java-22-320.jpg)
![23
A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen
static boolean [] GreedySCP(SetCover problem)
{
boolean [] result=new boolean[problem.nbsubsets];
int cover=0; int select;
for(int i=0;i<problem.nbsubsets;i++) // initially no subsets
result[i]=false;
while(cover!=problem.nbelements)
{
// Choose largest not-yet covered subset
select=problem.LargestSubset();
result[select]=true;
// Update covered matrix
cover+=problem.Cover(select);
// Update incidence matrix
problem.Update(select);
System.out.println("Selected "+select+" Number of covered
elements="+cover);
problem.Display();
}
return result;
}
Greedy algorithm](https://image.slidesharecdn.com/programmingalgorithmsjava-9-140701005620-phpapp01/85/chapter-9-A-Concise-and-Practical-Introduction-to-Programming-Algorithms-in-Java-23-320.jpg)
![24
A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen
// Number of covered element by subset i
int Cover(int i)
{
int nbEl=0;
for(int j=0;j<nbelements;j++)
if (incidenceMatrix[i][j]) ++nbEl;
return nbEl;
}
// Report the current largest subset
int LargestSubset()
{
int i, nbel, max, select;
max=-1;select=-1;
for(i=0;i<nbsubsets;i++)
{
nbel=Cover(i);
if (nbel>max) {max=nbel; select=i;}
}
return select;
}
Methods of class
SetCover](https://image.slidesharecdn.com/programmingalgorithmsjava-9-140701005620-phpapp01/85/chapter-9-A-Concise-and-Practical-Introduction-to-Programming-Algorithms-in-Java-24-320.jpg)
![25
A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen
Methods of class
SetCover
// Update the incidence matrix
void Update(int sel)
{
int i,j;
for(i=0;i<nbsubsets;i++)
{
if (i!=sel) //use sel below so don't modify it
{
for(j=0;j<nbelements;j++)
if (incidenceMatrix[sel][j])
incidenceMatrix[i][j]=false;
}
}
// Remove the chosen subset as well
for(j=0;j<nbelements;j++)
incidenceMatrix[sel][j]=false;
}](https://image.slidesharecdn.com/programmingalgorithmsjava-9-140701005620-phpapp01/85/chapter-9-A-Concise-and-Practical-Introduction-to-Programming-Algorithms-in-Java-25-320.jpg)
![26
A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen
public static void main(String [] args)
{
int [] [] subsets ={{0,1,3},{2,3,4},
{0,2,5},{1,2,4},
{3,4,5},{0,2}};
SetCover setcover=new SetCover(6,6);
setcover.SetSubsets(subsets);
System.out.println("Set cover problem:");
setcover.Display();
boolean [] solution=GreedySCP(setcover);
System.out.print("Solution:");
for(int i=0;i<setcover.nbsubsets;i++)
if (solution[i]) System.out.print(" "+i);
System.out.println("");
}
Set cover problem:
110100
001110
101001
011010
000111
101000
Selected 0 Number of covered elements=3
000000
001010
001001
001010
000011
001000
Selected 1 Number of covered elements=5
000000
000000
000001
000000
000001
000000
Selected 2 Number of covered elements=6
000000
000000
000000
000000
000000
000000
Solution: 0 1 2](https://image.slidesharecdn.com/programmingalgorithmsjava-9-140701005620-phpapp01/85/chapter-9-A-Concise-and-Practical-Introduction-to-Programming-Algorithms-in-Java-26-320.jpg)

![28
A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen
int [] [] subsets={{0,1,2,3,4,5,6},{7,8,9,10,11,12,13},
{0,7},{1,2,8,9},{3,4,5,6,10,11,12,13}};
SetCover setcover=new SetCover(14,5);
Set cover problem:
11111110000000
00000001111111
10000001000000
01100000110000
00011110001111
Selected 4 Number of covered elements=8
11100000000000
00000001110000
10000001000000
01100000110000
00000000000000
Selected 3 Number of covered elements=12
10000000000000
00000001000000
10000001000000
00000000000000
00000000000000
Selected 2 Number of covered elements=14
00000000000000
00000000000000
00000000000000
00000000000000
00000000000000
Solution: 2 3 4
Etc...
Easy to build generic examples
where greedy does not behave well
with O(log n) approximation ratio](https://image.slidesharecdn.com/programmingalgorithmsjava-9-140701005620-phpapp01/85/chapter-9-A-Concise-and-Practical-Introduction-to-Programming-Algorithms-in-Java-28-320.jpg)


![31
A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen
Enumerating: A recursive approach
static void Display(boolean [] tab)
{
for(int i=0;i<tab.length;i++)
if (tab[i]) System.out.print("1 ");
else
System.out.print("0 ");
System.out.println("");
}
static void Enumerate(boolean [] selection, int pos)
{
if (pos==selection.length-1)
Display(selection);
else
{
pos++;
selection[pos]=true;
Enumerate(selection,pos);
selection[pos]=false;
Enumerate(selection,pos);
}
}
public static void main(String[] args)
{
int n=4;
int i;
boolean [] select=new boolean[n];
for(i=0;i<n;i++)
select[i]=false;
Enumerate(select,-1);
}](https://image.slidesharecdn.com/programmingalgorithmsjava-9-140701005620-phpapp01/85/chapter-9-A-Concise-and-Practical-Introduction-to-Programming-Algorithms-in-Java-31-320.jpg)
![32
A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen
Fully filling the knapsack
static void SolveKnapSack(boolean [] chosen, int goal, int
i, int total)
{
numbercall++; // keep track of total number of calls
if ((i>=chosen.length)&&(total!=goal)) return;
if (total==goal)
{ Display(chosen, goal);
numbersol++; // total number of solutions
}
else
{
chosen[i]=true;// add item first
SolveKnapSack(chosen,goal,i+1,total+weight[i]);
chosen[i]=false; // and then remove it
SolveKnapSack(chosen,goal,i+1,total);
}
}
final static int n=10; // 10 objects
static int [] weight={2,3,5,7,9,11,4,13,23,27};](https://image.slidesharecdn.com/programmingalgorithmsjava-9-140701005620-phpapp01/85/chapter-9-A-Concise-and-Practical-Introduction-to-Programming-Algorithms-in-Java-32-320.jpg)
![33
A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen
final static int n=10; // 10 objects
static int [] weight={2,3,5,7,9,11,4,13,23,27};
public static void main(String [] args)
{
int totalweight=51;
numbersol=0;
numbercall=0;
System.out.println("Knapsack:");
boolean [] chosen=new boolean[n];
SolveKnapSack(chosen, totalweight, 0, 0);
System.out.println("Total number of
solutions:"+numbersol);
System.out.println(" #calls="+numbercall);
}
Knapsack:
2+3+5+7+11+23+0=51
2+5+7+9+11+4+13+0=51
2+5+4+13+27+0=51
2+7+11+4+27+0=51
2+9+4+13+23+0=51
2+9+13+27+0=51
3+5+7+9+4+23+0=51
3+5+7+9+27+0=51
3+5+7+13+23+0=51
3+5+9+11+23+0=51
7+4+13+27+0=51
9+11+4+27+0=51
11+4+13+23+0=51
11+13+27+0=51
Total number of solutions:14
#calls=2029](https://image.slidesharecdn.com/programmingalgorithmsjava-9-140701005620-phpapp01/85/chapter-9-A-Concise-and-Practical-Introduction-to-Programming-Algorithms-in-Java-33-320.jpg)
![34
A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen
Exhaustive search: Branch & bound
static void SolveKnapSack(boolean [] chosen, int goal, int i,
int total)
{
numbercall++;
if (total>goal) return; // cut
if ((i>=chosen.length)&&(total!=goal)) return;
if (total==goal)
{ Display(chosen, goal);
numbersol++;
}
else
{
chosen[i]=true;// add item first
SolveKnapSack(chosen,goal,i+1,total+weight[i]);
chosen[i]=false; // and then remove it
SolveKnapSack(chosen,goal,i+1,total);
}
}
Stop recursion if we already
exceed the weight amount](https://image.slidesharecdn.com/programmingalgorithmsjava-9-140701005620-phpapp01/85/chapter-9-A-Concise-and-Practical-Introduction-to-Programming-Algorithms-in-Java-34-320.jpg)






![42
A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen
static int nbObjects=8;
static int [] weight={2,3,5,2,4,6,3,1};
static int [] utility={5,8,14,6,13,17,10,4};
static int weightmax=12;
static int [] [] array;
static void SolveDP()
{
int i,j;
array=new int[nbObjects][weightmax+1];
// initialize the first row
for(j=0;j<=weightmax;j++)
if (j<weight[0]) array[0][j]=0;
else array[0][j]=utility[0];
// for all other rows
for(i=1;i<nbObjects;i++)
{
for(j=0;j<=weightmax;j++)
if (j-weight[i]<0) array[i][j]=array[i-1][j];
else
array[i][j]=max( array[i-1][j],
array[i-1][j-weight[i]]+utility[i]);
}
}](https://image.slidesharecdn.com/programmingalgorithmsjava-9-140701005620-phpapp01/85/chapter-9-A-Concise-and-Practical-Introduction-to-Programming-Algorithms-in-Java-42-320.jpg)
![43
A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen
static void InterpretArray()
{
int i,u,w;
u=0;
w=weightmax;
for(i=nbObjects-1;i>=1;i--)
{
if (array[i][w]!=array[i-1][w])
{System.out.print((i+1)+" ");
w=w-weight[i];
u=u+utility[i];
}
}
if (array[0][w]!=0);
{System.out.println("1");
w=w-weight[0];
u=u+utility[0];
}
System.out.println("Cross check:"+u+" remaining weight "+w);
}](https://image.slidesharecdn.com/programmingalgorithmsjava-9-140701005620-phpapp01/85/chapter-9-A-Concise-and-Practical-Introduction-to-Programming-Algorithms-in-Java-43-320.jpg)
![44
A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen
public static void main(String[] args)
{
System.out.println("Solving knapsack using the dynamic
programming paradigm.");
SolveDP();
Display();
System.out.println("Reading solution:");
InterpretArray();
}](https://image.slidesharecdn.com/programmingalgorithmsjava-9-140701005620-phpapp01/85/chapter-9-A-Concise-and-Practical-Introduction-to-Programming-Algorithms-in-Java-44-320.jpg)



![48
A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen
import java.awt.*;
import java.applet.*;
class Point2D
{double x,y;
Point2D()
{this.x=300.0*Math.random();
this.y=300.0*Math.random();}}
public class AppletINF311 extends Applet {
final static int n=100;
static Point2D [] set;
public void init() {
int i;
set=new Point2D[n];
for(i=0;i<n;i++)
set[i]=new Point2D();}
public void paint(Graphics g) {int i;
for(i=0;i<n;i++)
{
int xi, yi;
xi=(int)set[i].x; yi=(int)set[i].y;
g.drawRect(xi, yi,1,1);
}
g.drawString("INF311!", 50, 60 );
}
}](https://image.slidesharecdn.com/programmingalgorithmsjava-9-140701005620-phpapp01/85/chapter-9-A-Concise-and-Practical-Introduction-to-Programming-Algorithms-in-Java-48-320.jpg)




![53
A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen
A glimpse at object inheritance
Object
public String toString()
(superclass)
Point2D
public String toString()
class Point2D
{double x,y;
// Constructor
Point2D(double xi, double yi)
{this.x=xi;this.y=yi; }
// Overrides default method
public String toString()
{return "["+x+" "+y+"]"; }
}
class SuperClass
{
public static void main(String [] a)
{
Point2D myPoint=new Point2D(Math.PI, Math.E);
System.out.println("Point:"+myPoint);
}
}](https://image.slidesharecdn.com/programmingalgorithmsjava-9-140701005620-phpapp01/85/chapter-9-A-Concise-and-Practical-Introduction-to-Programming-Algorithms-in-Java-53-320.jpg)
